Как подготовиться к ЕГЭ по математике

Подготовка к ЕГЭ по математике

Из каких частей состоит ЕГЭ по математике в 2025 году

Математика — один из двух обязательных предметов на ЕГЭ. Но, в отличие от русского языка, эта дисциплина предлагает 2 уровня сложности: профильный и базовый. Какой именно вариант выбрать, зависит от вашей цели. Если вуз, в который вы хотите поступить, требует профильного уровня, нужно сдавать его. Обычно это касается технических специальностей.

Для получения аттестата выпускникам школ хватит и базового. Но финальное решение за вами. Если вы хотите сдать профильный вариант, просто чтобы проверить свои знания и уровень подготовки, — дерзайте!

Структура базового уровня ЕГЭ по математике

Базовый уровень проверяет основные знания школьника по математике. Такой экзамен не делится на части: в него входит только 21 задание с кратким ответом. Ответом может быть целое число, десятичная дробь или ряд цифр. По уровням сложности задания экзамена тоже не делятся — все задачи в нем базового уровня. Чтобы выполнить такую работу, ученику дают 180 минут.

Изменений по сравнению с 2024 годом в базовом уровне нет.

Структура профильного уровня ЕГЭ по математике

Варианты профильного уровня проверяют основные и углубленные знания школьника. В 2025 году ЕГЭ состоит из 2 частей:

• 1-я часть: 12 задач с кратким ответом;

• 2-я часть: 7 задач с развернутым ответом.

В первой части ответом может быть целое число, десятичная дробь или ряд цифр. Во второй части — полное обоснованное решение и ответ. Чтобы выполнить задания экзамена, школьнику дают 235 минут.

Задачи ЕГЭ по математике профильного варианта делятся на категории по уровням сложности. В таблице ниже можно увидеть, как именно.

Базовый	7
Повышенный	10
Высокий	2
Всего	19

Изменений по сравнению с 2024 годом в профильном уровне также нет.

Как сдать ЕГЭ по математике: разбор сложных задач

Экзамен по математике не зря считают одним из самых трудных. Даже в заданиях базового варианта можно легко ошибиться по невнимательности. Что уж говорить о действительно сложных задачах с полным решением, где много «подводных камней»? Чтобы вы знали, как подготовиться к ЕГЭ по профильной математике, мы разобрали несколько из них.

Задание 17

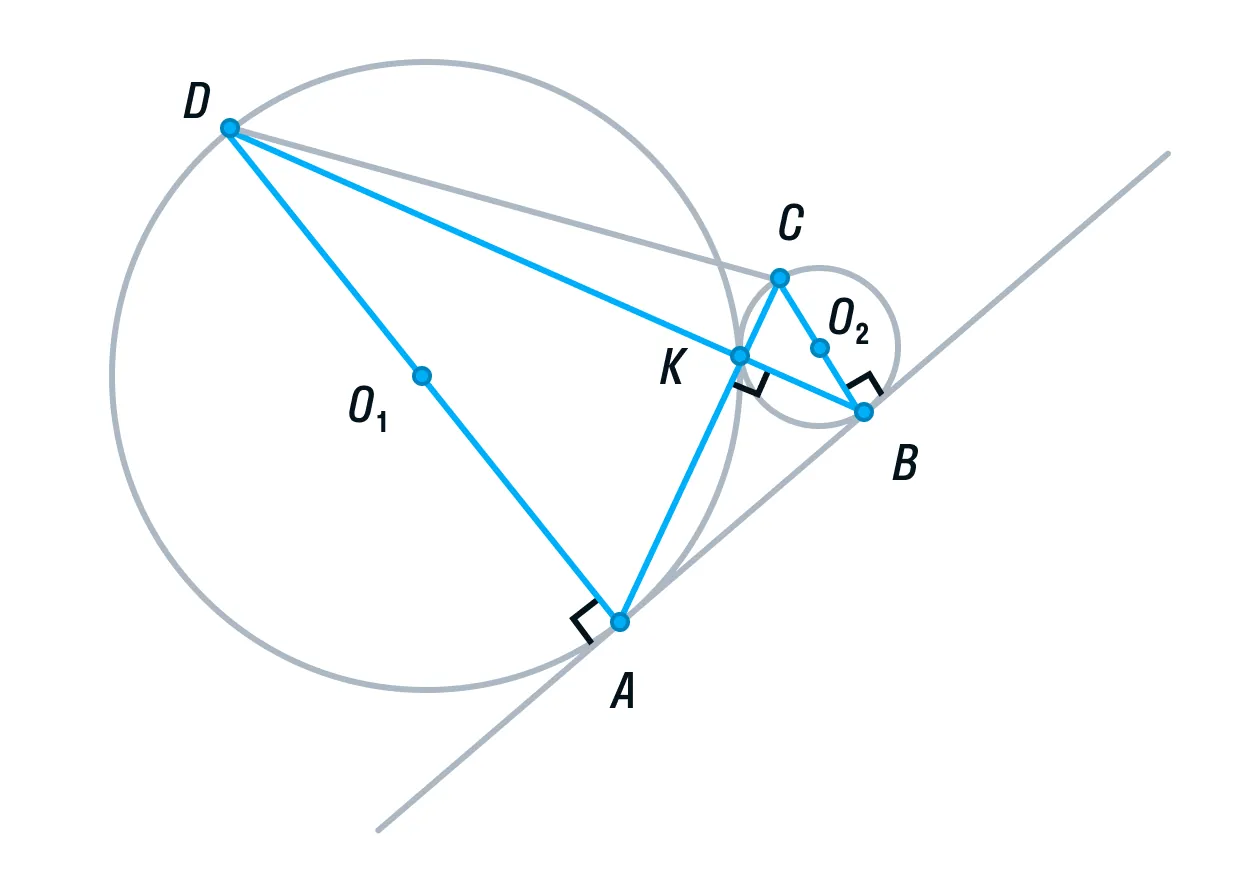
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.

а) Докажите, что прямые AD и BC параллельны.

б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.

Совет

Для этого задания советуем повторить темы:

• Касательные к окружности и их свойства.

• Свойства вписанных углов.

• Взаимное расположение окружностей.

• Свойства прямоугольного треугольника.

• Признаки и свойства параллельных прямых.

• Подобные треугольники, площади подобных фигур.

• Свойство площадей (в частности: отношение площадей треугольников с одинаковой стороной).

• Трапеция, её свойства. Площадь трапеции.

• Теорема Пифагора.

Проследите, чтобы они были в вашем плане подготовки к профилю ЕГЭ по математике.

Решение

а) Выполним построение.

1. Окружности с центрами О₁ и О₂ соответственно касаются друг друга в одной точке К.

2. Прямая АВ касается обеих окружностей в точках А и В соответственно.

3. Прямые АК и ВК пересекают окружности в точках С и D соответственно

4. Пусть общая касательная окружностей в точке К, пересекает прямую АВ в точке М.

   

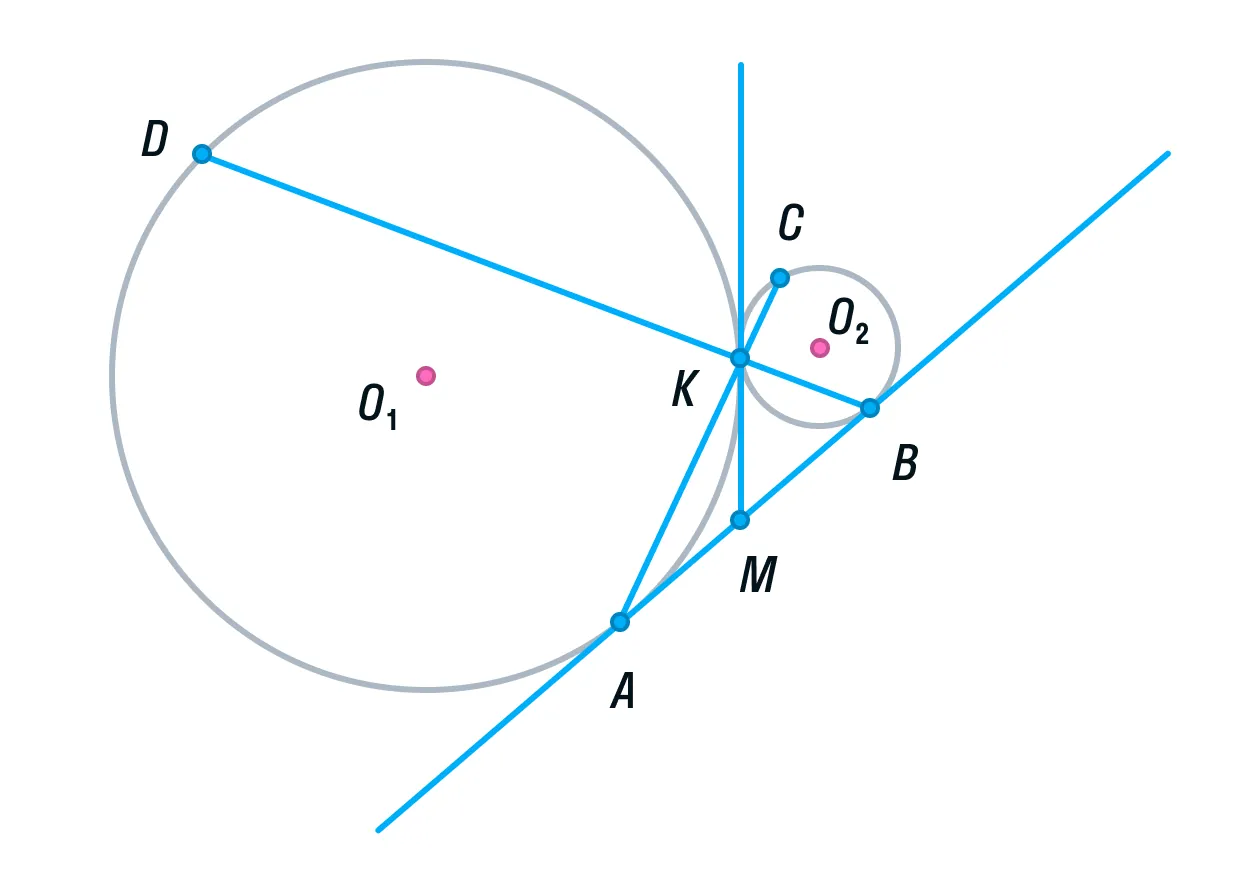
   Тогда по свойству касательных, проведенных из одной точки, AM = KM и KM = BM.

   

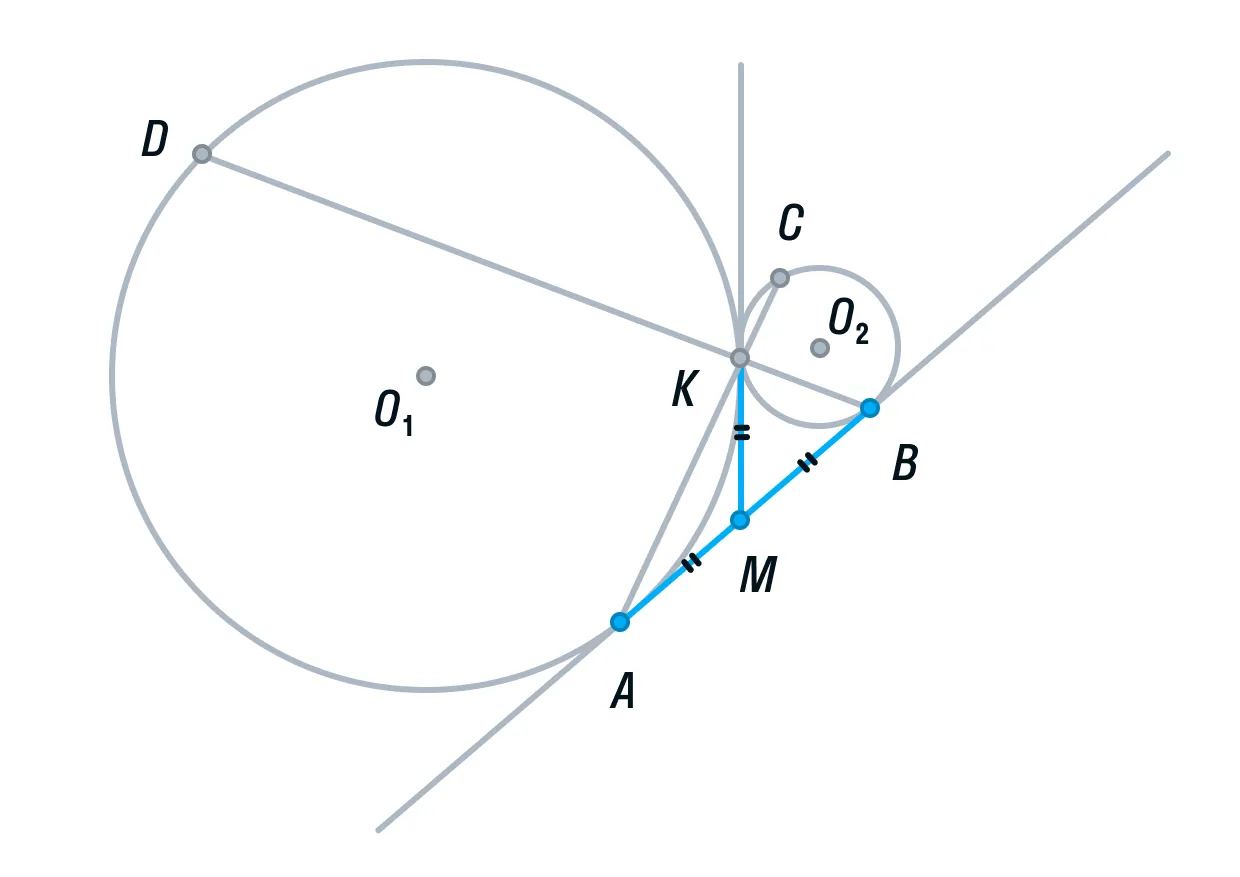
5. Рассмотрим треугольник АВК. Его медиана АМ равна половине стороны, которую она разбивает. Следовательно, делаем вывод, что треугольник АВК прямоугольный, а угол К = 90°.

   

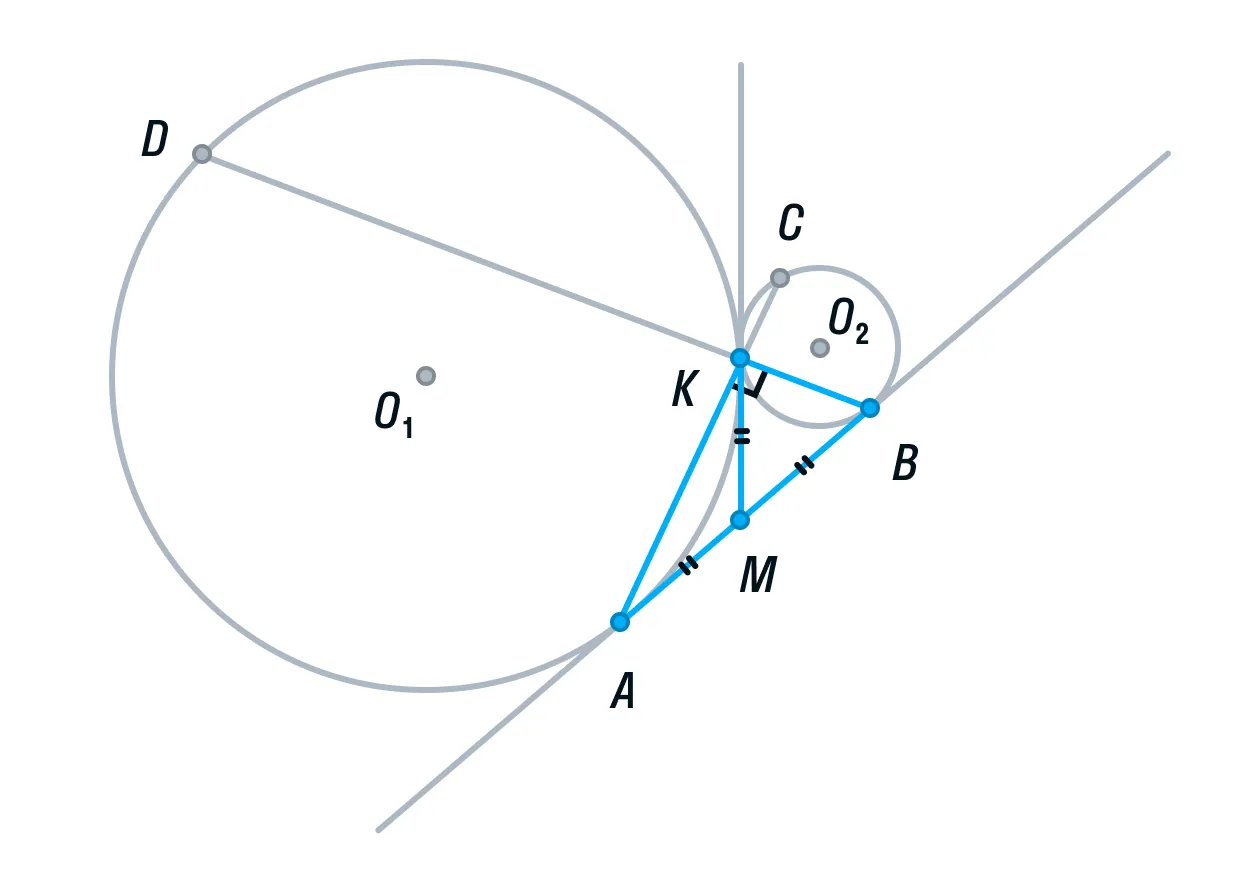
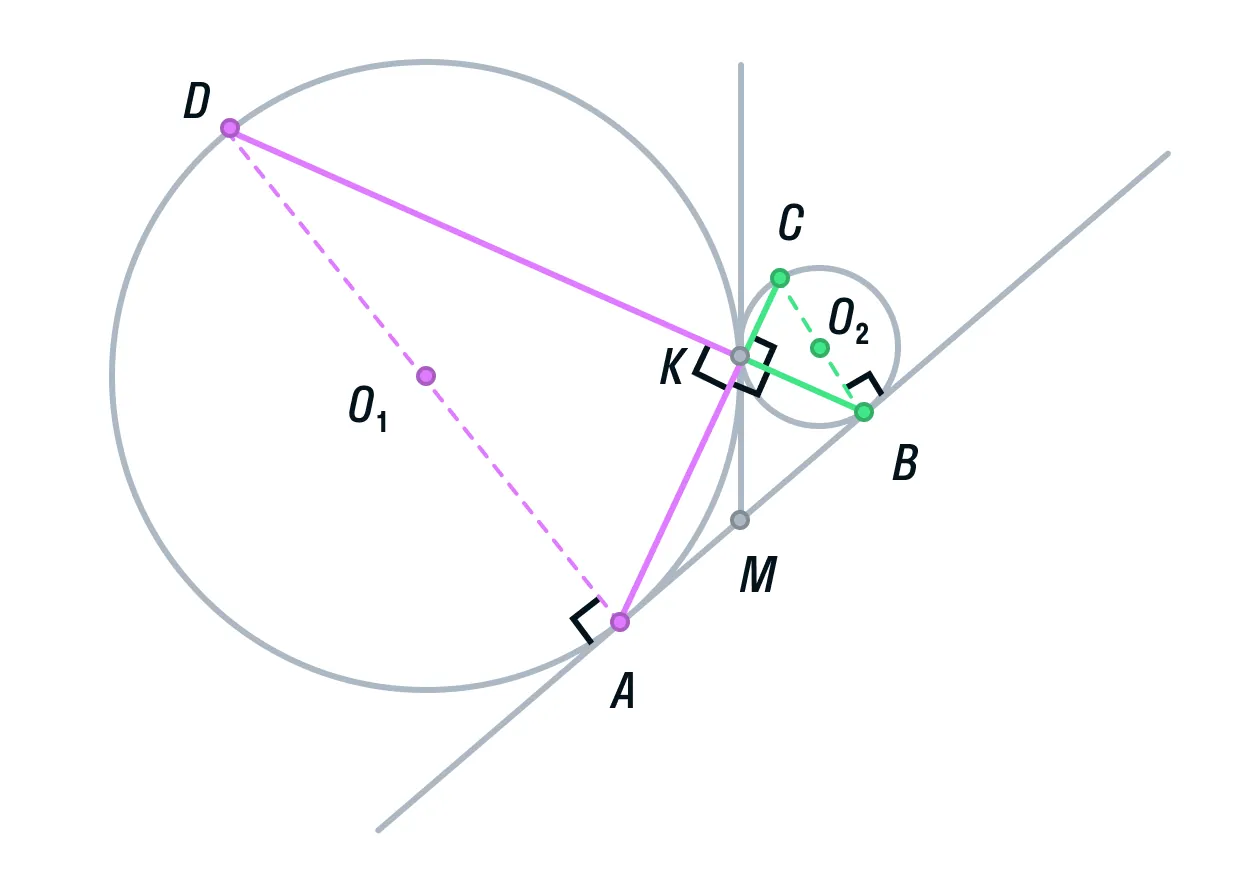
6. Вписанный угол AKD является смежным углом АКВ, а значит, он тоже 90° как прямой. Следовательно, угол AKD опирается на диаметр AD. Значит, AD ⊥ AB, так как радиус, а в данном случае диаметр, перпендикулярен касательной в точке касания.

7. Аналогично рассмотрев угол ВКС, получим, что BC⊥ AB.

   

8. Прямые AD и ВС перпендикулярны третьей прямой АВ, следовательно, прямые AD и BC параллельны. Ч. т. д.

б) Пусть радиус первой окружности равен 4, а радиус второй окружности равен 1. Тогда АD = 8, ВС = 2.

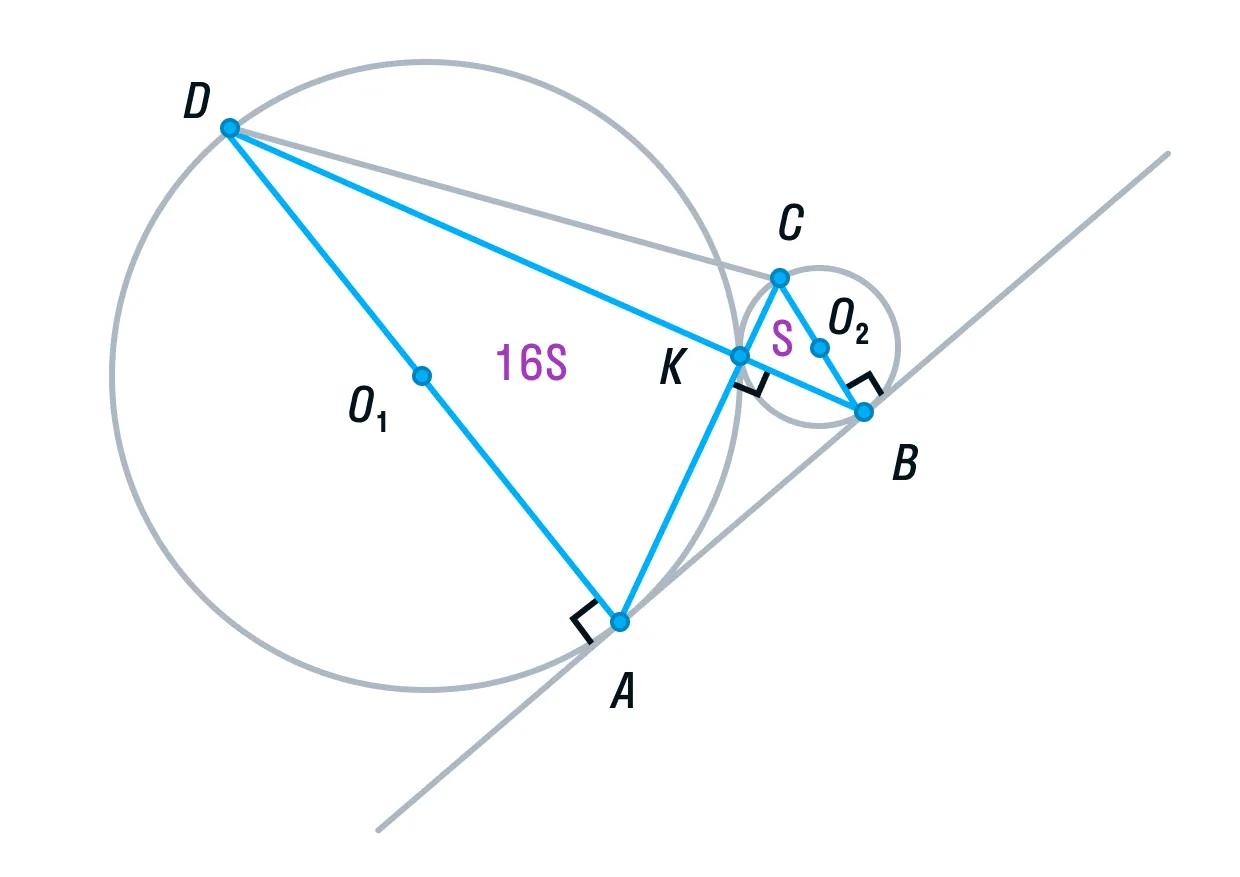
1. Рассмотрим треугольники ADK и СВК. Они подобны, т. к. имеют два равных угла (К – вертикальный, С и А — накрест лежащие). Из подобия треугольников следует, что их площади относятся как коэффициент подобия в квадрате:

2. Обозначим площадь треугольника СВК за S, тогда площадь треугольника ADK будет равна 16S.

   

3. Пусть площади треугольников АВК и CDK будут равны х и у соответственно.

   

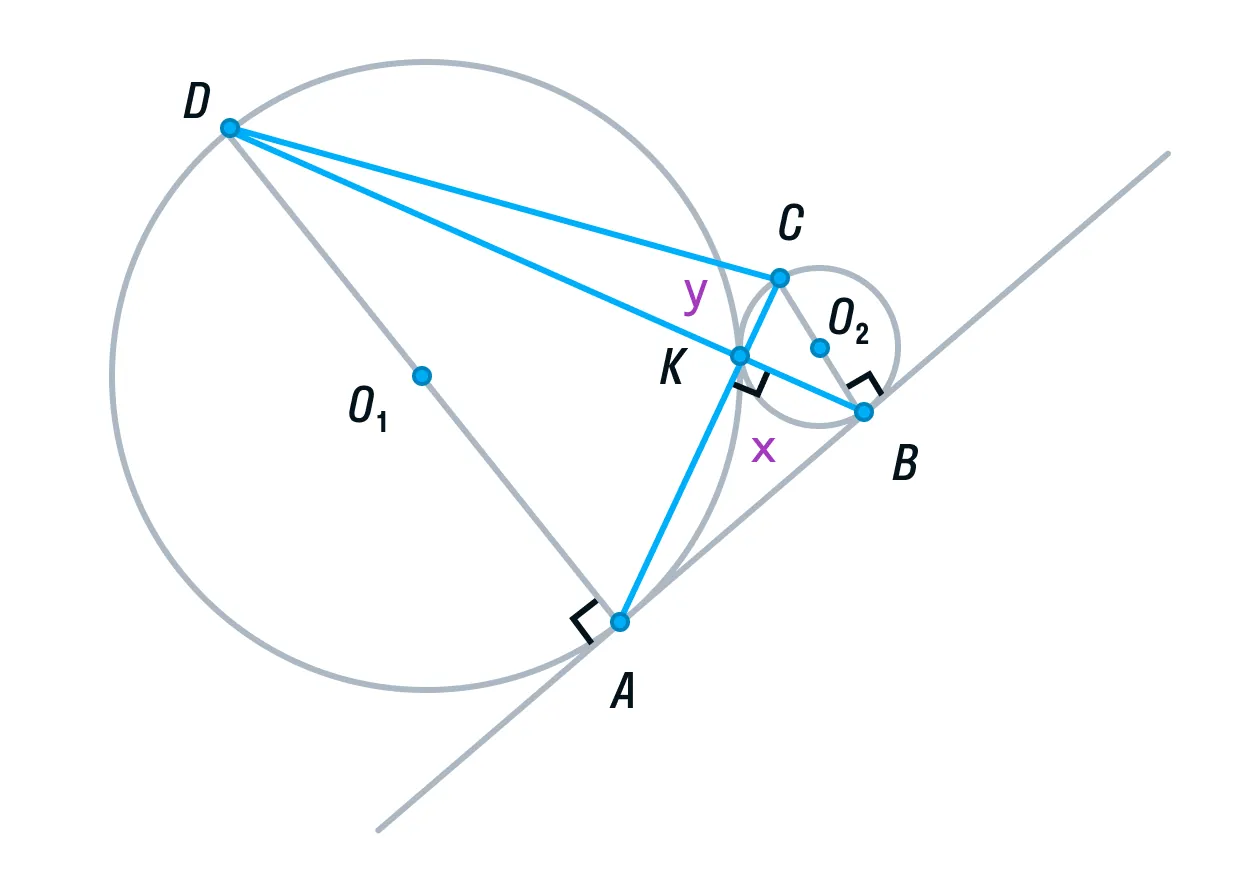
4. Вспомним свойство, связывающее высоты треугольников с общим основанием и получим следующие равенства: DB — общая сторона треугольников ADB и СDB, следовательно:

   (равно 4 из подобия треугольников ADK и СВК, см. выше),

   

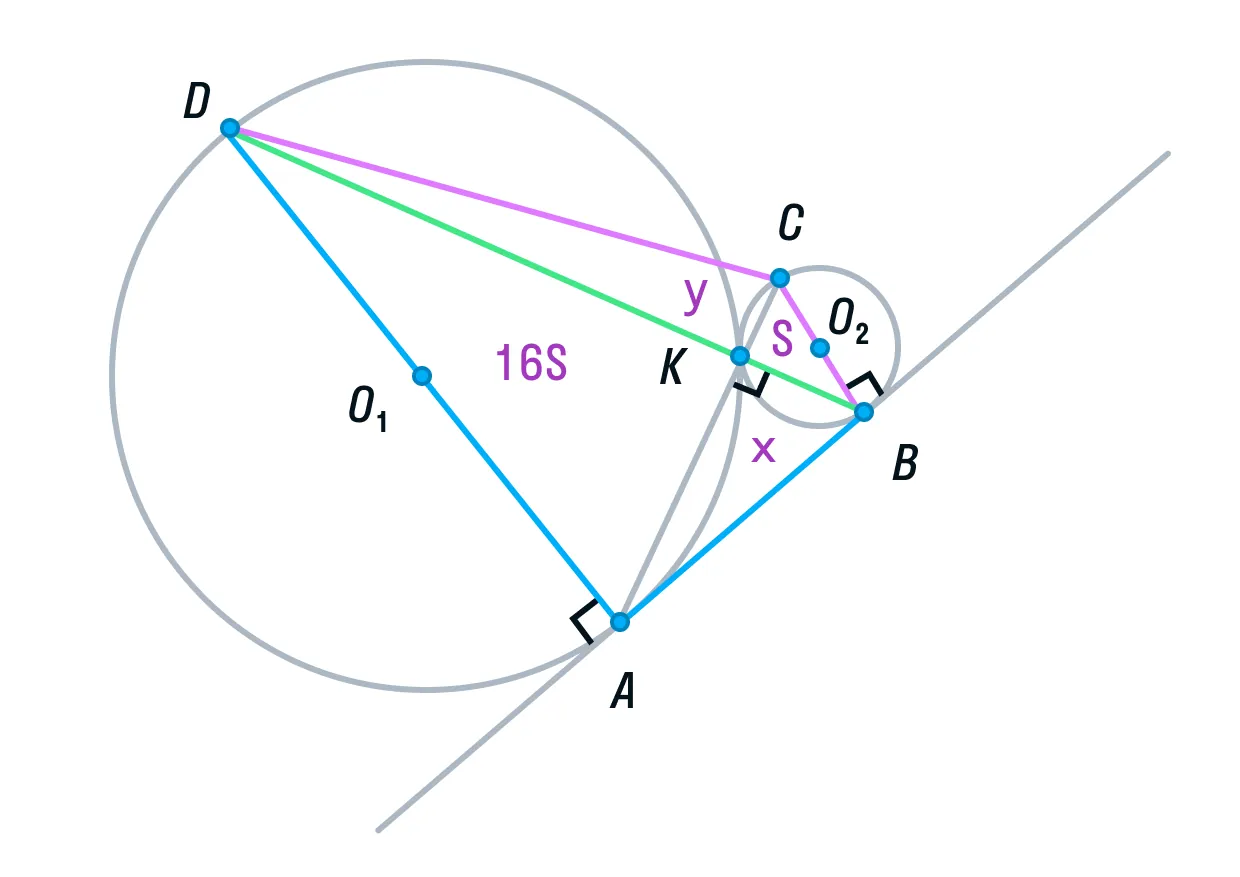
5. Аналогично, AC — общая сторона треугольников ADС и ABC, следовательно,

   (равно 4 из подобия треугольников ADK и СВК, см. выше),

   

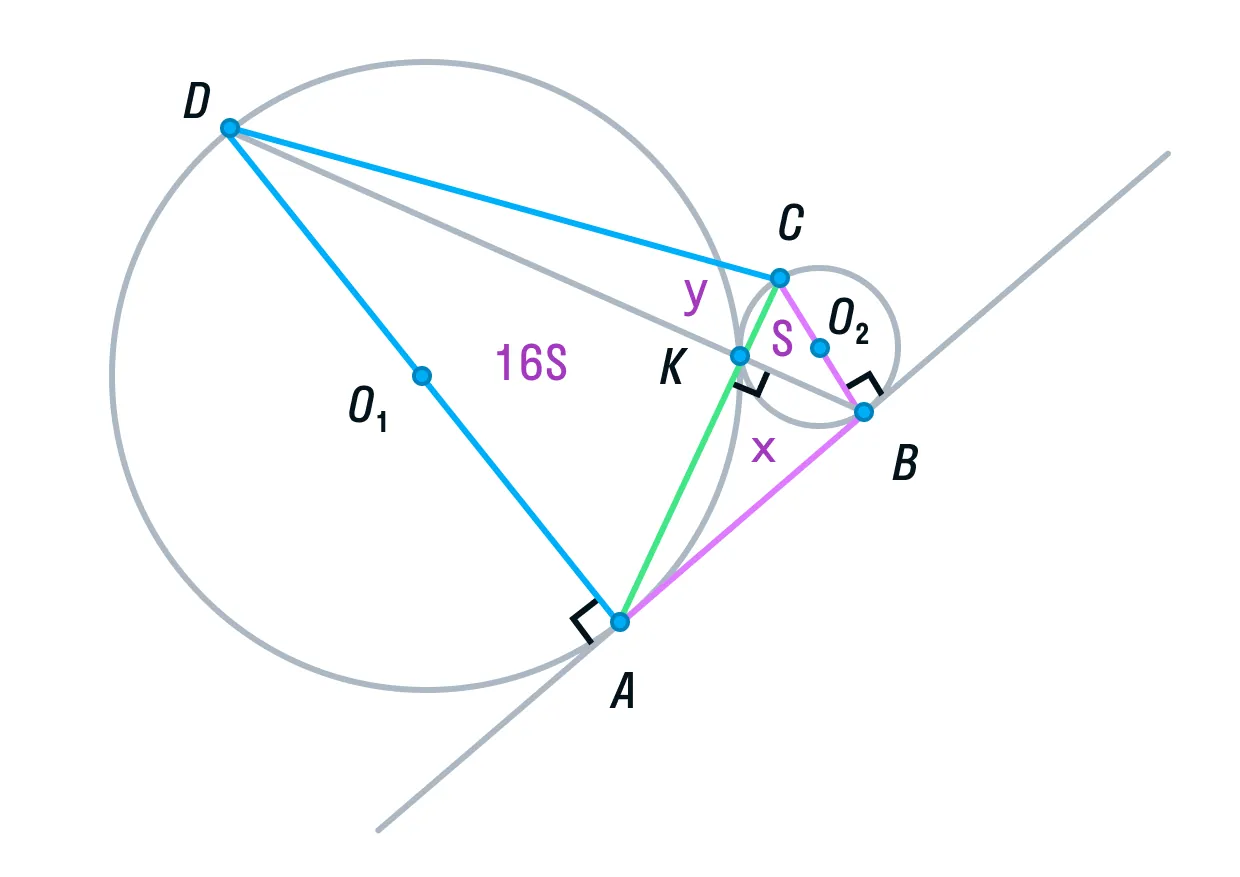
6. Решим полученную систему уравнений:

7. Из первого уравнения подставим во второе и найдем y.

   следовательно, подставим во второе и найдем y.

8. Площадь ABCD равна 16S + 4S + 4S + S = 25S.

9. Заметим, что ABCD — прямоугольная трапеция (AD||BC, AB — перпендикулярна основаниям). Для вычисления ее площади нужно полусумму оснований умножить на высоту.

   

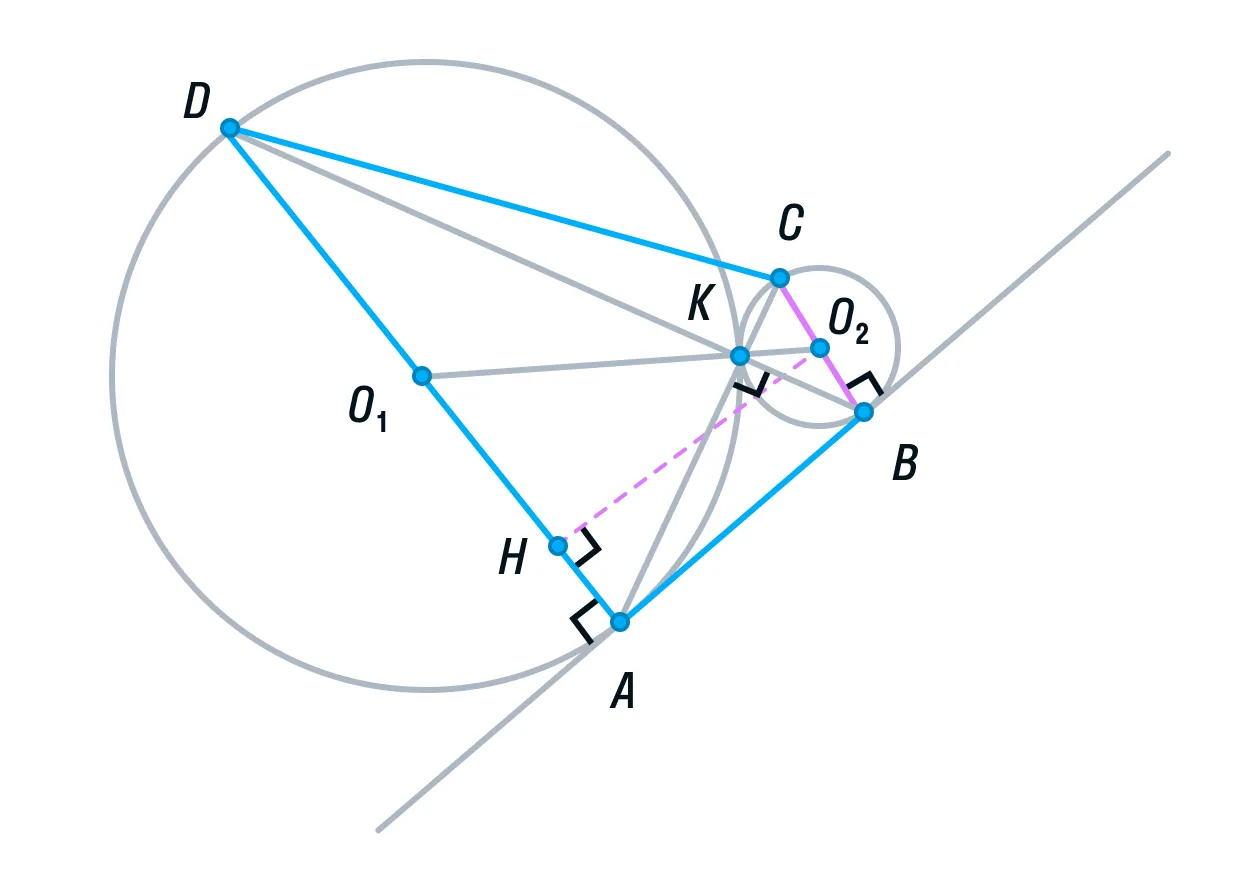
10. Для того, чтобы найти высоту, рассмотрим меньшую трапецию AO₁O₂B.

    

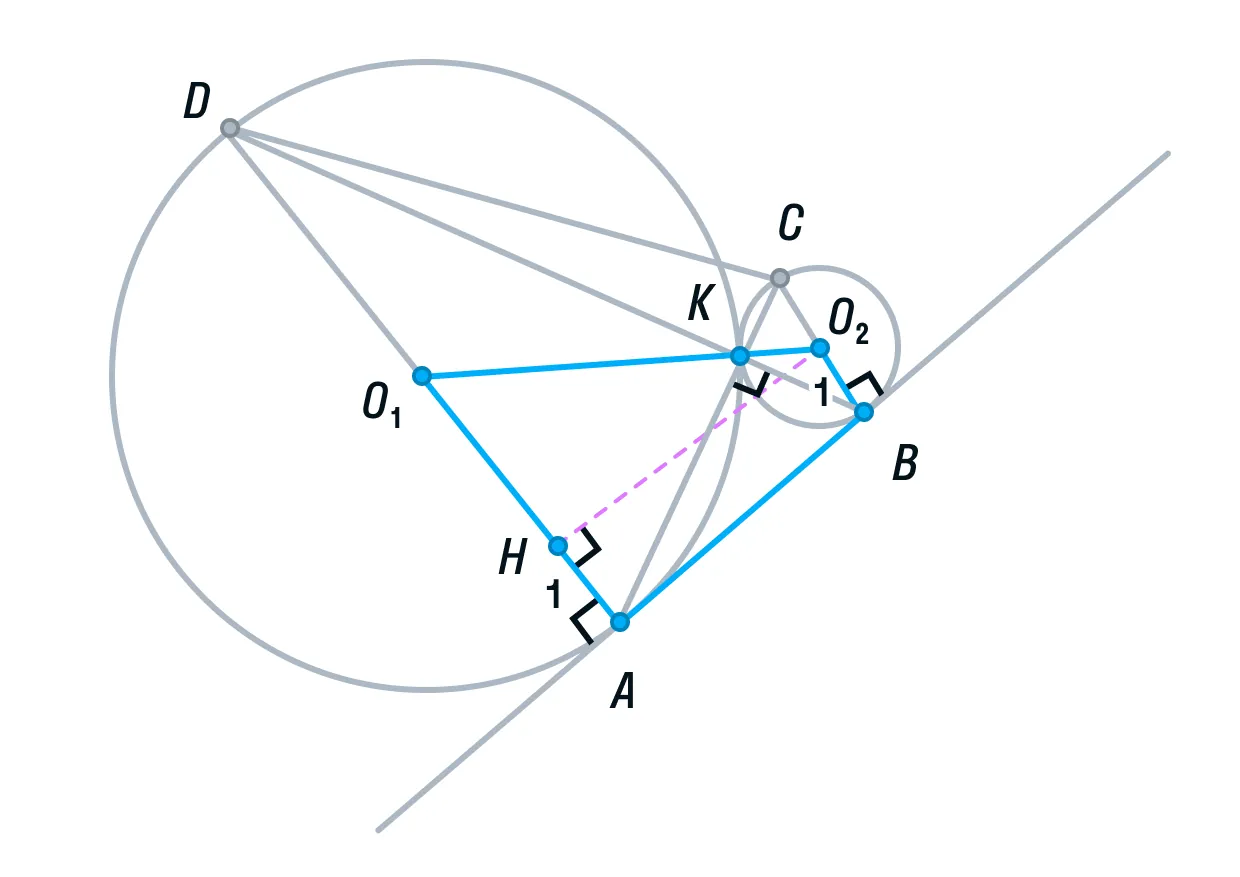
    Ее основания равны 1 и 4, так как О₂В и О₁А — радиусы. O₁O₂ = 5, так как О₂К и О₁К — радиусы. О₂H — высота трапеции AO₁O₂B.

11. По теореме Пифагора найдём О₂H:

12. Вычислим площадь трапеции ABCD:

13. С другой стороны мы нашли Отсюда S = 0,8.

14. Площадь треугольника АКВ = 4S, следовательно,

Ответ: 3,2.

Задание 19

В школах № 1 и № 2 учащиеся писали тест. В каждой школе тест писали по крайней мере 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешел из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.

а) Мог ли средний балл в школе № 1 уменьшиться в 10 раз?

б) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 7?

в) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.

Совет

Чтобы справиться с этой задачей, нужно повторить темы:

• Понятие натурального и целого числа.

• Среднее арифметическое.

• Делимость чисел.

• Процент. Нахождение процента от числа, уменьшение числа на заданный процент.

• Составление и решение линейных уравнений.

Добавьте их в ваш план подготовки к ЕГЭ по математике, если собираетесь сдавать профиль.

Решение:

а)

1. Допустим, что в школе № 1 писали тест 2 учащихся, один из них набрал 1 балл, а второй набрал Х баллов и перешёл в другую школу. Тогда средний балл в школе был равен (1 + Х) : 2 = 10, а стал равен 1, т. е. уменьшился в 10 раз.

2. Решим уравнение и получим Х = 19 — натуральное число. Следовательно, наше предположение верно.

3. Или мы можем предположить другой вариант: что один учащийся набрал 2 балла. Тогда средний балл изначально равняется 20, а после ухода второго станет 2, т. е. изменится в 10 раз.

4. Решим уравнение (2 + Х) : 2 = 20, отсюда Х = 38 — натуральное число, что тоже удовлетворяет условию задачи.

Ответ: средний балл в школе № 1 мог уменьшиться в 10 раз.

б)

1. Пусть в школе № 2 писали тест m учащихся, n — сумма баллов m учащихся, средний балл равнялся B, а перешедший в неё учащийся набрал u баллов.

2. Умножим обе части полученного уравнения на 10, получим:

3. По условию B = 7, тогда получим, что 10u кратно 10, а не делится на 10, так как ни один из множителей не делится на 10. Это противоречие.

Ответ: Первоначальный средний балл в школе № 2 не мог равняться 7.

в)

1. Пусть в школе № 1 средний балл равнялся A, общее количество баллов — p, количество писавших работу — (9 – m).

   (из пункта б).

   Следовательно,

2. Попробуем найти средний балл в школе № 2 методом подбора. Пусть:

   В = 1, тогда:

   кратно 10, а не делится на 10.

   В = 2, тогда:

   пусть u = 1, тогда m = 4:

   — не является целым числом.

   u = 2 не может быть, т. к. m ≥ 1

   В = 3, тогда:

   кратно 10, а не делится на 10.

   В = 4, тогда:

   Чтобы m было натуральным числом u должно быть четным, u = 2, тогда m = 4, что невозможно (доказали при В = 2).

   u = 4, тогда m меньше 0, что невозможно т. к. m ≥ 1.

   В = 5, тогда:

   пусть u = 1, тогда m = 7, что невозможно (доказали в пункте б);

   пусть u = 2, тогда m = 5:

   — не является целым числом;

   пусть u = 3, тогда m = 3:

3. Этот случай реализуется, например, в школе № 2 при m = 3, B = 5. Предположим, что каждый ученик набрал по 5 баллов. Тогда в школе № 1 писали 9 – m = 9 – 3 = 6 учащихся, 3 из них набрали по 1 баллу, а 3 – по 3 балла, тогда средний балл:

4. Переход из школы № 1 в школу № 2 совершил ученик с 3 баллами, тогда средний балл в школе № 1 стал равен:

   что на 10% меньше от первоначального значения.

5. Тогда средний балл в школе № 2 стал равен:

   что на 10% меньше от первоначального значения.

Ответ: наименьшее значение первоначального среднего балла в школе № 2 равно 5.

Ответ: а) да; б) нет; в) 5.

170.4K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Как выставляют баллы за ЕГЭ по математике

С базовым уровнем сложности все просто: за каждый правильный ответ вашего варианта вы получаете по 1 первичному баллу. То же самое касается и первой части профиля: задания 1–12 тоже оценивают в 1 балл.

Как вы помните, во 2-й части профильного варианта нужны и решение, и ответ. Здесь задания оценивают по нескольким критериям. Они сложнее, но и баллов за них можно получить больше. Давайте же разберемся, как выставляют баллы во второй части профиля. Это поможет вам подготовиться к заданиям ЕГЭ по математике как самостоятельно, так и с учителем.

Задание № 13	Баллы
В обоих пунктах есть обоснованные ответы	2
Есть обоснованный ответ только в пункте а или есть неверный ответ из-за ошибки в вычислениях, но шаги в решениях обоих пунктов верные	1
Все остальные случаи	0
Максимальный балл	2

Задание № 14	Баллы
Верно доказан пункт а, в пункте б есть обоснованный ответ	3
Есть только обоснованный ответ в пункте б или верно доказан пункт а, в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ	2
Есть только верное доказательство пункта а, или в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ, или есть обоснованный ответ в пункте в, который получен с помощью пункта а, но сам пункт а не выполнен	1
Все остальные случаи.	0
Максимальный балл	3

Задание № 15	Баллы
Есть обоснованный ответ	2
Ответ обоснован, но он отличается от верного исключением точек –12 и/или 0 или шаги решения верные, но из-за ошибки в вычислениях получен неверный ответ	1
Все остальные случаи	0
Максимальный балл	2

Задание № 16	Баллы
Есть обоснованный ответ	2
Ученик верно построил математическую модель	1
Все остальные случаи	0
Максимальный балл	2

Задание № 17	Баллы
Верно доказан пункт а, в пункте б есть обоснованный ответ	3
Есть только обоснованный ответ в пункте б ИЛИ Верно доказан пункт а, в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ	2
Есть только верное доказательство пункта а, или в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ, или есть обоснованный ответ в пункте в, который получен с помощью пункта а, но сам пункт а не выполнен	1
Все остальные случаи	0
Максимальный балл	3

Задание № 18	Баллы
Есть обоснованный ответ	4
Рассуждения и значения параметра верные, но в ответе есть 1–2 неверных значения или решение недостаточно обосновано	3
Есть верное рассуждение и хотя бы одно правильное значение	2
Задача сведена к исследованию взаимного расположения 3 окружностей или двух квадратных уравнений с параметром	1
Все остальные случаи	0
Максимальный балл	4

Задание № 19	Баллы
Есть обоснованный ответ в пунктах а, б, в	4
Есть обоснованный ответ в пункте в и есть обоснованный ответ в пунктах а или б	3
Есть обоснованный ответ в пунктах а и б или есть обоснованный ответ в пункте в.	2
Есть обоснованный ответ в пунктах а или б	1
Все остальные случаи	0
Максимальный балл	4

Узнать больше о структуре экзамена, вариантах и критериях, по которым оценивают работы, можно на официальном сайте ФИПИ, в разделе «Демоверсии, спецификации, кодификаторы». Там же вы найдете методические указания для подготовки.

Сколько баллов нужно набрать, чтобы получить 3, 4 и 5

Теперь, когда мы разобрали критерии, можно посчитать, сколько баллов нужно набрать на конкретную оценку. В этом нам помогут таблицы ниже. Заодно разберемся, как первичные баллы переводятся в тестовые — финальные.

Шкала перевода баллов в базовой математике
Первичные баллы	Оценка
<7	2
7–11	3
12–16	4
17–21	5
Максимальный балл	4

Обратите внимание: с 2008 года официально баллы ЕГЭ не переводят в привычные нам оценки по пятибальной системе. Но если вам хочется это сделать, можно примерно оценить работу по таблице ниже.

Шкала перевода баллов в профильной математике (неофициальная)
Первичные баллы	Тестовые баллы	Оценка
<5	<27	2
5–8	27–49	3
8–20	50–67	4
21–31	68–100	5

6 советов от эксперта, как готовиться к ЕГЭ по математике

Мы занимаемся подготовкой учеников к экзамену каждый год и понимаем, насколько это важно и волнительно. Вам предстоит ответственная работа, от которой многое зависит. Чтобы облегчить ее, мы собрали несколько советов, которые помогут вам как можно лучше подготовиться к ЕГЭ по математике:

• Осознанно выберите уровень сложности и поставьте цель в баллах.

• Составьте план подготовки к ЕГЭ по математике: больше времени уделяйте темам, которые у вас «западают». Чтобы выявить их, ученики Skysmart проходят тест на бесплатном уроке.

• Узнайте все о ЕГЭ: сколько времени длится экзамен, из каких частей состоит, по каким темам будут задания, сколько вариантов, какие дадут справочные материалы и т. д.

• Составьте сбалансированное расписание для подготовки и следите, чтобы в нем было достаточно времени для отдыха.

• Много практикуйтесь: решайте пробные варианты ЕГЭ по базовой или профильной математике в бесплатном тренажёре ЕГЭ от Skysmart.

• Систематически консультируйтесь и занимайтесь с наставником, который часто имеет дело с подготовкой к ЕГЭ — преподавателем в школе или репетитором.

Все пункты в этом списке важны для тех, кто хочет набрать 80–100 баллов, но последний — особенно. Преподаватель расскажет о том, что представляет из себя ЕГЭ, и тогда на реальном экзамене не будет неприятных сюрпризов.

На курсах подготовки к ЕГЭ по математике в Skysmart учителя помогают школьникам разобраться в КИМах и прорешать каждый тип задач. Ученики заранее знакомятся с частыми ошибками, что помогает избегать их в работе и сохранять баллы. А еще мы учим готовиться морально, чтобы не допустить ошибок из-за паники и невнимательности. Начните подготовку к ЕГЭ по математике с нуля вместе со Skysmart: первый урок — бесплатно!