Вычисление первообразной функции

Практикуйся по этой теме! Пройди задание №8 ЕГЭ по профильной математике

Поговорим мы сегодня именно об этой прекрасной даме: узнаем, что такое первообразная, как она связана с интегралами и производными, и что самое важное, как её рассчитать без особого труда.

Дифференцирование и интегрирование

Если проанализировать все математические действия, то большинству из них будет соответствовать какое-то обратное:

• сложение обратно вычитанию,

• умножение — делению,

• возведение в степень — извлечению арифметического корня.

С производной то же самое: мы можем продифференцировать функцию, а можем произвести обратный процесс — интегрирование.

Дифференциация — операция взятия полной или частной производной функции.

Интегрирование — процесс поиска интеграла; восстановление функции по её производной.

Нахождение производной от функции обозначается знаком ′. Так, если исходная функция — y, то её производная будет обозначаться y′.

Чтобы взять производную от функции, мы воспользуемся таблицей производных и правилами дифференцирования.

Функция f (x)	Производная f' (х)
С (т. е. константа, любое число)	0
х	1
xn	nxn-1
√x	1/(2√x)
sin x	cos x
cos x	-sin x
tg x	1/cos2(х)
ctg x	-1/sin2x
ex	ex
ax	ax * ln a
ln x	1/x
logax	1/(x * ln a)

Правила дифференцирования

(c ⋅ f)′ = c ⋅ f′

(u + v)′ = u′ + v′

(u - v)′ = u′ - v′

(u ⋅ v)′ = u′v + v′u

(u/v)' = (u'v - v'u)/v²

u, v, f — это функции, а c — константа (любое число).

У интегрирования тоже есть своё обозначение — ∫. То есть если мы хотим взять интеграл от функции f(x), мы запишем это так: ∫f(x) dx.

Внимательные заметили в записи интегрирования непривычное для нас «dx». Что это такое? Зачем добавлять эти буквы в выражение для интеграла? Сейчас во всём разберёмся!

Дифференциал

Разберём буквы dx по отдельности:

• d — это дифференциал,

• х — функция, по которой будет произведено дифференцирование.

Так, если мы дифференцируем функции y, f, m, то их дифференциалы запишем соответственно как dy, df, dm.

Дифференциал в математике (от лат. differentia — разность, различие) — линейная часть приращения функции.

То есть это понятие родственно производной — но для чего его записывать рядом с интегралом?

Для понимания важности дифференциала в записи рассмотрим рисунок:

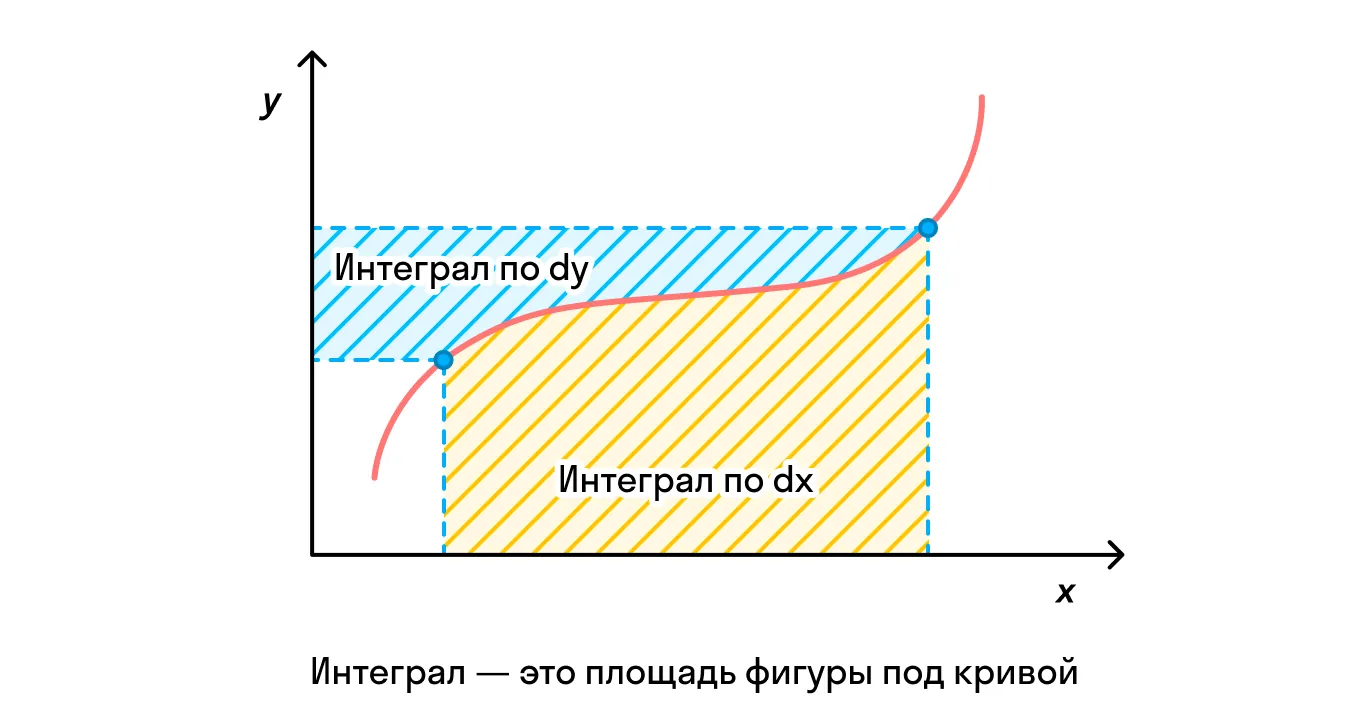
Геометрический смысл интеграла — это площадь фигуры под кривой функции. Если поместить график в декартову систему координат OХY, то эту площадь можно рассчитать относительно и оси ОХ, и оси ОУ, и именно дифференциал вносит ясность в выбор.

Понятие дифференциала в математике очень важное, глубокое, имеет множество нюансов использования, но сейчас нам важно понимать две вещи:

• дифференциал показывает, какую конкретно функцию мы будем интегрировать;

• его обязательно нужно записывать рядом с интегралом!

170.4K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Что такое первообразная?

Пришло время познакомиться с её величеством первообразной! Начнём с определения.

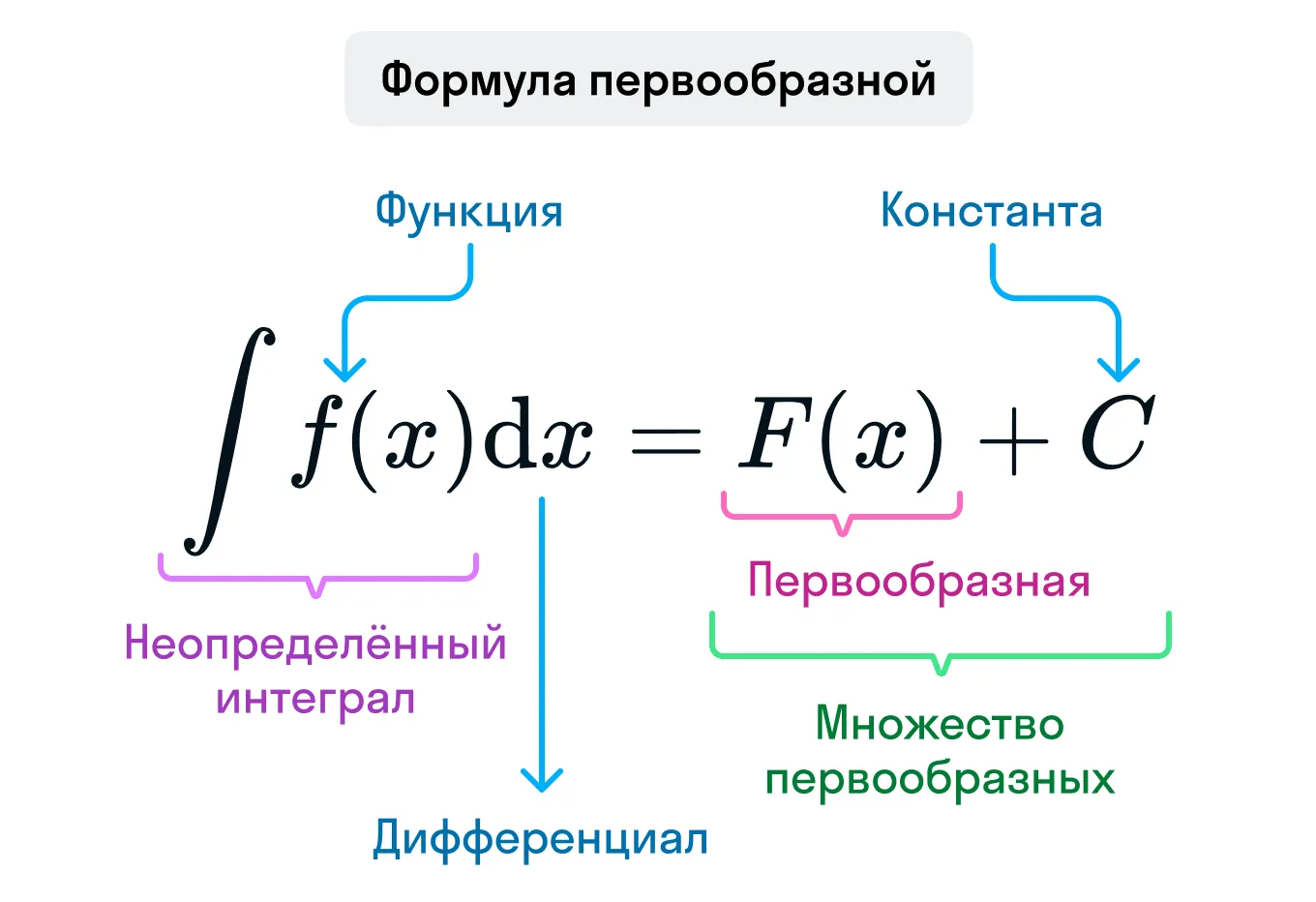
Первообразная для функции f(x) — это такая функция F(x), производная которой равна f(x). То есть выполняется равенство F'(x) = f(x).

Пример 1: мы знаем, что ускорение является производной от скорости. Тогда по нему можно найти скорость, восстановив функцию и найдя его первообразную.

Пример 2: производная функции –sin(x). Посмотрим внимательно в таблицу производных: cos'(x) = –sin(x). Тогда первообразная функции sin(x) будет равна –cos(x) + С с учётом постоянной величины.

Константа

Зачем добавлять константу к первообразной?

Представьте, что нам необходимо найти производную функций:

−cos(x) + 3,
−cos(x) + 5,
−cos(x) − 6.

Тогда производная будет равна sin(x) для всех трёх вариантов, так как производная любого числа равна нулю:

(−cos(x) + 3)' = sin (x),
(−cos(x) + 5)' = sin (x),
(−cos(x) − 6)' = sin (x).

Выходит, что получить исходную функцию в первозданном виде невозможно, но учесть дополнительное слагаемое в виде числа нам нужно. Именно поэтому в первообразной добавляют константу «+ С». Выражение, которое имеет общий вид F(x) + С, называется множеством первообразных функции.

Отсюда вытекает свойство первообразной: любые две первообразные одной и той же функции отличаются друг от друга не более чем на постоянную величину C.

Правила нахождения первообразной

Нахождение первообразной функции технически связано с поиском неопределённого интеграла функции.

Неопределённый интеграл — это интеграл, для которого не задан промежуток интегрирования.

Важный момент: если продифференцировать можно любую функцию, то найти первообразную функции можно не всегда.

Об этом говорит достаточное условие интегрируемости: если на некотором промежутке функция непрерывна, то она интегрируема на нём.

Каким образом можно найти первообразную функцию? Всё просто! Как и в случае с производной, мы можем воспользоваться готовой таблицей первообразных и свойствами неопределённого интеграла!

13. «Высокий» логарифм:

14. «Длинный» логарифм:

Свойства неопределённого интеграла

Свойства неопределённого интеграла можно назвать правилами интегрирования — основываясь на них, мы сможем находить первообразную сложных функций, сводя их к лёгким.

1. Производная от неопределённого интеграла равна подынтегральной функции; дифференциал от неопределённого интеграла равен подынтегральному выражению:

2. Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:

3. Константу можно вынести из-под знака интеграла: то есть, если , то .

4. Неопределённый интеграл от алгебраической суммы функций равен алгебраической сумме интегралов:

Примеры решения заданий

Задание 1

Найди первообразную функции

1. Записываем неопределённый интеграл:

2. Применяем свойство неопределённого интеграла об алгебраической сумме функций:

3. Выносим константы за знак интеграла:

4. Проводим интегрирование согласно таблице первообразных:

Задание 2

Вычисли неопределенный интеграл

1. Раскрываем скобку по формуле квадрата суммы и вносим х в скобку:

2. Воспользуемся свойством неопределенного интеграла об алгебраической сумме функций, выносим константы за знак интеграла и находим первообразную:

Интегрирование и нахождение первообразной — одна из самых сложных, но одновременно интересных тем алгебры. Иногда задания похожи на головоломку: необходимо выбрать верный способ решения, учесть все нюансы, выполнить верные вычисления. Научиться выполнять такие задания можно на уроках онлайн-курса математики в школе Skysmart: там вы не только подготовитесь к экзаменам, но и научитесь находить нестандартные решения, мыслить логически и строить самые неопровержимые доказательства.