Практикуйся по этой теме! Пройди задание №19 ЕГЭ по профильной математике |
Ноль - это целое число, которое на числовой прямой разделяет положительные и отрицательные числа.
Пример: 0 находится между -1 и 1.
Определение целых чисел
Что такое целое число — это натуральное число, а также противоположное ему число и нуль. Примеры целых чисел: -7, 222, 0, 569321, -12345 и др.
Что важно знать о целых числах:
- Сумма, разность и произведение целых чисел в результате дают целые числа.
- Не существует самого большого и самого маленького целого числа. Этот ряд бесконечен. Наибольшего и наименьшего целых чисел — не бывает.
- Обыкновенные и десятичные дроби нельзя назвать целыми числами. Но иногда в задачах можно встретить целые числа, у которых дробная часть равна нулю и при этом нет долей.
Целые числа на числовой оси выглядят так:
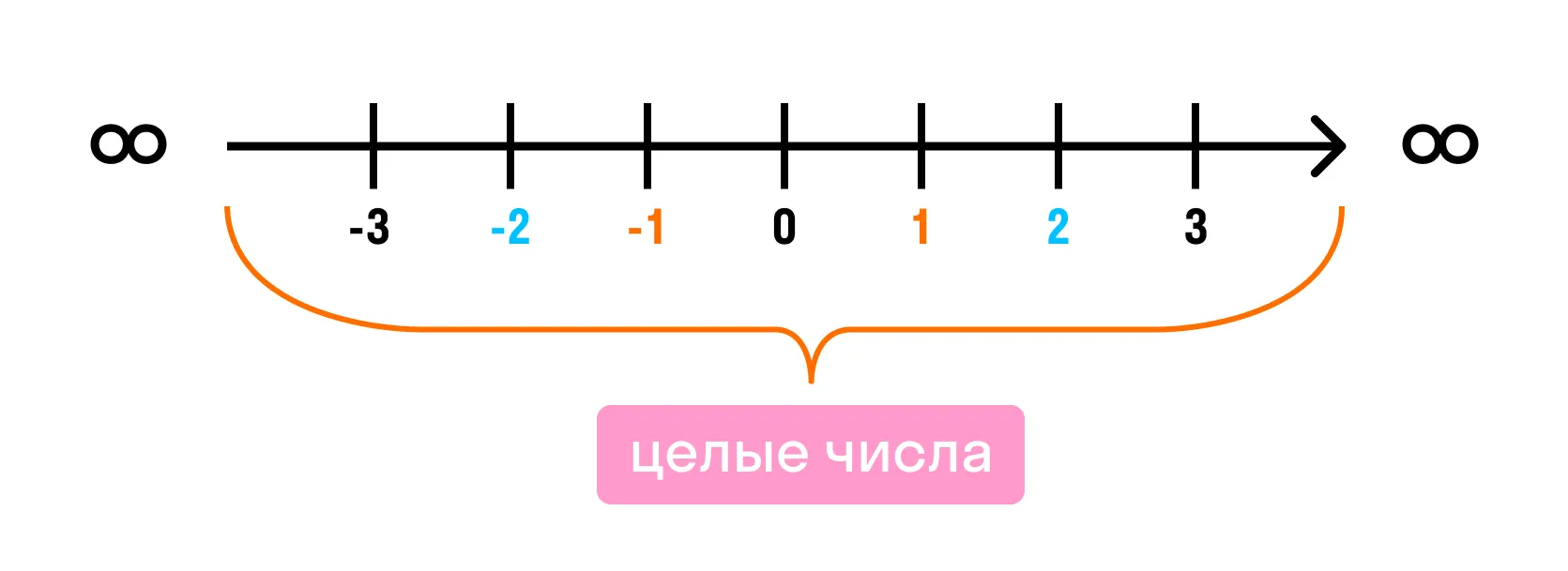
На координатной прямой начало отсчета всегда начинается с точки 0. Слева находятся все отрицательные целые числа, справа — положительные. Каждой точке соответствует единственное целое число.
В любую точку прямой, координатой которой является целое число, можно попасть, если отложить от начала координат данное количество единичных отрезков.
Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.
Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и противоположные натуральным отрицательные числа. Множество целых чисел обозначают Z.
Выглядит эти ребята вот так:
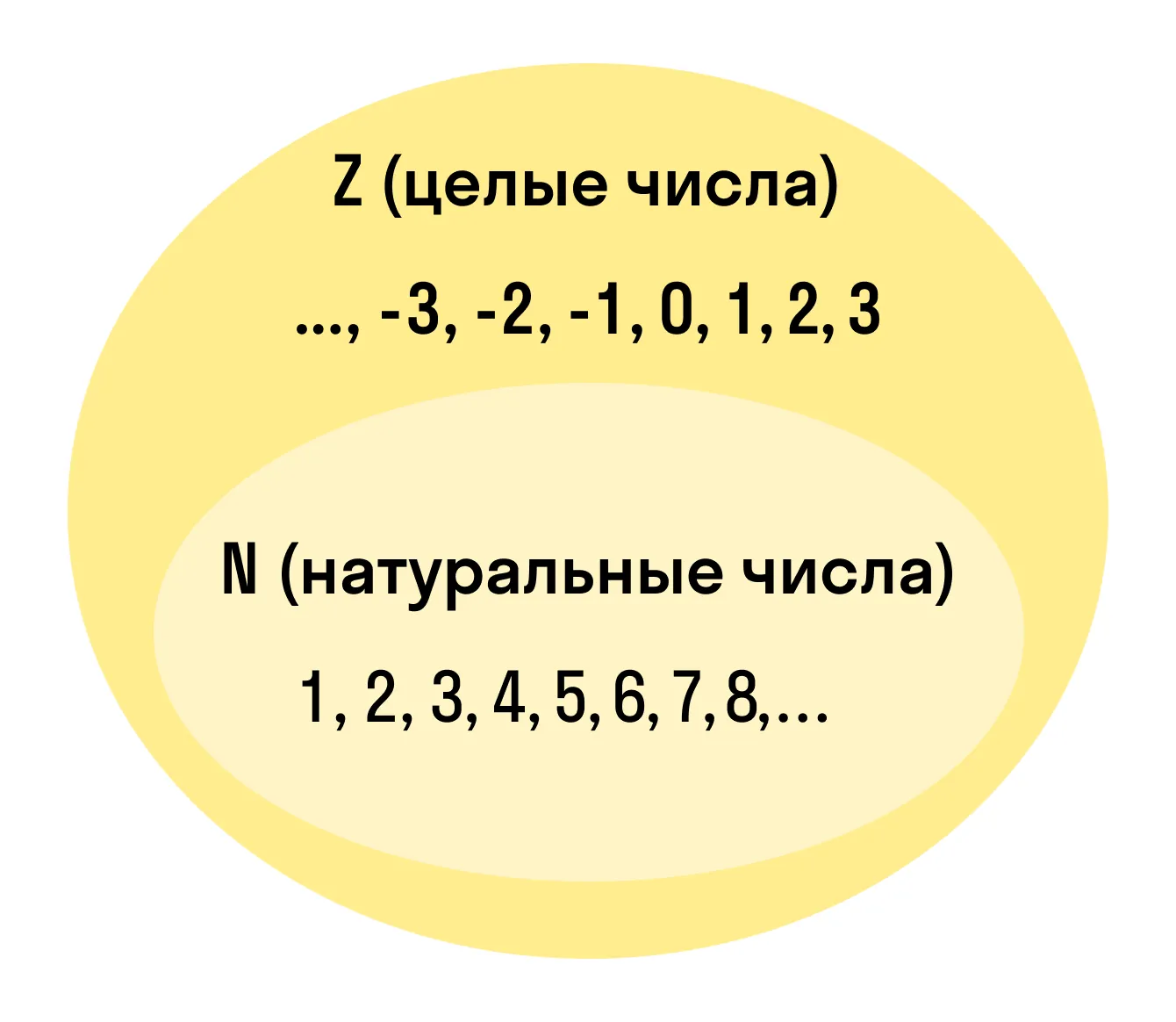
Последовательность целых чисел можно записать так:
∞ + ... -4, -3, -2, -1, 0, 1, 2, 3, 4 … + ∞
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Свойства целых чисел
Таблица содержит основные свойства сложения и умножения для любых целых a, b и c:
|
Свойство |
Сложение |
Умножение |
|
Замкнутость |
a + b — целое |
a × b — целое |
|
Ассоциативность |
a + (b + c) = (a + b) + c |
a * (b * c) = (a * b) * c |
|
Коммутативность |
a + b = b + a |
a * b = b * a |
|
Существование нейтрального элемента |
a + 0 = a |
a * 1 = a |
|
Существование противоположного элемента |
a + (−a) = 0 |
a ≠ ±1 ⇒ 1/a не является целым |
|
Дистрибутивность умножения относительно сложения |
a * (b + c) = (a * b) + (a * c) |
|
Пару слов о делении. В стандартном виде невозможно разделить число на множестве целых чисел, но можно делить с остатком. Это правило можно сформулировать так:
- Для всяких целых a и b (b ≠ 0), есть один набор целых чисел q и r. При этом:
a = bq + r, где a — делимое, b — делитель, q — частное, r — остаток,
0 ≤ r < |b|, где |b| — абсолютная величина (модуль) числа b.
Получи больше пользы от Skysmart:
-
Прокачивай знания на курсах математики.
-
Выбирай из 1200+ репетиторов по математике.
Записывайся на бесплатные курсы для детей.
Положительные и отрицательные целые числа
Ряд целых чисел состоит из положительных и отрицательных чисел. Справа от нуля живут натуральные числа — их еще называют целыми положительными числами. А слева от нуля — целые отрицательные числа.
Отрицательные целые числа — это целые числа со знаком «минус». Они всегда меньше нуля. Примеры целых отрицательных чисел: -944, -1287, -1, -19.
Положительные целые числа — это целые числа со знаком «плюс». Они всегда больше нуля. Примеры положительных целых чисел: 13, 401, 55, 29, 12345.
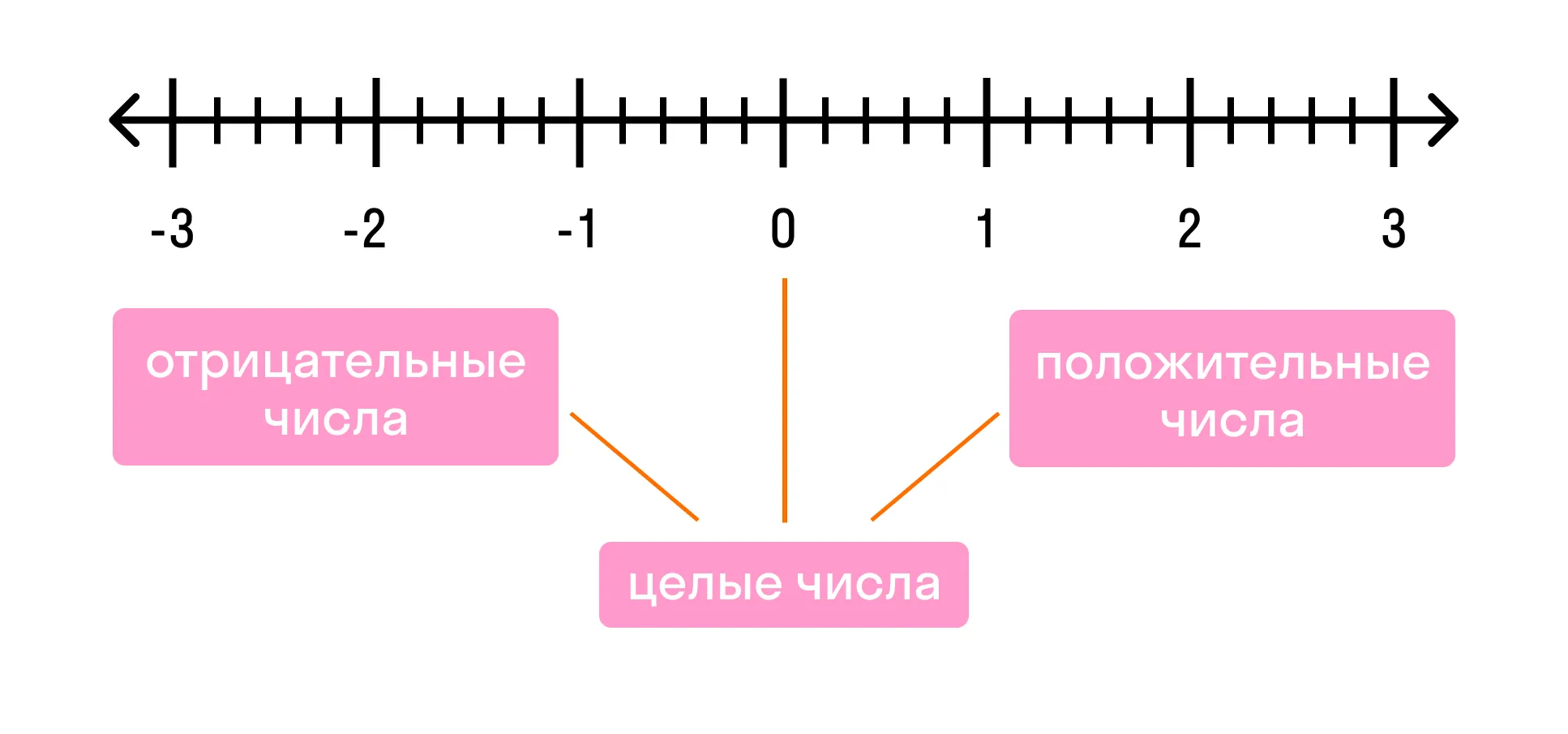
Бесконечное множество — это ряд целых чисел в положительную и в отрицательную сторону.
Если выбрать два любых целых числа, то те числа, которые находятся между заданными, можно называть конечным множеством.
Например, напишем целые числа от -4 до 3. Все числа, стоящие между этими числами, входят в конечное множество. Данное конечное множество чисел выглядит так:
- -3, -2, -1, 0, 1, 2
Пример 1. Сколько целых чисел расположено между числами -30 и 100?
Как рассуждаем:
- Можно построить прямую и посчитать сколько отрезков находится между заданными числам.
- Или можно посчитать в уме: у нас есть 29 отрицательных числа, нуль и 99 положительных чисел.
29 + 1 + 99 = 129
Ответ: 129.
Пример 2. Сколько нечетных целых чисел расположено между числами -4 и 5?
Как рассуждаем:
- Выпишем все целые числа, которые находятся между -4 и 5:
-3, -2, -1, 0, 1, 2, 3, 4 - Подчеркнем нечетные числа в данному ряду.
Ответ: -3, -1, 1, 3.
Неположительные и неотрицательные целые числа
Неотрицательные целые числа — это положительные целые числа и число нуль. Примеры неотрицательных целых чисел: 43, 878, 0.
Неположительные целые числа — это отрицательные целые числа и число нуль. Примеры неположительных целых чисел: -43, -878, 0.
Нуль — это граница между положительными и отрицательными числами. То есть нуль это ни положительное и ни отрицательное число.
Эти два термина помогают формулировать мысли кратко. Например, вместо того, чтобы говорить, что число a — целое число, которое меньше или равно нулю, можно сказать: a — целое неположительное число.
Целые числа в описании изменения величины
Какие числа называют целыми мы уже знаем. Их удобно использовать, чтобы считать предметы или чтобы сказать, что чего-то стало больше или меньше. А теперь примерчик!
Вы участвуете в конкурсе в инстаграм: нужно написать 5 постов про свои самые заветные мечты. А пока вы это не сделали, можно сказать, что сейчас у вас -5 постов. То есть число 5 описывает сколько вы должны сделать постов, а знак «минус» говорит о том, что вы все еще не выполнили условия конкурса. Постов то нет🙄
А если помимо 5 постов, нужно опубликовать еще 5 сторис — общий долг можно вычислить по правилу сложения отрицательных чисел:
- -5 (постов, которых еще нет) + (-5 сториз, которых тоже еще нет) = -10 публикаций
Итого: чтобы участвовать в конкурсе, нужно сделать 10 публикаций в инстаграм.
