Длина окружности - это расстояние вокруг неё. Вычисляется по формуле:
Альтернативно, с использованием радиуса:
Например, для окружности с диаметром 10 см, длина окружности будет
Для кого эта статья:
- Студенты и школьники, изучающие геометрию
- Педагоги и преподаватели, ищущие ресурсы для объяснения материала
- Специалисты и инженеры, занимающиеся расчетами в строительстве и дизайне
Онлайн-калькулятор длины окружности
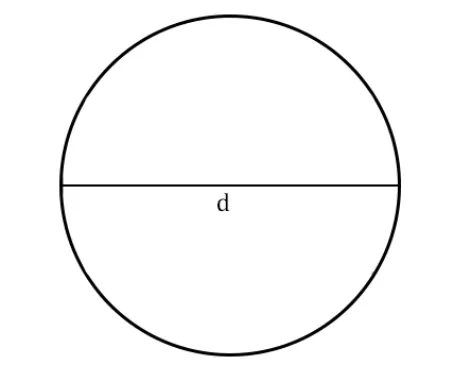
Формула длины окружности через диаметр: l=πd, где π — число пи, математическая константа, примерно равная 3,14, d — диаметр окружности.

Как найти длину окружности через диаметр
Чтобы найти длину окружности, зная диаметр, умножьте диаметр на число пи (π).
Формула:
Пример: если диаметр (d = 10) см, тогда длина окружности
Хорда — это отрезок, который соединяет две точки окружности.
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
l=πd, где
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Получи больше пользы от Skysmart:
-
Подготовься к ОГЭ на пятёрку
-
Подготовься к ЕГЭ на высокие баллы
Записывайся на бесплатные курсы для детей
Решай задания в бесплатном тренажёре ЕГЭ
Как найти длину окружности через радиус
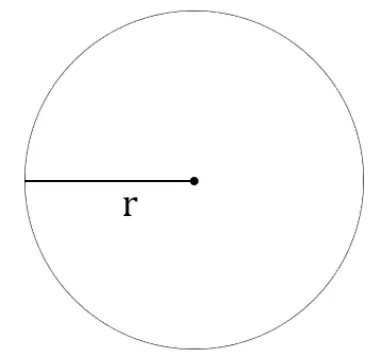
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
l=2πr , где
π — число пи, примерно равное 3,14
r - радиус окружности
Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, примерно равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
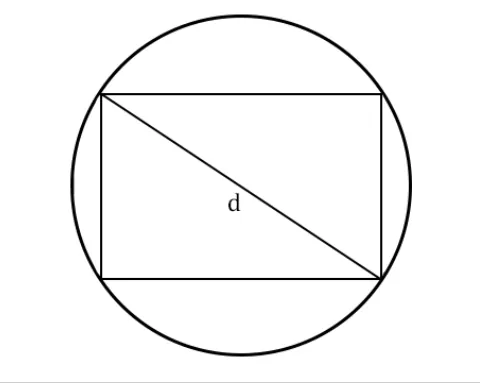
l=πd, где
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
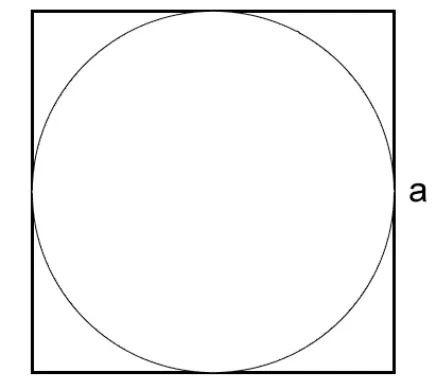
l=πa, где
π - математическая константа, примерно равная 3,14
a - сторона квадрата
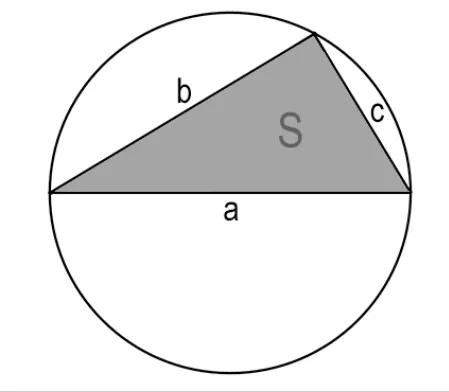
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника

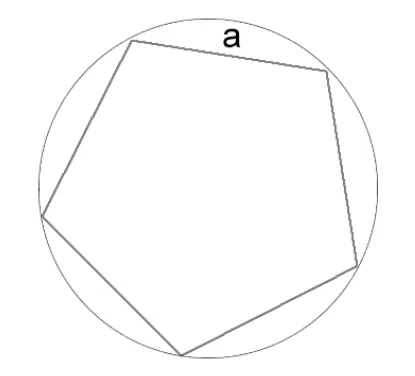
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Ответ: 15,7 (см)
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною
Решение. Радиус окружности равен
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус
Так и сделаем:
Ответ:
Обучение на курсах по математике поможет закрепить полученные знания на практике.



















