Рациональные уравнения

Что такое рациональные уравнения

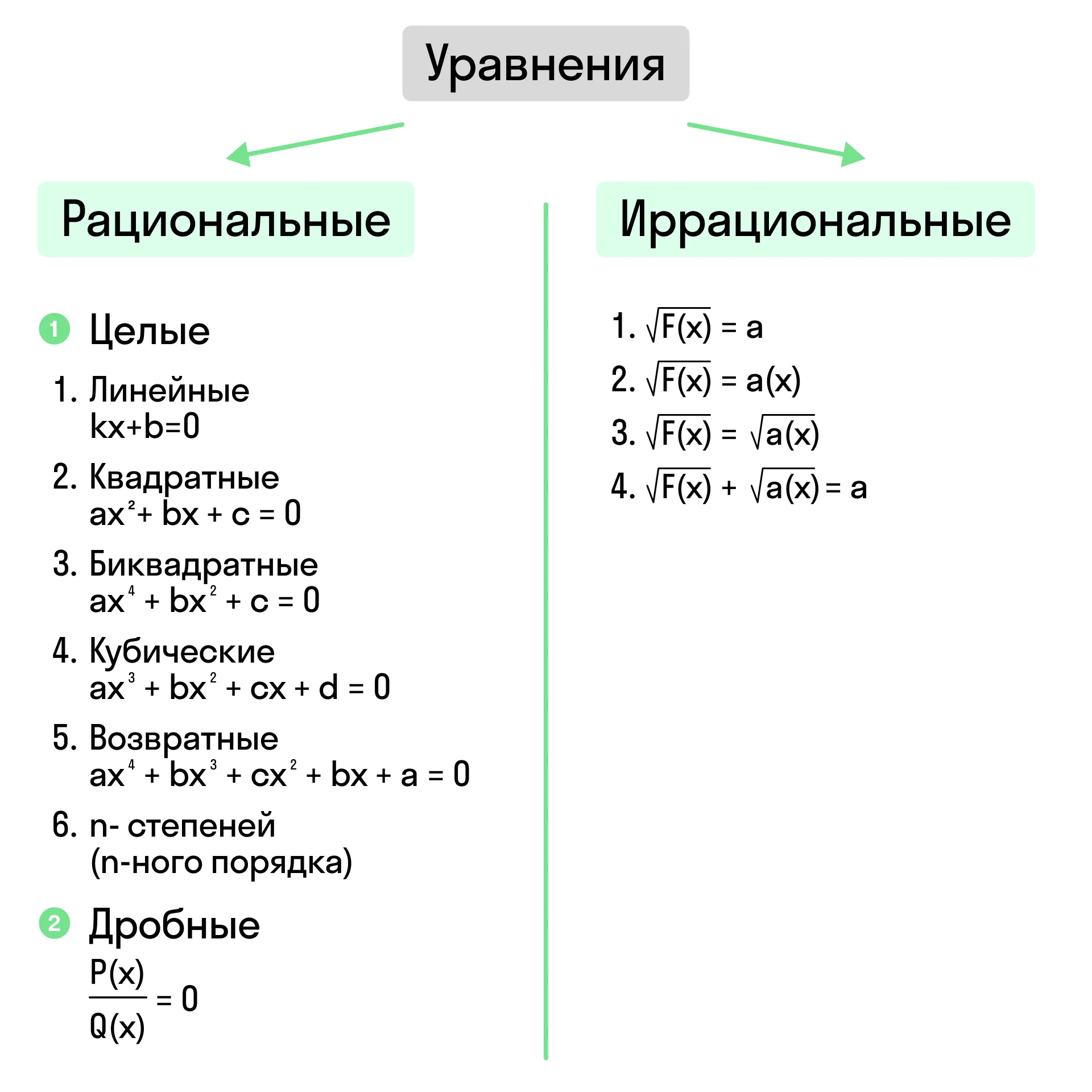
Давайте начнём с понятия рационального выражения.

Рациональное выражение — это математическое выражение, составленное из чисел, переменных (букв) и действий (сложение, вычитание, умножение, деление, возведение в целую степень).

В рациональных выражениях не встречаются корни и дробные степени — это самое важное!

Рациональные выражения	Иррациональные выражения

Рациональные уравнения — это уравнения, в состав которых входят только рациональные выражения.

Целые рациональные уравнения

Целые рациональные уравнения делятся на 6 видов, только 5 из которых подробно изучаются в школьной программе.

Линейные уравнения

Общий вид линейных уравнений: kx + b = 0, где k, b — числа.

Главные признаки линейного уравнения:

1. Неизвестная находится в первой степени.

2. Неизвестная находится строго в числителе дроби, если в уравнении представлены дроби. Если неизвестная находится в знаменателе, то такое уравнение — дробно-рациональное.

Для решения такого уравнения необходимо:

• привести его к стандартному виду kx + b = 0;

• перенести свободный член b в правую сторону со сменой знака;

• выразить неизвестную x: .

Например:

2(x − 4) + 3(x + 6) = 0

2x − 8 + 3x + 18 = 0

5x + 10 = 0

5x = −10

x = −10/5 = −2

Квадратные уравнения

Общий вид квадратных уравнений: ax² + bx + c = 0, где a, b, c — числа и a ≠ 0.

Квадратные уравнения бывают:

1. Неполными (когда b = 0 или с = 0).

2. Полными (когда a, b, c ≠ 0).

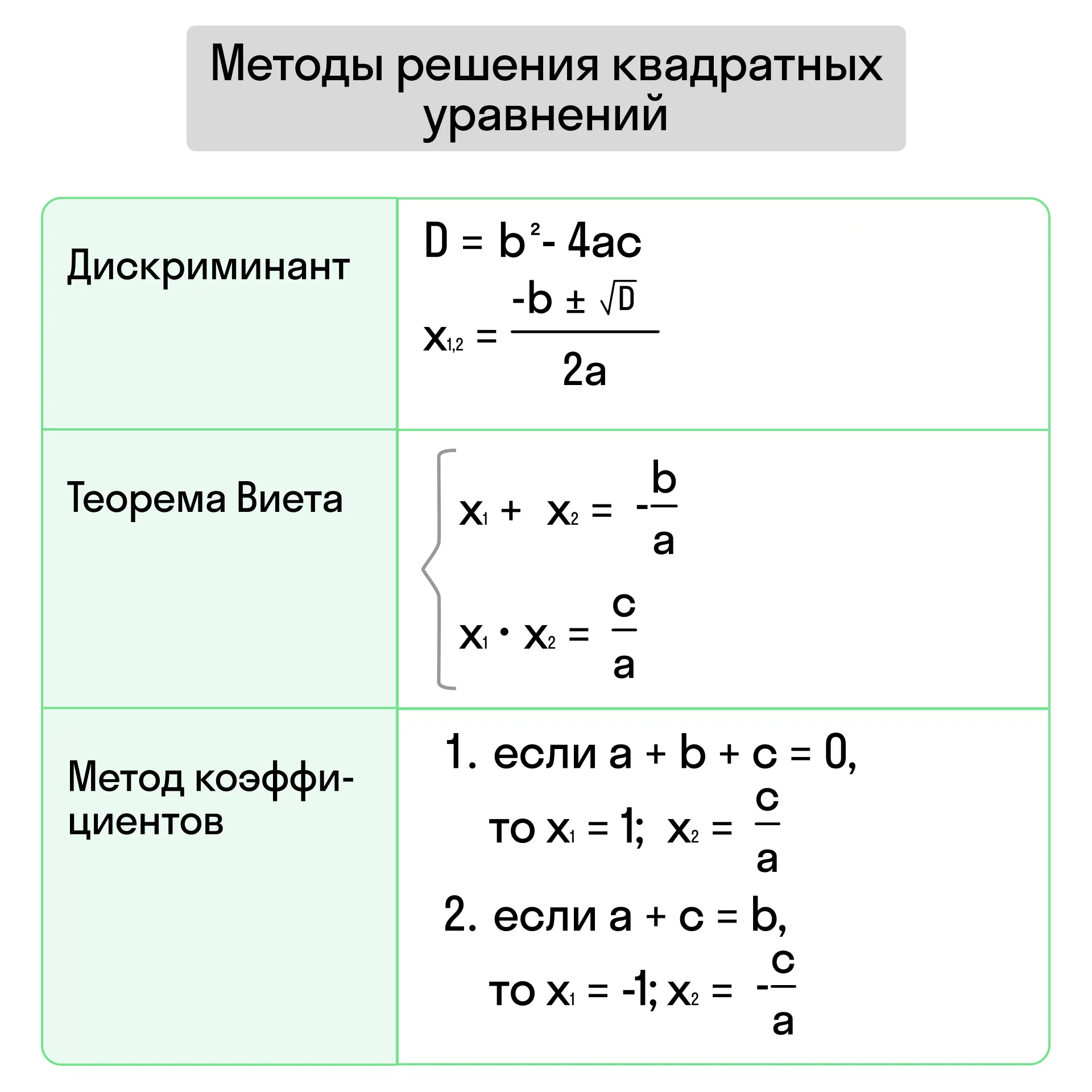
Для решения квадратных уравнений применяют различные методы: через дискриминант, через теорему Виета, с помощью свойств коэффициентов, графически и даже геометрически! Но конечно, самые популярные способы — это дискриминант, теорема Виета и свойства коэффициентов квадратного уравнения.

Дискриминант	Теорема Виета	Метод коэффициентов
	тогда

Биквадратные уравнения

Общий вид биквадратных уравнений: ax⁴ + bx² + c = 0, где a, b, c — числа и a ≠ 0.

Такие уравнения сводятся к квадратным с помощью замены переменной.

Пусть , тогда

Тогда:

Кубические уравнения

Общий вид кубических уравнений: ax³ + bx² + cx + d = 0, где a, b, c, d — числа и a ≠ 0.

Кубические уравнения, также как и квадратные, бывают полными и неполными (когда один из коэффициентов b, c, d равен нулю или все они равны нулю). Методов решения кубических уравнений достаточно много, но самое простое развитие событий — когда уравнение можно разложить на множители.

5x³ − x² − 20x + 4 = 0

(5x³ − x²) − (20x − 4) = 0

x²(5x − 1) − 4(5x − 1) = 0

(5x − 1)(x² − 4) = 0

Так как произведение равно нулю, мы можем разбить это уравнение на два маленьких, приравняв к нулю каждую из скобок.

5x − 1 = 0 x = 0,2

x2 − 4 = 0 (x + 2)(x − 2) = 0 x = 2 или х = −2

Возвратные уравнения

Общий вид возвратных уравнений: ax⁴ + bx³ + cx² + bx + a = 0, где a, b, c, d — числа и a ≠ 0.

Уравнения такого типа решаются следующим образом:

1. Обе части уравнения делим на x²:

1. Группируем слагаемые с равными коэффициентами и выносим их как общий множитель:

2. Производим замену переменной:

   Пусть , тогда

3. Уравнение с учётом замены переменной выглядит так:

   Решаем уравнение относительно переменной y и по её значением находим x:

   Замена:

   Тогда

   /p>

ОДЗ: x ≠ 0

160.3K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Дробно-рациональные уравнения

Общий вид дробно-рациональных уравнений: , где P(x), Q(x) — рациональные выражения. То есть в дробно-рациональных уравнениях выражение представлено в виде дроби, где в знаменателе (а порой и в числителе тоже) есть неизвестная.

Главная отличительная особенность решения таких уравнений — поиск ОДЗ (область допустимых значений).

Так как на ноль делить нельзя, а дробная черта представляет собой действие деления, знаменатель не может превращаться в ноль. Мы должны оценить, какие значения можно подставить вместо x, а какие нам нужно исключить.

Например:

В выражении ОДЗ: x ≠ 2, так как при x = 2 выражение принимает вид , что является ошибкой.

Важно

При решении подобных уравнений во второй части ОГЭ и профильного ЕГЭ по математике указывать ОДЗ обязательно! Если этот пункт пропустить, решение не засчитают, даже если вы получили верные корни уравнения.

Давайте рассмотрим некоторые виды дробно-рациональных уравнений и методы их решения.

Первый вид дробно-рациональных уравнений

Самый стандартный вид, где дробь равна нулю: .

Алгоритм решения:

1. Исследуем ОДЗ.

2. Приравниваем числитель к нулю и находим значение переменной (знаменатель откидываем).

3. Анализируем полученные корни, сравниваем с ОДЗ.

ОДЗ: x ≠ −2

x² + 5x + 6 = 0

x₁ = −3; x₂ = −2 — не соответствует ОДЗ

Ответ: x = −3

Второй вид дробно-рациональных уравнений

В этом случае в уравнении приравнены друг к другу дроби с одинаковыми знаменателями: .

Алгоритм решения:

1. Исследуем ОДЗ.

2. Приравниваем числители дробей друг к другу и находим значение переменной (знаменатели откидываем).

3. Анализируем полученные корни, сравниваем с ОДЗ.

ОДЗ: x ≠ 3

x² − 6 = x

x² − x − 6 = 0

D = 1 + 6 ⋅ 4 = 25

x₁ = 3 — не соответствует ОДЗ

x₂ = −2

Ответ: x = −2

Третий вид дробно-рациональных уравнений

В этом случае в уравнении приравнены друг к другу дроби с разными знаменателями, причём дробей может быть больше двух: .

Если дробей две, мы можем пойти по следующему алгоритму:

1. Исследуем ОДЗ.

2. Пользуемся основным свойством пропорции: перемножаем средние и крайние члены пропорции накрест. Решаем полученное уравнение и находим значения неизвестной.

3. Анализируем полученные корни, сравниваем с ОДЗ.

   ОДЗ:

Ответ: x₁ = 4; x₂ = 3

Если в уравнении представлена сумма дробно-рациональных выражений, где слагаемых три и более, а знаменатели разные, мы делаем так:

1. Исследуем ОДЗ.

2. Приводим все дроби к одинаковому знаменателю.

3. Откидываем знаменатели и решаем полученное уравнение без них.

4. Анализируем полученные корни, сравниваем с ОДЗ.

ОДЗ:

— оба корня не соответствуют ОДЗ

Ответ:

Разобраться в решении рациональных уравнений бывает непросто, поэтому так важна постоянная практика! Отличным помощником в этом деле сможет стать бесплатный тренажёр ЕГЭ от Skysmart. С ним вы легко и быстро сможете отработать любую тему, проверить свои знания и подготовиться к контрольной работе и экзаменам.