Логарифмы и онлайн-калькулятор логарифмов

Что такое логарифм?

Нагляднее всего понять это с помощью графического решения уравнений. Начертим график и с его помощью решим уравнения:

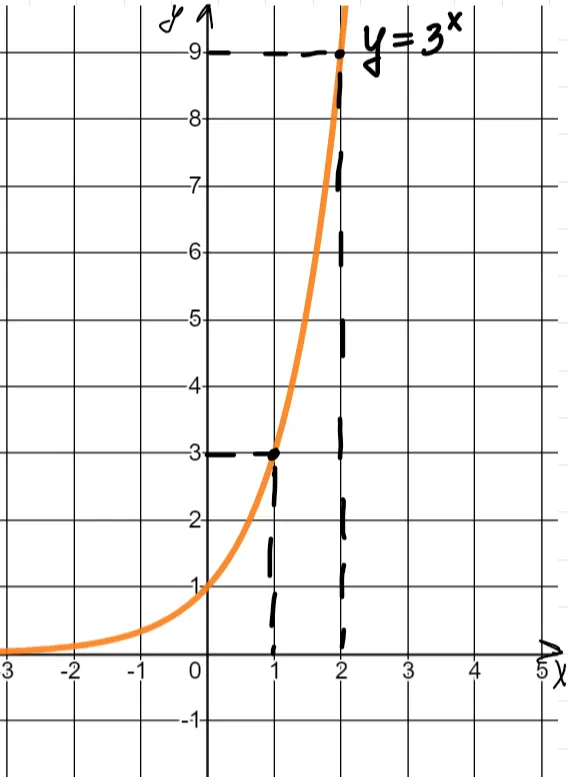
x = 1

x = 2

Отлично! А теперь решим уравнение .

И в этом случае невозможно назвать точное значение, то есть мы понимаем, что корень больше одного и меньше двух, но более точных данных нет.

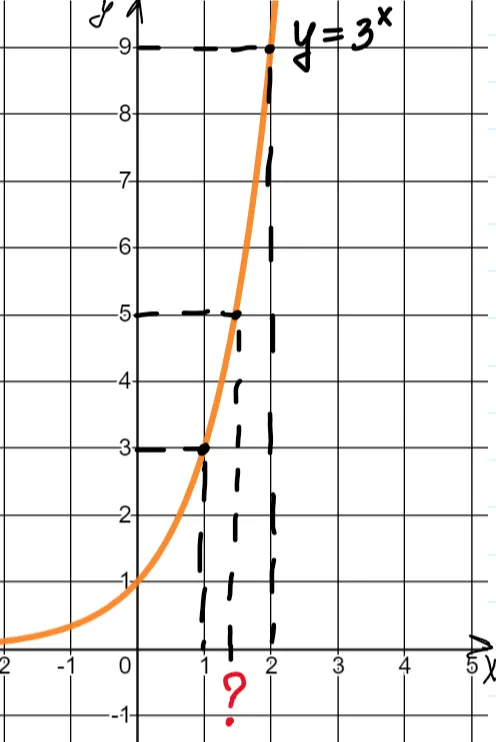
Вот такой корень и задается с помощью логарифма, а именно (читается как «логарифм пяти по основанию три» или «логарифм по основанию три от пяти»).

Мы определили смысл — теперь перейдем к общему определению логарифма.

Логарифмом числа b по основанию a называют показатель степени с основанием a, равной b. То есть, попросту говоря, логарифм — это степень, в которую нужно возвести a для получения b. Однако у логарифма есть условия или ограничения, что основание а больше нуля и не равно единице, а также показатель b больше нуля.

178.1K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Как решать примеры с логарифмами?

Рассмотрим пример, как решить логарифм:

Задаем вопрос: в какую степень нужно возвести 7, чтобы получить 49?

Ответ: во вторую степень. Значит, .

Какие бывают виды логарифмов?

Логарифм по основанию 10 называется десятичным логарифмом и обозначается как . Пример десятичного логарифма: .

Логарифм по основанию e называется натуральным логарифмом и обозначается как . Пример натурального логарифма: .

Свойства и формулы логарифмов

1. Эта формула называется основным логарифмическим тождеством.

   Пример: .

2. Пример: .

3. Пример: .

4. Логарифм степени находится по формуле: .

   Видно, что показатель степени выносим перед логарифмом.

   Пример: .

5. Показатель степени основания также выносим перед логарифмом, но в виде обратного числа, то есть, например, вместо 5 будет .

   Пример: .

6. Если нужно перейти к другому основанию, то можно сделать это по формуле: . Свойство называется формулой перехода к новому основанию.

7. А частным случаем предыдущей формулы является формула, которая позволяет менять местами основание и аргумент логарифма: .

Конечно, это не все свойства логарифмов, а только самые главные. Комбинируя свойства выше, можно получать все новые и новые формулы для логарифмов. Например, соединив 4-ю и 5-ю формулы, получим . Но запоминать ее нет смысла, важно знать лишь базовые свойства логарифмов.

Применение логарифмических свойств в примерах

Пример 1

Найдите значение выражения , если .

Если видите частное в показателе логарифма, то распишите по 3-й формуле: .

Решение

У каждого логарифма в показателе стоит степень, значит, поможет 4-я формула:

.

Первый логарифм можно вычислить по определению. И обратите внимание на второй логарифм: у него в основании стоит а, а в условии задачи дан логарифм с основанием b, значит, нужно а как-то заменить на b. Возможно ли это? Конечно, 7-я формула в помощь!

.

Подставьте числовое значение из условия, и все готово:

.

Отличный пример! Мы использовали практически все свойства логарифмов. А теперь попрактикуйтесь еще, но помните, что задача с подвохом!

Пример 2

Вычислите: .

Получился ответ 27? Если да, то поздравляю: вы попались на удочку самых популярных ошибок! Какое бы задание вам ни встретилось, действия с логарифмами нужно производить только по определениям и правилам. В примере вы видите деление двух логарифмов. А есть ли какая-то формула, в которой записано деление двух логарифмов?

Конечно, это формула перехода к новому основанию, которую мы привели в пункте 6 выше. Применим ее к этому случаю и вычислим логарифм по определению, задав вопрос: в какую степень нужно возвести основание, чтобы получился показатель?

.

И получается ответ 4, а не 27.

Практическое применение логарифмов

Помните, выше мы говорили, что логарифм объединяет задания на ЕГЭ, галактики и рога горных козлов? И если с баллами на ЕГЭ все понятно, то про галактики и рога — интереснее.

Все дело в том, что существует логарифмическая спираль, которая задается по формуле: . По этой логарифмической спирали растут рога горных козлов, закручены многие галактики (и даже та, в которой мы живем), а также раковины некоторых морских животных, усики растений, ураганы, смерчи и многое другое.

Как видите, логарифмы имеют большое значение для нашей жизни — не только баллы на ЕГЭ!

Тест по теме «Логарифмы»

Найдите \log_a\sqrt[3]{\dfrac ab}, если \log_ab=10.

Ответ: -3 .

Найдите \log_a(a^2\sqrt b) , если \log_ba=\dfrac{1}{10} .

Ответ: 7 .

\log_{5} 31,25 - \log_{0,2} 4.

Ответ: 3 .

7^{3+\log_{7}{5}}

Ответ: 1715 .

\log_5\dfrac12\cdot\log_2\dfrac17\cdot\log_7\dfrac15= -1

\log_{0,05} 5 + \log_{\frac{1}{20}} 4.

Ответ: -1 .

Найдите значение выражения \log_a(ab^3), если \log_ba=\dfrac17.

Ответ: 22 .

11\cdot6^{\small \log_6{2}}

Ответ: 22

Найди значение выражения, \log_{a}{(a^3b^3)} если \log_ab=-2.

Ответ: -3 .

\log_{\small\frac{1}{11}}{\sqrt{11}}

Ответ: -0,5 .

Вопросы для самопроверки

Чтобы информация точно усвоилась, вспомните:

1. Что такое логарифм?

2. Какие ограничения есть у логарифма?

3. Какие логарифмические свойства вы знаете?

4. Какие бывают способы преобразования выражений с логарифмом?

5. В чем практическое применение логарифмов?

На курсах по математике в онлайн-школе Skysmart мы всегда показываем, зачем нужны математические правила и формулы в реальной жизни — ведь так учиться гораздо интереснее! И подтянуть знания перед ЕГЭ тоже поможем: приходите на бесплатный вводный урок и все увидите сами.