Прямоугольный треугольник

23.8K

«Гипотенуза, катет, пифагоровы тройки»… Может показаться, что эти слова скорее относятся к географии и обозначают названия горных вершин или величественных водопадов. Но на деле куда интереснее! Из этой статьи вы узнаете, что такое прямоугольный треугольник, как с ним связаны понятия гипотенузы и катета, и какие есть лайфхаки для решения геометрических задач. Начнём?

Определение прямоугольного треугольника

Прямоугольный треугольник — это геометрическая фигура, многоугольник, у которого три стороны и три угла, причём один из углов прямой, т. е. равен 90°.

В прямоугольном треугольнике стороны имеют свои названия. Так, сторона, лежащая напротив прямого угла, называется гипотенузой, две остальные — катеты.

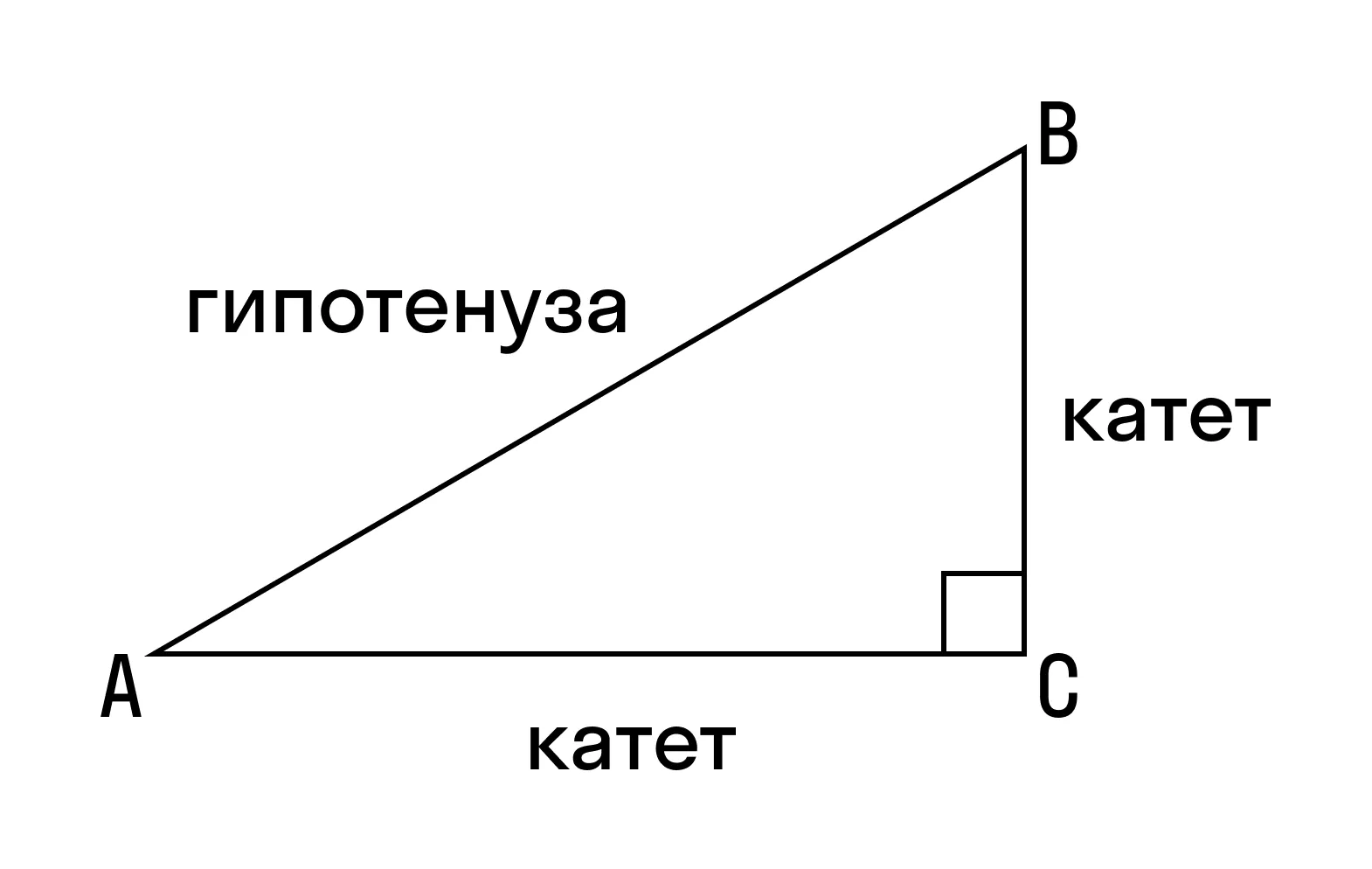
Гипотенуза — самая длинная сторона прямоугольного треугольника, т. к. лежит напротив бо́льшего угла.

Как вы думаете, может ли в прямоугольном треугольнике быть два прямых угла? А прямой и тупой угол? 🤔

Конечно же нет! Согласно свойствам, сумма углов в любом треугольнике равна 180°. На прямой угол приходится 90°, значит, на другие два — тоже 90°. Это полностью исключает возможность существования другого прямого или тупого угла в треугольнике такого типа.

Свойства прямоугольного треугольника

Сумма углов прямоугольного треугольника равна 180°.
Сумма острых углов прямоугольного треугольника равна 90°.
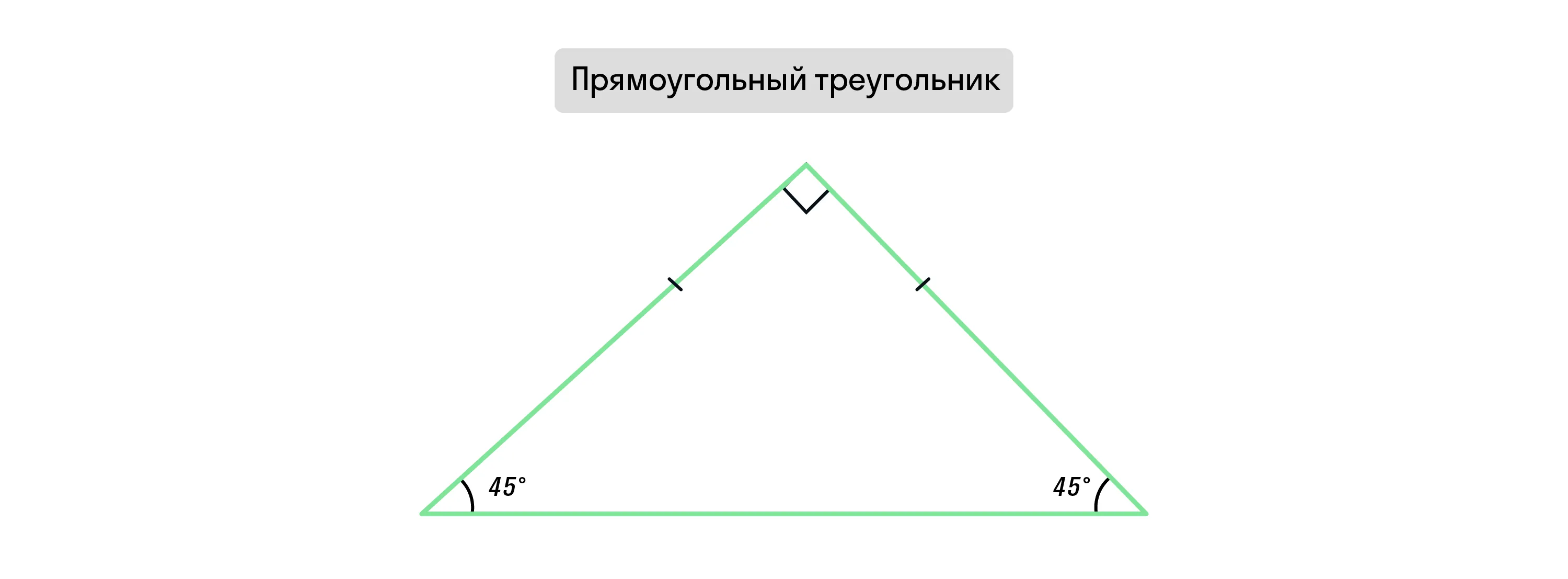
Если в прямоугольном треугольнике один из углов равен 45°, то такой треугольник равнобедренный.
Катет прямоугольного треугольника, лежащий против угла 30°, равен половине гипотенузы.

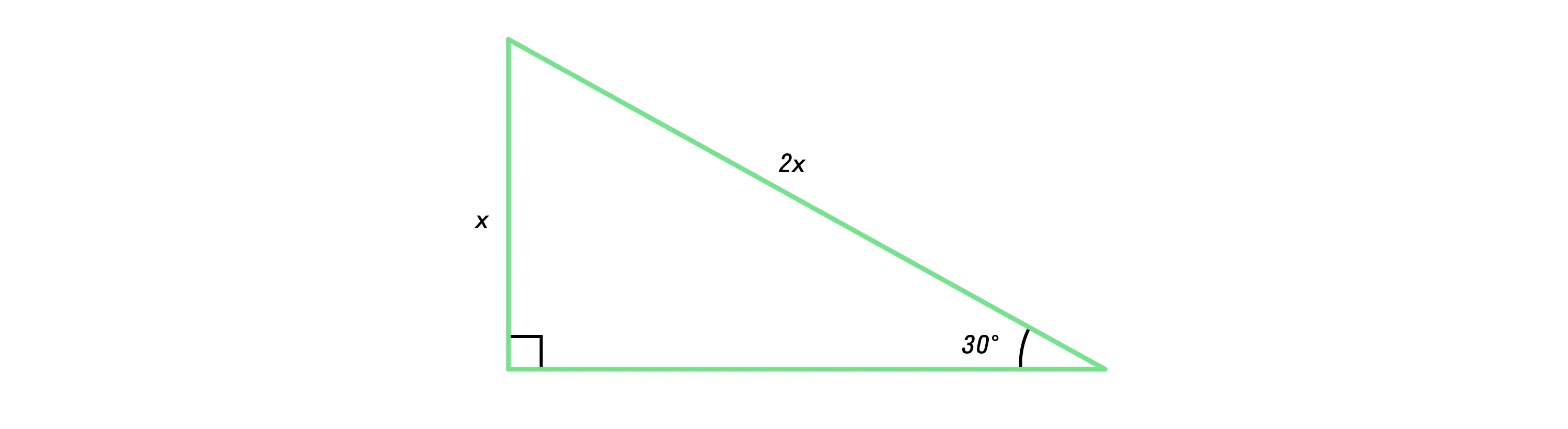
И наоборот, если катет прямоугольного треугольника равен половине гипотенузы, то противолежащий угол равен 30°.
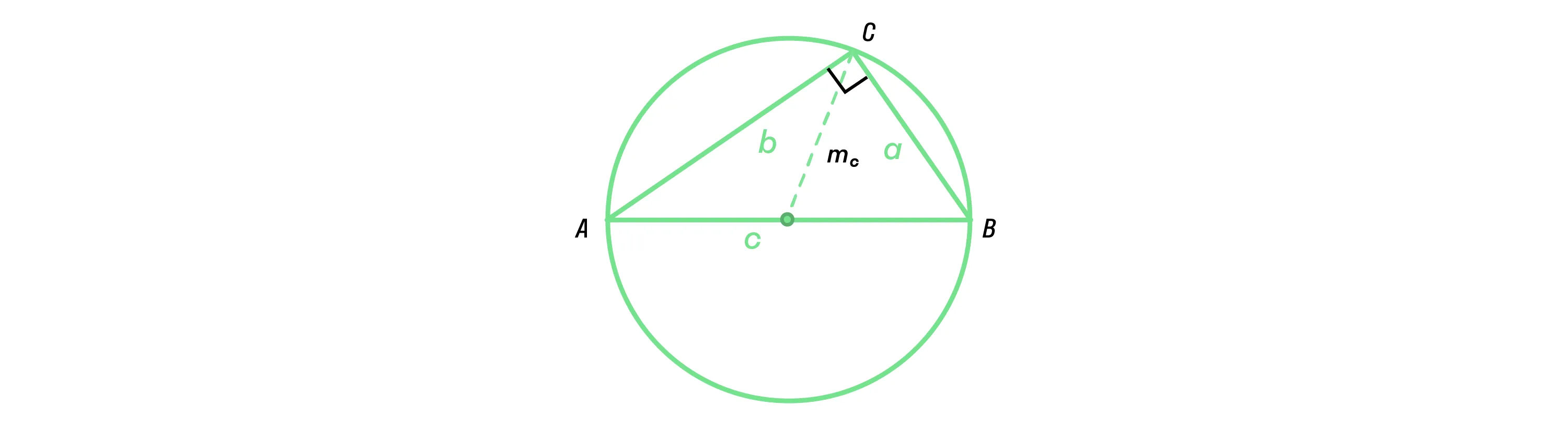
В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна её половине (и радиусу окружности, описанной около прямоугольного треугольника).
Центр окружности, описанной около прямоугольного треугольника, лежит на середине его гипотенузы.
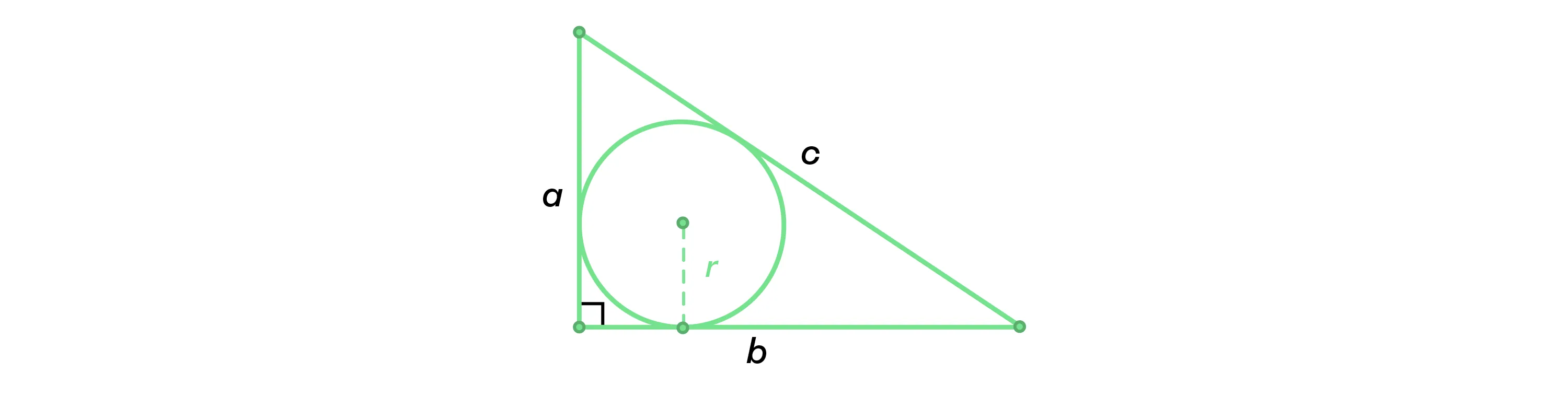
Радиус окружности, вписанной в прямоугольный треугольник, можно рассчитать по формуле: .

178.1K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

Подготовься к ОГЭ на пятёрку.
Подготовься к ЕГЭ на высокие баллы.
Записывайся на бесплатные курсы для детей.
Решай задания в бесплатном тренажёре ЕГЭ.

Основные формулы

Теорема Пифагора

Теорема Пифагора позволяет рассчитать длину одной из сторон прямоугольного треугольника по двум другим.

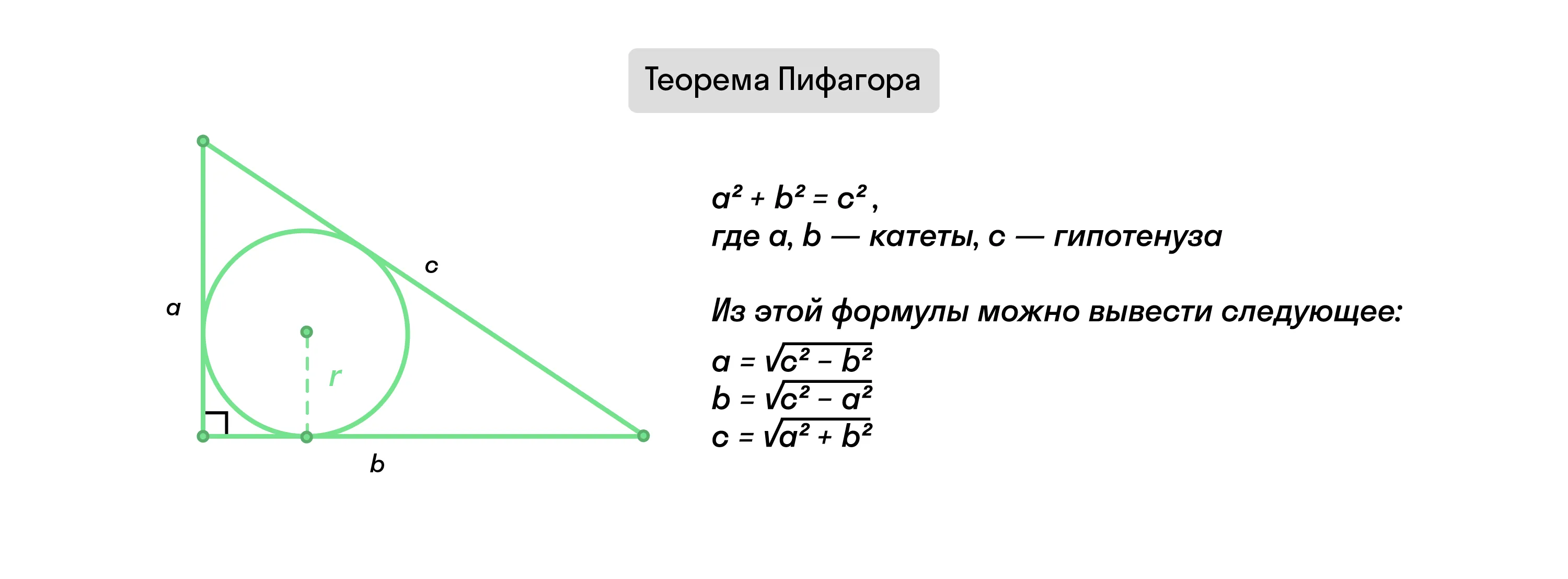
Сформулировать это правило можно так: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: .

Из этой формулы можно выразить катеты a и b и найти их длины, если это необходимо.

Так, если гипотенуза треугольника АВС равна 13, а один из катетов — 5, то другой катет равен .

Почему теорема так называется?

Общепринято, что доказательство этой теоремы вывел древнегреческий учёный и философ Пифагор. Его именем также названы и другие математические понятия, например, «Пифагоровы тройки». Это множества, состоящие из трёх натуральных чисел, которые удовлетворяют формуле , например или .

Таких множеств — бесконечное количество! Можно запомнить некоторые из них, чтобы быстро решать задачи на прямоугольные треугольники без применения теоремы Пифагора.

(3, 4, 5), (6, 8, 10),
(5, 12, 13), (9, 12, 15),
(8, 15, 17), (12, 16, 20),
(15, 20, 25), (7, 24, 25),
(10, 24, 26), (20, 21, 29),
(18, 24, 30), (16, 30, 34),
(21, 28, 35), (12, 35, 37),
(15, 36, 39), (24, 32, 40),
(9, 40, 41), (14, 48, 50), (30, 40, 50)...

Площадь и периметр прямоугольного треугольника

Периметр прямоугольного треугольника — сумма длин всех его сторон: P = a + b + c.

Площадь прямоугольного треугольника можно вычислить с помощью нескольких формул. Приведём самые базовые:

, где a и b — катеты прямоугольного треугольника.
, где a — катет, с — гипотенуза, — угол между катетом и гипотенузой.

Сохраняйте себе памятку с другими полезными формулами для нахождения площади треугольника — для экзаменов точно пригодится!

Скачать шпаргалку

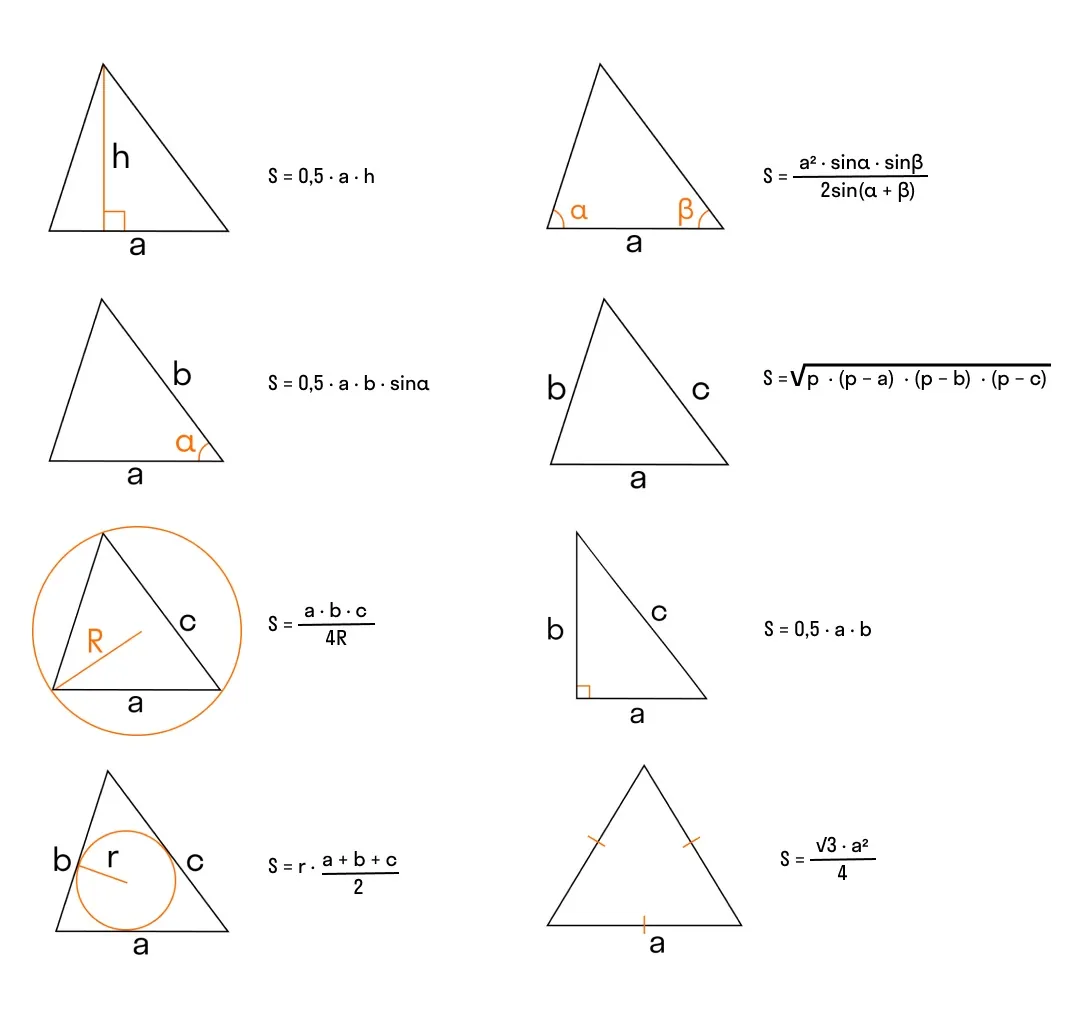
Если от объёма информации разбежались глаза — в этом нет ничего страшного. Чтобы запомнить все формулы и отработать навыки решения задач по теме «Прямоугольный треугольник», переходите по ссылке в наш бесплатный тренажёр ЕГЭ. Это удобный инструмент для подготовки к контрольным работам и экзаменам. Пользуйтесь с удовольствием!