Проверьте знания по математике бесплатно

Узнать бесплатно

Площадь круга: как найти, формулы и калькулятор

1.6K

Внимательное наблюдение за объектами округлых форм успокаивает нервную систему: рябь на воде, кольца дыма. Из этой статьи вы узнаете, как устроена эта идеальная фигура, чему равна ее площадь и как ее высчитывать.

Чтобы найти площадь круга, используют формулу , где ( S ) — площадь, ( r ) — радиус и . Через диаметр ( d ): . Через длину окружности ( L ): .

Примеры:

При радиусе 3 см: см²
При диаметре 10 см: см²

Для кого эта статья:

студенты и учащиеся, изучающие математику
люди, интересующиеся геометрией и её приложениями
пользователи, ищущие практические инструменты для расчетов (например, онлайн-калькуляторы)

Онлайн-калькулятор площади круга

Формула: S = π × r², где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.

Радиус r:

Площадь круга: -

Определение основных понятий

Прежде чем погрузиться в последовательность расчетов и узнать, чему равна площадь круга, важно выяснить разницу между понятиями окружности и круга.

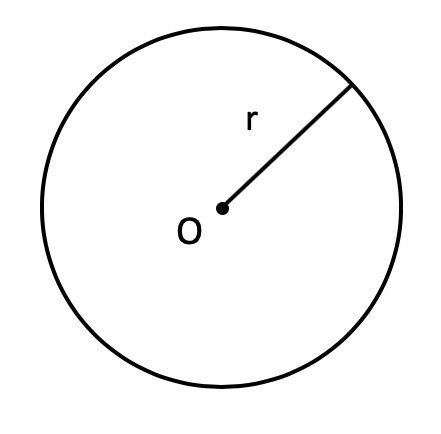
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.

Если говорить простым языком, окружность — это замкнутая линия, как, например, кольцо и шина. Круг — плоская фигура, ограниченная окружностью, как монетка или крышка люка.

214.3K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

Подготовься к ОГЭ на пятёрку
Подготовься к ЕГЭ на высокие баллы
Записывайся на бесплатные курсы для детей
Решай задания в бесплатном тренажёре ЕГЭ

Формула вычисления площади круга

Давайте разберем несколько формул расчета площади круга. Поехали!

Площадь круга через радиус

S = π × r², где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.

радиус круга

Площадь круга через диаметр

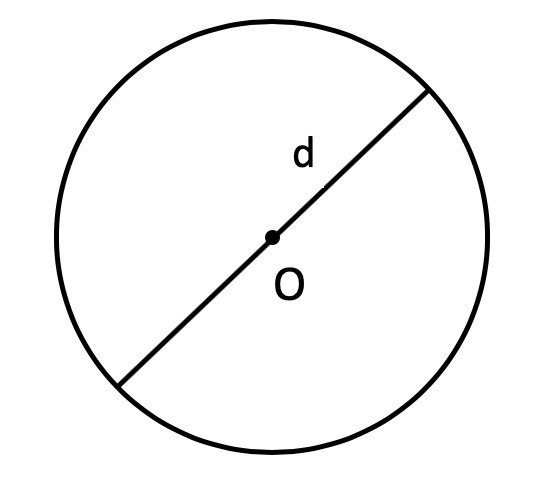
S = d² : 4 × π, где d — это диаметр.

диаметр круга

Площадь круга через длину окружности

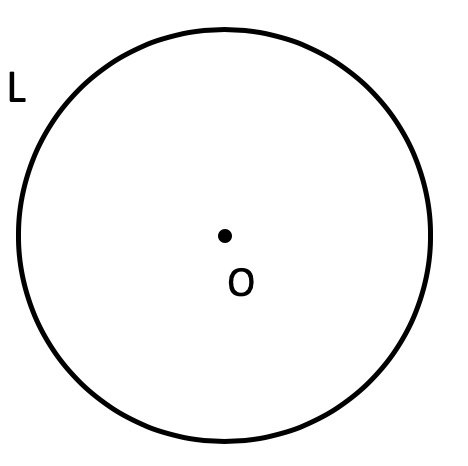
S = L² : (4 × π), где L — это длина окружности.

длина окружности

Важно!

Задачку не решить, если длина и ширина даны в разных единицах. Для правильного решения переведите все данные к одной единице измерения, и все получится.

Популярные единицы измерения площади:

квадратный миллиметр (мм²);
квадратный сантиметр (см²);
квадратный дециметр (дм²);
квадратный метр (м²);
квадратный километр (км²);
гектар (га).

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Задачи. Определить площадь круга

Мы разобрали три формулы для вычисления площади круга. А теперь тренироваться — поехали!

Задание 1. Как найти площадь круга по диаметру, если значение радиуса равно 6 см.

Как решаем:

Диаметр окружности равен двум радиусам.
Используем формулу: S = π × d² : 4.
Подставим известные значения: S = 3,14 × 12² : 4.

S = 113,04 см².

Ответ: 113,04 см².

Задание 2. Найти площадь круга, если известен диаметр, равный 90 мм.

Как решаем:

Используем формулу: S = π × d² : 4.
Подставим известные значения: S = 3,14 × 90² : 4.

S = 6358,5 мм².

Ответ: 6358,5 мм².

Задание 3. Найти длину окружности при радиусе 3 см.

Как решаем:

Отношение длины окружности к диаметру является постоянным числом.

π = L : d
Получается: L = d × π.
Так как диаметр равен двум радиусам, то формула длины окружности примет вид: L = 2 × π × r.
Подставим значение радиуса: L = 2 × 3,14 × 3.

L = 18,84 см².

Ответ: 18,84 см².