Прямые параллельны, если они лежат в одной плоскости и не пересекаются. Также, если при пересечении секущей образуются равные накрест лежащие углы. Например,
- две прямые a и b,
- пересеченные секущей в точках A и B,
- образуют равные углы 1 и 2,
- значит они параллельны.
Для кого эта статья:
- Студенты и школьники, изучающие геометрию
- Преподаватели математики, желающие использовать статью в учебном процессе
- Все, интересующиеся основами евклидовой геометрии
Определение параллельности прямых
Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.
|
Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b. |
Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.
Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.
|
На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна. |
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Свойства и признаки параллельных прямых
Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.
Свойства параллельных прямых:
- Если одна из прямых параллельна третьей, то и другая прямая параллельна третьей.
- Если прямая пересекает одну из параллельных прямых, то она пересекает и вторую.
- Углы, образованные пересечением параллельных прямых с третей прямой, равны.
- Сумма внутренних углов, находящихся на одной стороне от пересекающей прямой, составляет 180 градусов.
Примеры:
- Прямые a и b параллельны, и третья прямая c пересекает их, образуя углы 70° и 110°.
- Если a || b и c || b, то a || c.
Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.
Если секущая проходит через две параллельные прямые, то:
- два внутренних односторонних угла образуют в сумме 180°:
∠4 + ∠5 = 180°; ∠3 + ∠6 = 180°.
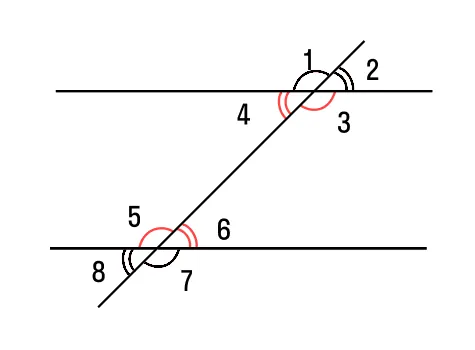
- два внутренних накрест лежащих угла равны между собой:
∠3 = ∠5, ∠4 = ∠6.

- два соответственных угла равны между собой:
∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.
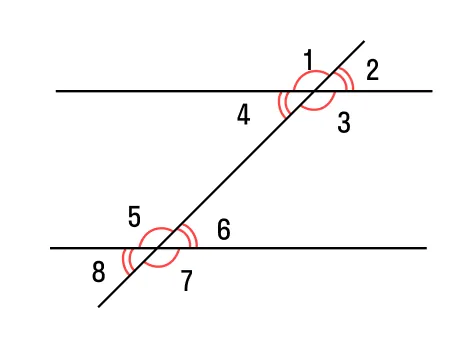
|
Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой. |

Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.
Признаки параллельности двух прямых - это условия, при выполнении которых две прямые считаются параллельными. Примеры признаков:
- Если накрест лежащие углы равны при пересечении прямых секущей.
- Если соответствующие углы равны.
- Если сумма односторонних углов равна 180°.
А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.
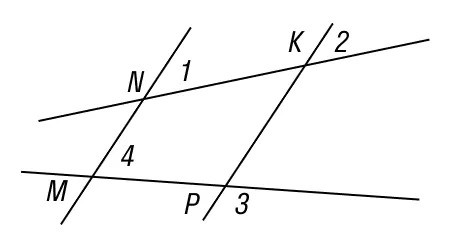
Задача 1
Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.
Решение
В данном случае ∠3 и ∠MPK являются вертикальными, следовательно ∠MPK = ∠3 = 92°.
Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP.
Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.
∠4 = 180° - 92° = 88°
Задача 2
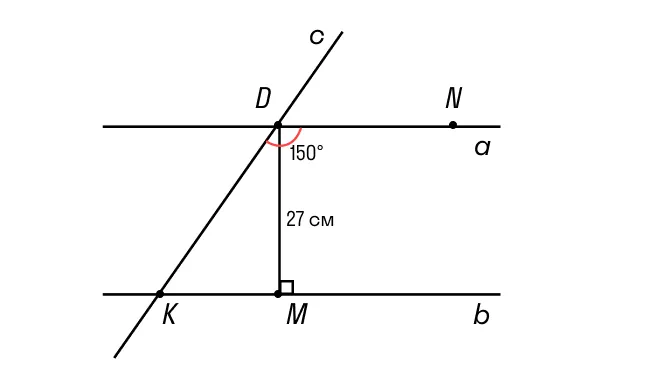
Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.
Решение
Поскольку а II b, значит ∠MKD + ∠KDN = 180°.
Соответственно, ∠MKD = 180° - ∠KDN = 180° - 150° = 30°.
Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.
Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.
DK = 2DM = 2 х 27 = 54 (см)