Как найти косинус: косинус угла в прямоугольном треугольнике определяется как отношение прилежащего катета к гипотенузе. Например, в треугольнике (ABC), где
Формулировка и доказательство теоремы косинусов
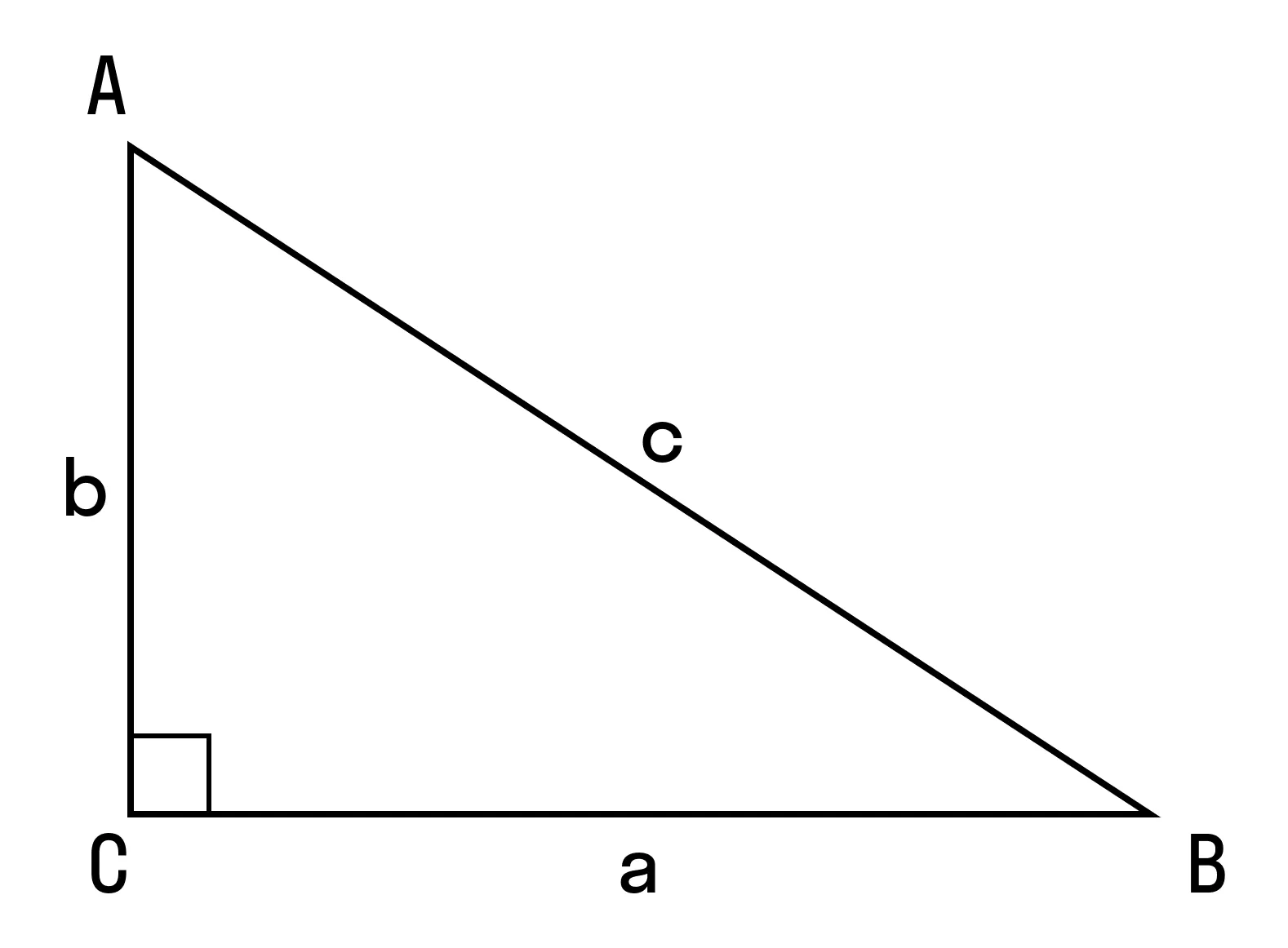
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a2> + b2> = c2>, где a, b — катеты, с — гипотенуза.
|
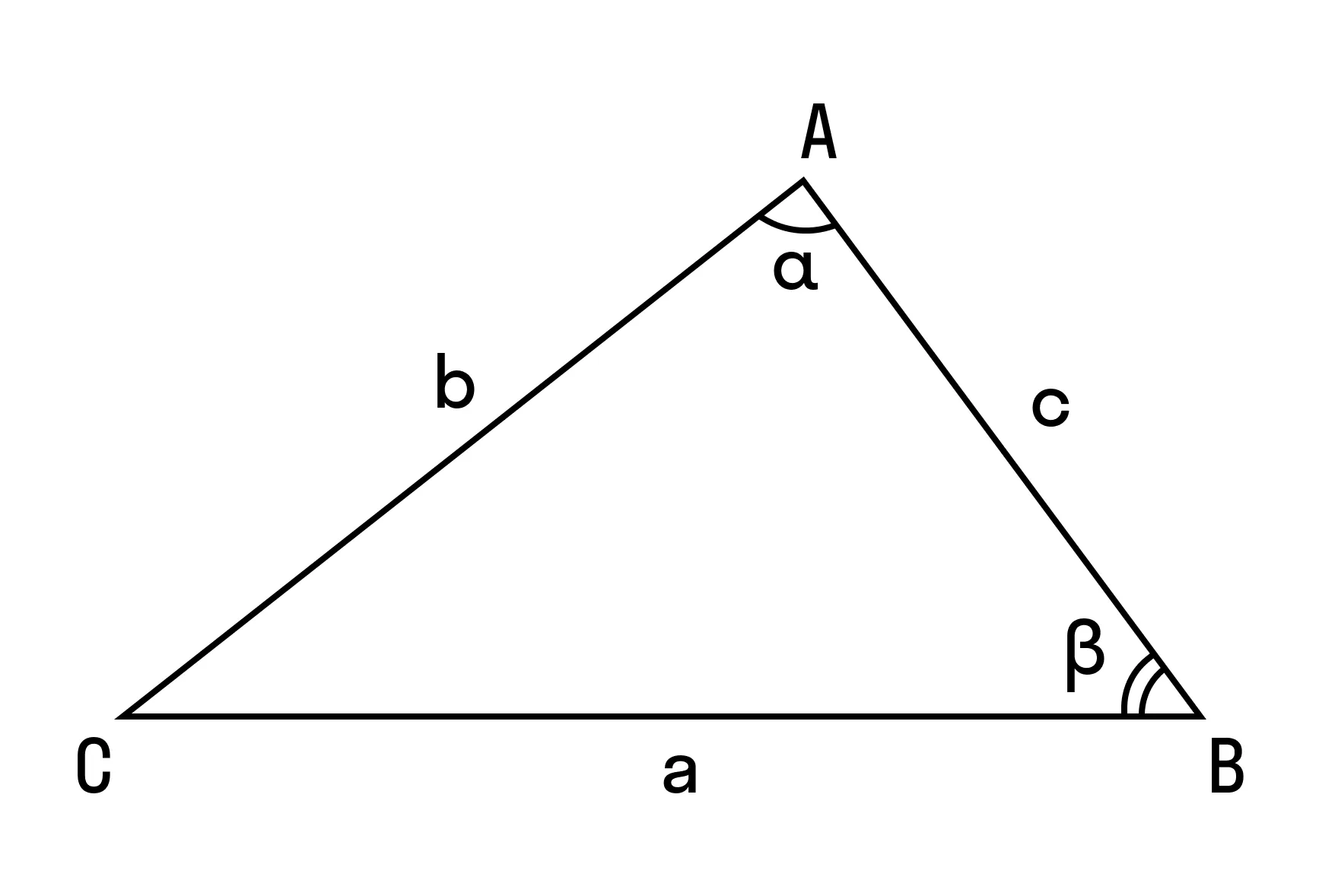
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними. Формула теоремы косинусов: a2 = b2 + c2 - 2bc cos α |
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
BC2 = (x2 - x1)2 + (y2 - y1)2
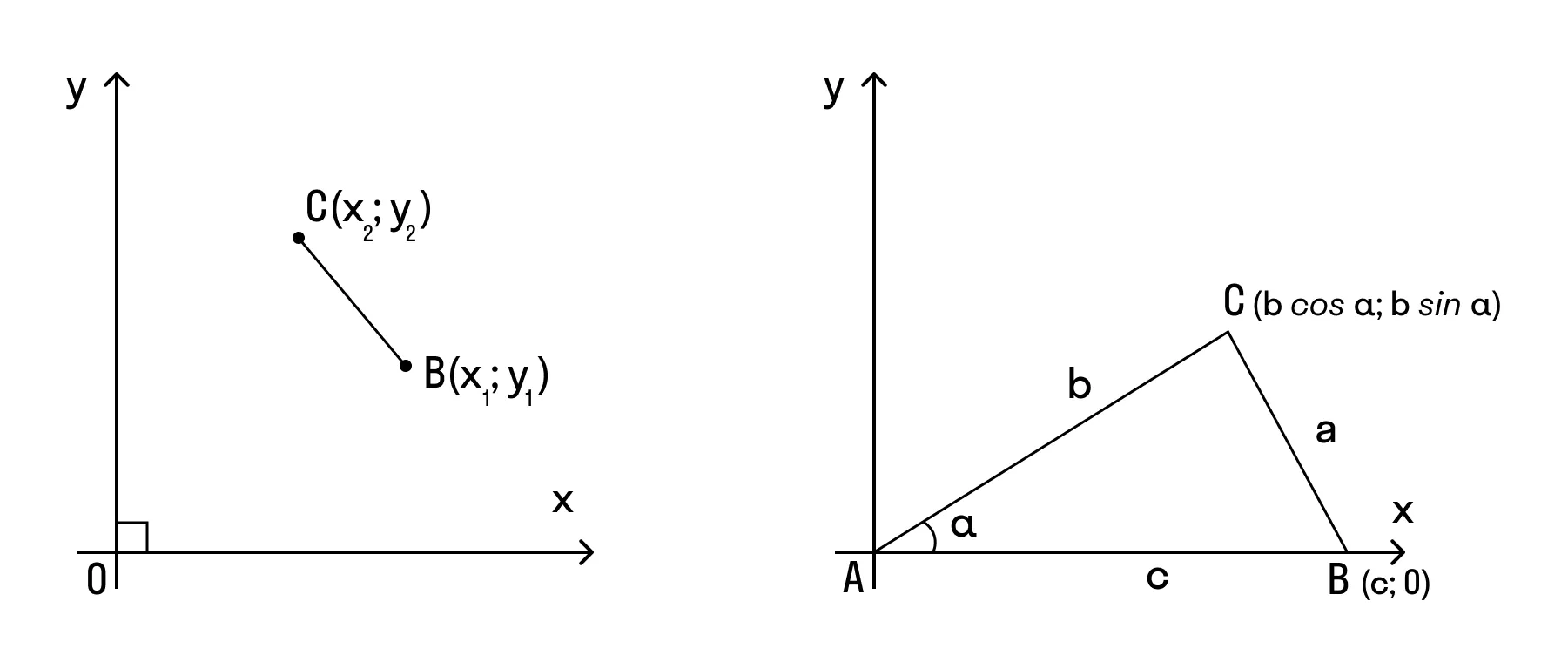
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
cos2α + sin2α = 1 — основное тригонометрическое тождество.
BC2 = a2 = (b cos α - c)2 + b2sin2α = b2cos2α + b2sin2α - 2bc cos α + c2 = b2(cos2α + sin2α) - 2bc cos α + c2
Что и требовалось доказать.
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
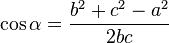
- Когда b2 + c2 - a2 > 0, угол α будет острым.
- Когда b2 + c2 - a2 = 0, угол α будет прямым.
- Когда b2 + c2 - a2 < 0, угол α будет тупым.
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b × cos α,
- DB = c – b × cos α.
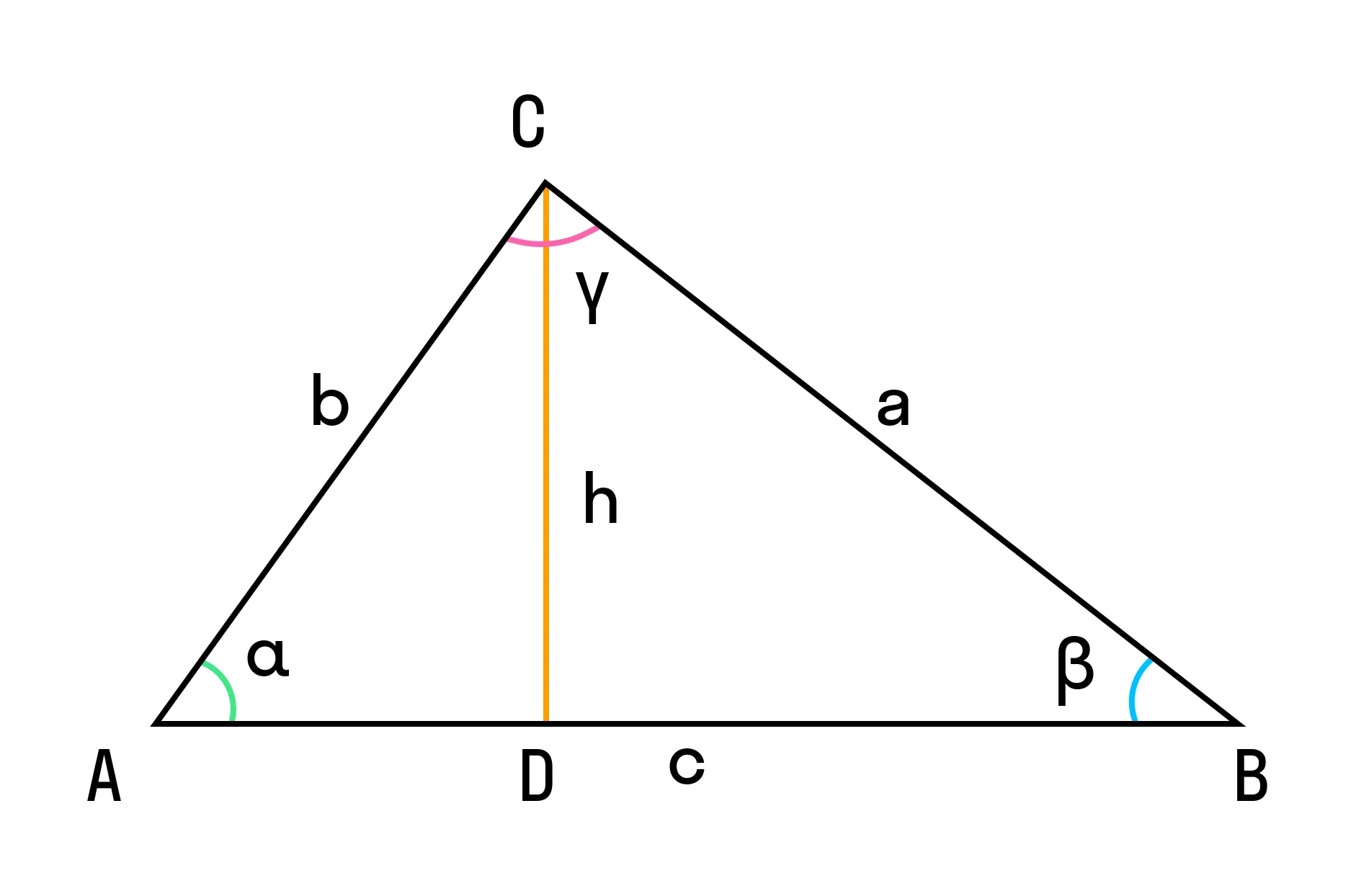
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h2 = b2 - (b × cos α)2
- h2 = a2 - (c – b × cos α)2
Приравниваем правые части уравнений:
- b2 - (b × cos α)2 = a2 - (c - b × cos α)2
либо
- a2 = b2 + c2 - 2bc × cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
- b2 = a2 + c2 - 2ac × cos β;
- c2 = a2 + b2 - 2ab × cos γ.
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a2 = b2 + c2 - 2bc cos α
b2 = c2 + a2 - 2ca cos β
c2 = a2 + b2 - 2ab cos γ
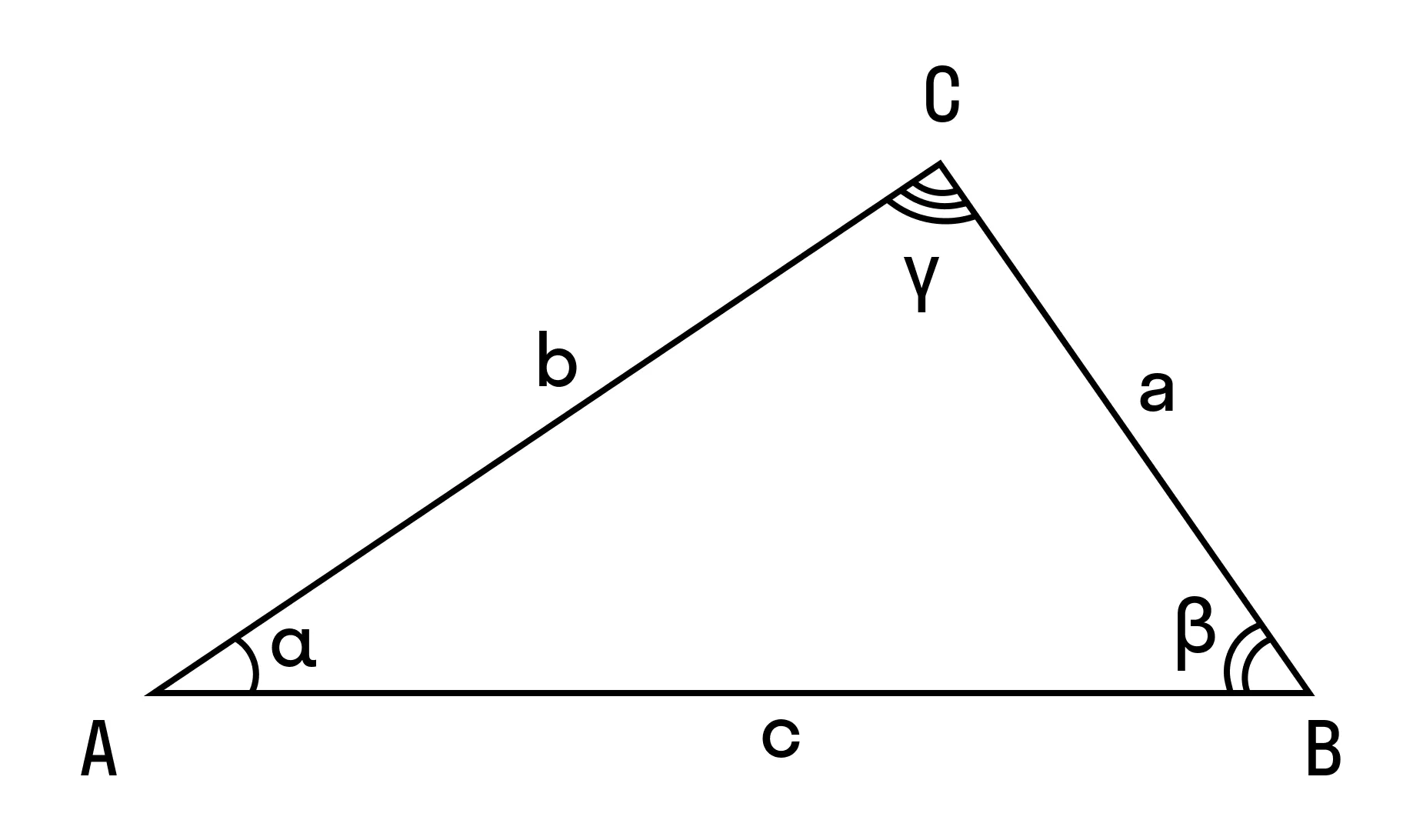
Теорема косинусов может быть использована для любого вида треугольника.
Получи больше пользы от Skysmart:
-
Подготовься к ОГЭ на пятёрку.
-
Подготовься к ЕГЭ на высокие баллы.
Записывайся на бесплатные курсы для детей.
Решай задания в бесплатном тренажёре ЕГЭ.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
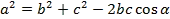
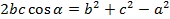
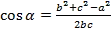
Аналогично:
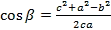
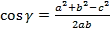
Определение угла с помощью косинуса
Косинус угла - это тригонометрическая функция, равная отношению длины прилежащего катета к длине гипотенузы в прямоугольном треугольнике. Например, для угла 30° косинус равен 0.866, а для угла 60° - 0.5.
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
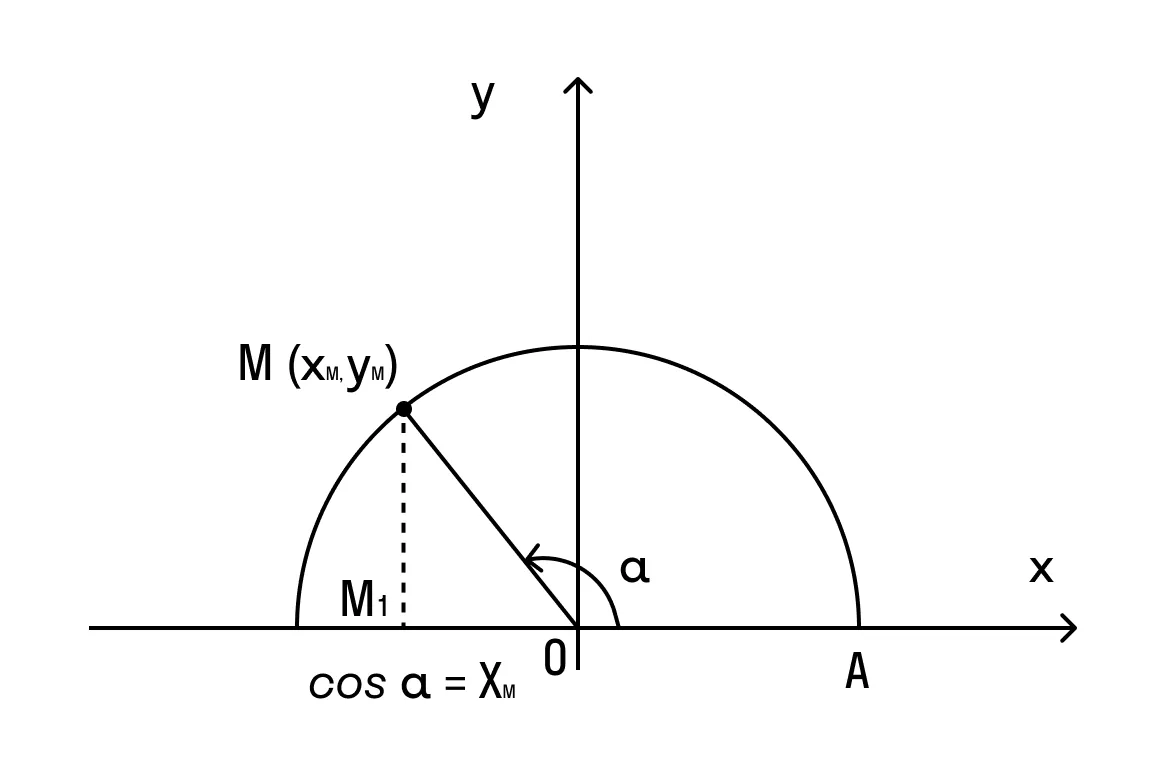
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 < cos α < 1.
Предел изменения синуса: 0 < sin α ≤ 1.
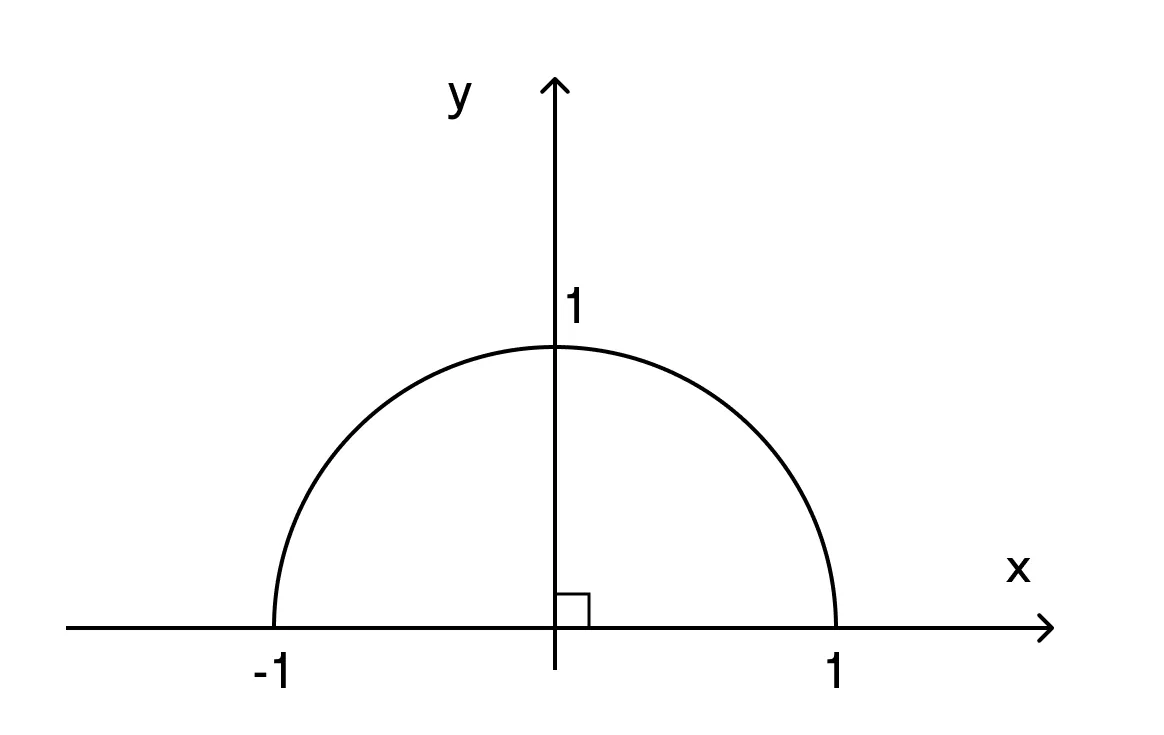
- Если cos α > 0, то α ∈ (0°;90°)
- Если cos α < 0, то α ∈ (90°;180°)
- Если cos α = 0, то α = 90°
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
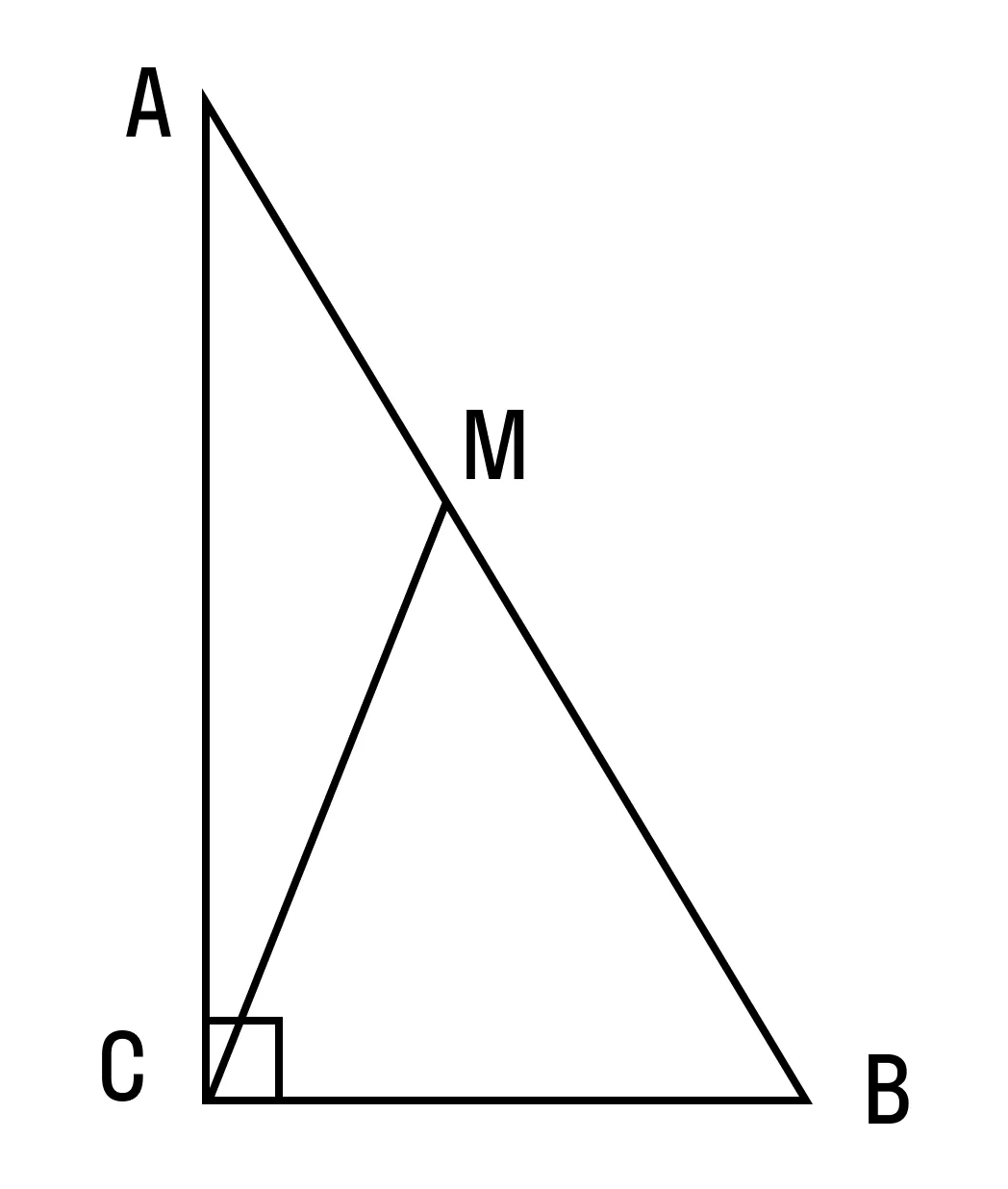
Как решаем:
- Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:
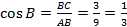
- Из треугольника СМВ по теореме косинусов найдём СМ:
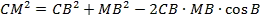
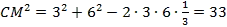
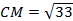
Ответ: СМ =
Пример 2. Дан треугольник АВС, в котором a2 + b2 < c2. Доказать, что ∠C — тупой угол.
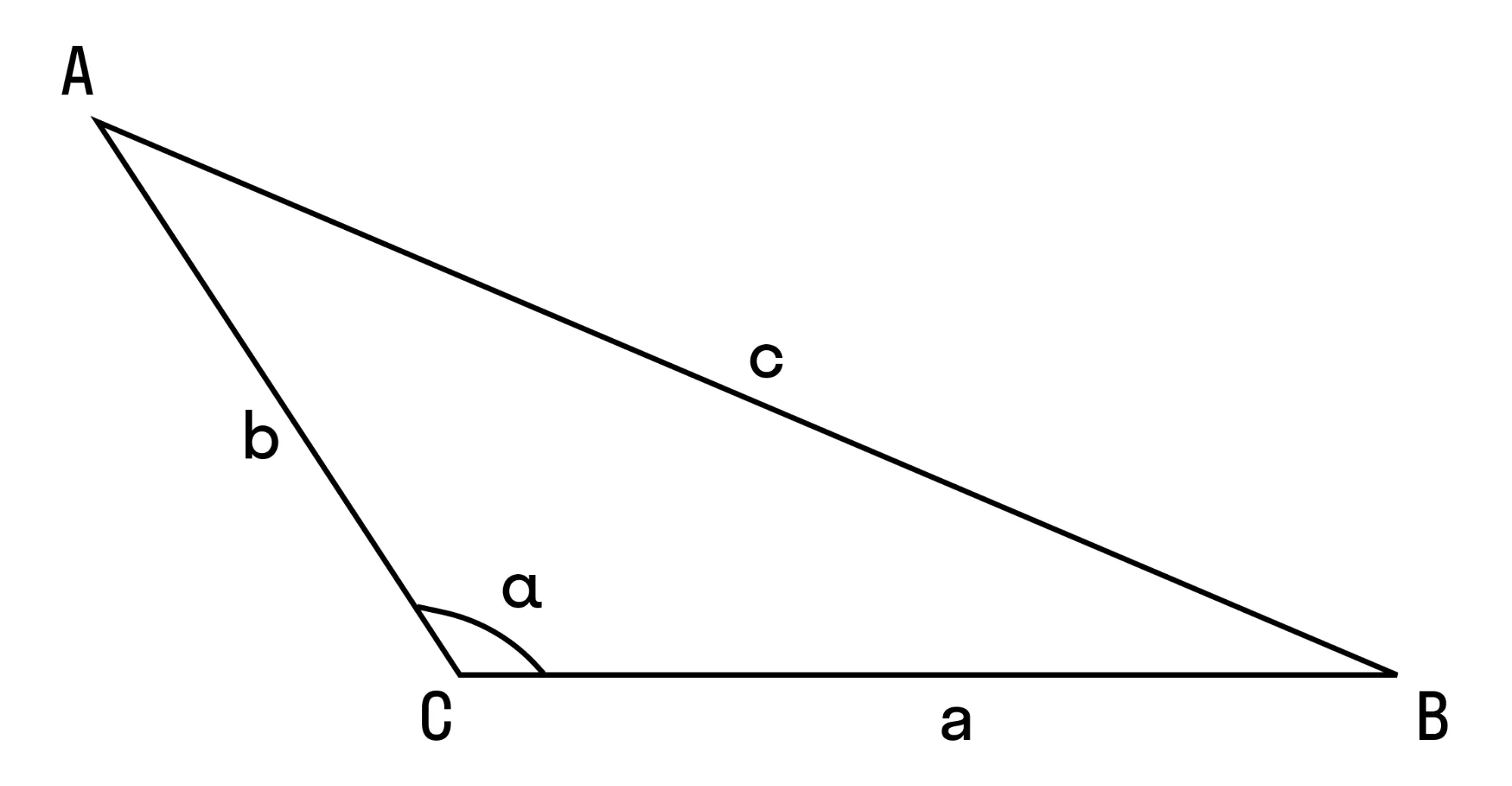
Как доказываем:
- Для доказательства нужно вспомнить теорему косинусов для угла ∠C:
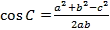
- Так как a2 + b2 < c2, то cos C < 0, следовательно, ∠C — тупой.
Что и требовалось доказать.
Эта задача нам показала, что с помощью теоремы косинусов можно определить тупой угол или острый.
- Если c2 = a2 + b2, то ∠C = 90°.
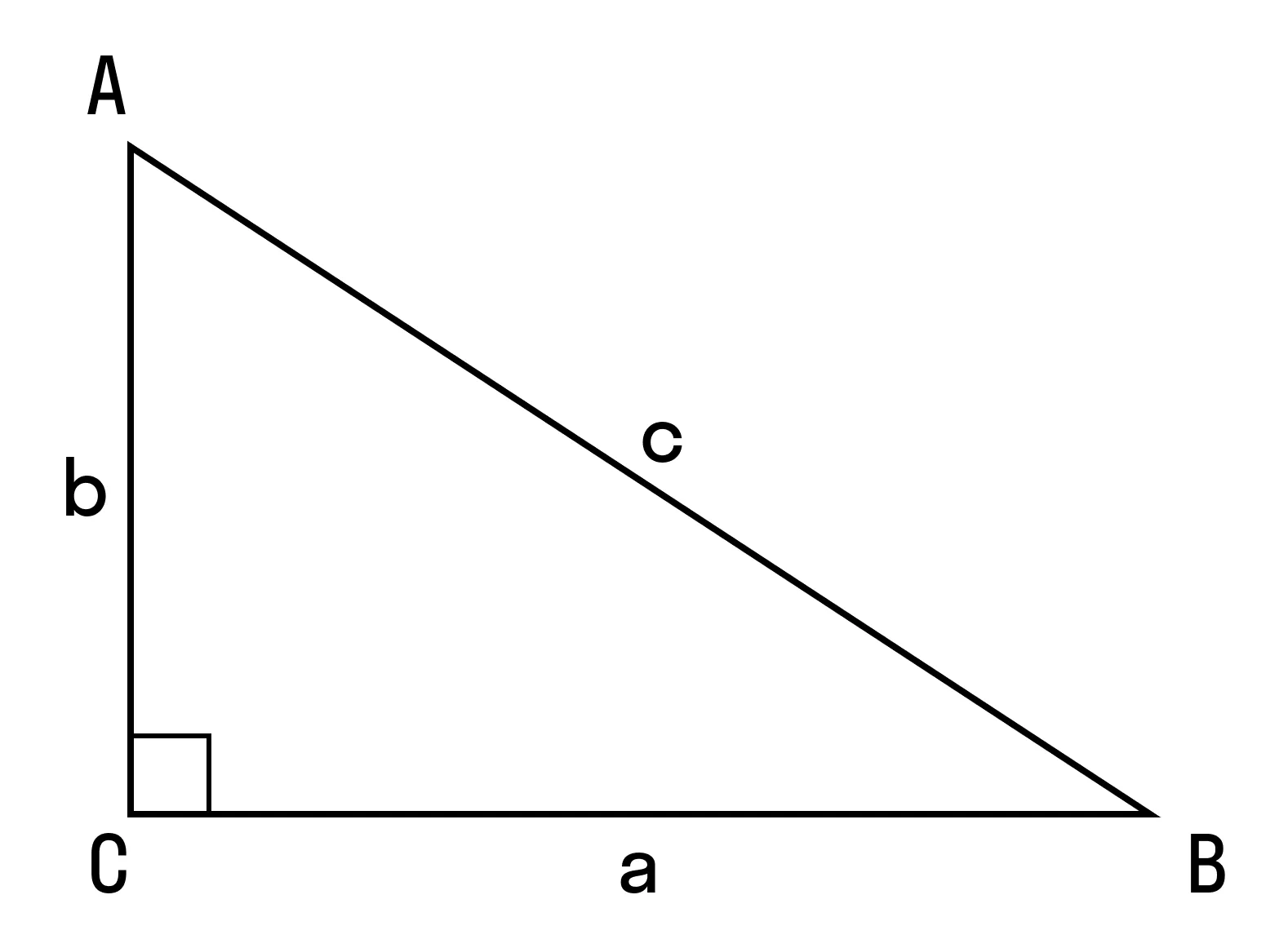
- Если c2 < a2 + b2, то ∠C — острый.
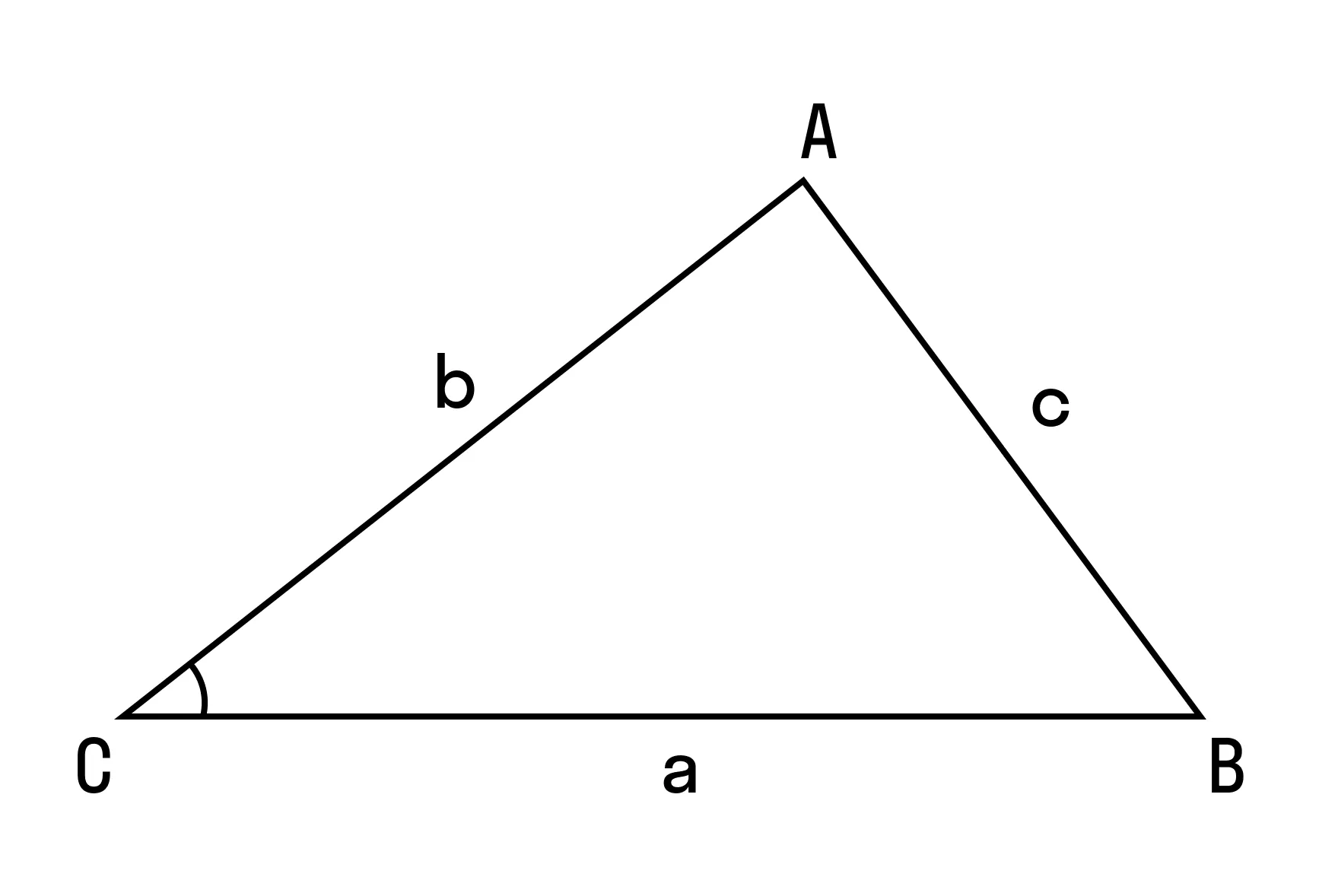
Больше объяснений по этой и другим темам вы найдете в справочнике по математике — с формулами, чертежами и примерами решения задач.
