Трапеция: формулы и свойства

Определение трапеции и её элементы

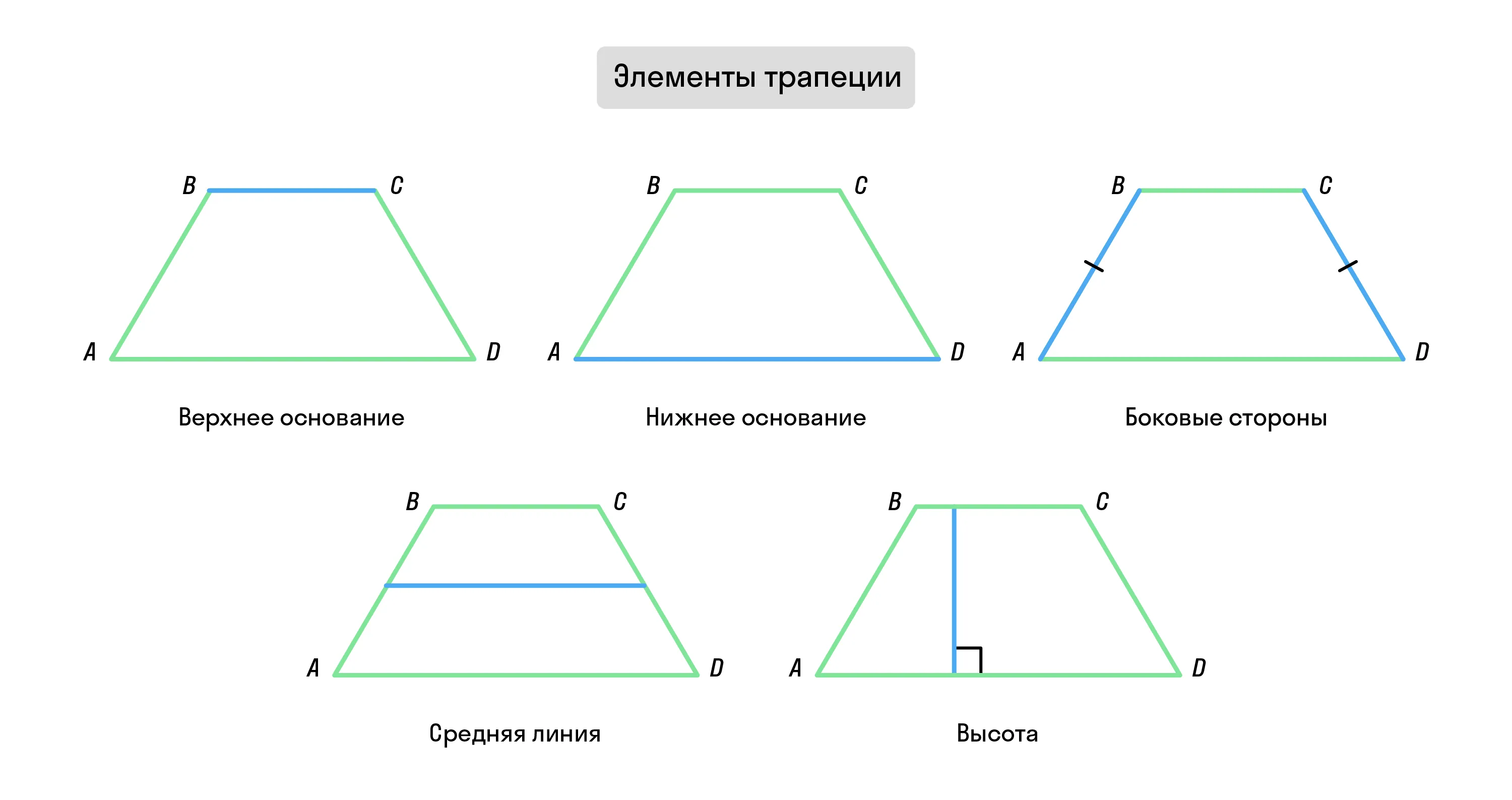
Трапеция — это четырёхугольник, только две стороны которого параллельны.

Параллельные стороны трапеции называются основаниями (верхнее, как правило, меньшее, а нижнее — большее). Две другие стороны, не параллельные друг другу, принято называть боковыми.

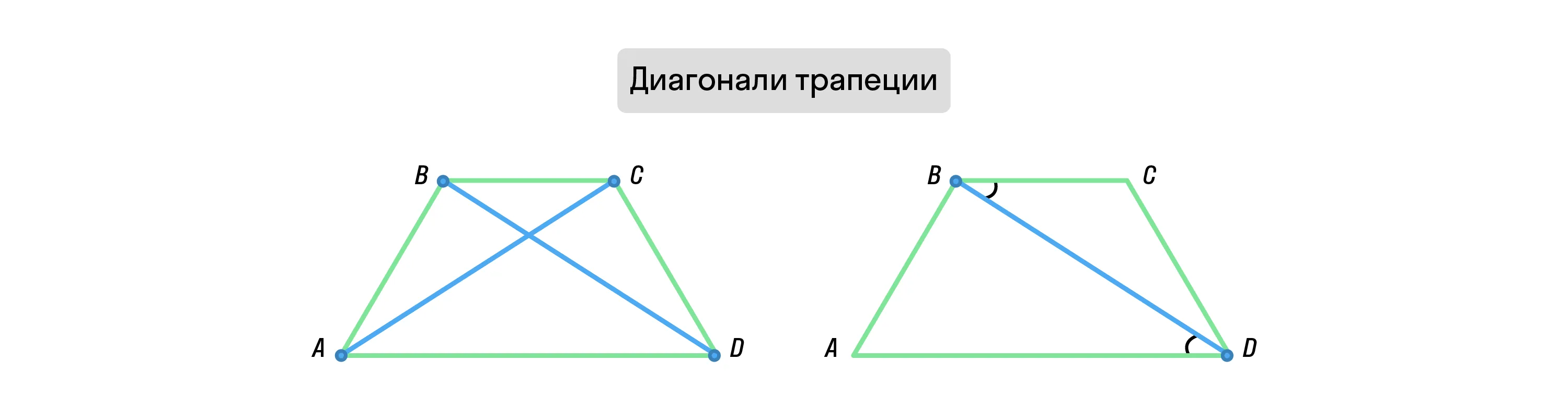
В трапеции можно провести две диагонали.

Обратите внимание

На рисунке угол CBD и угол ADB отмечены равными. Можете ли вы объяснить, почему это верно?

Так как в трапеции основания параллельны по определению, диагональ BD можно считать секущей. И тогда указанные выше углы равны, так как являются накрест лежащими. Аналогично для диагонали АС: угол ВСА и угол CAD равны.

Знания по темам «Параллельные прямые» и «Секущая» часто применяются в решении задач про трапецию. Если эта тема у вас вызывает затруднения, приходите на курсы по математике в онлайн-школу Skysmart: на них вы закрепите эту и другие темы из школьной программы, а также подготовитесь к ЕГЭ или ОГЭ за короткий срок.

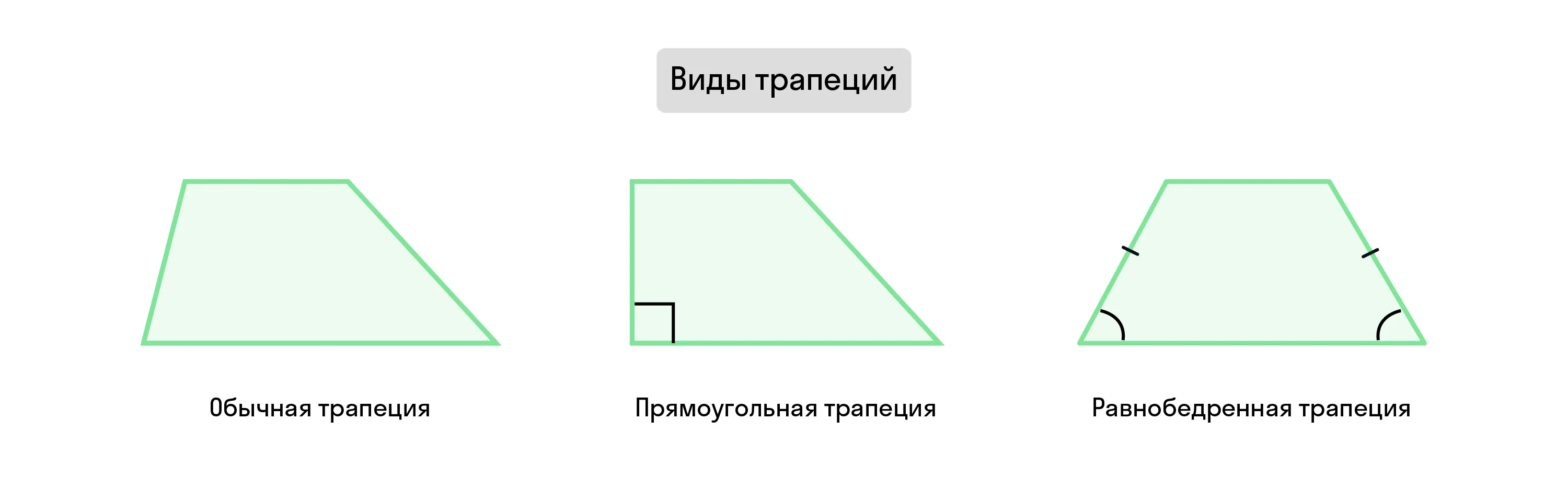
Виды трапеций

Вышеперечисленные элементы есть у всех трапеций без исключений. А по виду трапеции делятся на:

• обычные,

• равнобедренные или равнобокие — у них равны боковые стороны и углы при основании,

• прямоугольные, у которых один из углов при основании равен 90°, т. е. одна из боковых сторон перпендикулярна основаниям трапеции.

169.9K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Средняя линия трапеции

Средняя линия трапеции — отрезок, соединяющий середины боковых сторон и параллельный основаниям трапеции. Чаще всего среднюю линию обозначают буквами MN, но это не является правилом.

Средняя линия равна полусумме оснований трапеции.

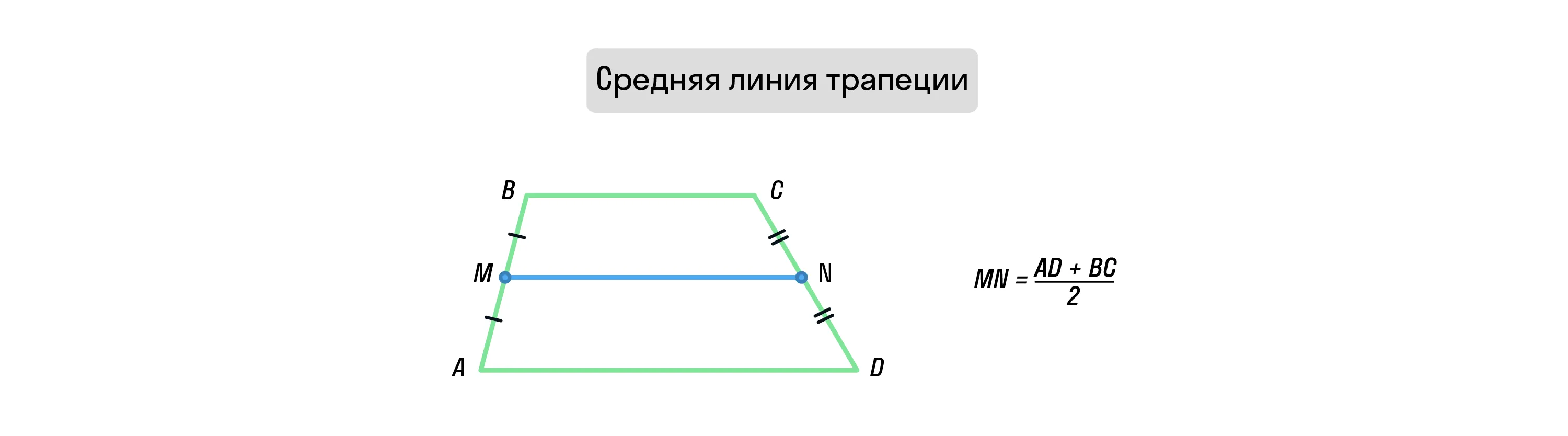
Длины оснований и средней линии трапеции составляют арифметическую прогрессию. То есть верхнее основание отличается от средней линии на столько же, на сколько средняя линия отличается от нижнего основания.

Например: если BC = 5 и AD = 13, то MN = (5 + 13) / 2 = 9.

Ряд чисел {5; 9; 13} — арифметическая прогрессия, в которой разница между соседними элементами равна 4.

Диагонали делят среднюю линию трапеции на три отрезка. Средний из них равен полуразности оснований, а два крайних равны между собой:

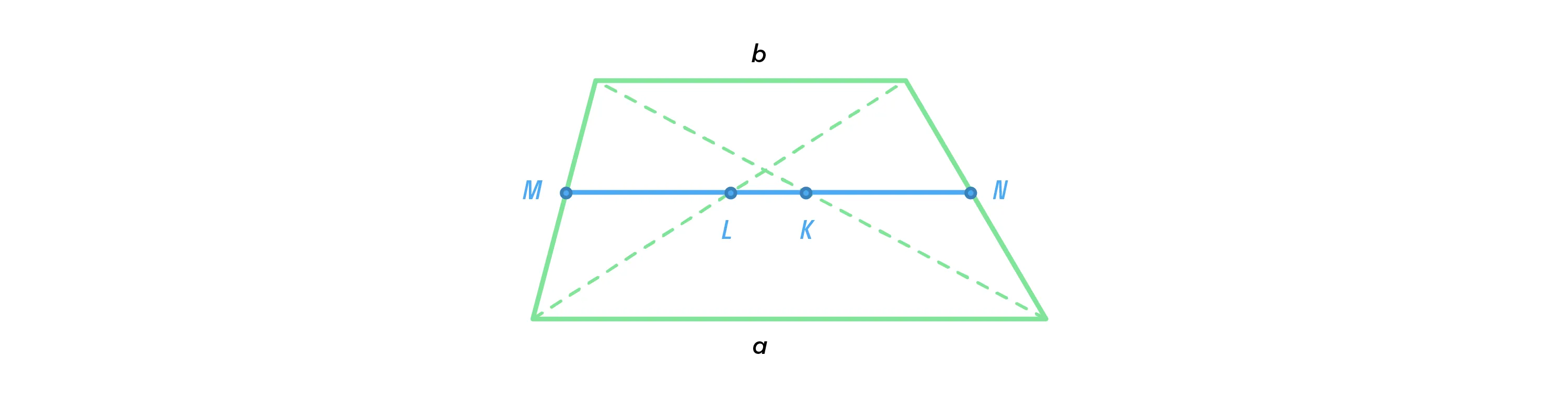
А как найти отрезки МL и KN?
Они равны половине верхнего основания, , так как являются средними линиями для треугольников, отсекаемых соответственными диагоналями.

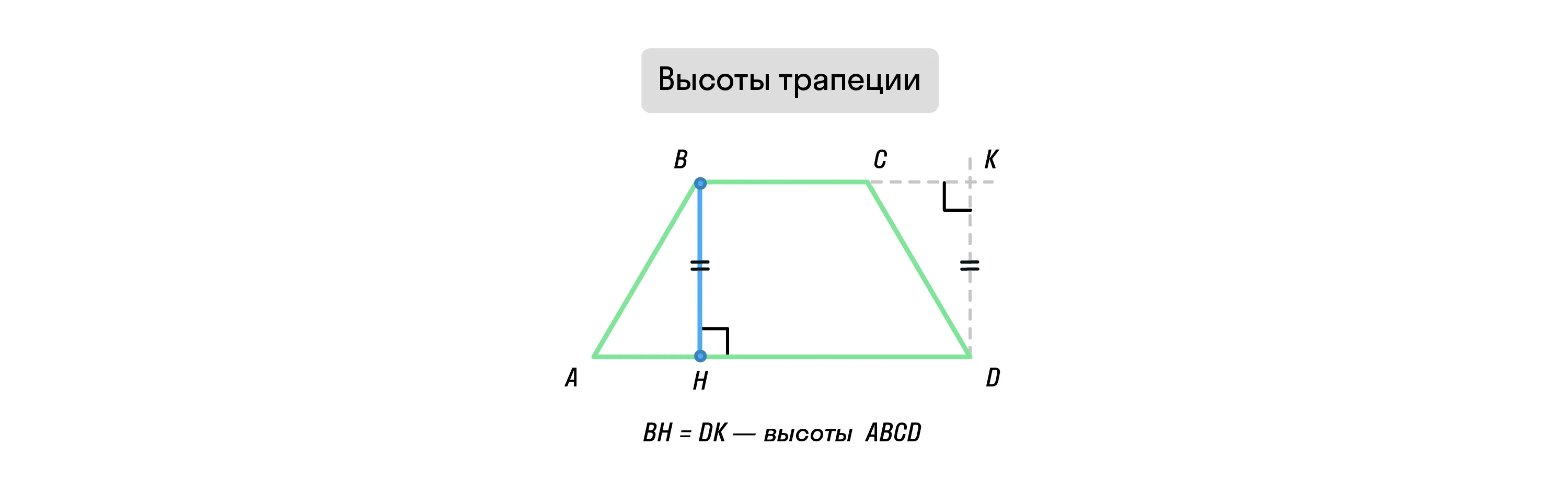
Высота трапеции

Высота трапеции — это перпендикуляр, проведенный из вершины угла трапеции на прямую, содержащую противолежащее основание. Из какого бы угла мы ни провели высоты, они будут равны друг другу. А в прямоугольной трапеции высота совпадает с одной из боковых сторон!

Площадь и периметр трапеции

Периметр трапеции — сумма длин всех её сторон.

Площадь трапеции можно вычислить по формуле:

, где:

• a, b — основания трапеции;

• h — высота трапеции;

• MN — средняя линия трапеции.

Также можно воспользоваться дополнительными формулами:

, где:

• d₁, d₂ — диагонали трапеции;

• — синус острого угла между ними.

, где:

• p — полупериметр трапеции;

• r — радиус вписанной окружности.

Не забывайте, что площадь любой фигуры также можно найти через сумму площадей фигур, которые её составляют. Например, если в трапеции проведены диагонали, делящие её на четыре треугольника, то площадь трапеции будет равна сумме площадей этих треугольников.

Вписанная и описанная трапеции

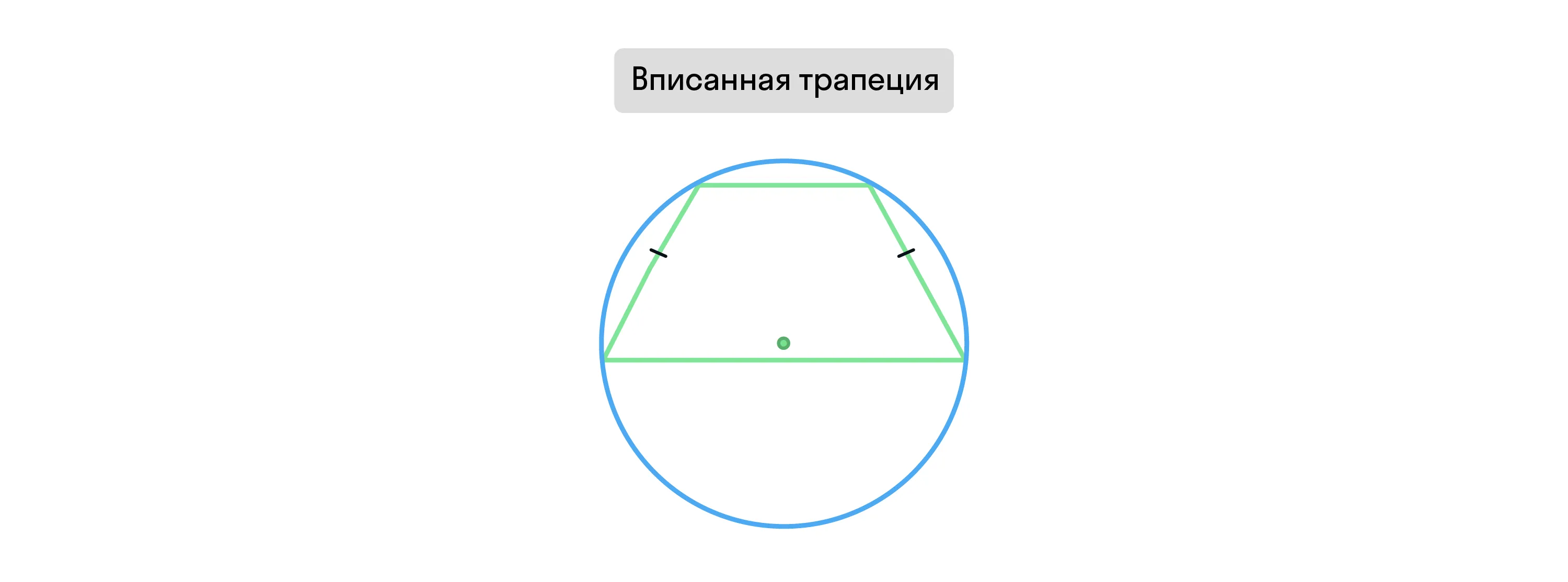
Если трапеция вписана в окружность, то она равнобедренная. И наоборот, если трапеция равнобедренная, то около неё можно описать окружность.

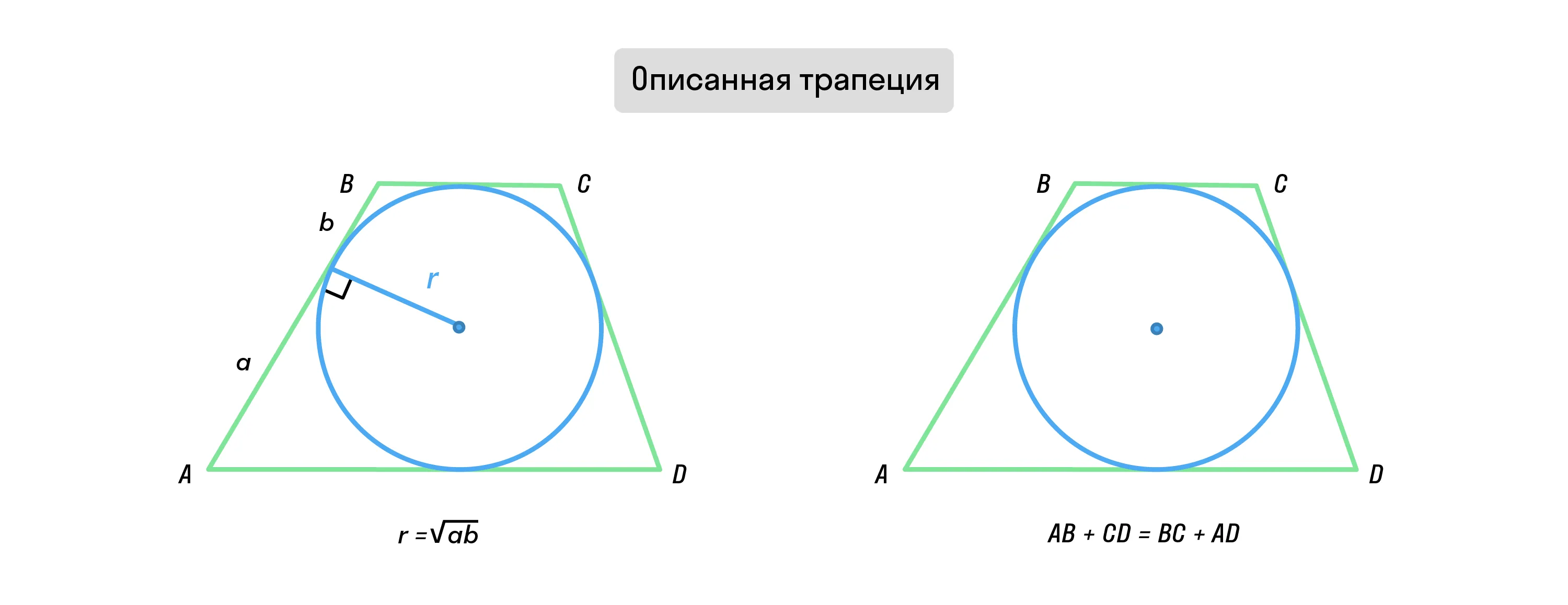
1. Если трапеция описана около окружности, то сумма оснований трапеции равна сумме её боковых сторон.

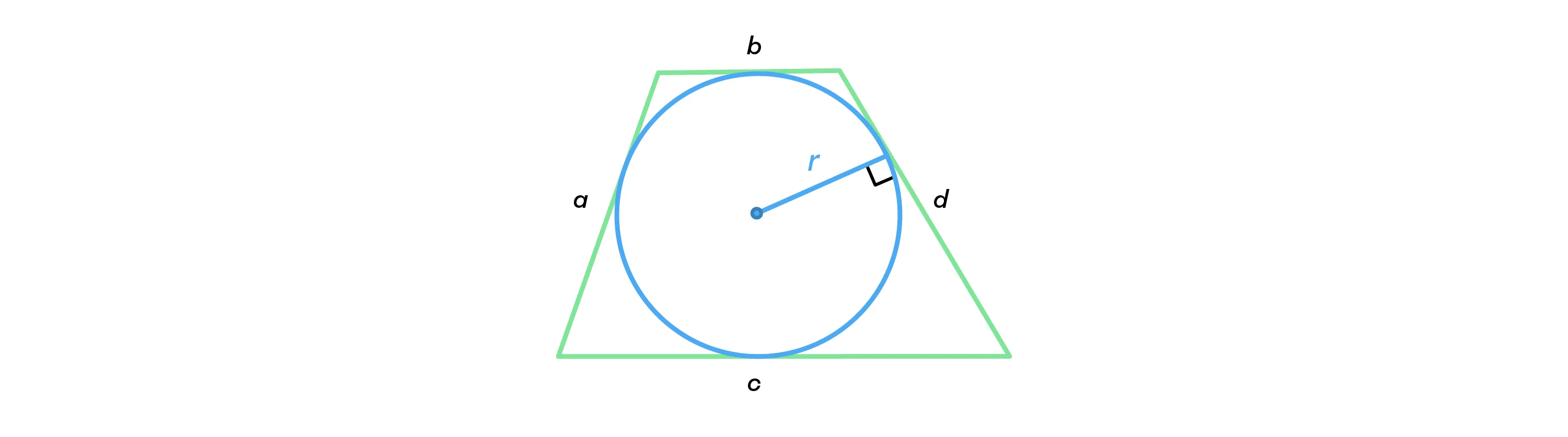
2. Если в трапецию вписана окружность с радиусом r и она делит боковую сторону точкой касания на два отрезка — a и b, то .

3. Радиус вписанной окружной также можно найти через формулу , где h — высота трапеции.

Свойства трапеции

Основные свойства

Как у любой другой геометрической фигуры, у трапеции есть определённые свойства или характеристики, которые являются для неё отличительными, выделяют из списка фигур.

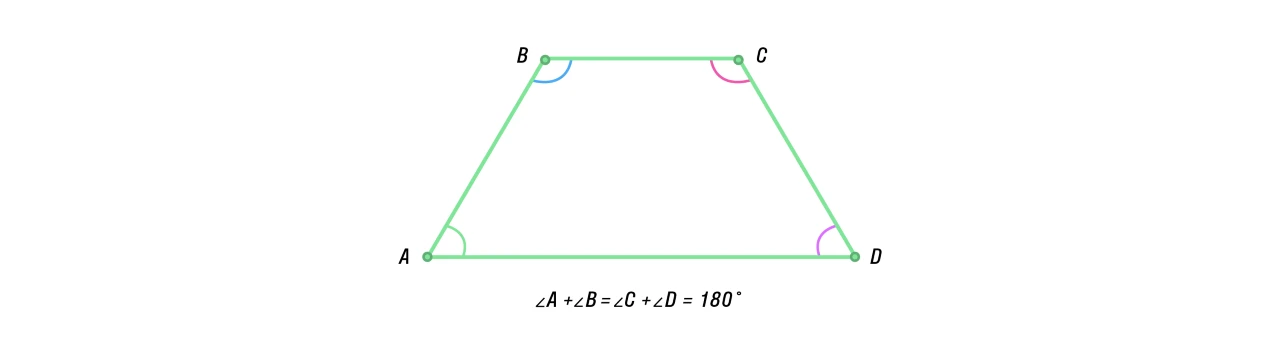
1. Для трапеции справедливо свойство любого четырёхугольника: сумма её углов равна 360°.

2. Сумма углов, прилежащих к боковой стороне трапеции, равна 180°.

   

3. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

   

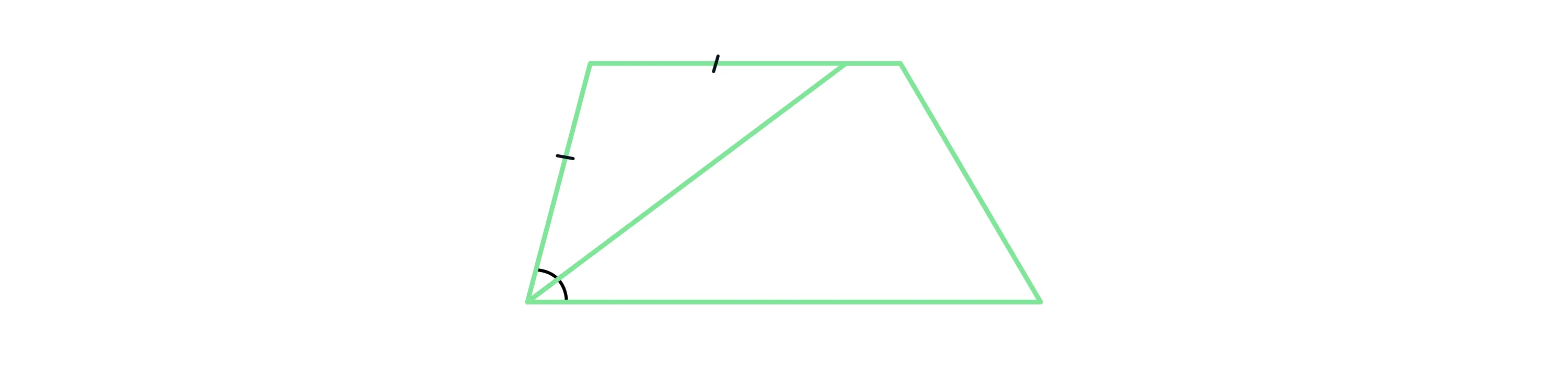
4. Треугольники AOD и COB, образованные при пересечении диагоналей, подобны: k = AD/BC.

   

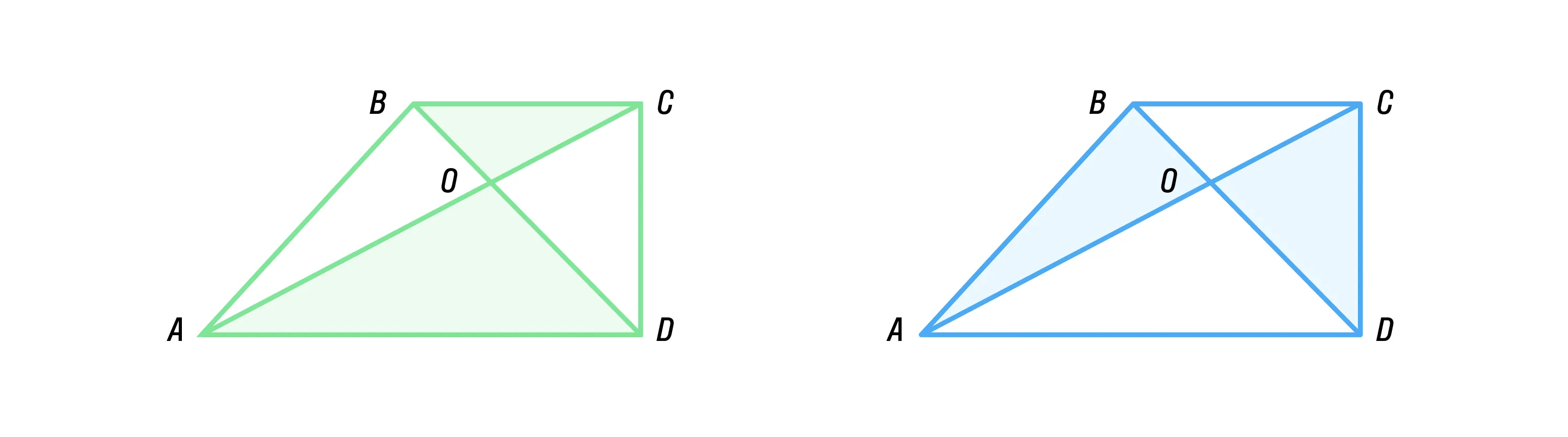
   Треугольники ABO и DCO имеют одинаковую площадь, т. е. они равновеликие.

5. «Замечательное свойство трапеции»: точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

   

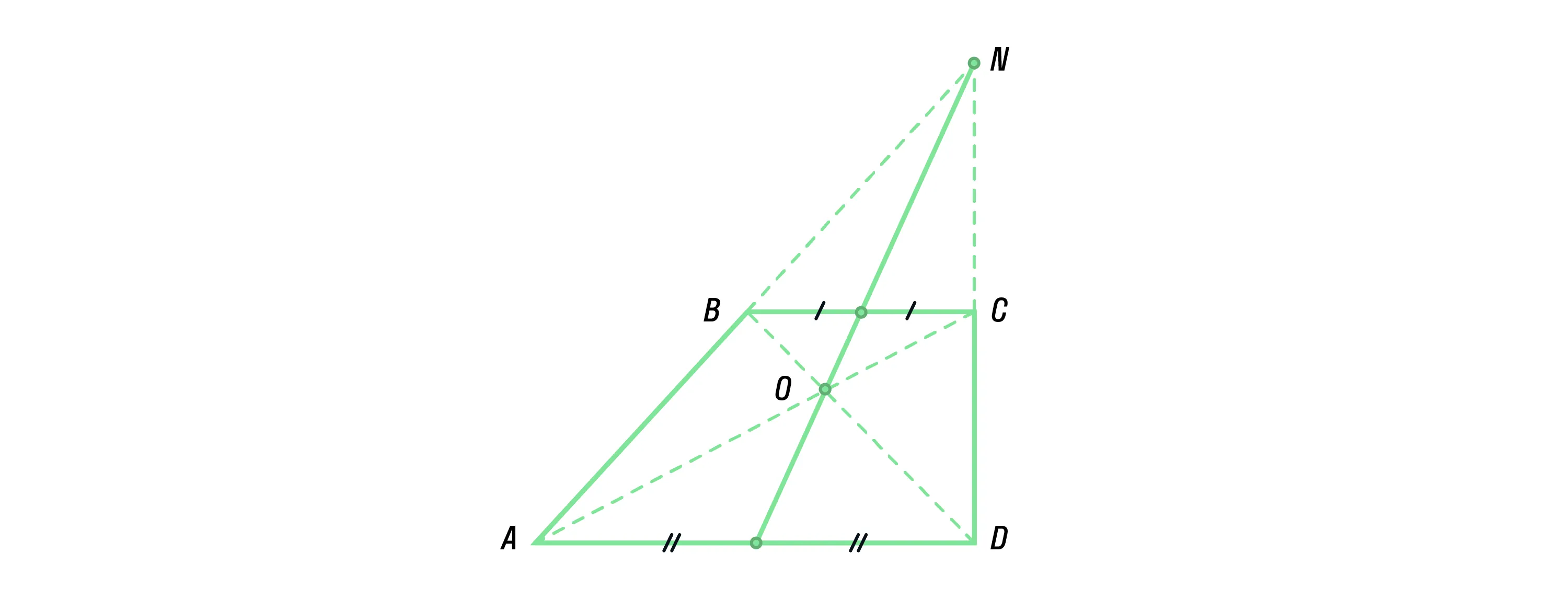
6. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

   

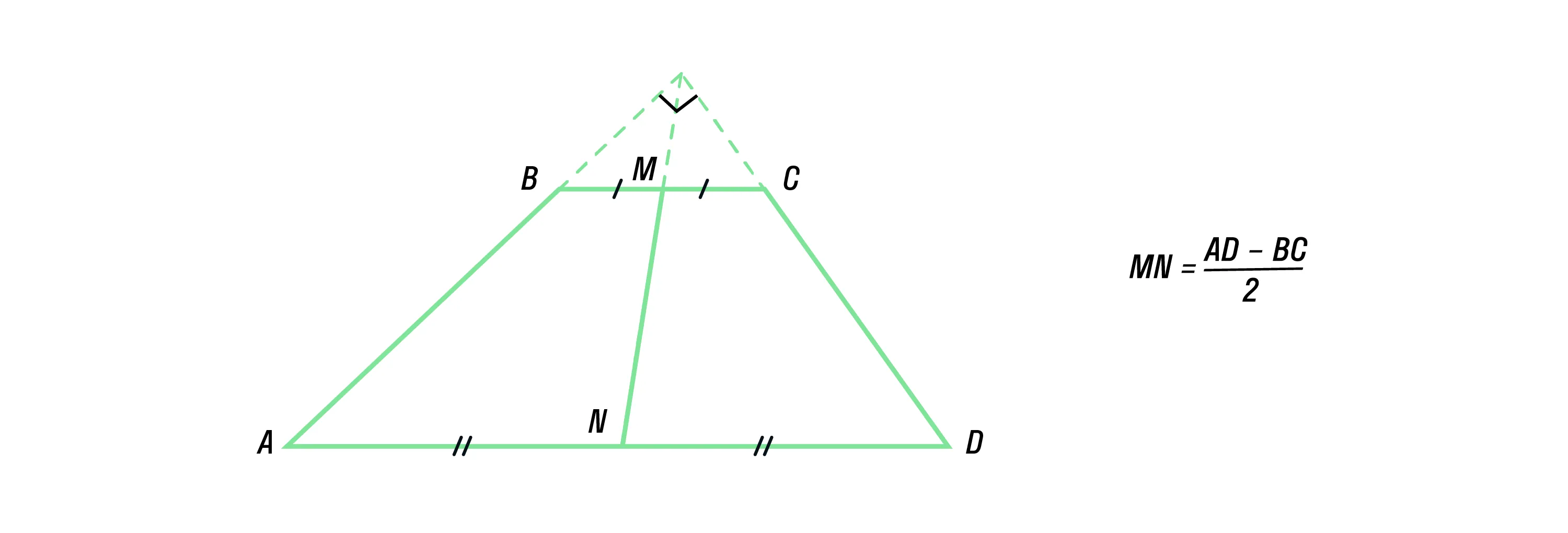
Свойства равнобедренных трапеций

Отдельно можно выделить дополнительные свойства равнобедренных трапеций:

1. Диагонали в равнобедренной трапеции равны.

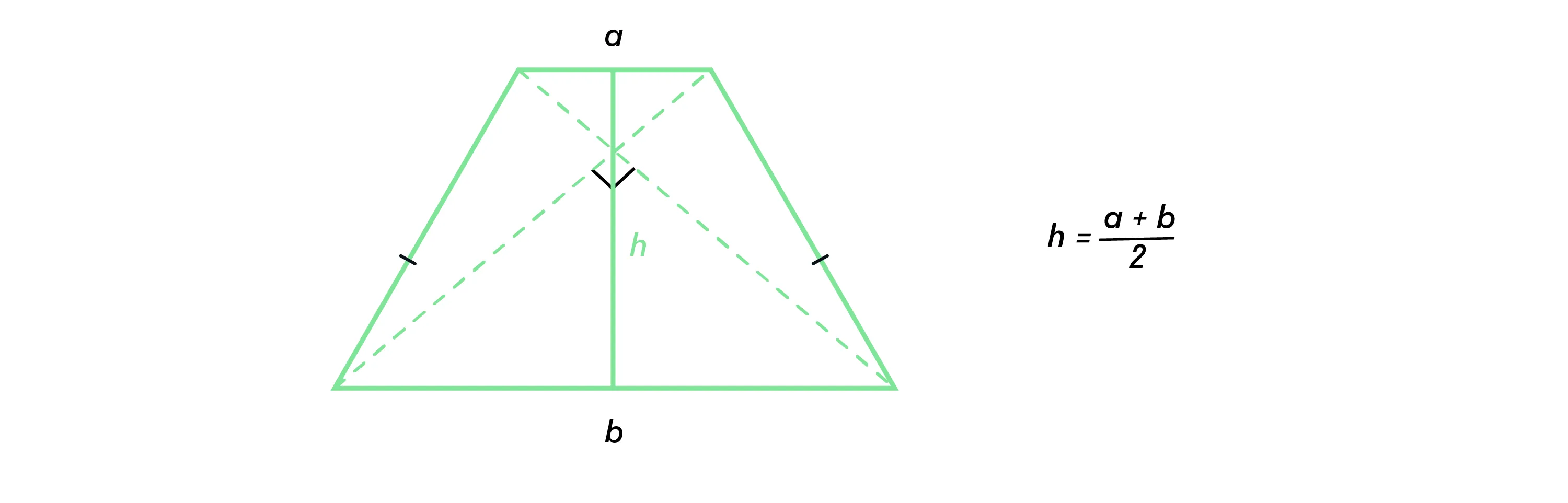
2. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

   

Проверить, насколько хорошо вы усвоили тему «Трапеция», можно в нашем бесплатном тренажёре ЕГЭ. Переходите по ссылке и делитесь с друзьями классным инструментом, с помощью которого можно закрыть пробелы в знаниях и подготовиться к контрольным и экзаменам!