Проверьте знания по математике бесплатно

Узнать бесплатно

Открыть диалоговое окно с формой по клику

Формула длины вектора

184.1K

Сегодня мы поговорим с вами о таких понятиях, как вектор и его длина. Эти термины достаточно популярны в алгебре, геометрии и физике. С их помощью можно решать как очень легкие задачи, так и комплексные с разными физическими величинами и математическими правилами. Сложная ли эта тема? Нет, совсем несложная, но очень и очень важная, поэтому мы посвятим сегодняшнюю статью ей. Приятного чтения!

Что такое векторы и какими они бывают

Как обычно, мы начнем с самого важного: с определения.

Вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.

Вектор обозначают знаком →, например . Как вы заметили, вектор можно выразить одной латинской буквой, а можно — сочетанием двух букв, которыми мы назовем точками начала и конца вектора.

Векторы

Нулевой вектор — вектор, начало которого совпадает с его концом. Обозначается он так:

Как вы уже знаете, векторы бывают коллинеарными и неколлинеарными, сонаправленными и противоположно направленными. Теперь давайте подумаем, что объединяет все виды векторов без исключения. Правильно, у всех есть длина! О том, что это такое, мы и поговорим дальше.

Длина вектора

Длиной или модулем вектора называется длина направленного отрезка, определяющего вектор.

Иногда в математике длину вектора называют модулем. Это легко запомнить, так как длина вектора обозначается с помощью знака | |. Например: . Альтернативное название длины вектора дает нам отличную подсказку: она не может быть отрицательной, в какую бы сторону вектор ни был направлен. А вот нулевой — пожалуйста!

Длина нулевого вектора всегда равна нулю.

Здесь вам может стать интересно, зачем нам нужно знать, как найти длину вектора, и это очень хороший вопрос. Причин может быть множество, но мы выделим несколько главных:

Чтобы определить равенство векторов, необходимо знать их длины. Векторы являются равными, если равны их длины, и сами векторы — сонаправленные.
Вычислив модуль вектора, мы можем рассчитать другие величины.
Например, в физике сила — это векторная величина, т. е. имеет направление. Если вычислить модуль силы, мы можем рассчитать массу тела, его ускорение и т. д.
В геометрии с помощью длины векторов мы можем определить угол между ними, их скалярное произведение.

Достаточно весомые аргументы для нахождения этой величины, правда? Самое время перейти от слов к делу: давайте научимся вычислять длину вектора через свои координаты!

Как можно найти длину вектора по его координатам

Используя прямоугольную систему координат, нарисуем вектор АВ (х, у) из точки (0; 0). Тогда его можно будет считать радиус-вектором для векторов АВ₁ и АА₁.

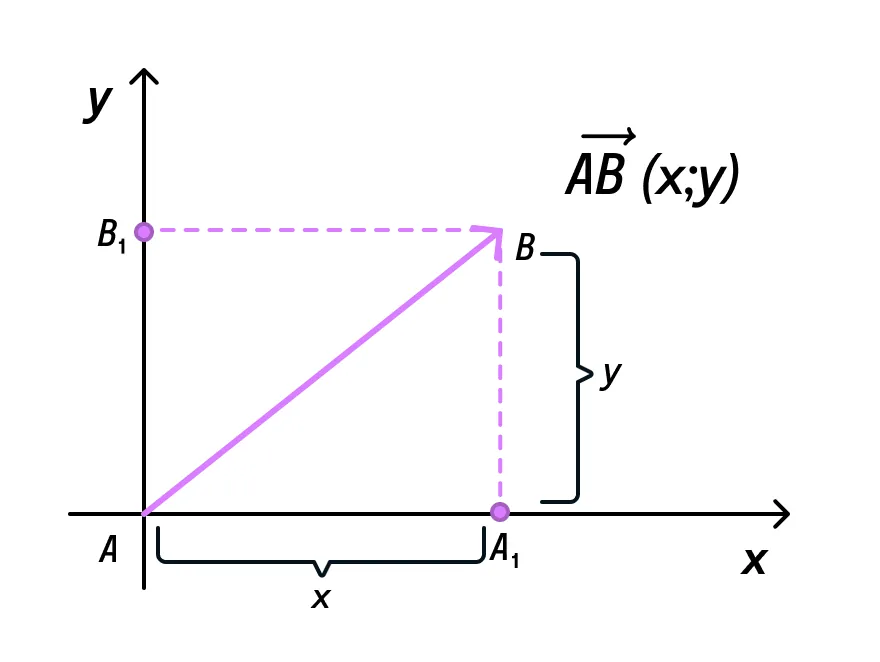
Вектор AB в прямоугольной системе координат

Давайте обозначим длину вектора |АВ₁| = у, длину вектора |АА₁| = х. Треугольники АА₁В и АВ₁В являются прямоугольными, где АВ — гипотенуза. Теперь вспомните, как можно найти длину гипотенузы, зная длины катетов. Верно, через теорему Пифагора! Составим выражение для АВ:

Это значит, чтобы найти длину вектора нужно взять квадратный корень из суммы квадратов его координат. В общем виде эту формулу для длины вектора записывают так — длина вектора :

Если мы будем рассматривать векторы в трехмерном пространстве, формулу нахождения длины вектора можно рассчитать так:

Давайте разберемся, как работают эти формулы для нахождения длины вектора, на примерах. Вы можете решать задания самостоятельно, а потом свериться с нами: так будет еще эффективнее!

Пример № 1

Найдите модуль вектора .

Решение:

Ответ:

Пример № 2

Проведите вычисление длины вектора по его координатам {-2; 0; 5}.

Решение:

Ответ:

Пример № 3

Определите координату х вектора , если его координата по у равна 6, а длина вектора 10.

Решение:

Ответ: .

Уверены, что у вас все блестяще получилось!

Как найти длину вектора по двум точкам

Давайте подумаем, как решать задачи, если нам не даны координаты вектора. Для этого нужно понять, как найти длину вектора по двум точкам — координатам начала и конца. Вспомним: координаты вектора с точкой А (х_а; у_а) и В (х_в; у_в) можно рассчитать так: (х_в – х_а; у_в – у_а). А значит, длину вектора мы определим, если подставим эти выражения в формулу для ее нахождения:

Пример № 4

Найти длину вектора , если В (4; 6), С (-2; 0).

Решение:

Ответ:

Как найти длину вектора по теореме косинусов

Пришло время разобраться, как длина вектора связана с теоремой косинусов. К сожалению, не во всех задачах дано нужное количество информации, чтобы определить длину вектора — тут-то нам и поможет теорема. Вспомним ее!

Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Итак, чтобы определить длину стороны треугольника, нужно сложить квадраты двух других сторон, вычесть удвоенное произведение длин сторон на косинус угла между ними и взять корень из полученного числа. Так мы получим формулу нахождения длины вектора через теорему косинусов.

Формулы нахождения длины вектора через теорему косинусов

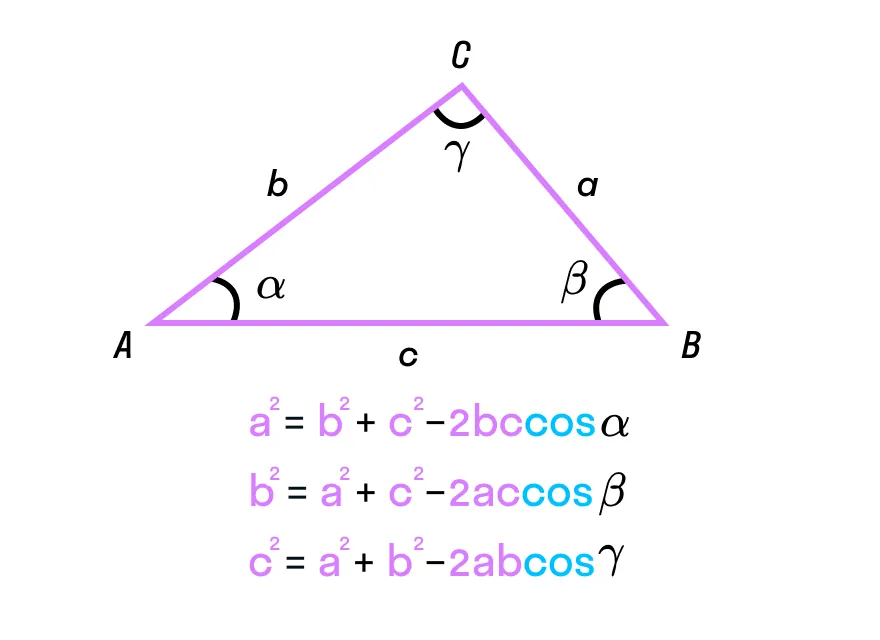
Предположим, что нам необходимо узнать длину вектора или . Тогда, чтобы воспользоваться теоремой косинусов, нам нужно найти длину векторов и и угол между ними.

Пример № 5

Длины векторов и равны 5 и 12 соответственно, а угол между ними равен π/3. Проведите вычисление длины вектора .

Решение:

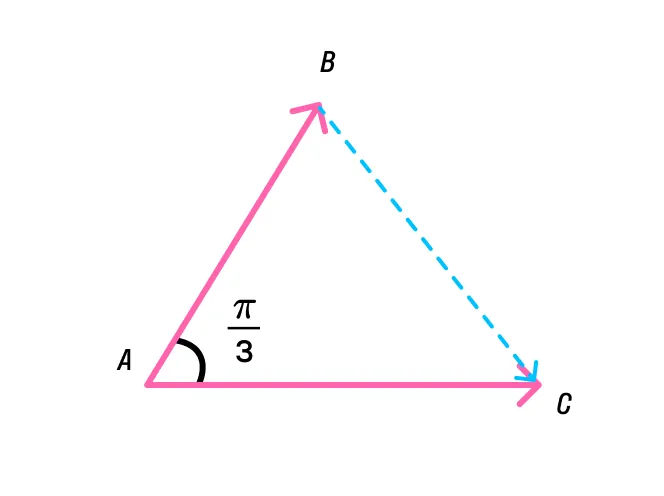
Векторы AB, AC и BC

Ответ:

Сегодня мы обсудили с вами все основные моменты, которые касаются длины вектора: изучили теорию и дополнили ее базовыми задачами. Дело осталось за малым — выучить весь материал и практиковаться! В этом вам помогут курсы по профильной математике в школе Skysmart. Уникальная платформа, учителя-профессионалы, индивидуальная программа — уроки просто созданы для того, чтобы стать уверенными в математике. Ждем вас на занятиях и до новых встреч!