Перпендикулярные прямые - это две прямые, лежащие в одной плоскости, которые пересекаются под прямым углом (90 градусов) и образуют четыре прямых угла. Пример: оси координат на плоскости (xOy) являются перпендикулярными.
Скорее всего, вы смогли бы отыскать три варианта:
Прямые параллельны друг другу;
Прямые совпадают, накладываются друг на друга;
Прямые пересекаются.
И были бы абсолютно правы! Интересно, что в пункте № 3 скрывается один интересный случай, который мы рассмотрим подробнее сегодня, а именно: прямые могут быть перпендикулярны друг другу.
Что это означает? Рассмотрим определение перпендикулярных прямых.
Для кого эта статья:
- Школьники и студенты, изучающие геометрию
- Педагоги и учителя, ищущие материалы для преподавания
- Люди, интересующиеся математикой и её практическим применением
Основные определения
Перпендикулярные прямые — это прямые, которые пересекаются друг с другом под углом 90 градусов. Обозначение перпендикулярных прямых: а ┴ b.
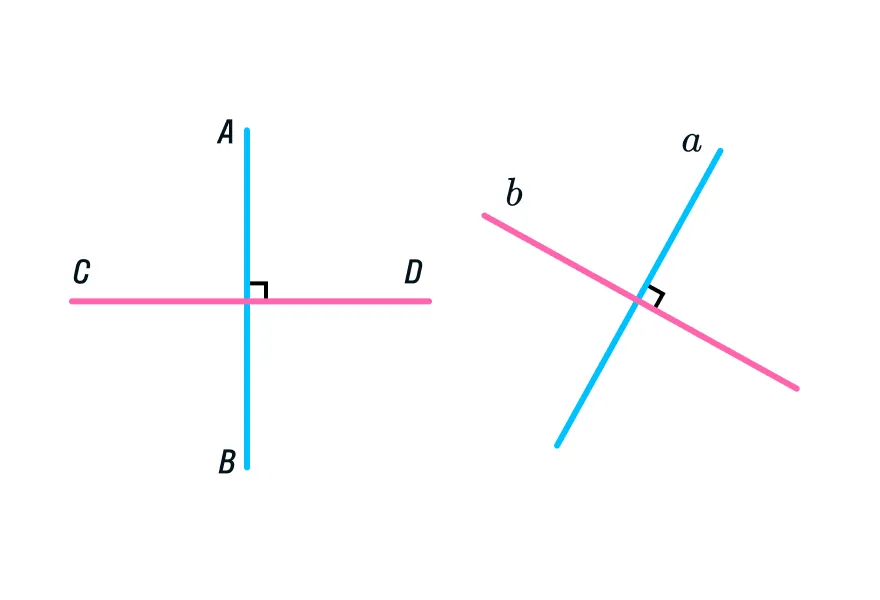
Угол, равный 90 градусам, в математике называют прямым и помечают на чертеже квадратиком.
Еще один интересный факт из мира геометрии: если при пересечении двух прямых один из образовавшихся углов равен 90°, то и все остальные углы — прямые, а их сумма будет равна 360°.
Перпендикулярные отрезки — это отрезки, лежащие на перпендикулярных прямых.
Чтобы называться перпендикулярными, отрезкам не обязательно пересекаться самим. Достаточно, чтобы угол между прямыми, на которых они лежат, был равен 90°.
В качестве задачки со звездочкой давайте вспомним, в каких фигурах могут встречаться перпендикулярные отрезки (стороны)? Наверняка вы сразу назовете квадрат и прямоугольник, но также подходит прямоугольный треугольник и даже прямоугольная трапеция — с ней вы познакомитесь на уроках геометрии в 8-м классе.
Также перпендикулярно к стороне могут располагаться различные элементы внутри фигуры. Попробуйте расположить перпендикулярно друг другу диаметр и радиус окружности, две хорды, биссектрису угла треугольника (кстати, последнее задание получится выполнить только в случае, если проводить биссектрису угла к основанию равнобедренного треугольника).
Как мы видим, прямые очень часто пересекаются под углом 90 градусов. Можно сказать, это своего рода обычное, будничное поведение прямых. Прямые углы окружают нас повсюду: в комнате, на оживленных улицах города, в бассейне и даже в любимой книге.
Способы построения перпендикулярных прямых
Но как можно построить перпендикулярные прямые? Что для этого может понадобиться? Давайте разберем все доступные нам способы.
Самый легкий — воспользоваться транспортиром. Построим прямую а и точку А, не лежащую на этой прямой. Совместим значение 90 градусов с точкой таким образом, чтобы нижняя часть транспортира в виде линейки полностью совпала с прямой, и сделаем засечку в отверстии транспортира. Соединим точку А с поставленной засечкой до пересечения с прямой.
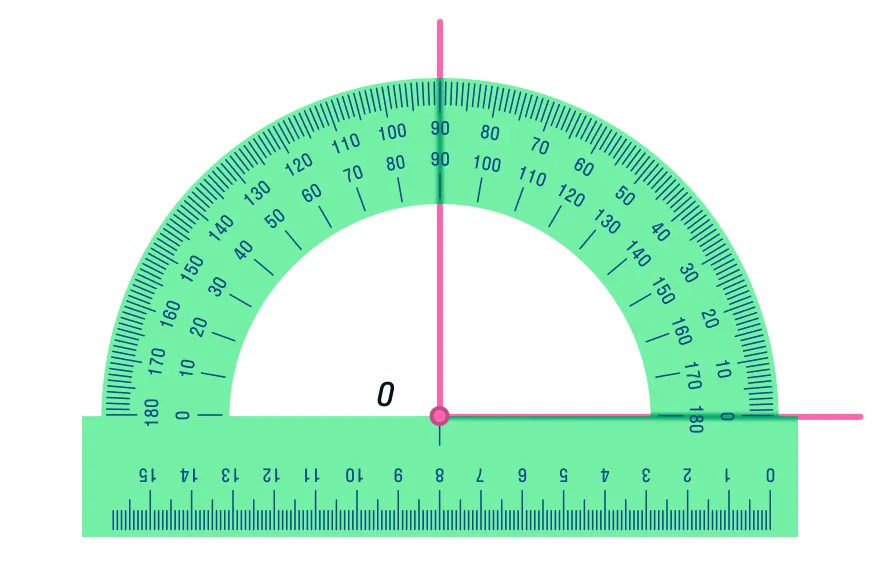

Но что делать, если транспортир благополучно забыт дома и у нас есть только линейка и угольник? Внимательно рассмотрите рисунок и попрактикуйтесь в построении дома.
Получи больше пользы от Skysmart:
-
Прокачивай знания на курсах математики
-
Выбирай из 1200+ репетиторов по математике
Записывайся на бесплатные курсы для детей
Теорема о перпендикулярных прямых и ее доказательство
«Кто это вообще придумал?», — можете возразить вы. «Почему мы должны этому верить? Вдруг все иначе, а нас обманывают». Если это так, то ваши опасения — показатель пытливости ума!
Что такое теорема? Это утверждение, нуждающееся в доказательстве. Это означает, что его не принимает на веру никто: ни вы, ни учитель, ни самый великий ученый. Есть много способов доказательства теорем, один из которых — метод от противного. Используя его, мы будто соглашаемся с противоположным заявлением и рассуждаем, что из этого последует.
Например, попробуем доказать утверждение «осенью грачи улетают на юг» методом от противного. Предположим, что грачи остаются зимовать в наших городах. Тогда мы должны видеть их осенью и зимой повсеместно, а в небе не должно быть видно признаков масштабного перелета. Так ли это на самом деле? Конечно же, нет.
Теперь с помощью этого метода попробуем доказать теорему о перпендикулярных прямых.
Предположим, что теорема ложна, а значит, через точку, лежащую на прямой, можно провести несколько перпендикулярных прямых.
Проверим гипотезу:
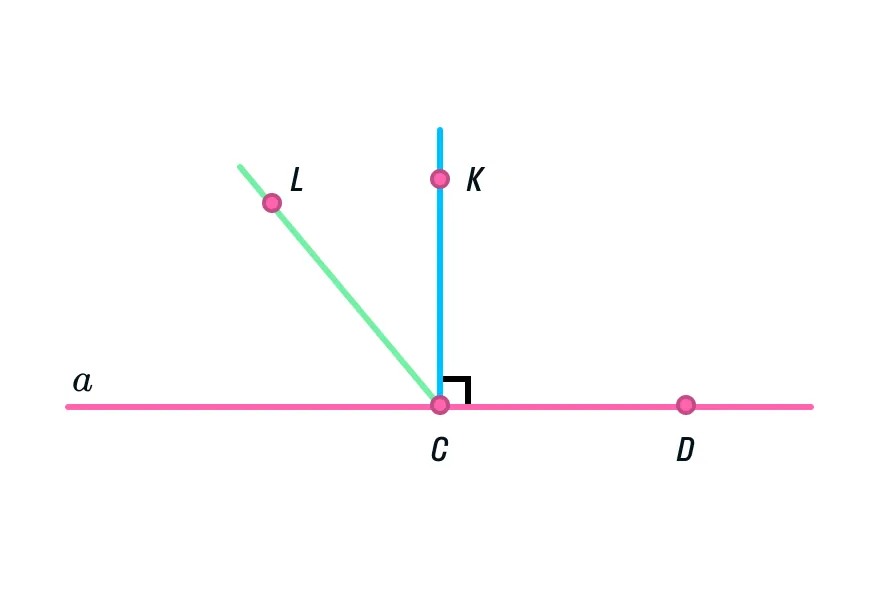
Возьмем линейку и проведем прямую а, отметив на ней точки С и D.
Далее построим перпендикулярную прямую из точки С. Угол КСD равен 90°.
Отрезок КС находится на прямой, перпендикулярной а.
Предположим, что есть еще одна прямая, перпендикулярная а. Проведем ее через точку С и отметим на ней точку L.
Тогда угол LCD равен 90° и угол КСD равен 90°.
Пункт номер 5 невозможен: от отрезка CD можно отложить только один прямой угол в данной плоскости.
А значит, через точку С можно провести только одну прямую, перпендикулярную прямой а.
Что и требовалось доказать: вы — молодцы!
Свойства перпендикулярных прямых
Перпендикулярные прямые обладают свойствами, которые можно использовать при решении геометрических задач. Давайте изучим их и приведем доказательство каждого.
Две прямые, перпендикулярные к третьей, не пересекаются
Конечно же, это свойство хорошо просматривается при построении. Но как мы уже выяснили, математики — народ сомневающийся, поэтому попробуем обосновать, почему это так.
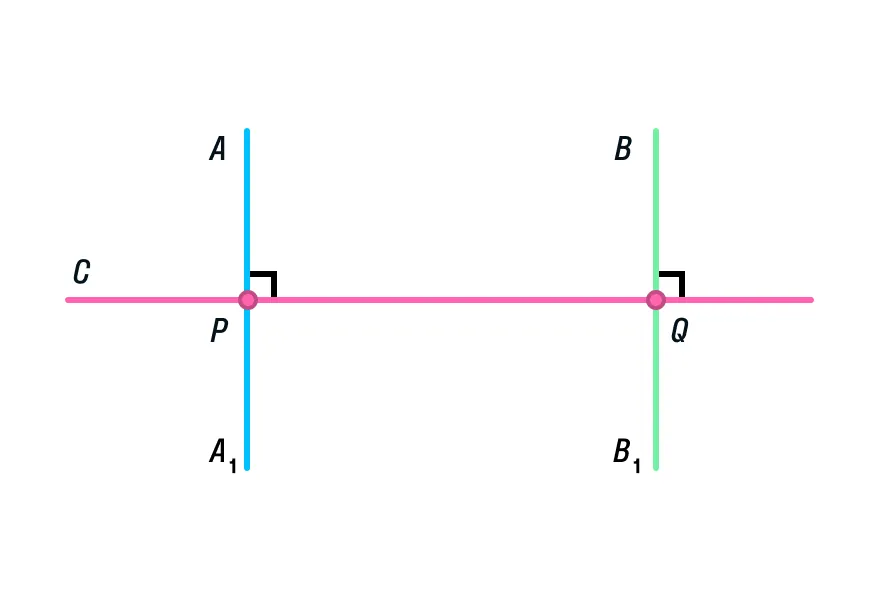
Предположим, что прямые АА1 и ВВ1 все же пересекутся в точке К. Что бы это значило? Что мы совершили невероятное и опровергли теорему о перпендикулярных прямых! Ведь тогда получается, что через точку К проходит несколько перпендикулярных прямых, которые в свою очередь пересекают прямую а под углом 90 градусов! Как было сказано выше, это невозможно, а значит и прямые АА1 и ВВ1 не пересекаются.
Перпендикуляр, проведенный из точки к прямой, называется расстоянием от прямой до этой точки
Интересно, что такое расстояние является кратчайшим.
Представьте, что вам необходимо проложить путь от вас до огромного торгового центра, состоящего из множества магазинчиков. Вам не важно, в какой из них заглянуть, вы просто хотите потратить на дорогу как можно меньше времени. Какой путь вы выберете?
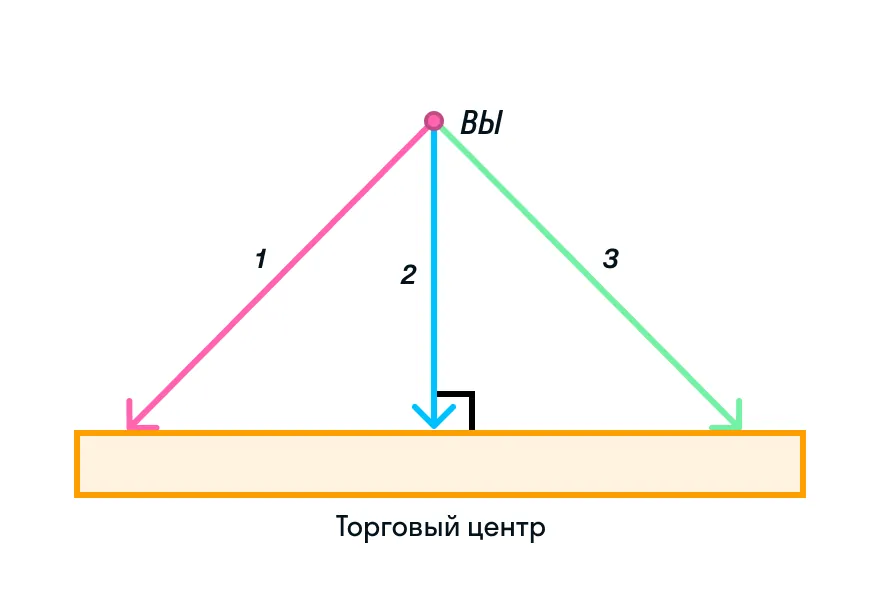
Конечно же, путь номер 2! Но есть ли этому научное объяснение?
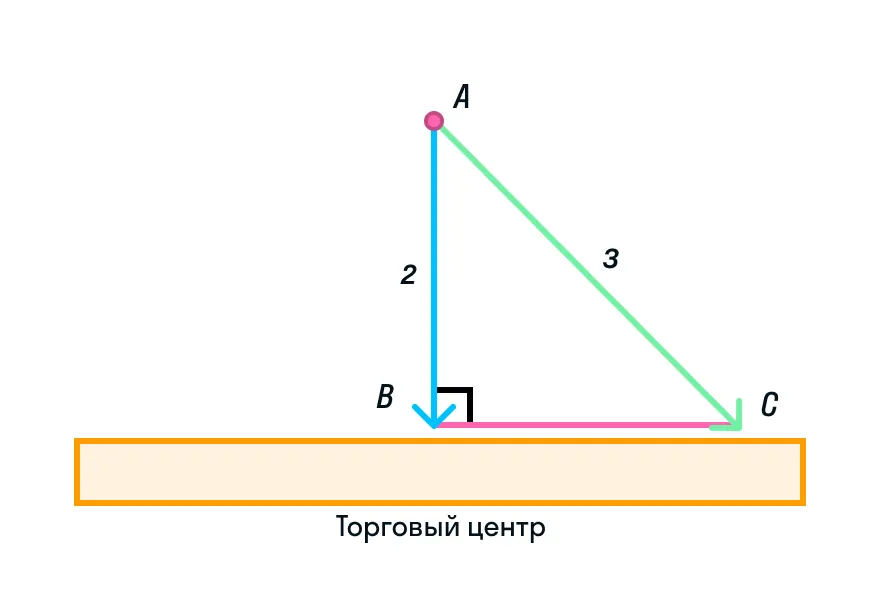
Треугольник АВС прямоугольный, АВ и ВС— катеты, АС — гипотенуза. Согласно соответствию углов и сторон, в треугольнике наибольшая сторона лежит напротив наибольшего угла. Таким углом является прямой угол В, а наибольшая сторона — гипотенуза АС. Под каким бы углом мы ни расположили гипотенузу, она всегда будет больше остальных сторон.
В задачах по геометрии часто просят найти расстояние между различными элементами: между двумя точками, между точкой и прямой, между двумя прямыми. Теперь вы знаете, что под расстоянием подразумевают перпендикуляр! Благодаря этому знанию вы избежите множества ошибок, ведь между двумя элементами можно провести бесконечное множество прямых (и кривых), но только один вариант будет верным.
Кстати, перпендикуляр, проведенный из вершины угла фигуры на прямую, содержащую противоположную сторону, известен под именем высота. С высотами связано множество теорем и свойств, которые вы будете изучать немного позже. В качестве интриги оставим вам пример того, где находится точка пересечения высот в треугольниках разного типа. Заметили что-то необычное?
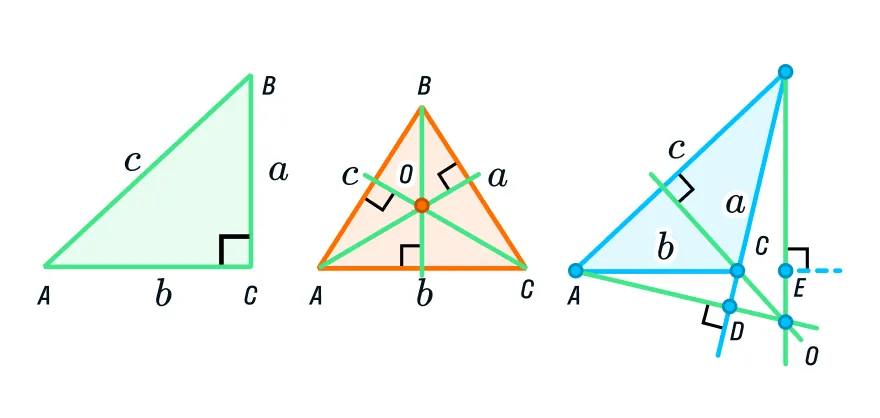
Применение знания о перпендикулярных прямых
Напоследок ответим на вопрос, который мог возникнуть у некоторых из вас: «А как в древности люди решали вопрос с построением перпендикулярных прямых, прямых углов в частности? Были ли у них приспособления для этого?»
Построение прямых углов было важным умением даже в древности, так как от этого зависела крепость и устойчивость возведенных стен зданий, мостов, механизмов для строительства. Один лишний градус — и целый город мог оказаться в опасности из-за обрушившегося дворца или башни.
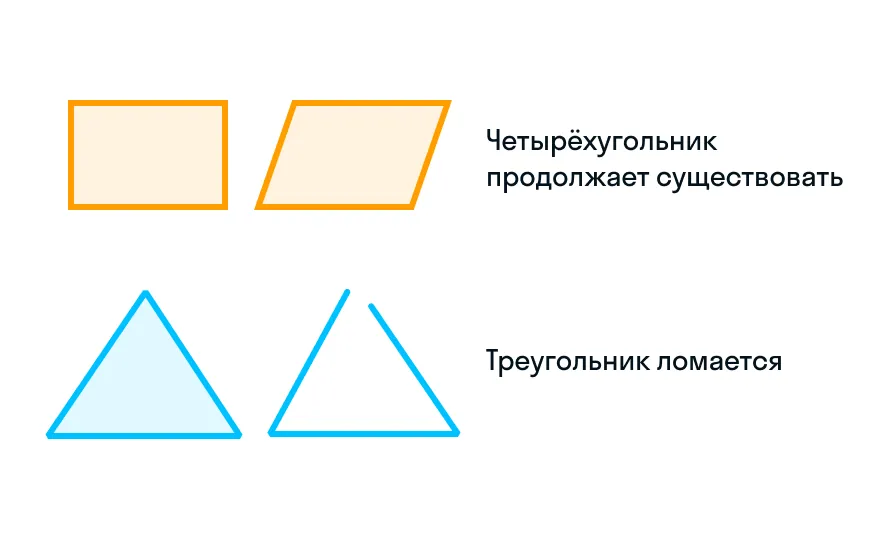
Древние зодчие поняли, что возлагать все надежды на четырехугольники не стоит, потому что квадраты и прямоугольники легко превращаются в параллелограммы, меняя величину углов и оставляя неизменными длины сторон. Стоит только немного потянуть за «ушки» квадрата, как он начинает беспощадно ломать прямые углы, а ведь в условиях строительства многое может пойти не так и искривить конструкцию: ветер, изменение температуры, неточность мастера.
Хорошо, что есть более стабильная фигура — треугольник. Все дело в соотношении его сторон и углов, а еще в невозможности создать несколько треугольников из сторон заданной длины. Если у вас есть отрезки длиной 6, 8 и 10 сантиметров, из них можно составить только один треугольник. В случае, если одна сторона растянется под действием нагрузки или сожмется из-за понижения температуры — треугольник просто перестанет существовать.
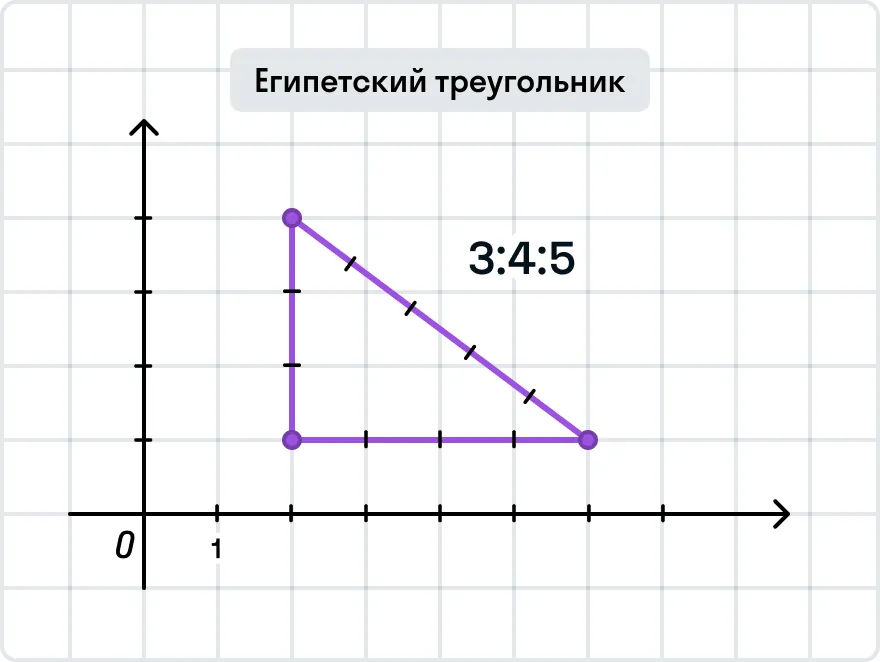
С этой точки зрения прямоугольные треугольники — лучшие друзья архитекторов, которые хотят строить ровные и красивые здания. Зодчие Древнего Египта использовали шнур или веревку, на которых через равные расстояния были завязаны 12 узлов. Строители натягивали такой шнур, создавая прямоугольный треугольник со сторонами 3, 4 и 5 единиц. Такой метод получения угла, равного 90 градусам, был сверхточным, а по сторонам-катетам-шнурам можно было выкладывать кирпичи или камни.
Удивлены? Еще больше поразительных фактов и, самое главное, помощь в понимании алгебры и геометрии вы получите на курсах профильной математики в онлайн-школе Skysmart. Секреты древних архитекторов, бытовые задачки и подготовка к экзаменам — все на удобной платформе с опытными учителями. Ждем вас!