Вы наверняка помните значения тригонометрических функций основных аргументов:
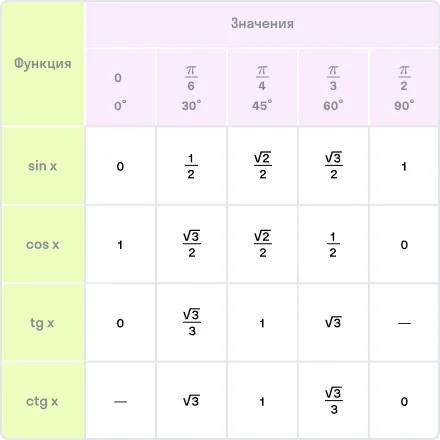
Но что делать, если в задаче просят вычислить
Всего формул приведения тридцать две штуки, но прежде чем мы перейдем к формулам, давайте договоримся, что точку тригонометрической окружности, отвечающую углу
Для кого эта статья:
- Студенты и школьники, изучающие математику и тригонометрии
- Учителя и репетиторы по математике, которые ищут материалы для объяснения темы
- Все желающие улучшить свои знания и навыки в тригонометрии
Список формул приведения
Формулы приведения c опорной точкой
-
-
-
-
-
-
-
-
Формулы приведения c опорной точкой
-
-
-
-
-
-
-
-
Формулы приведения c опорной точкой
-
-
-
-
-
-
-
-
Формулы приведения c опорной точкой
-
-
-
-
-
-
-
-

Доказательство формул
Чтобы убедиться, что формулы рабочие, рассмотрим примеры доказательств нескольких из них.
Для этого нам нужно будет вспомнить формулы сложения для синуса и косинуса:
-
-
Формула приведения с синусом
Разберем первый пример формулы приведения с синусом:
По формуле синуса суммы представим левую часть выражения:
Вычислим
Таким образом,
Формула приведения с косинусом
Рассмотрим также пример формулы приведения с косинусом и докажем ее:
Аналогично распишем левую часть по формуле косинуса суммы:
Вычислим
Следовательно,
Формула приведения с тангенсом
Чтобы доказать формулу приведения с тангенсом, нужно вспомнить, что тангенс — это отношение синуса к косинусу. Тогда для доказательства нужно лишь дважды использовать формулы сложения — попробуйте сами на формуле
При желании таким образом вы сможете доказать справедливость всех формул.
Получи больше пользы от Skysmart:
-
Подготовься к ОГЭ на пятёрку
-
Подготовься к ЕГЭ на высокие баллы
Записывайся на бесплатные курсы для детей
Решай задания в бесплатном тренажёре ЕГЭ
Таблица формул приведения
Нередко можно встретить такой вариант оформления формул приведения — в виде таблицы.
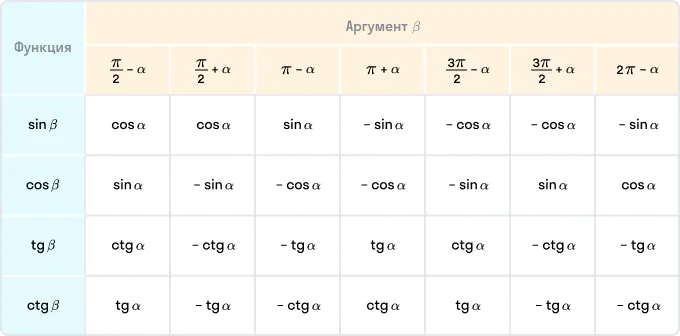
Для того чтобы воспользоваться этой таблицей, выберите строку с нужной функцией и столбец с необходимым аргументом — на их пересечении вы узнаете ответ.
Например, нужно упростить
Маленькую распечатанную таблицу формул приведения тригонометрических функций удобно иметь в пенале на случай неожиданных контрольных.
Как запомнить формулы приведения
Одно дело — воспользоваться формулами, а совсем другое — выучить их. Знать наизусть все формулы приведения или всю таблицу — дело нелегкое и, к счастью, абсолютно ненужное.
Поэтому познакомимся с мнемоническим алгоритмом:
-
Представьте аргумент в виде
-
Изобразите (на листе или мысленно) на единичной окружности данный угол.
-
С помощью окружности определите знак исходной функции. Полученная функция в правой части будет иметь такой же знак.
Напоминаю знаки тригонометрических функций во всех четвертях тригонометрической окружности:
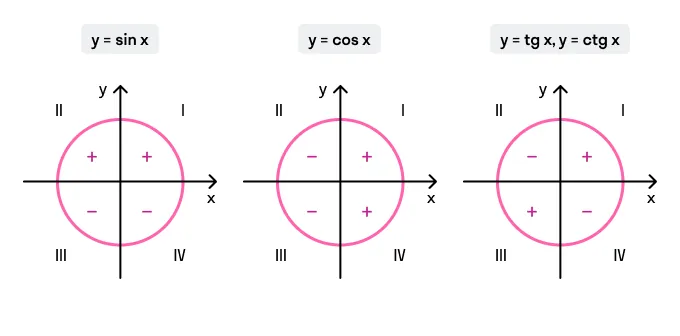
-
Если в аргументе у опорной точки
Если в аргументе у опорной точки
Вот с этим пунктом изменения или сохранения функции возникает постоянная путаница. А запомнить поможет «правило лошадки».
Таким образом, формулы приведения — это тригонометрические тождества вида
Задание 1
Найдите значение выражения
Вы видите, что каждое слагаемое выражения — это формула приведения тригонометрической функции. Упростим их по отдельности.
-
Сначала нужно представить аргумент в виде
-
Далее изображаем данный угол на тригонометрической окружности:
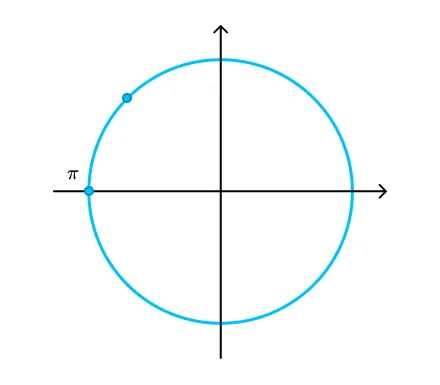
-
Определяем знак исходной функции, то есть синуса. Синус этого угла принимает положительные значения.
-
В конце определяем, меняется ли функция. В этом нам поможет «правило лошадки»: опорная точка
Значит,
Приведем аналогичные рассуждения для всех слагаемых в выражении.
-
Аргумент уже представлен в виде
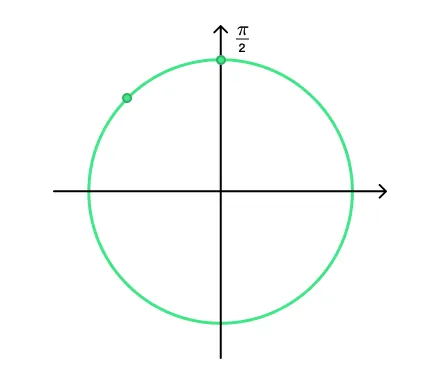
-
Косинус во второй четверти тригонометрической окружности принимает отрицательные значения.
-
Опорная точка
Значит,
-
Аргумент уже представлен в виде
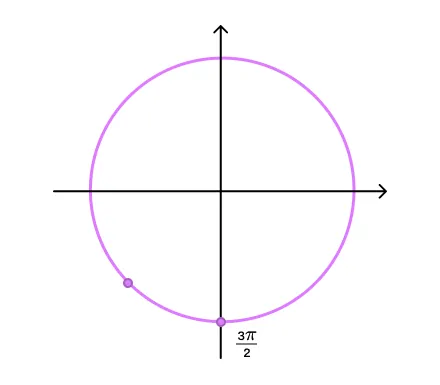
-
Косинус в третьей четверти тригонометрической окружности принимает отрицательные значения.
-
Опорная точка
Значит,
А теперь запишем преобразованные выражения в наше исходное и упростим:
Обратите внимание, к какому простому виду удалось привести это сложное, на первый взгляд, выражение.
Задание 2
До этого момента мы говорили о формулах приведения тригонометрических функций углов, выраженных в радианах. Однако мы понимаем, что градусы и радианы — это разные способы представления одних и тех же углов или аргументов, поэтому тригонометрические формулы приведения работают и для выражений с градусами.
Разберем на примере: найдите значение выражения
В этом случае важно заметить, что
Так как первый шаг выполнен, то продолжаем идти по алгоритму.
Косинус в первой четверти тригонометрической окружности принимает положительные значения.
Опорная точка
Значит,
Запишем преобразованные выражения в наше исходное и упростим:
Формулы приведения в тригонометрии занимают второе место по важности и частоте использования после основного тригонометрического тождества, так что осваивайте теоретические материалы, практикуйтесь на задачках, а за другими полезными формулами и самыми хитрыми заданиями приходите на онлайн-курсы математики для детей в Skysmart.

















