Касательная к окружности, секущая и хорда — в чем разница
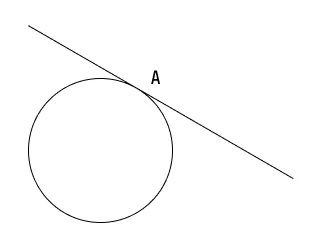
В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.
|
Касательная к окружности — это прямая, имеющая с ней всего одну общую точку. |
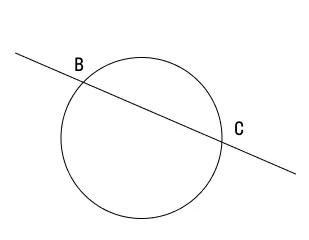
Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).
|
Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой. |
Свойства касательной к окружности
Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.
Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.
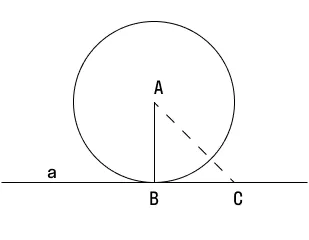
- окружность с центральной точкой А;
- прямая а — касательная к ней;
- радиус АВ, проведенный к касательной.
Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.
Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.
Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.
Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:
Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.
Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.
В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.
Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Задача
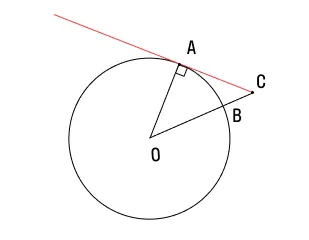
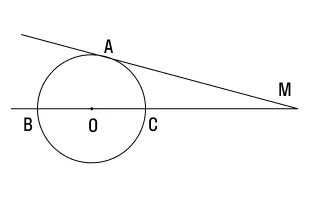
У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.
Решение:
Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.
Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.
∠АОС = 180° - ∠САО - ∠АСО = 180° - 90° - 28° = 62°
Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно,
Ответ:
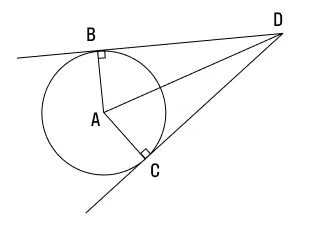
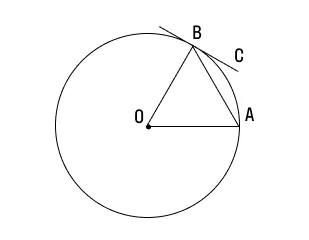
Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.
Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.
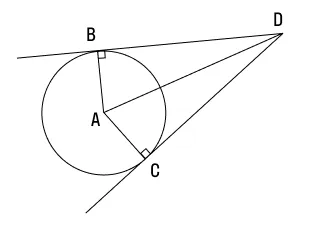
Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.
Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.
Задача 1
У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.
Решение
Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.
∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).
Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:
∠BDC = ∠BDA × 2 = 30° × 2 = 60°
Итак, угол между касательными составляет 60°.
Ответ: ∠BDA = 60°.
Задача 2
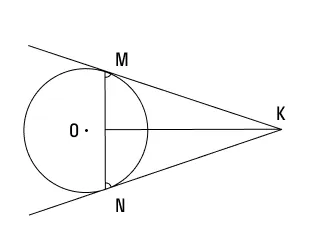
К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.
Решение
Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.
Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.
∠МNК = (180° - ∠МКN) : 2 = (180° - 50°) : 2 = 65°
Ответ: ∠NМК = 65°.
Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.
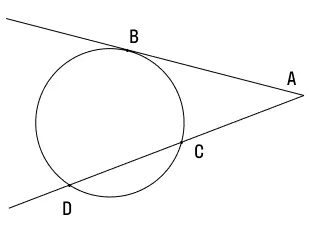
Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.
AB2 = AD × AC
Задача 1
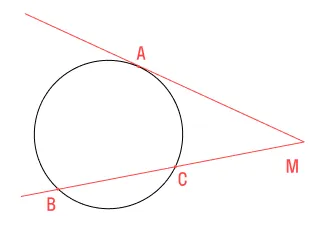
Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.
Решение
Исходя из соотношения касательной и секущей МА 2 = МВ × МС.
Найдем длину внешней части секущей:
МС = МВ - ВС = 16 - 12 = 4 (см)
МА2 = МВ × МС = 16 х 4 = 64
МА = √ 64= 8 (см)
Ответ: MA = 8 см.
Задача 2
Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.
Решение
Допустим, что МО = у, а радиус окружности обозначим как R.
В таком случае МВ = у + R, а МС = у – R.
Поскольку МВ = 2 МА, значит:
МА = МВ : 2 = (у + R) : 2
Согласно теореме о касательной и секущей, МА2 = МВ × МС.
Значит:
(у + R)2 : 4 = (у + R) × (у - R)
Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:
(у + R) : 4 = (у - R)
у = 5R : 3
Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).
Ответ: MO = 10 см.
Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.
∠АВС = ½
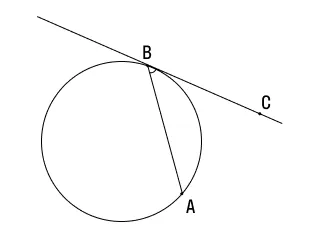
Задача 1
Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.
Решение
Согласно свойствам угла между касательной и хордой, ∠АВС = ½
Ответ:
Задача 2
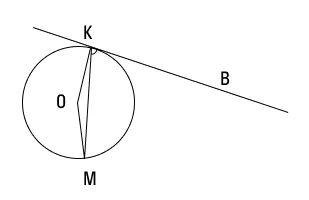
У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.
Решение
Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:
Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.
∠ОКМ = ∠ОМК = (180° - ∠КОМ) : 2
Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:
∠КОМ =
∠ОМК = (180° - ∠КОМ) : 2 = (180° - 168°) : 2 = 6°
Ответ: ∠ОМК = 6°.
