Задачи на квадратной решётке

Задания из ЕГЭ базового уровня

На ЕГЭ по базовой математике встречаются задания двух видов: необходимо дать приближённое значение площади объекта на карте или точное значение площади геометрической фигуры.

Площадь n-угольников

Прежде чем переходить к задачам, советуем повторить формулы по теме «Площадь фигуры».

Задача 1

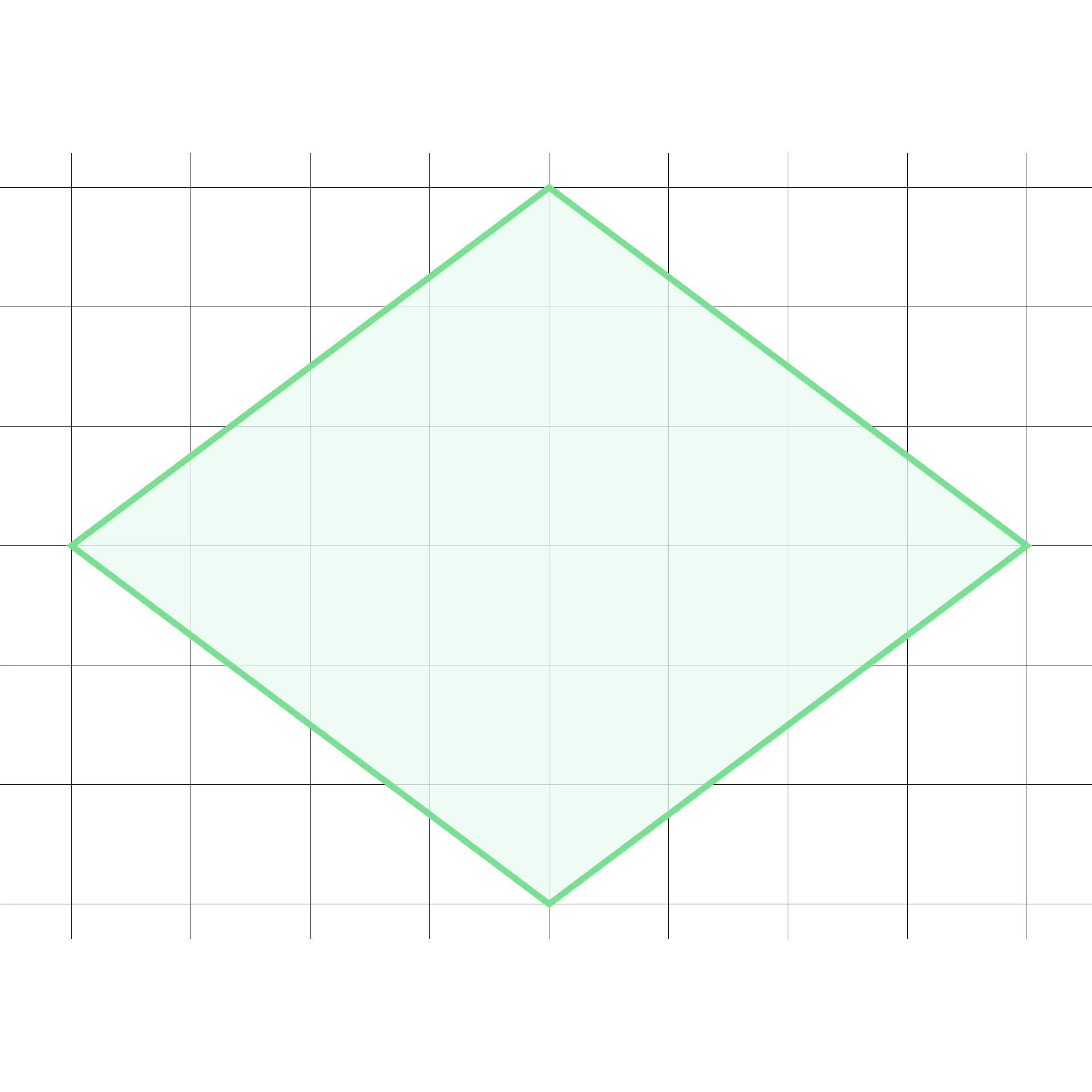
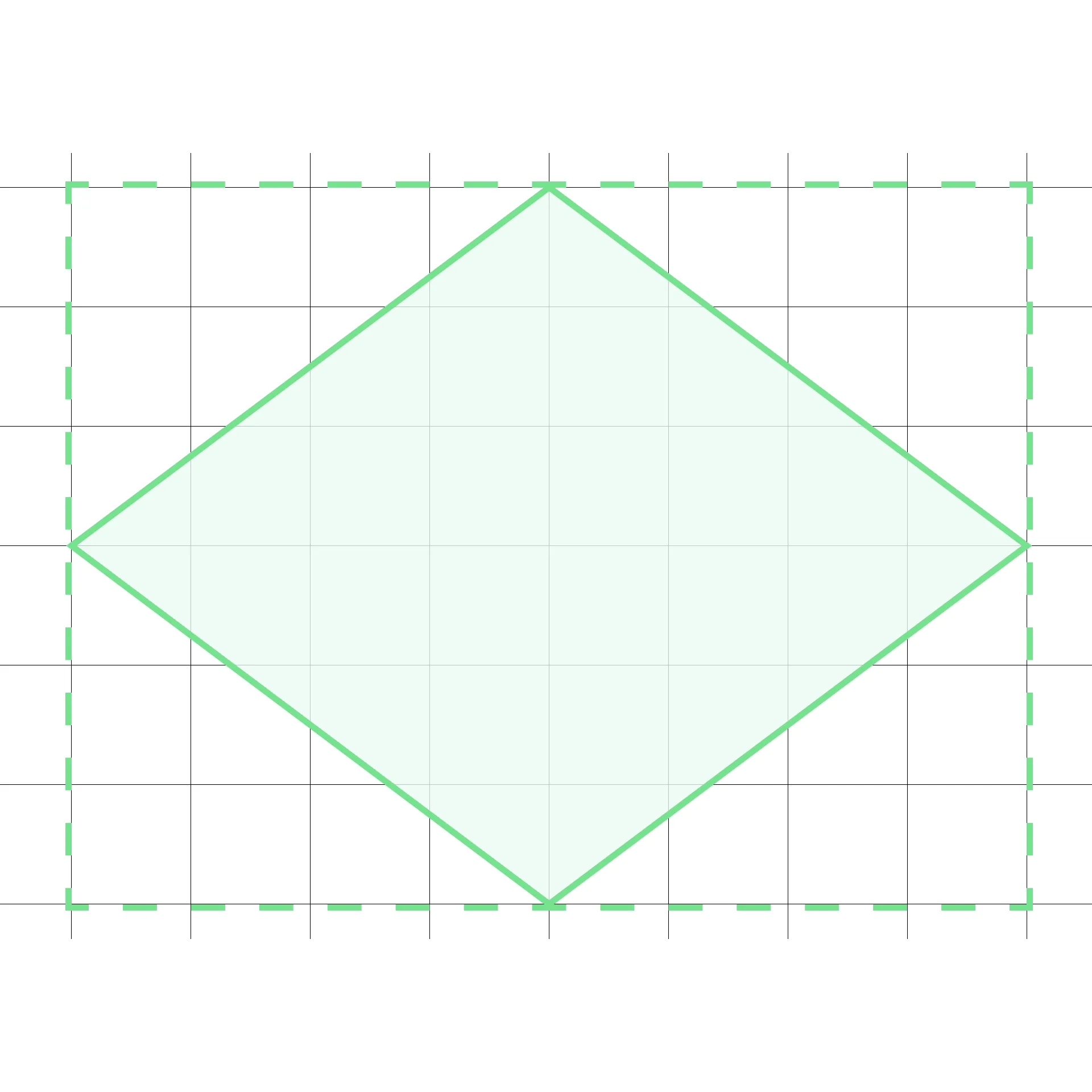
Найдите площадь фигуры, изображённой на рисунке, если сторона клетки равна 10 см.

Решение:

1. Сделаем дополнительные построения и найдём площадь полученного прямоугольника с учётом длины стороны клетки: 60 ⋅ 80 = 4800.

   

2. Заметим, что большой прямоугольник состоит из 4 равных прямоугольных треугольников (незакрашенная область) и ромба (закрашенная область).

   Найдем площадь незакрашенной области:

3. Вычтем из площади большого прямоугольника площадь незакрашенной части: 4800 − 2400 = 2400

Ответ: площадь ромба равна 2400 см².

Задача 2

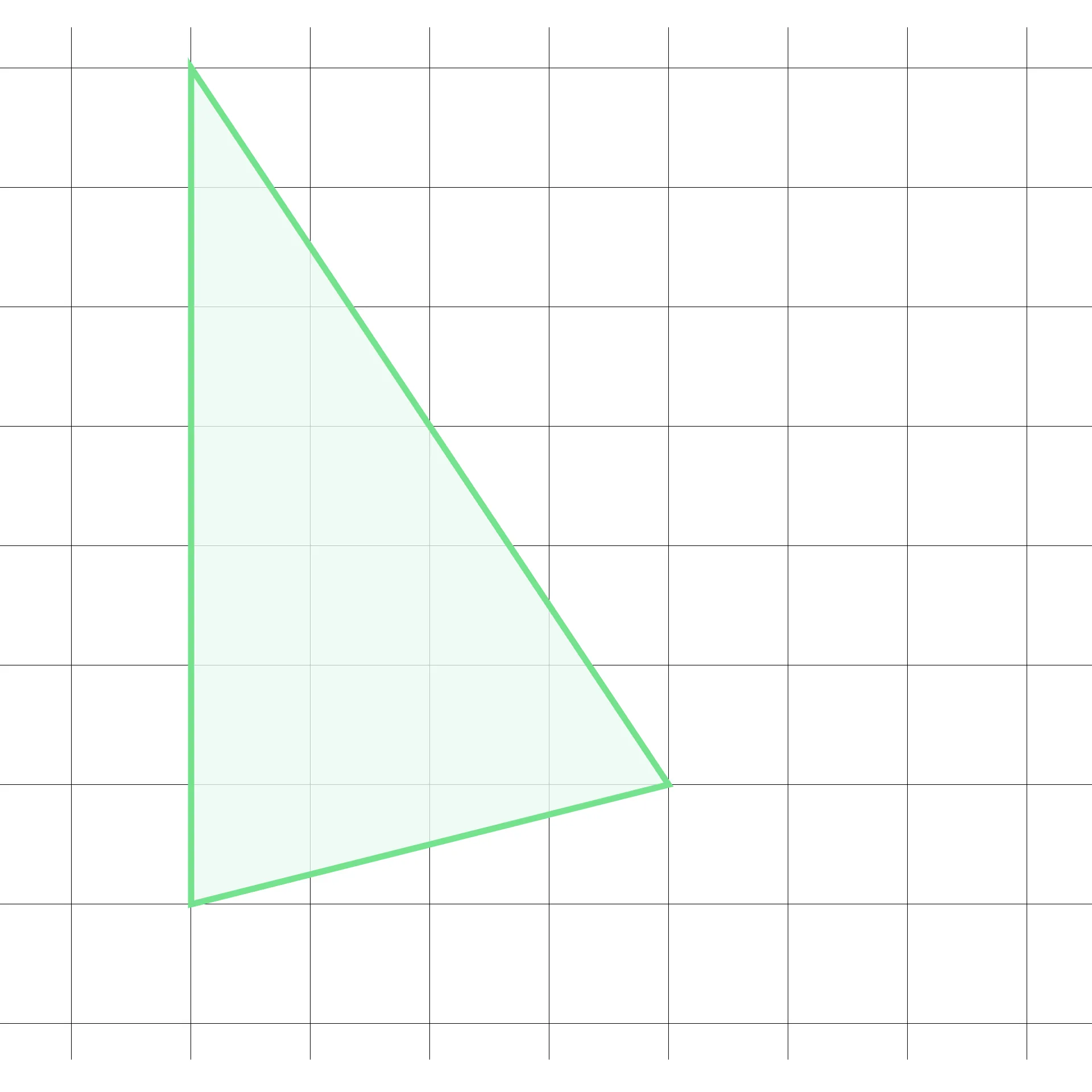
Найдите площадь фигуры, изображённой на рисунке, если размеры каждой клетки равны 1 × 1 см.

Решение:

Мы можем решить эту задачу тем же методом, что и задачу 1 — сделать дополнительные построения и из площади большой фигуры вычесть площадь незакрашенных частей.

А можно сделать иначе:

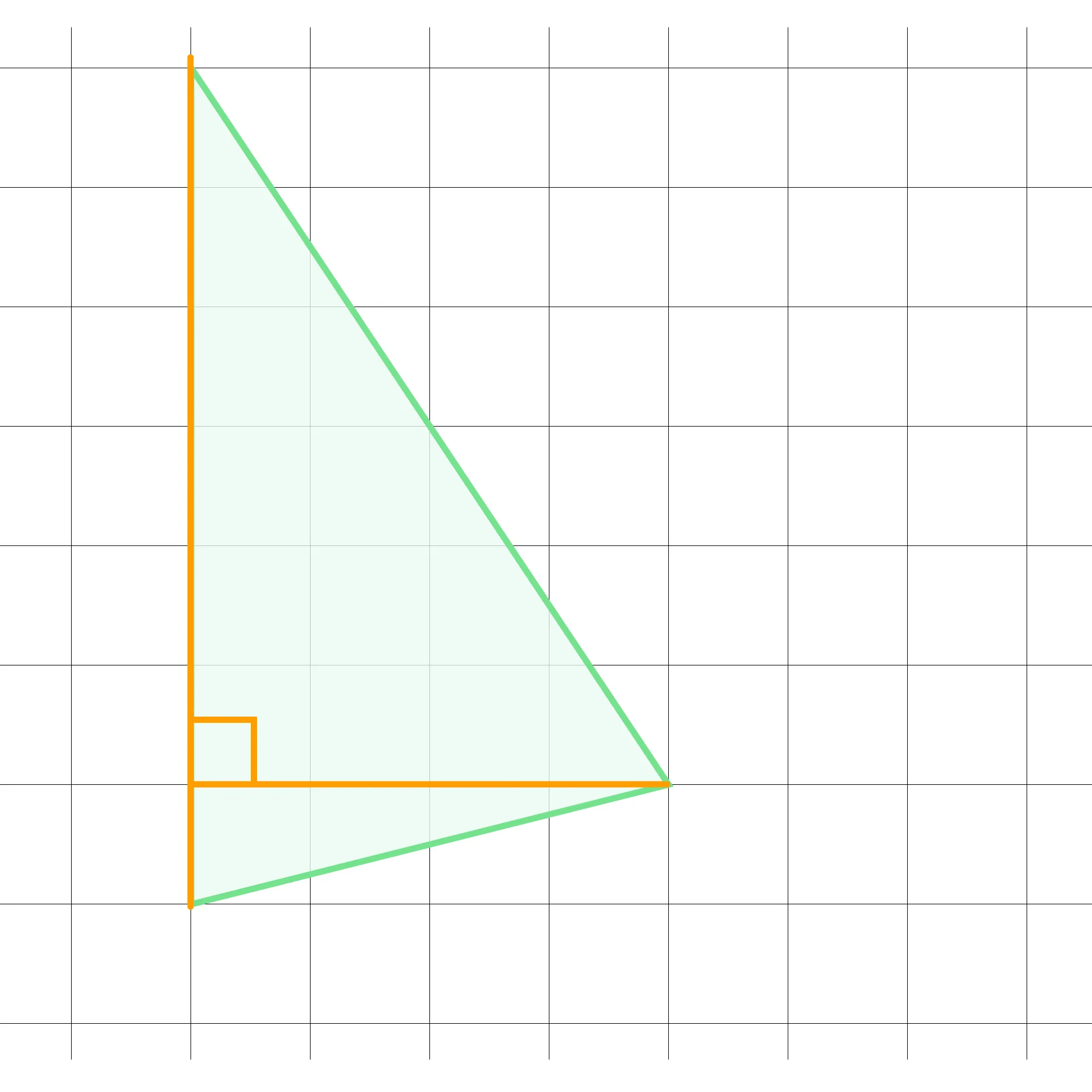
1. Сделаем дополнительные построения: проведём высоту, проходящую ровно по клеточкам, длина которой составляет целое число.

   

2. Высота равна 4, а сторона, к которой провели высоту, — 7.

   Тогда

Задачи на карте

В задачах на карте необходимо найти площадь объекта неправильной формы. Мы будем делить объект на части, анализировать, какую часть от клетки занимает часть объекта, и суммировать приблизительные площади каждой из долей.

Задача 3

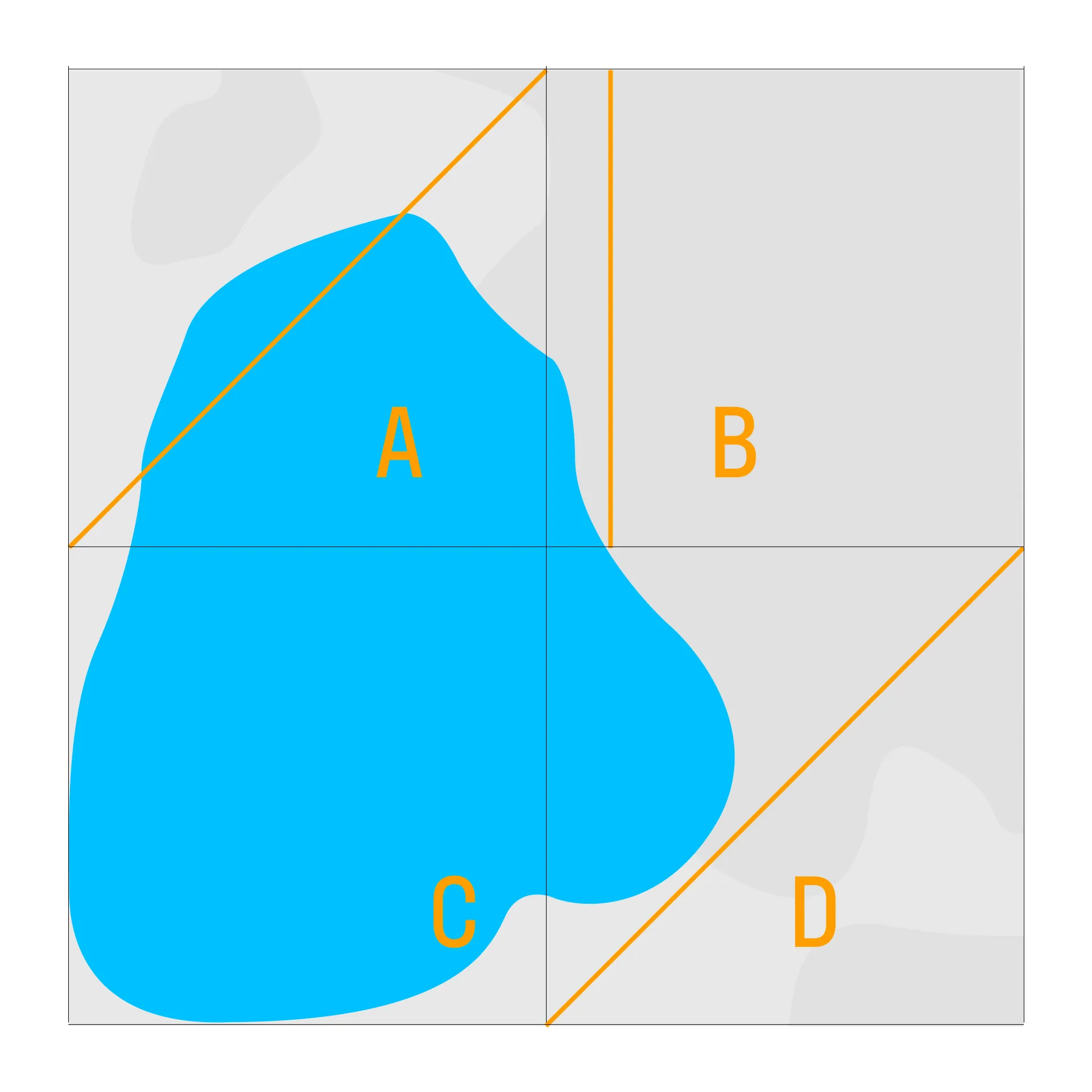
Оцените площадь озера Лебяжье, если размеры клетки 2 × 2 км.

Решение

Обозначим квадраты, которые занимает озеро, буквами, и оценим занимаемую часть.

1. S_клетки = 2 × 2 = 4 км².

2. Клетка А занята больше чем наполовину, т. е. ≥ 2 км².

3. Если сложить занятую площадь клеток В и D, получится чуть меньше половины, т. е. ≤ 2 км².

4. Клетка С почти полностью занята.

5. Итого: озеро занимает чуть больше половины клетки, чуть меньше половины клетки и почти целую клетку. Округляя, мы получим 2 заполненные клетки:

   S_озера ≈ 2S_клетки = 8 км²

Задания из ОГЭ

На ОГЭ также встречаются задачи на квадратной решётке, но они построены только на точных вычислениях. Вам могут встретиться задачи на вычисления площади фигур (как в ЕГЭ базового уровня), на нахождение градусной меры угла или элемента фигуры, а также на вычисление тригонометрической функции.

Давайте сосредоточимся на разборе сложных заданий — на их фоне простые покажутся совсем элементарными. 🙂

Углы и тригонометрия

Прежде чем переходить к задачам, советуем повторить темы:

1. Тригонометрия: базовые понятия и формулы.

2. Центральный и вписанный угол в окружности.

3. Теорема Пифагора.

4. Действия с векторами.

Задача 4

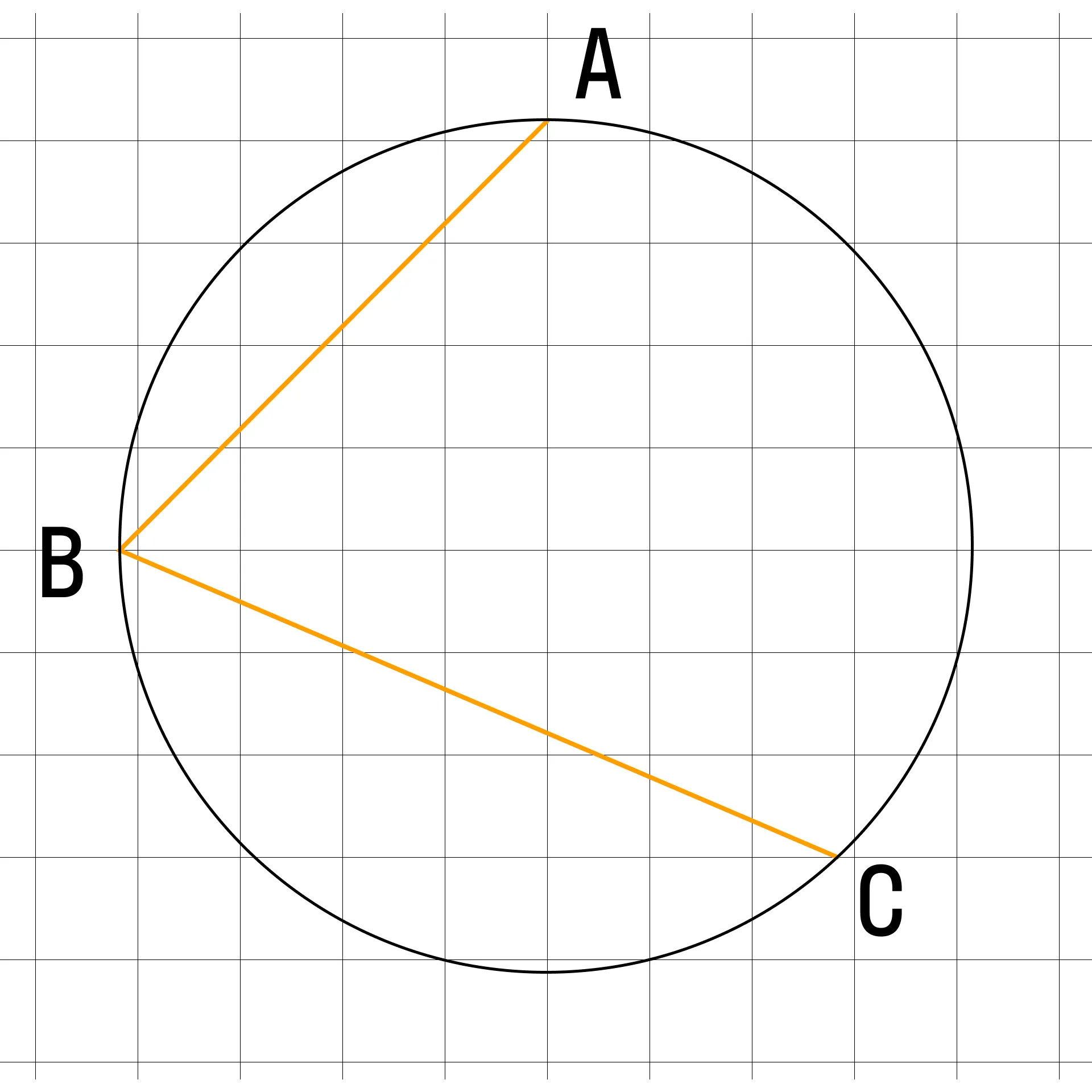
Найдите угол АВС.

Решение

Ключевой подсказкой является то, что угол АВС вписан в окружность. По определению, вписанный угол в два раза меньше центрального, опирающегося на ту же дугу.

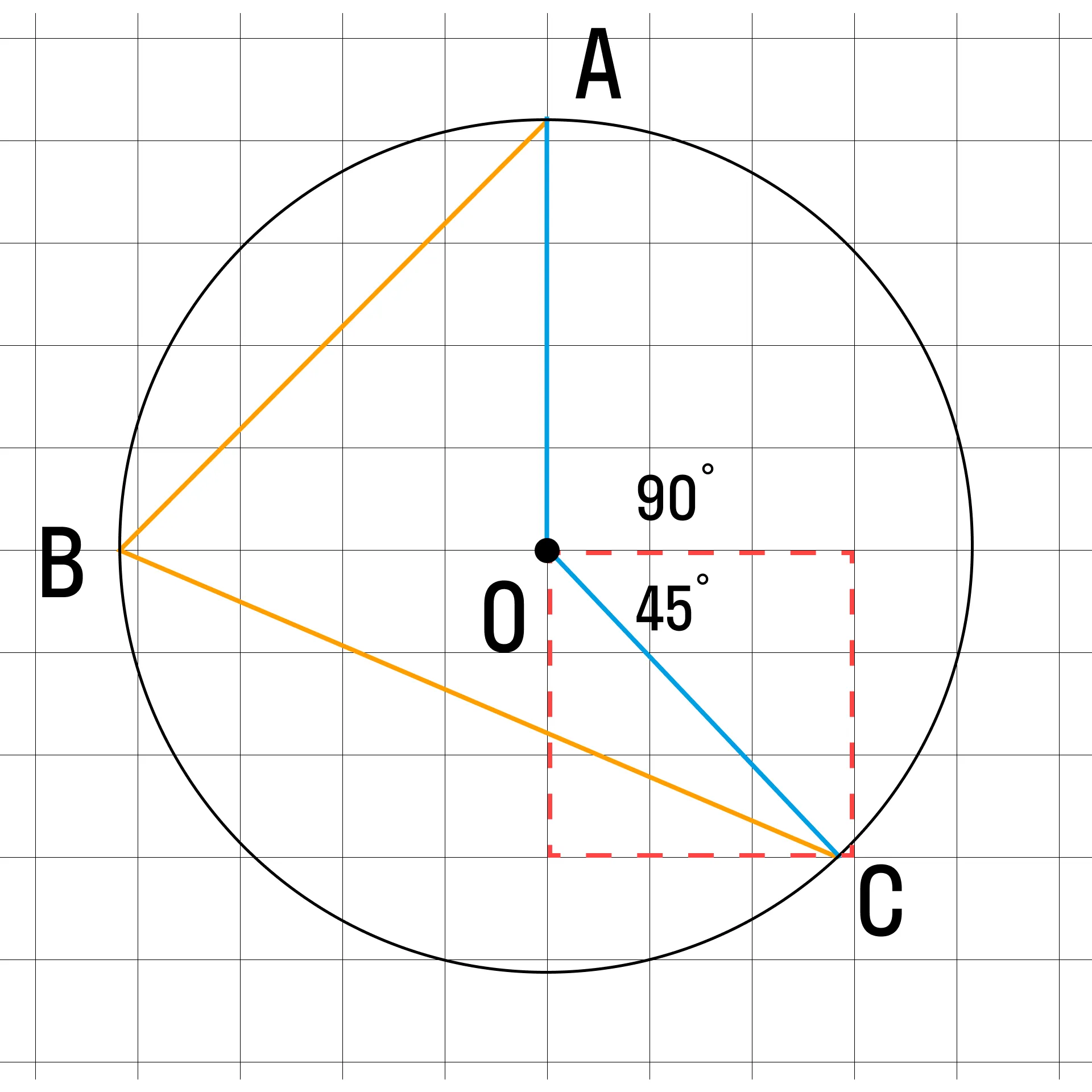
1. Дополнительные построения: найдём центр окружности и построим центральный угол, опирающийся на дугу АС.

   

2. Угол АОС — тупой. Он точно состоит из прямого угла (видно по рисунку) и острого. Чему равен острый угол? Представим, что одна из сторон угла — диагональ четырёхугольника, и дорисуем его. Судя по построениям, этот четырёхугольник — квадрат, а значит, диагональ является биссектрисой прямого угла угол АОС состоит из углов 90° и 45°.

3. Если угол АОС = 90 + 45 = 135, то угол АВС = 1/2 AOC = 135/2 = 67,5.

Задача 5

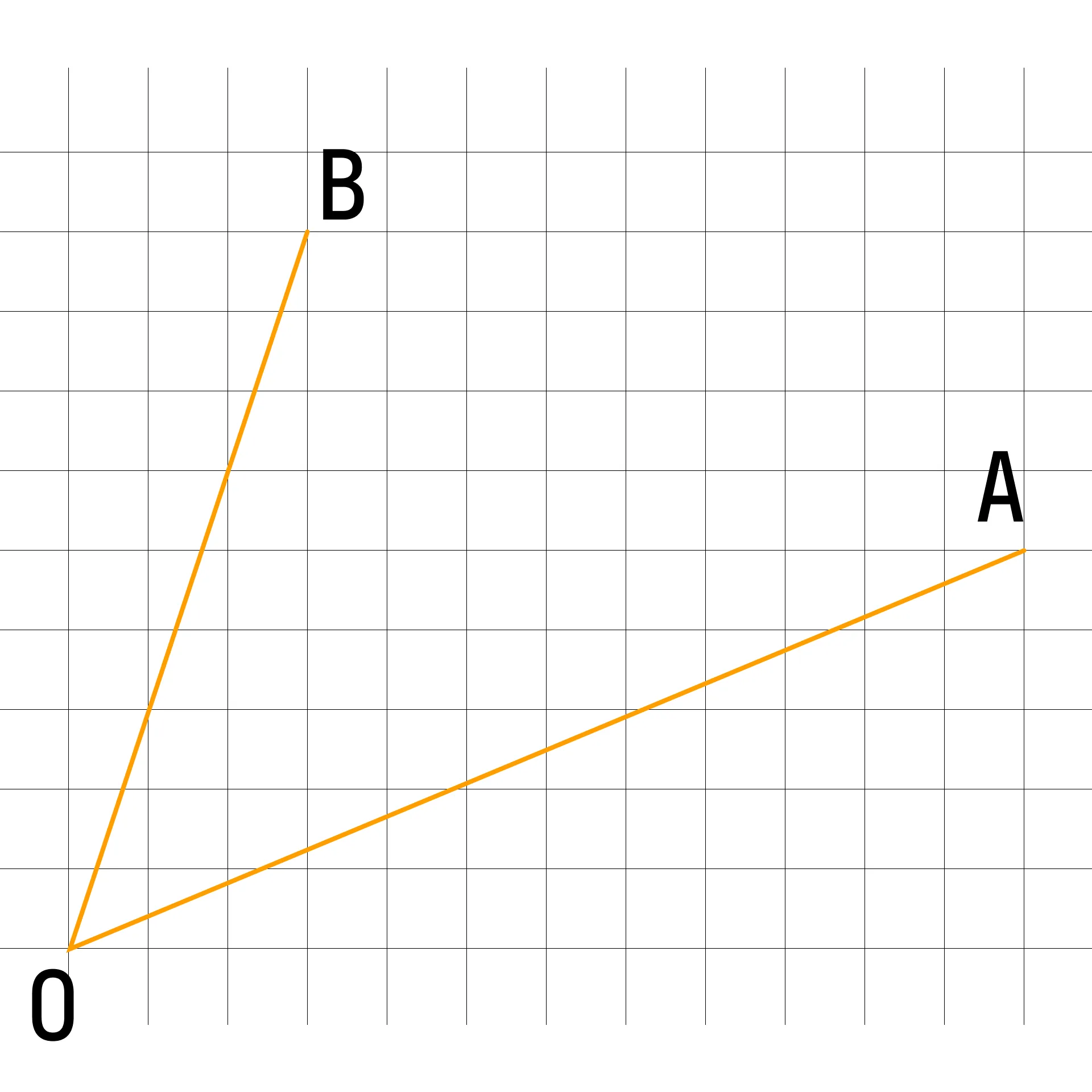
Найдите тангенс угла AOB.

Решение

Эту задачу можно решить двумя методами: через дополнительные построения и определение тангенса или через скалярное произведение векторов. Рассмотрим второй способ.

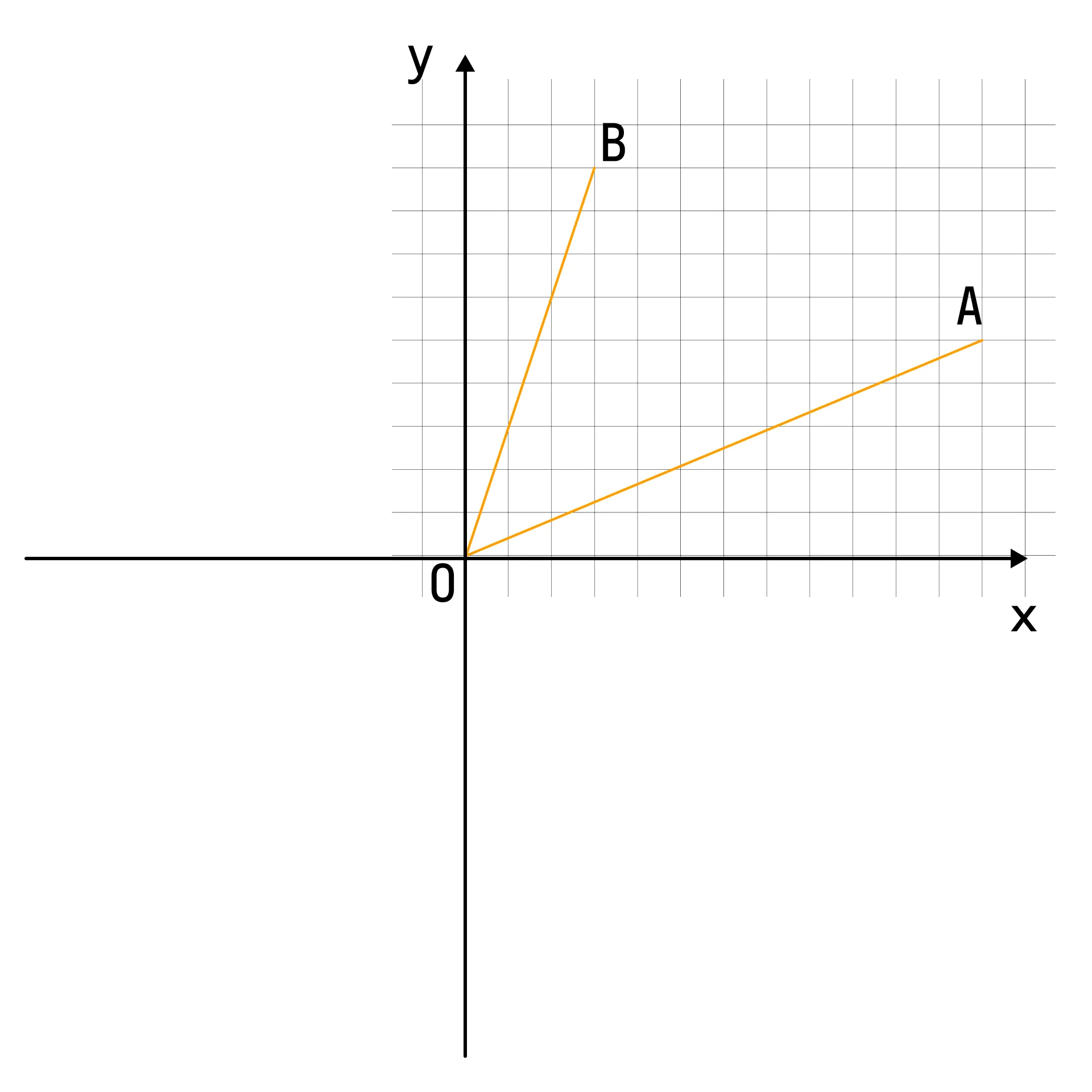
1. Предположим, что точка О — точка начала координат, через неё проходит ось абсцисс и ось ординат.

   

2. Тогда координаты точки А (10; 5), точки В (3; 9).

   Вектор ОА (10; 5); вектор ОВ (3; 9).

3. Найдём длины векторов:

4. Выразим косинус угла между векторами из формулы для скалярного произведения:

Расстояние от точки до прямой

Кратчайшее расстояние от точки до прямой — это перпендикуляр, проведённый из точки на прямую.

Расстояние от точки до точки — это длина отрезка, соединяющего эти точки.

Задача 6

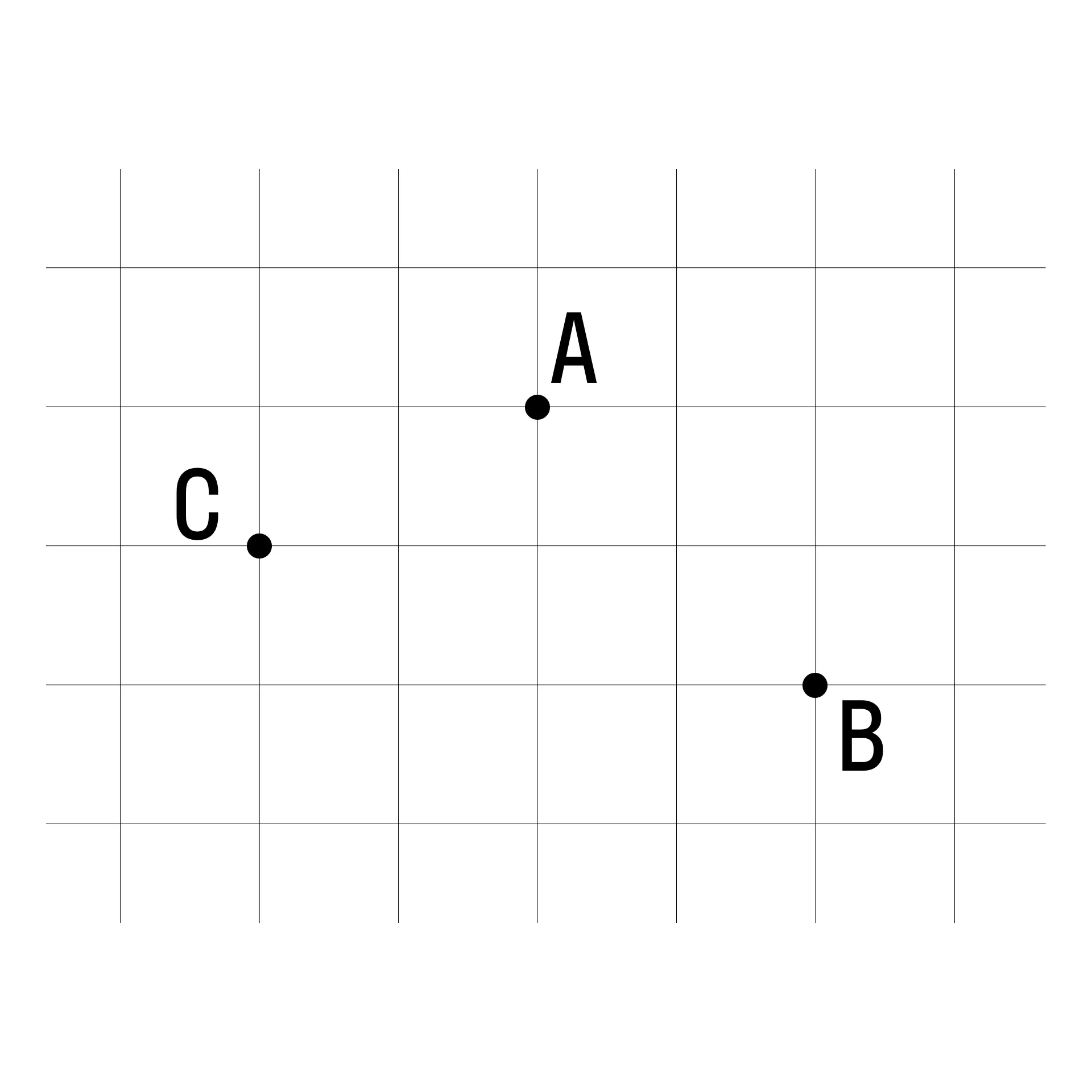
Найдите расстояние от точки А до середины отрезка ВС, если длина клетки равна 2 см.

Решение

1. Найдем середину отрезка ВС. Для этого соединим точки В и С, проведём дополнительные построения: представим, что ВС — это диагональ четырёхугольника, достроим эту фигуру. По построению видно, что полученный четырёхугольник — прямоугольник, а значит, в точке пересечения диагонали делятся пополам достроим вторую диагональ и найдём точку пересечения О.

   

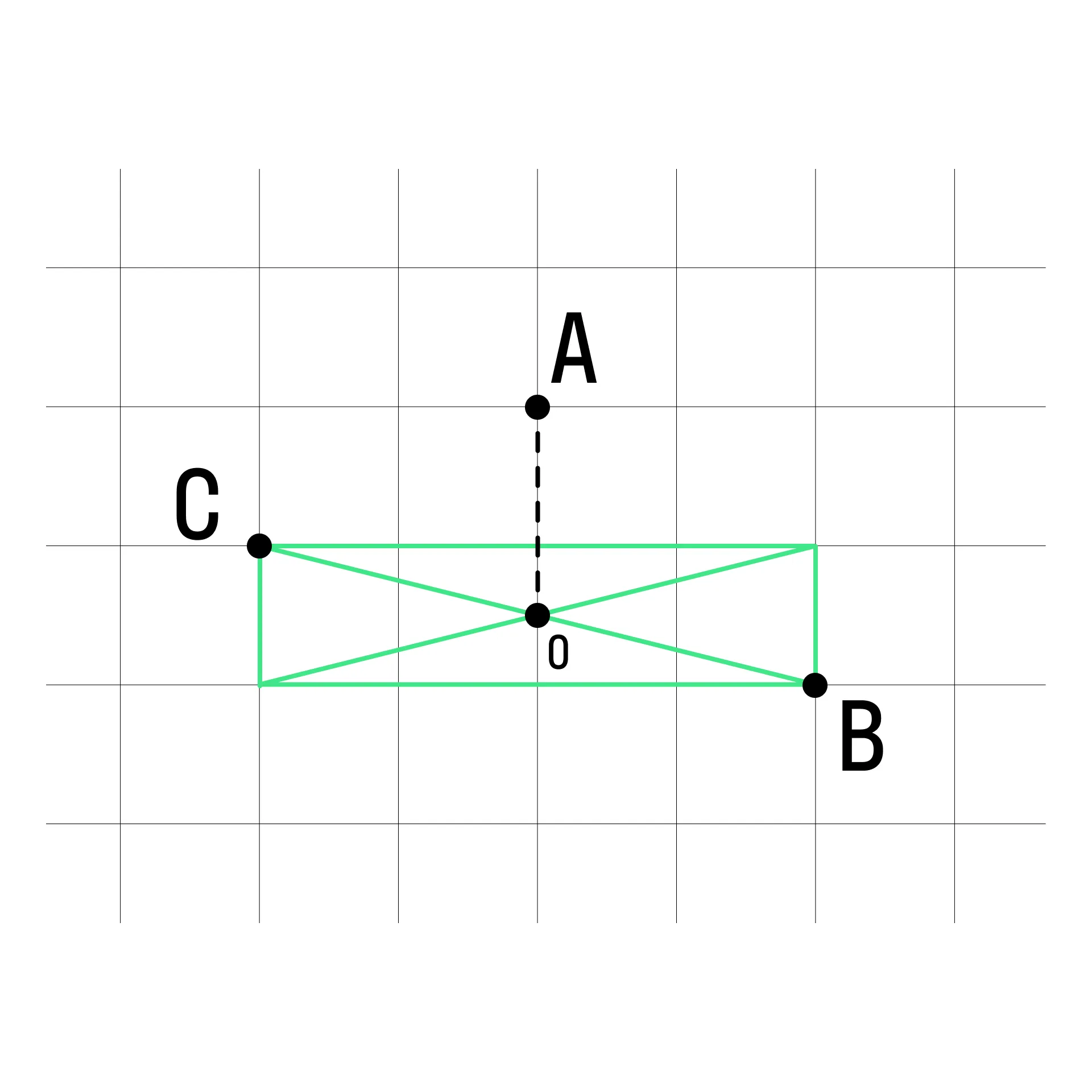
2. Найдём длину отрезка ОА с учётом размера клетки:

   ОА = 1,5 ⋅ 2 = 3 см

Элементы фигур

Чаще всего в задачах такого типа просят найти высоту или среднюю линию фигуры.

• Высоту находим по построению или через теорему Пифагора.

• Средняя линия треугольника равна половине стороны, которой она параллельна.

• Средняя линия трапеции равна полусумме оснований.

Задача 7

Найдите среднюю линию трапеции, если размер клетки 1 × 1 см.

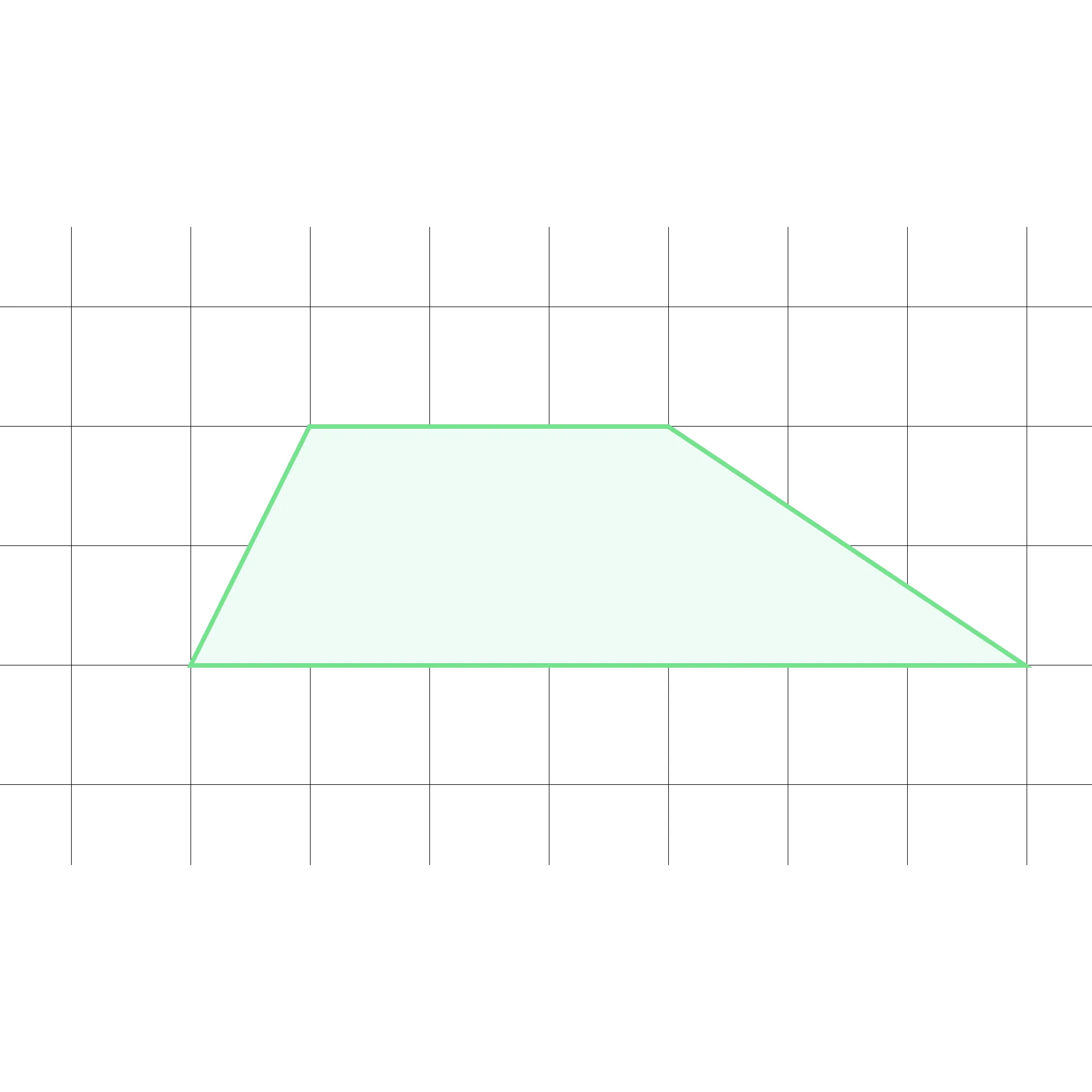
Решение

Для данной задачи невыгодно изображать среднюю линию на рисунке — мы не сможем точно рассчитать её длину. Лучше всего воспользоваться формулой, рассчитав длины оснований:

Чувствуете азарт, хочется решить ещё несколько задач? Тогда скорее переходите по ссылке в бесплатный тренажёр ЕГЭ. Практикуйтесь, решайте, закрепляйте теорию и улучшайте практику. И не забудьте поделиться с друзьями, им тоже будет полезно!