Угол между прямыми

Угол между прямыми на плоскости

Взаимное расположение прямых на плоскости

Когда мы рассматриваем положение прямых на плоскости (в декартовой системе координат XY), они могут:

• быть параллельны друг другу;

• пересекаться (в том числе быть перпендикулярными друг другу);

• совпадать.

Если прямые параллельны друг другу, они никогда не пересекутся, следовательно, у них нет общих точек и они не образуют углы.

Если прямые совпадают, т. е. их будто наложили друг на друга, то у них бесконечное множество общих точек, но между ними по-прежнему не возникает углов.

Если прямые пересекаются, у них есть одна общая точка, и вследствие пересечения образуются 4 угла.

Углы, образованные при пересечении прямых

Углы, входящие в состав одного развёрнутого, называются смежными.

Углы, полученные при пересечении двух прямых и стоящие друг напротив друга, называются вертикальными. Вертикальные углы имеют равную градусную меру.

Так, на рисунке углы 4 и 2, 1 и 3 — вертикальные. Углы 4 и 1, 1 и 2, 2 и 3, 3 и 4 — смежные.

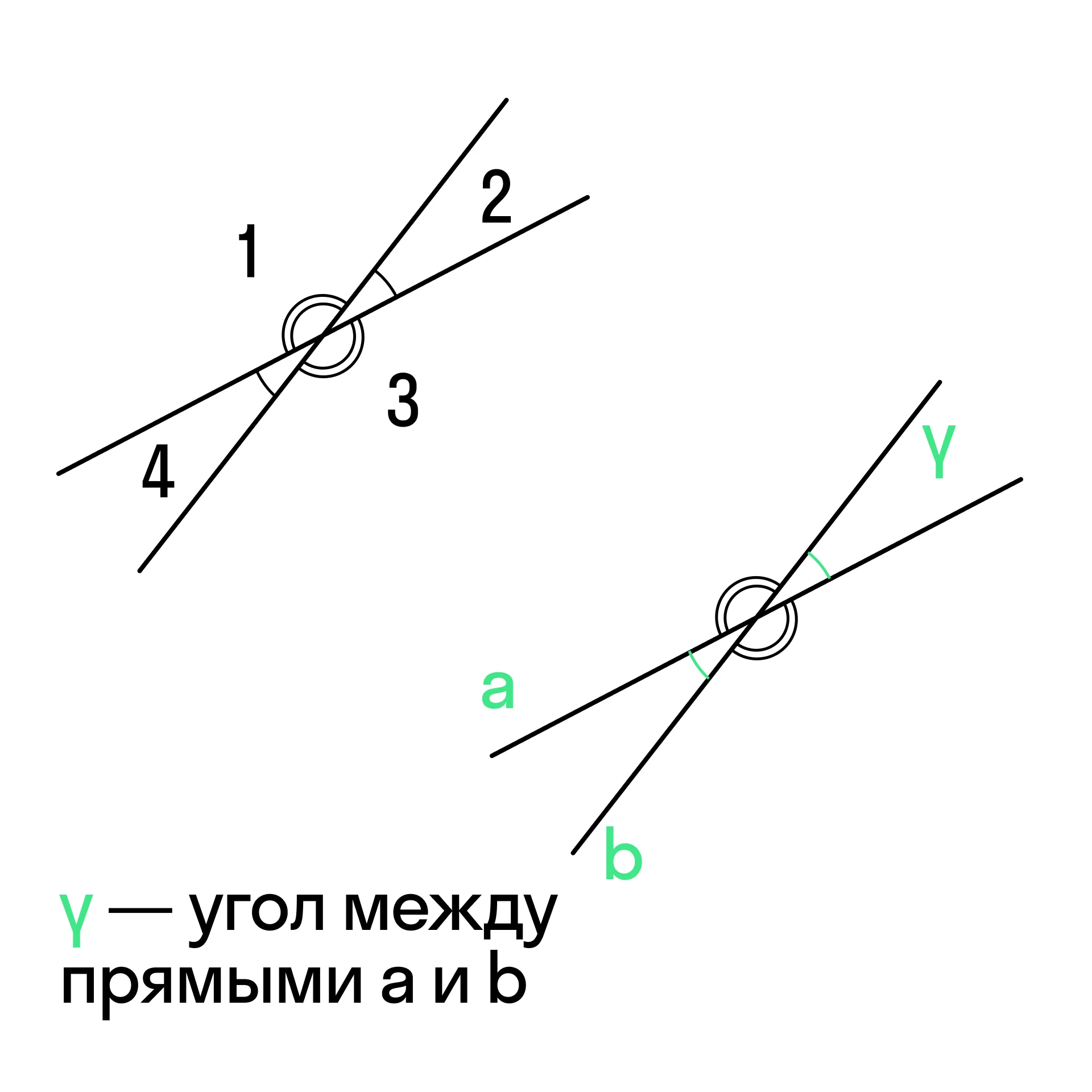
Углом между прямыми принято считать наименьший угол (острый). В случае, если прямые пересекаются под углом 90°, т. е. прямые перпендикулярны друг другу, за угол между прямыми можно считать любой из прямых углов.

Как найти угол между двумя прямыми на плоскости

1. Если вам необходимо найти угол между прямыми по рисунку (чертежу), достаточно знать любой из углов, полученных при пересечении прямых. Если известный угол острый, он и будет считаться углом между прямыми. Если известный угол тупой, необходимо найти значение смежного с ним угла.

   Задача 1

   При пересечении прямых a и b был получен угол, равный 110°. Найдите угол между прямыми.

   

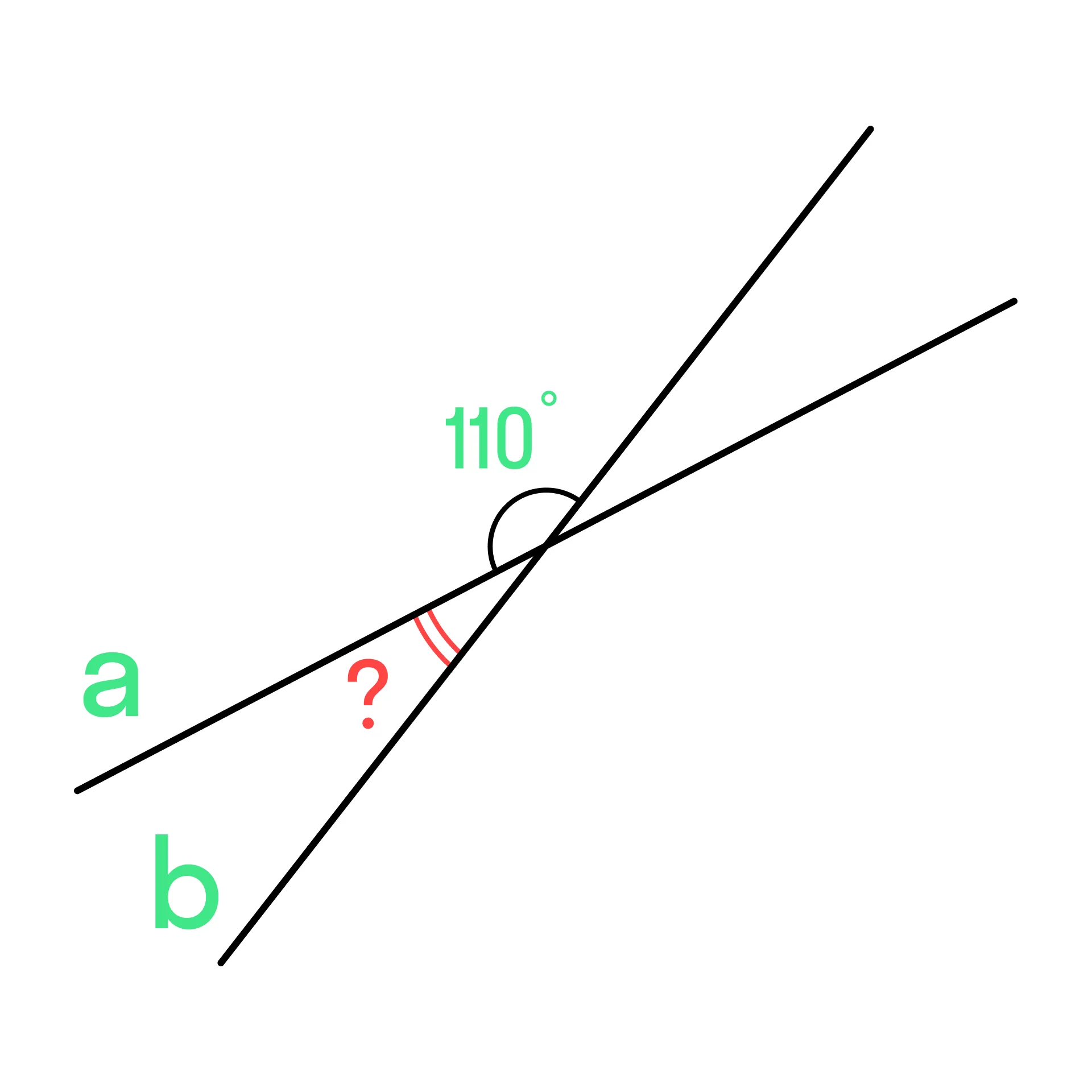
   Мы видим, что известный угол — тупой. Найдём смежный с ним: φ = 180 − 110 = 70°.

2. Если прямые заданы с помощью уравнения y = kx + b, необходимо воспользоваться формулой:

   Таким образом вы найдёте тангенс угла (и этого часто достаточно для ответа).

   Если же в задании необходимо дать точное значение угла, можно воспользоваться таблицей Брадиса, где каждому значению тригонометрической функции сопоставлено значение соответствующего угла.

   Важно: по значению угловых коэффициентов k можно заранее проверить, являются ли прямые перпендикулярными или параллельными:

   • если коэффициенты k у прямых равны, прямые являются параллельными;

   • если k₁ ⋅ k₂ = −1, прямые перпендикулярны.

   Задача 2

   Найдите угол между прямыми, заданными уравнениями: и .

   Определим угловые коэффициенты: .

   Так как коэффициенты не равны, прямые не параллельны друг другу и не перпендикулярны, так как .

   Подставим значения в формулу:

   Если вас смущает запись арктангенса arctg и вы не знаете, что она означает — приходите на уроки математики в онлайн-школу Skysmart. Мы научим вас уверенно работать со всеми тригонометрическими функциями, подготовим к любым экзаменам и вернём любовь к математической науке!

3. Если прямые заданы через векторы, то можно воспользоваться формулой для вычисления скалярного произведения векторов, выразив оттуда косинус угла между векторами:

   

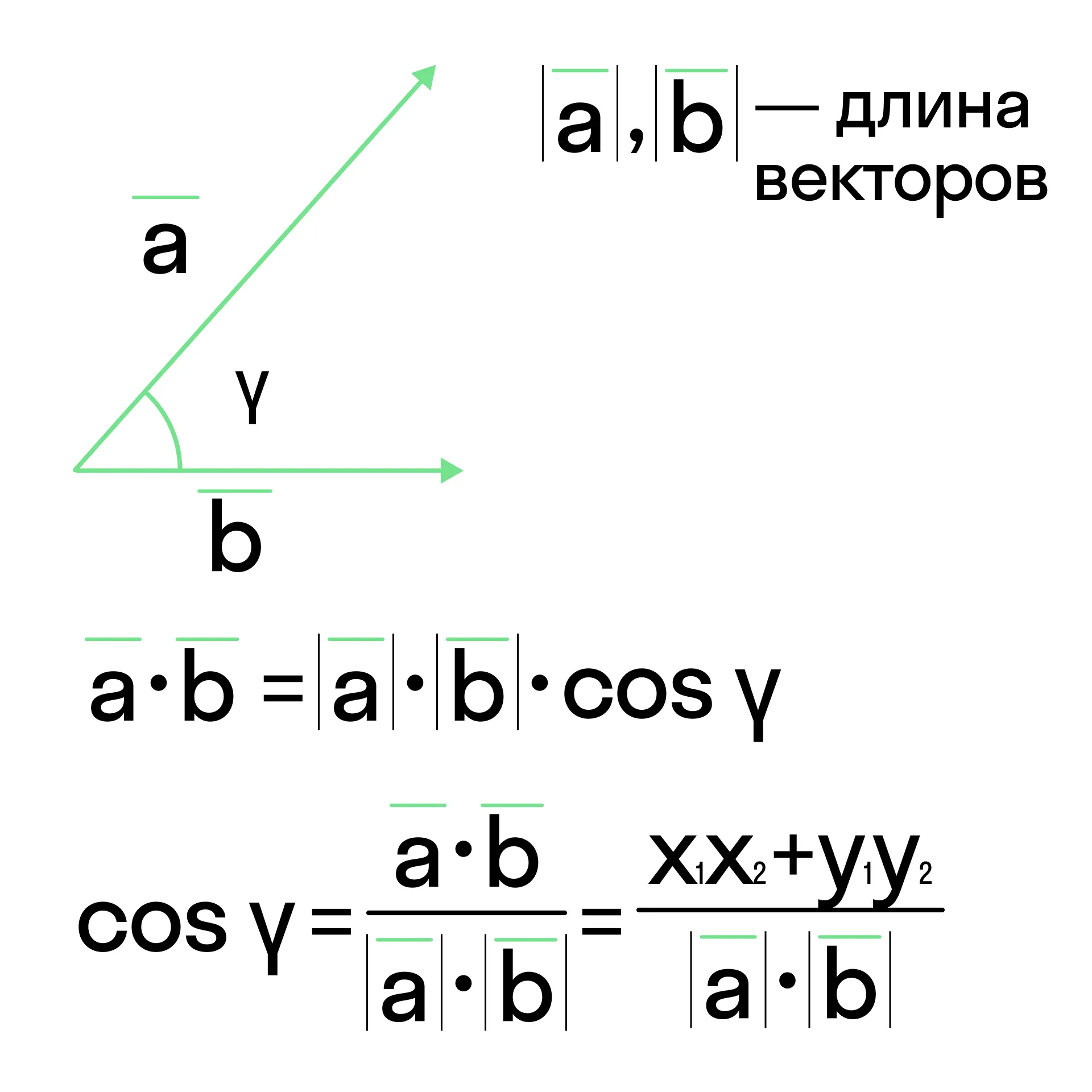
   Задача 3

   Найти угол между векторами a (−1; 0) и b (3; −2), если их длины соответственно равны 2 и 5.

   Ответ:

Угол между прямыми в пространстве

Взаимное расположение прямых в пространстве

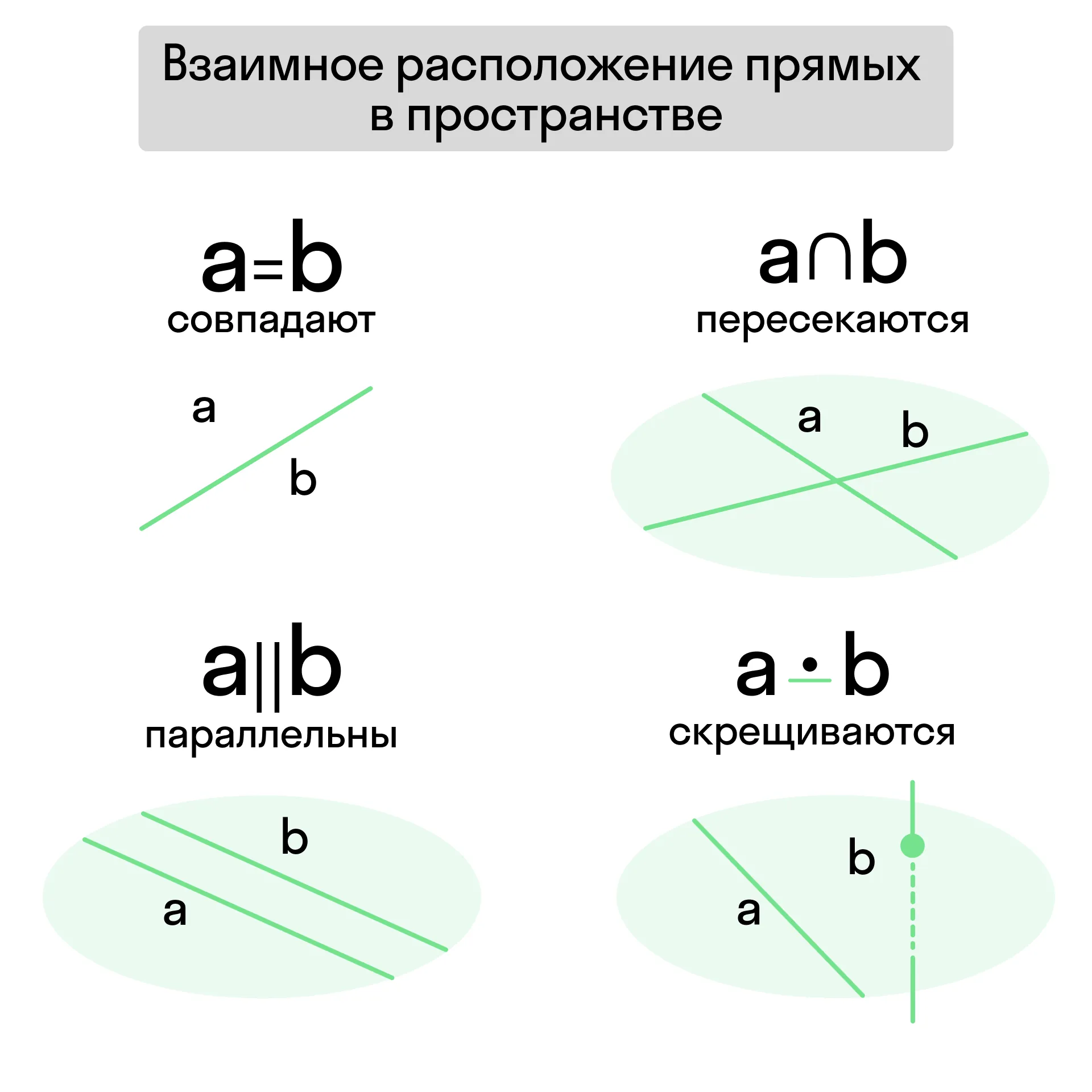
Если мы рассматриваем расположение прямых в пространстве, для этого случая справедливы все вышеперечисленные варианты: прямые могут совпадать, быть параллельными и пересекаться. Помимо этого, возможен ещё один случай — прямые могут быть скрещивающимися.

Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Представьте себе коробку (параллелепипед). Обозначим некоторые из её рёбер.

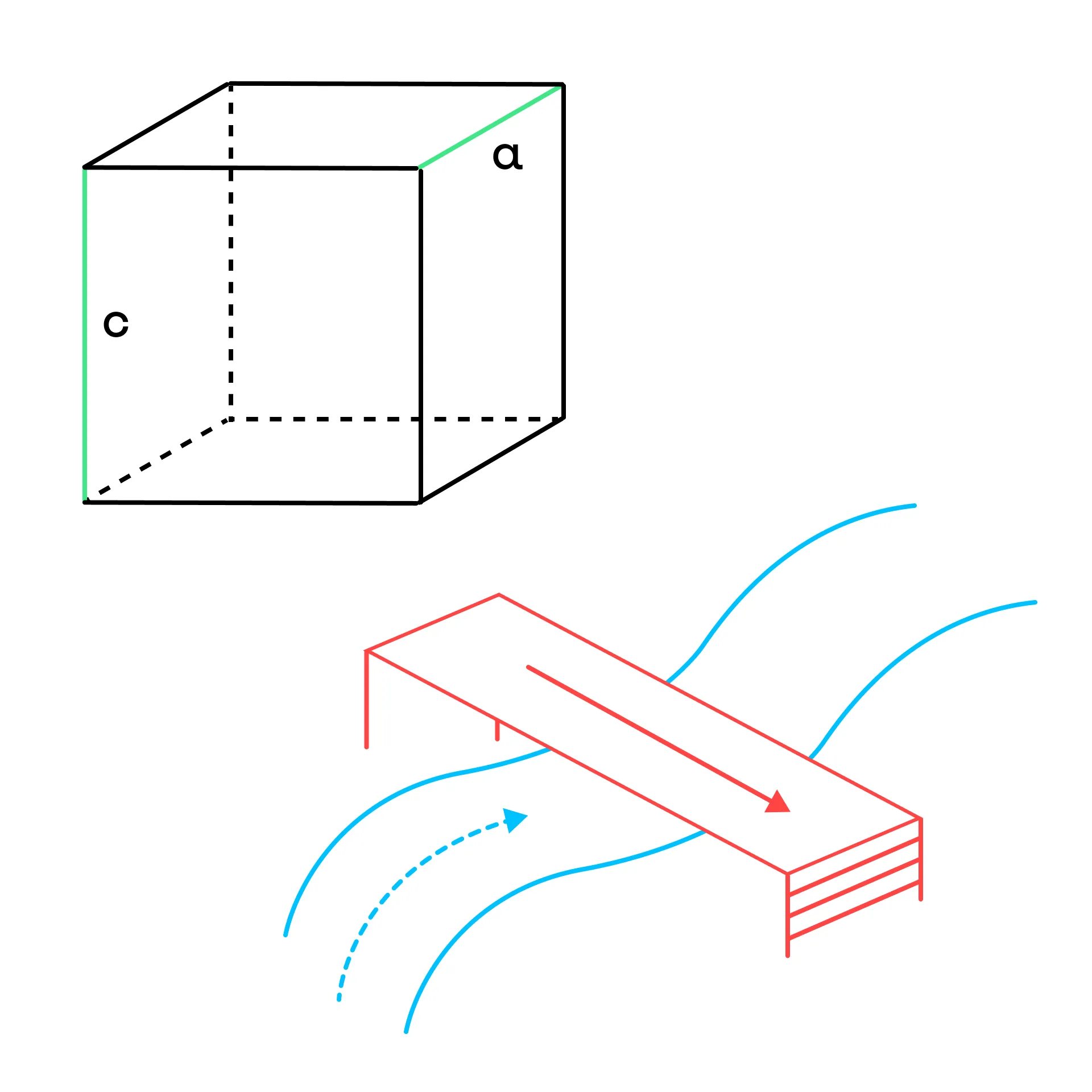
Рёбра с и d лежат в разных плоскостях и чисто физически никаким образом друг друга не касаются, не имеют общих точек, они не параллельны друг другу. Но если бы мы каким-то образом смогли приблизить их друг к другу, они могли бы пересечься.

Или представьте мост, нависающий над рекой. Дорога по мосту и по реке не пересекаются, не параллельны друг другу — мы физически можем проплыть под мостом по реке или перейти мост и увидеть людей, проплывающих внизу.

Угол между скрещивающимися прямыми

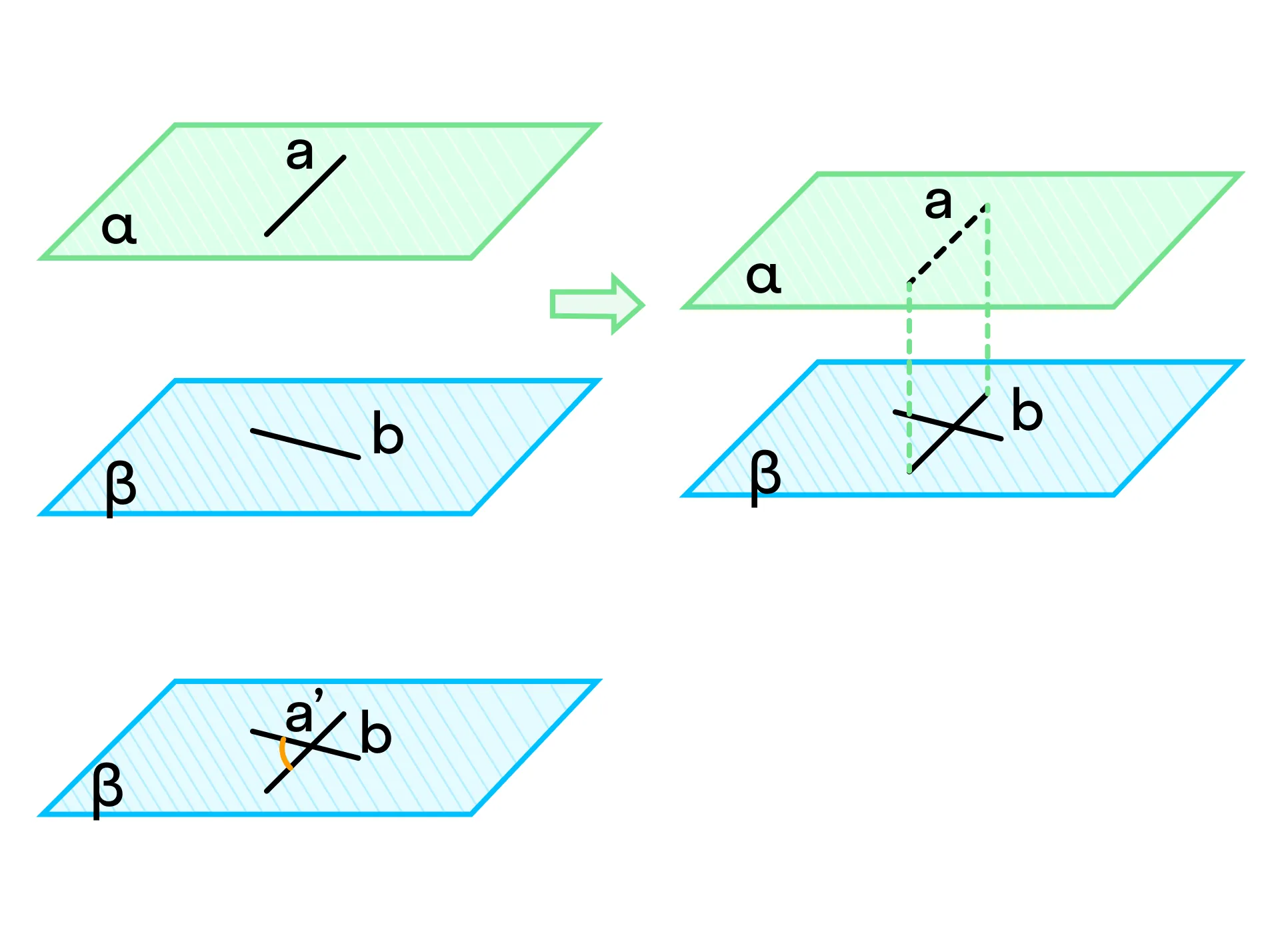
Мы можем рассчитать угол между скрещивающимися прямыми. Для этого:

1. Мы должны знать, что через каждую из двух скрещивающихся прямых можно провести плоскость, параллельную второй прямой, и только одну.

2. Параллельным переносом перенесём одну прямую на плоскость, содержащую вторую прямую.

3. Найдём угол между этими прямыми.

   

Чтобы закрепить пройденный материал и ещё лучше понять тему на практике, воспользуйтесь нашим бесплатным тренажёром ЕГЭ. Это лёгкий и полезный инструмент, который пригодится вам не только для подготовки к контрольным работам, но и для углубления знаний и расширения математического кругозора!