Расстояние от точки до прямой

Что называется расстоянием от точки до прямой?

Расстояние от точки до прямой — это длина перпендикуляра, опущенного из данной точки на прямую. Перпендикуляр — это кратчайшее расстояние от точки до прямой.

Доказать это очень просто. Из точки M на прямую f мы опустим перпендикуляр MN и произвольную прямую MP, которая также называется наклонной. А по свойству мы помним, что наклонная всегда больше перпендикуляра, что и требовалось доказать.

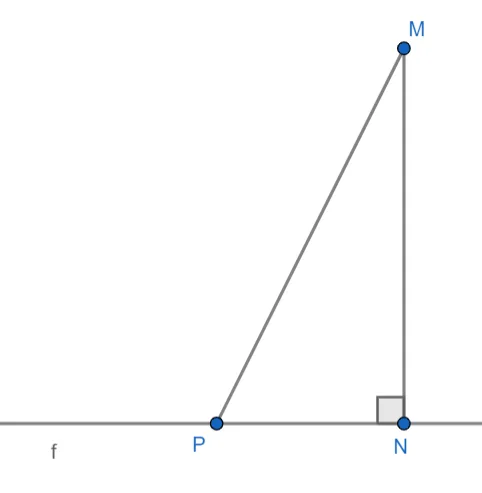
Расстояние между точкой M и прямой f на плоскости обозначают так:

Расстояние между параллельными прямыми

А если нужно вычислить расстояние между двумя параллельными улицами — какое математическое понятие поможет в этом случае? Конечно, вы уже догадались, что это расстояние между параллельными прямыми.

Расстоянием между параллельными прямыми называется расстояние от какой-либо прямой до другой прямой на плоскости.

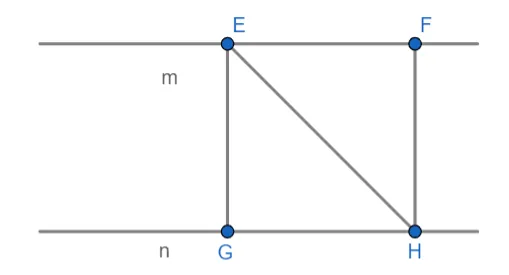
Убедимся в верности этого утверждения — рассмотрим параллельные прямые m и n. На прямой m выберем две точки E и F, опустим из них перпендикуляры на прямую n, точки пересечения перпендикуляров с прямой n обозначим буквами G и H, а также соединим E и H отрезком.

Рассмотрим треугольники GEH и EFH: сторона EH — общая, (как накрест лежащие углы). Следовательно, по гипотенузе и острому углу. А из свойства равных треугольников мы знаем, что будут равны и соответствующие элементы, например, EG = FH.

Делаем вывод, что расстоянием между параллельными прямыми на плоскости является длина их общего перпендикуляра, причем выбор перпендикуляра может быть произвольным.

Расстояние между двумя прямыми m и n обозначается так: .

179.6K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Решение задач

Применим полученные знания, решив несколько задач.

Задача 1

На клетчатой бумаге с размером клетки отмечены точки K, M и N. Чему равно расстояние от точки K до прямой MN?

Как вы помните, чтобы найти расстояние от точки до прямой, нужно из точки на прямую опустить перпендикуляр и вычислить его длину.

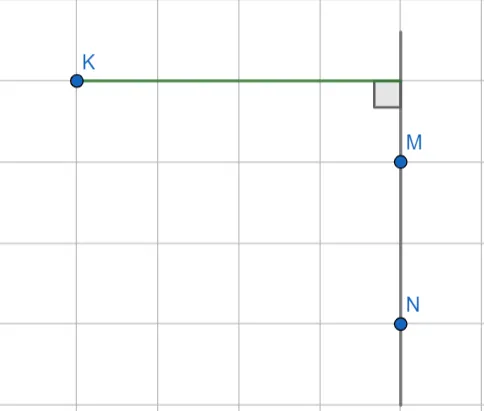
Ответ: 4 см.

Задача 2

Найдите расстояние от точки Q до прямой PR, пользуясь данными с чертежа.

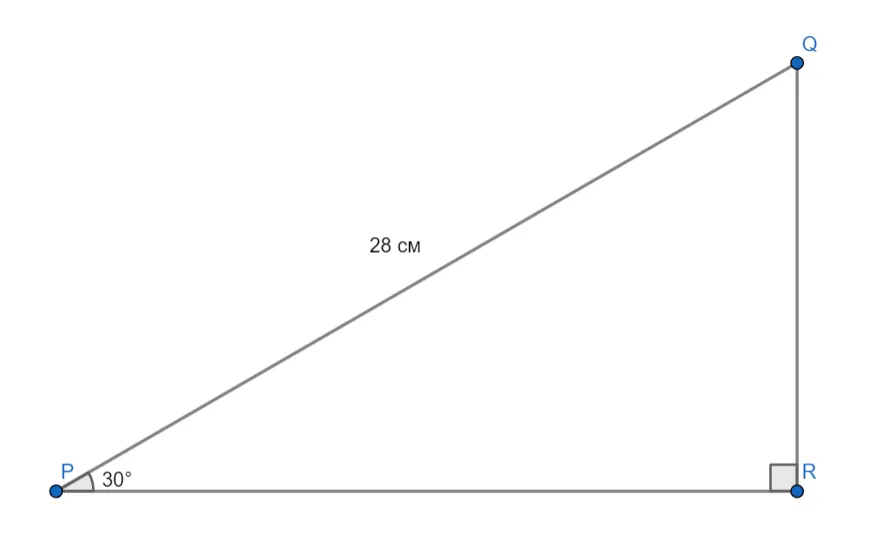
Из чертежа видно, что отрезок QR перпендикулярен прямой PR, а значит QR — расстояние от точки Q до прямой PR. В прямоугольном треугольнике PQR отрезок QR лежит против угла в , а значит, равен половине гипотенузы, то есть 14 см.

Ответ: 14 см.

Задача 3

В равностороннем треугольнике PQR проведена биссектриса QS, а ST — расстояние от точки S до прямой QR, равное 12 см. Чему равно расстояние от точки Q до прямой PR?

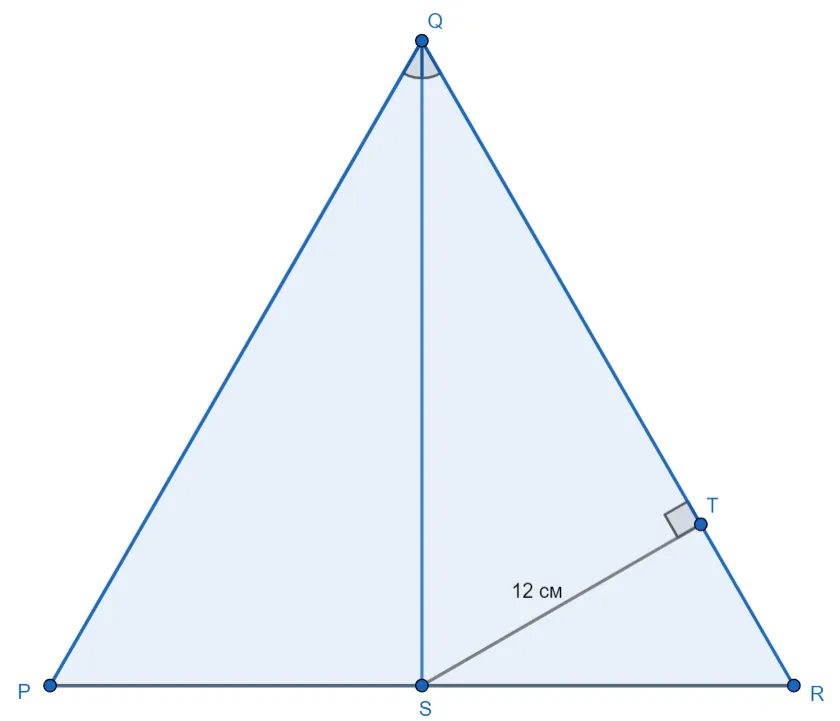
1. Поскольку — равносторонний, то , а так как по условию QS — биссектриса, то .

2. Рассмотрим , так как ST — расстояние от точки S до прямой QR, значит, — прямоугольный. А ST — катет, лежащий против угла в , следовательно, QS = 2ST = 24 см.

3. Так как — равносторонний, то QS не только биссектриса, но и высота , значит, .

Ответ: 24 см.

А если прямая на плоскости находится так далеко, что провести до нее перпендикуляр физически не получается — что делать в этом случае? Поможет формула расстояния от точки до прямой в координатах.

Пусть формула задана прямой f: ax + by + c = 0 и есть точка M с координатами , тогда формула расстояния от точки до прямой на плоскости выглядит следующим образом:

.

Задача 4

Найдите расстояние от точки M (36; 6) до прямой f: 6x + 2y − 12 = 0.

Нам не придется даже изображать прямую и точку, а тем более подбирать масштаб, чтобы поместился перпендикуляр, — достаточно воспользоваться формулой:

Конечно, без координат тоже можно вычислить, но вариант выше — самый рациональный и удобный.

На курсах по математике в онлайн-школе Skysmart мы всегда показываем разные способы решений, которые сохранят вам время на контрольной или экзамене. Выберите подходящий по уровню и цели обучения курс и начните заниматься в удовольствие!