Вычитание дробей

Для кого эта статья:

• Ученики и студенты, изучающие математику
• Родители, желающие помочь детям с математическими задачами
• Учителя, разрабатывающие учебные материалы по математике

Понятие дроби

Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Есть два формата записи:

• обыкновенный вид — или ,
• десятичный вид — 0,5.

Над чертой принято писать делимое, которое является числителем. А под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

1. Числовые — состоят из чисел, например, или .

2. Алгебраические — состоят из переменных, например, . В этом случае значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например и .

Неправильной — такую дробь, у которой числитель больше знаменателя или равен ему. Например, . Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — .

Основные свойства дробей:

1. Дробь не имеет значения, если знаменатель равен нулю.

2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

3. Равными называют и в том случае, если a × d = b × c.

4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!

Вычитание дробей с одинаковыми знаменателями

Для вычитания дробей с одинаковыми знаменателями нужно от числителя первой отнять числитель второй, а знаменатель оставить тот же.

Прежде, чем зафиксировать ответ, важно проверить возможность сокращения.

Рассмотрим это правило на примере:

Получи больше пользы от Skysmart:

• Прокачивай знания на курсах математики

• Выбирай из 1200+ репетиторов по математике

• Записывайся на бесплатные курсы для детей

Вычитание дробей с разными знаменателями

Как вычитать дроби с разными знаменателями? Для этого приводим их к общему знаменателю и находим разность числителей.

Рассмотрим пример, в котором нужно найти разность и .

Как решаем:

• Первым делом нам нужно привести дроби к общему знаменателю. Для определения единого знаменателя понадобится найти наименьшее общее кратное — НОК.

• Чтобы найти НОК, раскладываем знаменатели 9 и 15 на простые множители:

  9 = 3 × 3

  15 = 3 × 5

• Сначала выпишем множители из первого разложения: 3 × 3. Теперь добавим множитель из второго разложения, которого не было в первом — это 5. Перемножаем и получаем НОК:

  НОК (9, 15) = 3 × 3 × 5 = 45

• Найдем дополнительные множители. Для этого НОК делим на каждый знаменатель:

  45 : 9 = 5

  45 : 15 = 3

• Полученные числа умножим на соответствующие дроби:

  и

• Перейдем к вычитанию заданных чисел:

  

Ответ:

Вычитание обыкновенной дроби из натурального числа

Для вычитания из обыкновенной дроби натурального числа необходимо это действие привести к вычитанию обыкновенных дробей.

Разберем для наглядности пример разности 3 и .

Как решаем:

• Представим натуральное число в виде смешанного — займем единицу и переведем ее в неправильную дробь с тем же знаменателем, что у вычитаемой:

  .

• Вычтем одну дробь из другой:

Ответ: две целых одна седьмая.

Вычитание натурального числа из обыкновенной дроби

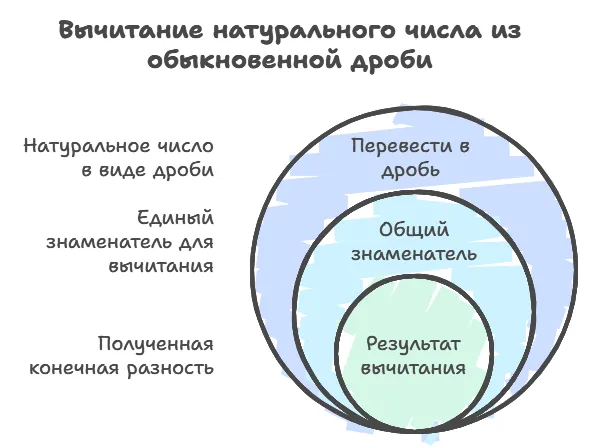
Для вычитания натурального числа из обыкновенной дроби нужно последовать тому же алгоритму, что и в предыдущем примере. А именно: перевести натуральное число в вид дроби, привести все к единому знаменателю, найти разность.

Рассмотрим пример разности и 3.

Как решаем:

А еще можно вот так:

• Представим в виде смешанной дроби, для этого разделим делитель на делимое:

• Произведем вычитание: