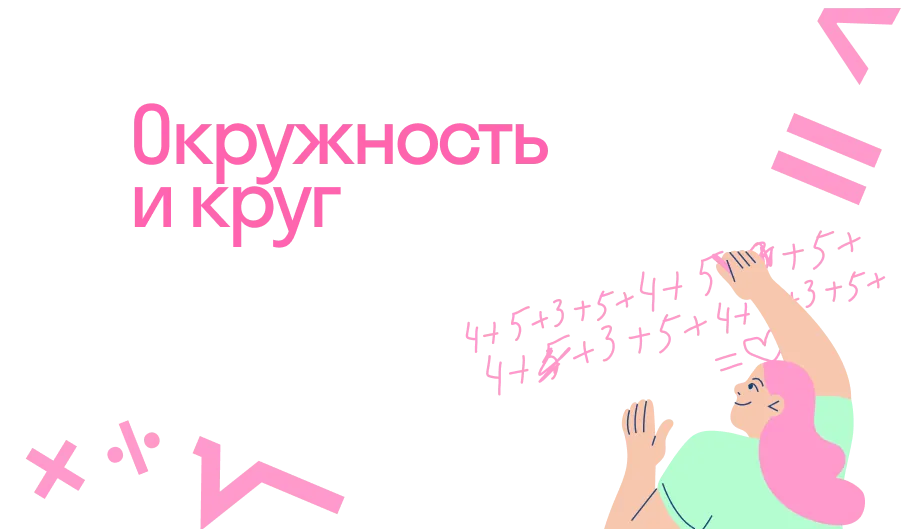Окружность и круг: формулы и свойства

Окружность и круг — определения

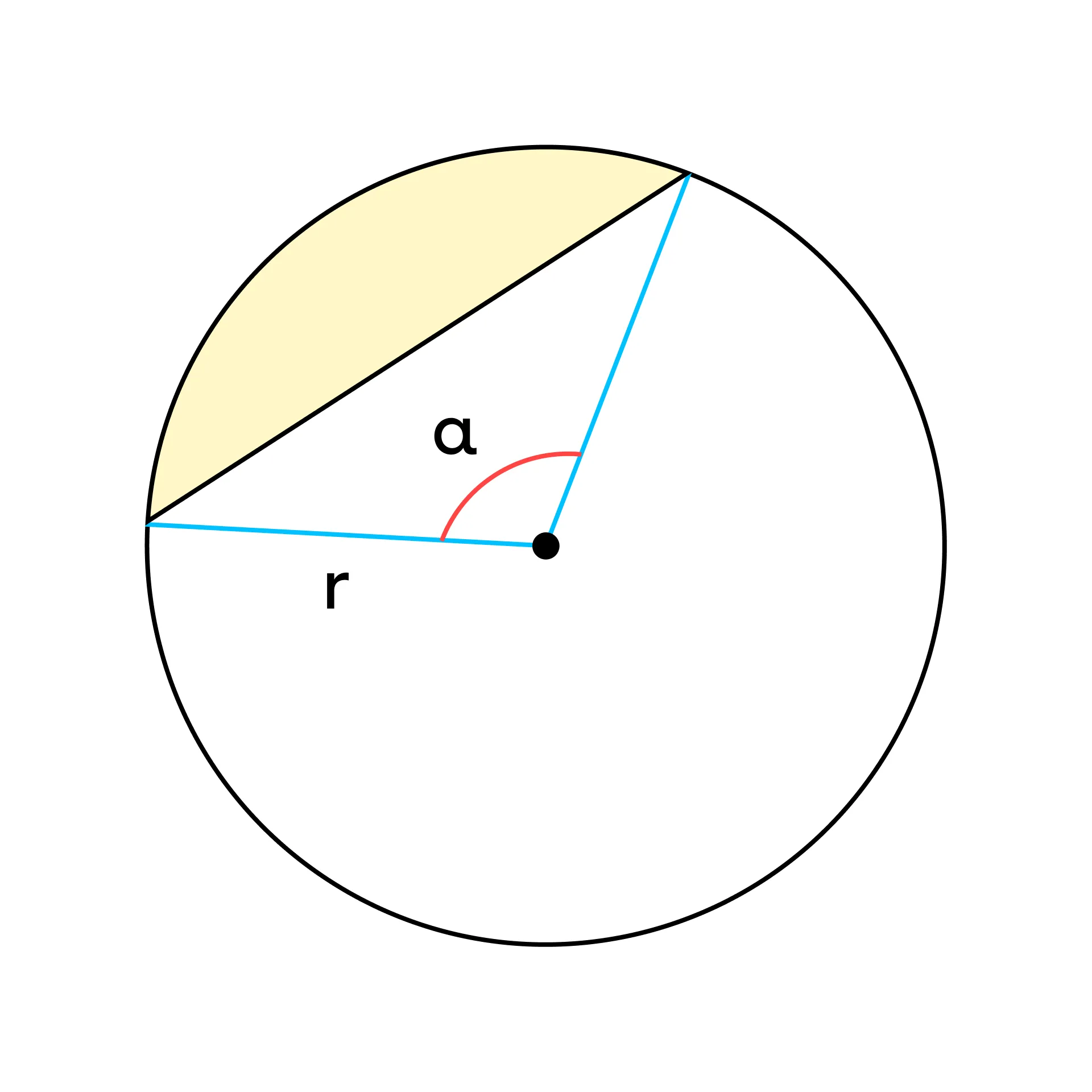
Окружность — это замкнутая кривая, все точки которой равноудалены от её центра.

Круг — геометрическая фигура, ограниченная окружностью.

Чтобы разница между фигурами стала более понятной, представьте следующие примеры: окружность — бублик, круг — ватрушка или окружность — забор вокруг поля, круг — само поле. Как вы могли заметить, круг представляет собой заполненную фигуру, в то время как окружность — это по сути круглая рамка.

И хотя у этих понятий есть чёткие различия, значения их элементов полностью совпадают (и у окружности, и у круга есть центр, диаметр, радиус и т. д.).

Радиус и диаметр окружности

Радиус окружности — отрезок, соединяющий центр окружности с точкой на окружности. В одной окружности можно провести бесконечное количество радиусов и все они будут равны между собой.

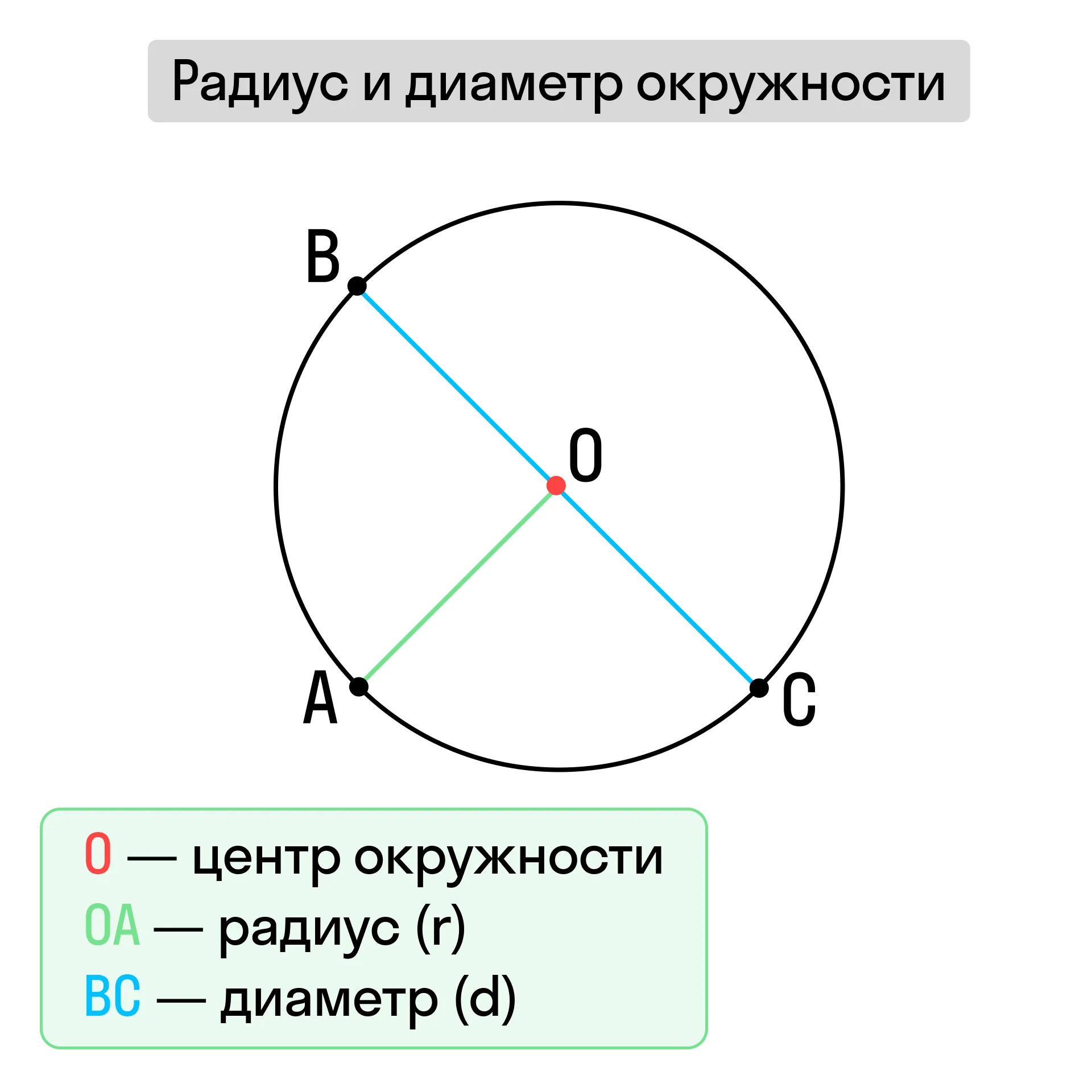
Радиус обозначается с помощью сочетания букв, например OA, OB, OC, где О — центр окружности, а точки А, В и С лежат на окружности.

273.1K

Как найти радиус окружностиЧитать →

Для обозначения радиуса вписанной окружности чаще всего используют маленькую букву r, а для описанной окружности — заглавную R, в остальных же случаях вы можете выбирать между строчной и заглавной буквой по своему усмотрению.

Диаметр окружности — это отрезок, соединяющий две точки на окружности и проходящий через её центр. Также как и в случае с радиусами, в окружности можно провести бесконечное количество диаметров.

Диаметр может обозначаться буквами d или D, а также через сочетания букв (например AB, CD и т. д., при этом не нужно называть и точку центра окружности, которая лежит на этом отрезке).

463.6K

Как найти диаметр окружности: формулы и калькуляторЧитать →

В один диаметр умещается два радиуса D = 2r, или радиус окружности равен половине её диаметра r = 1/2 D.

178.1K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Хорда окружности и её свойства

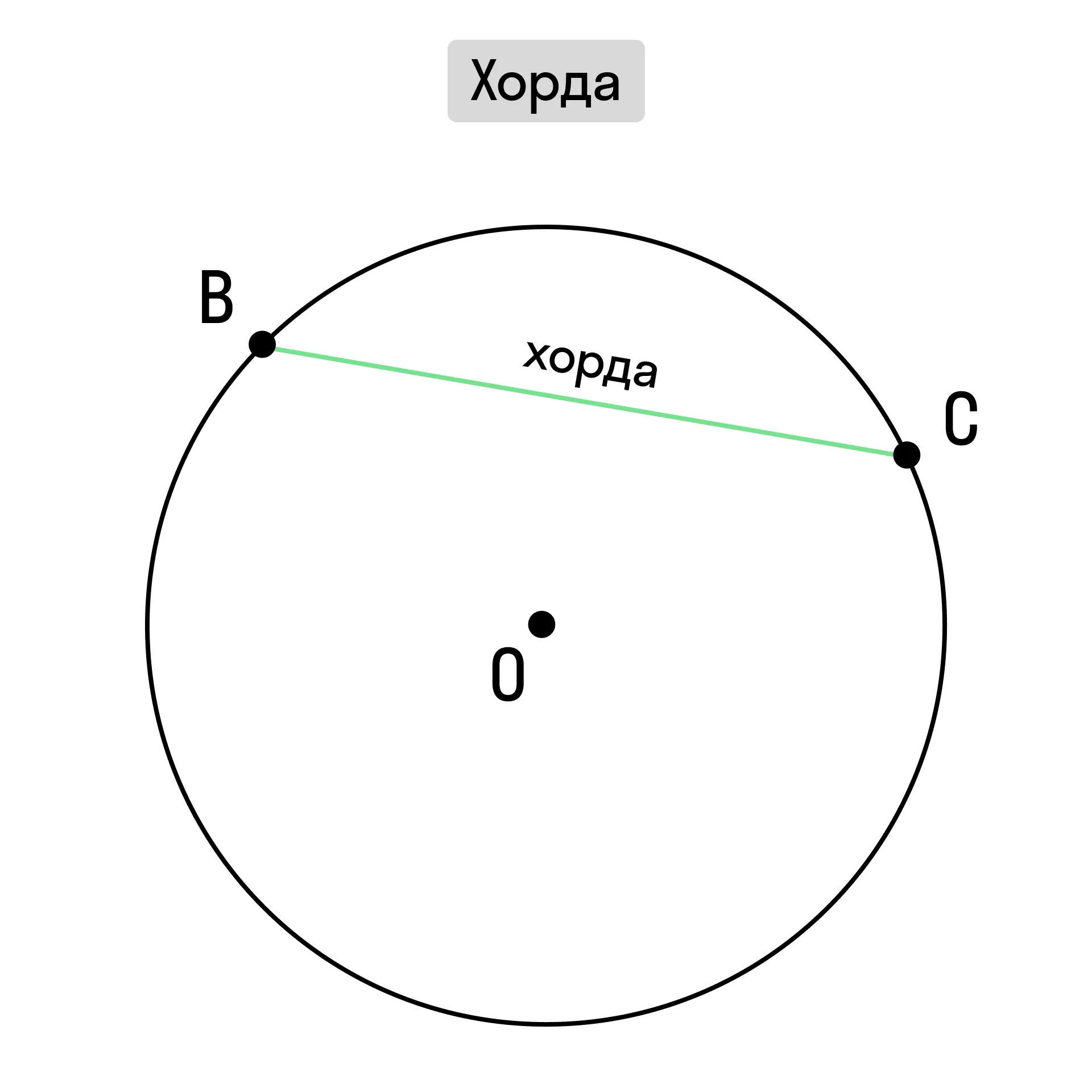
Хорда — отрезок, соединяющий две точки окружности.

Для хорды нет какого-то особенного обозначения, её называют по точкам, которые она соединяет.

Это интересно

Чисто технически диаметр окружности является её хордой, так как по определению это отрезок, соединяющий две точки окружности. Но запомните: любой диаметр является хордой, но не любая хорда — это диаметр.

Свойства хорды:

1. Диаметр, перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам.

   

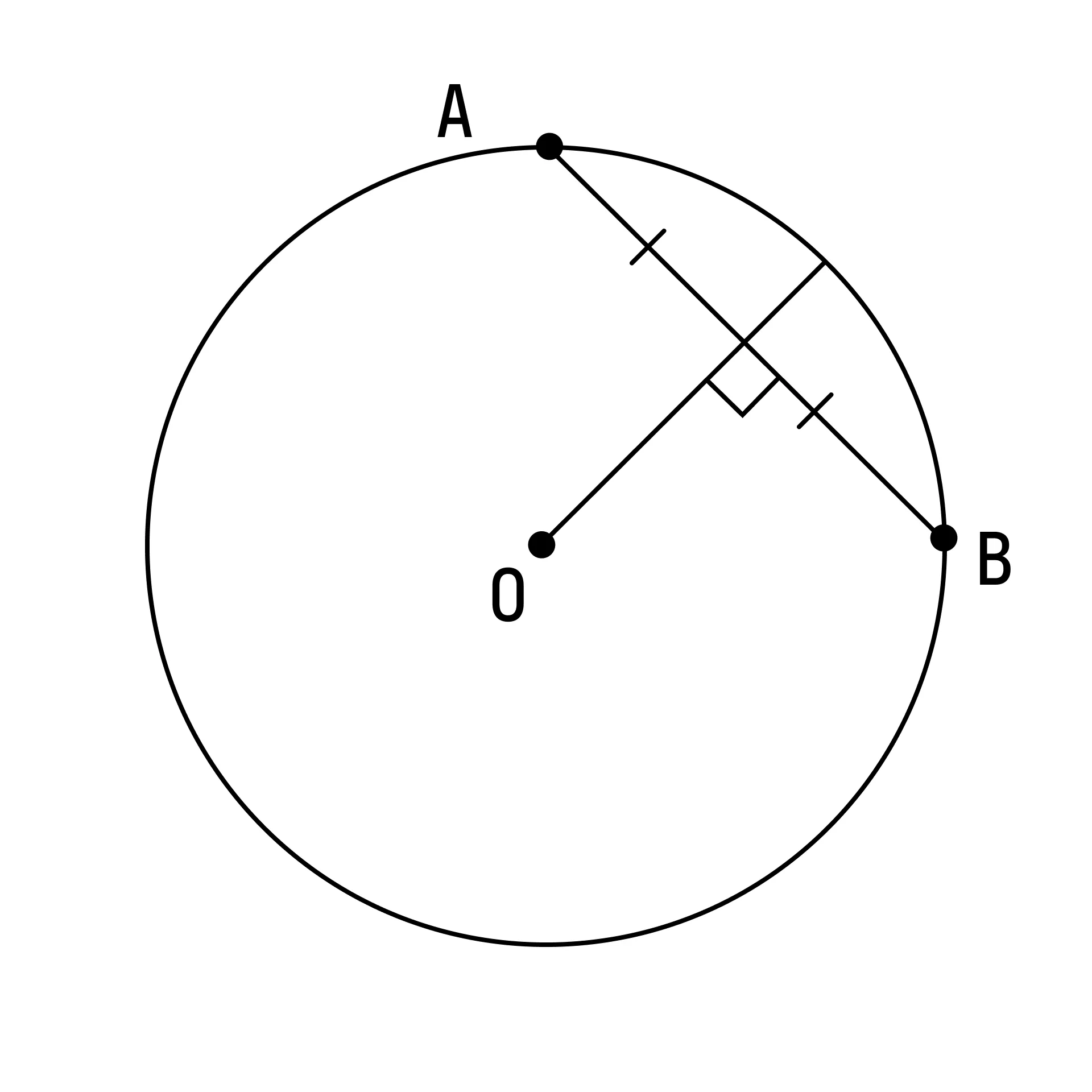
2. Дуги, заключенные между параллельными хордами, равны.

   

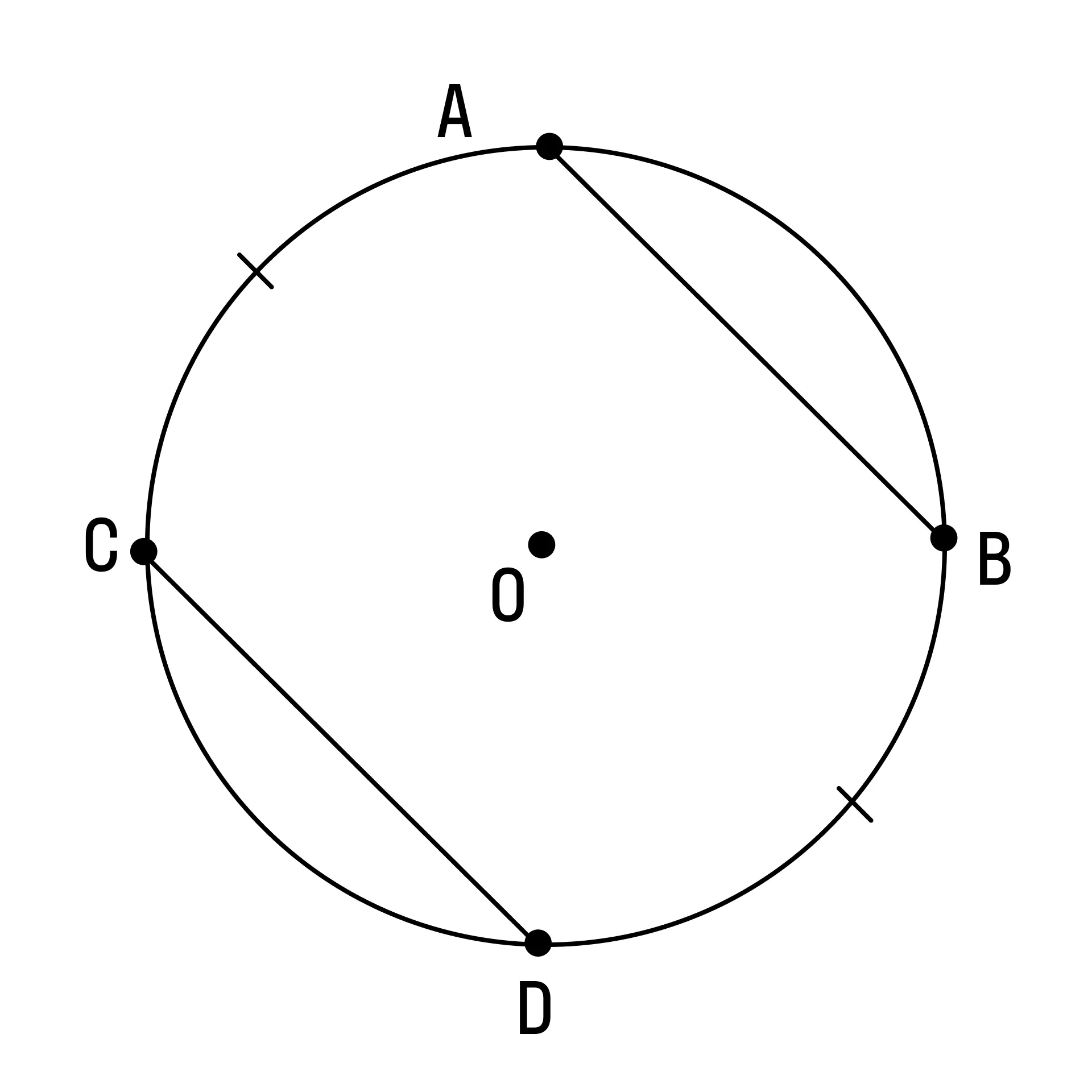
3. В окружности равные хорды равноудалены от центра окружности.

4. Если две хорды окружности AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM ⋅ MB = CM ⋅ MD.

   

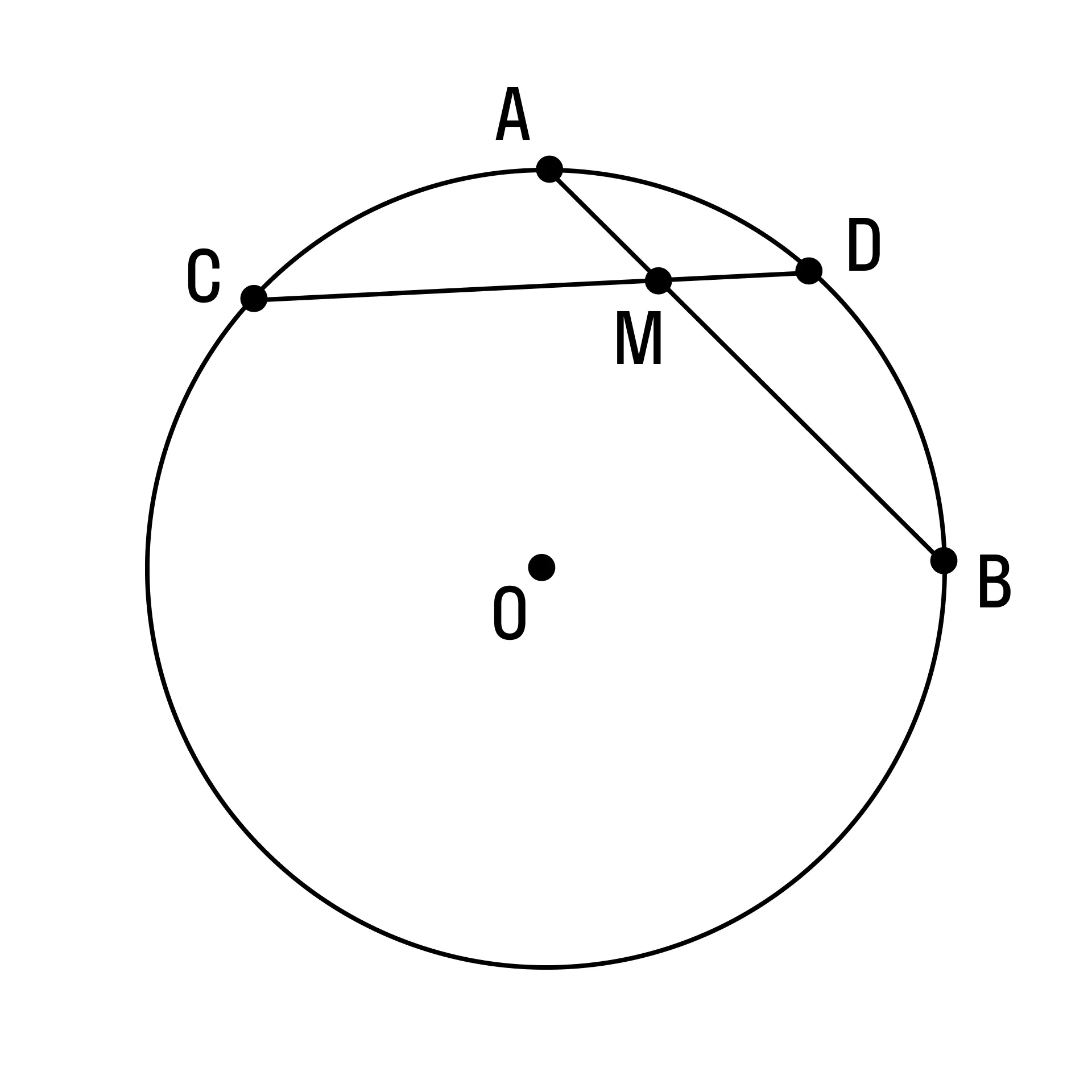
5. Угол между пересекающимися хордами окружности равен половине суммы дуг, заключенных между ними.

Дуга, длина дуги, градусная мера дуги

Дуга — часть окружности, кривая, ограниченная двумя произвольными точками.

Дуга окружности обозначается символом ◡, например ◡АВ, ◡CD.

Любые две различные точки A и B окружности разбивают её на две части; каждая из этих частей называется дугой.

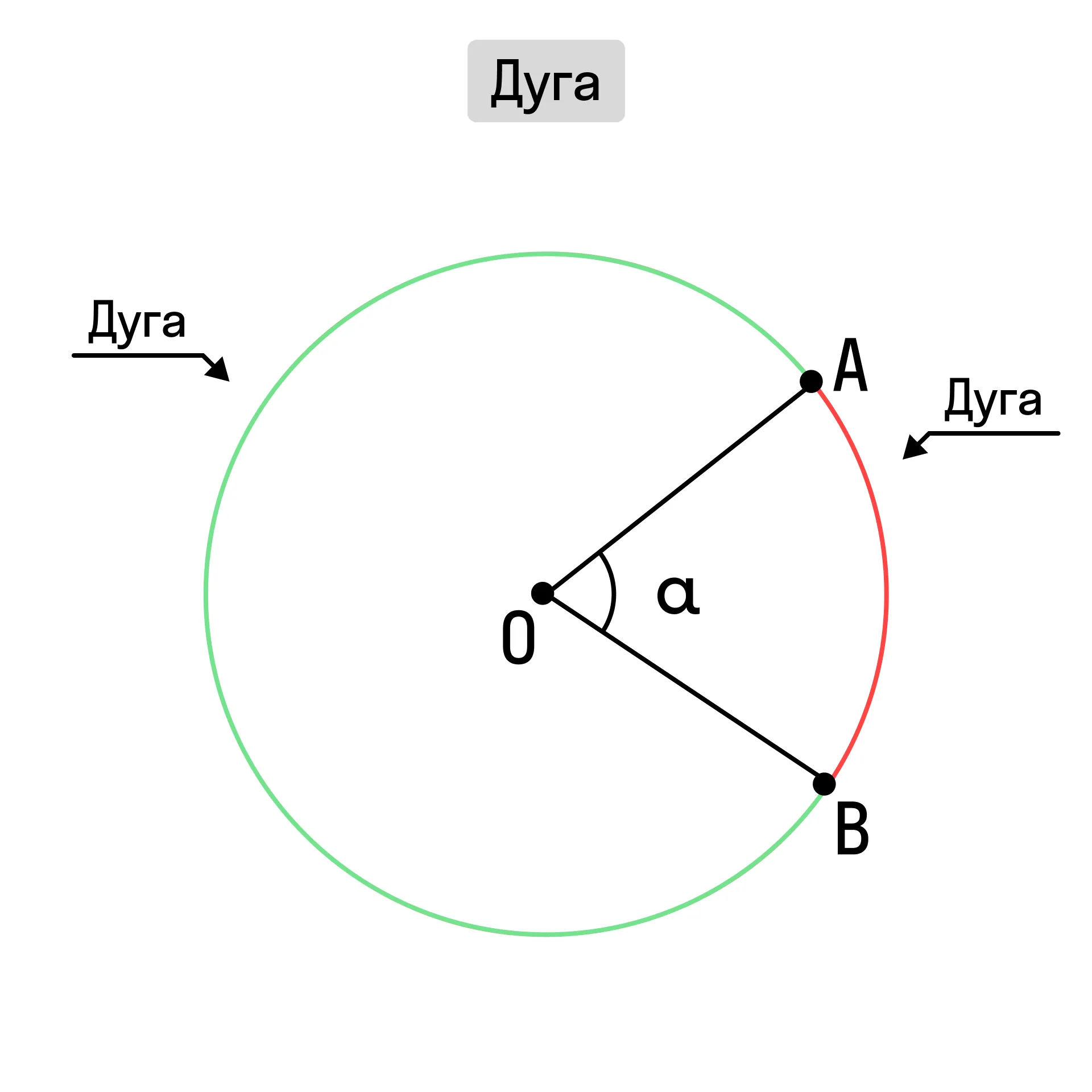
Для дуги есть два измерения: её градусная мера и длина кривой линии, рисующая дугу.

Длину дуги можно рассчитать по формуле:

, где R — радиус окружности, α — центральный угол, стягивающий дугу.

Градусная мера дуги равна центральному углу, на который она опирается.

Т. е. если угол α равен 60°, то и малая дуга АВ также равна 60°.

Вы уже заметили, что дуга связана с центральным углом, но что это? Давайте узнаем!

Центральный угол, вписанный угол и их свойства

Центральный угол окружности — угол, вершина которого совпадает с центром окружности.

Вписанный угол окружности — угол, вершина которого лежит на окружности.

348.5K

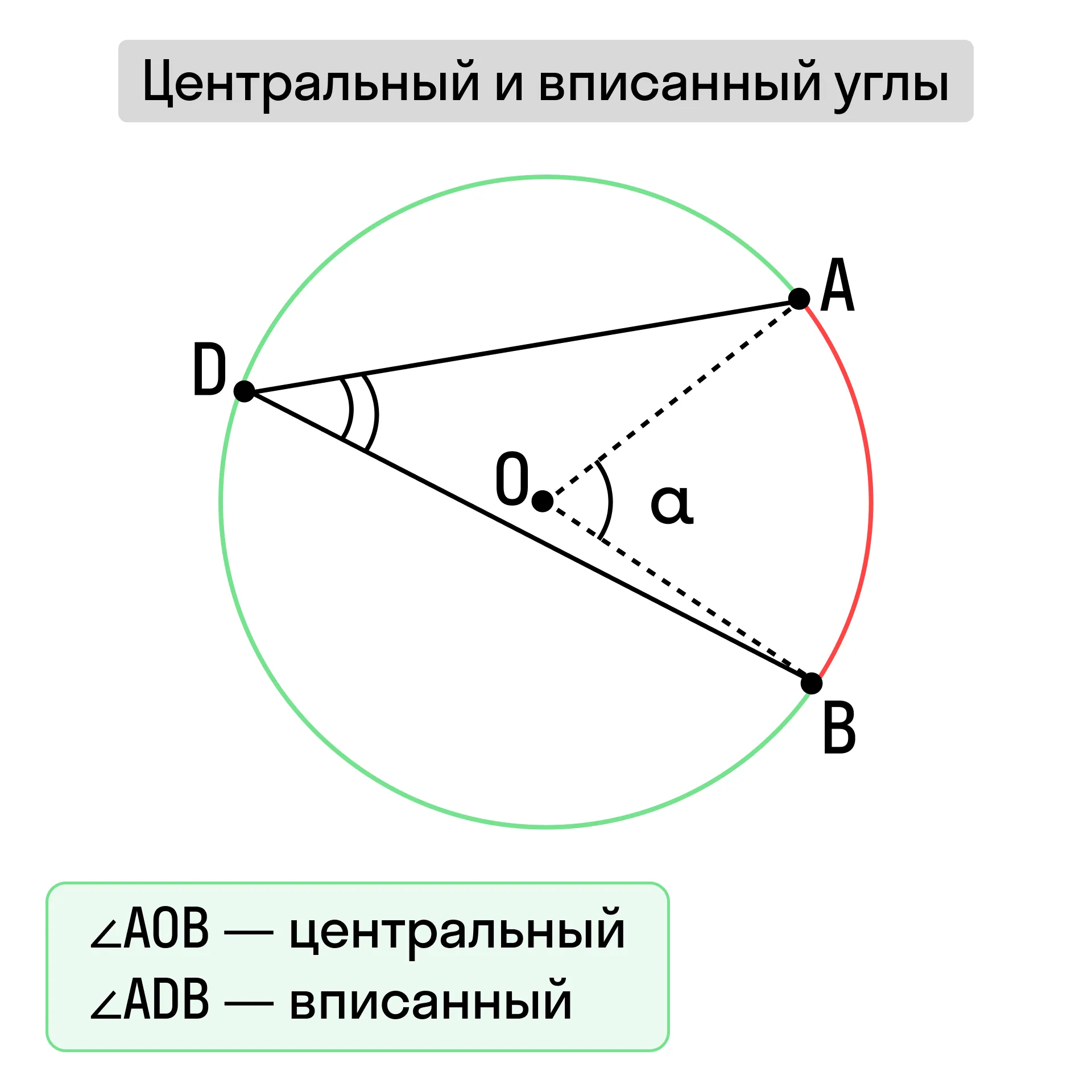
Центральные и вписанные углыЧитать →

Между центральным и вписанным углом, стоящих на одной дуге, есть следующее соотношение — вписанный угол равен половине центрального угла, опирающегося на ту же дугу: ∠ADB = ½∠AОB.

Какие ещё свойства важно знать для решения задач?

1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.

   

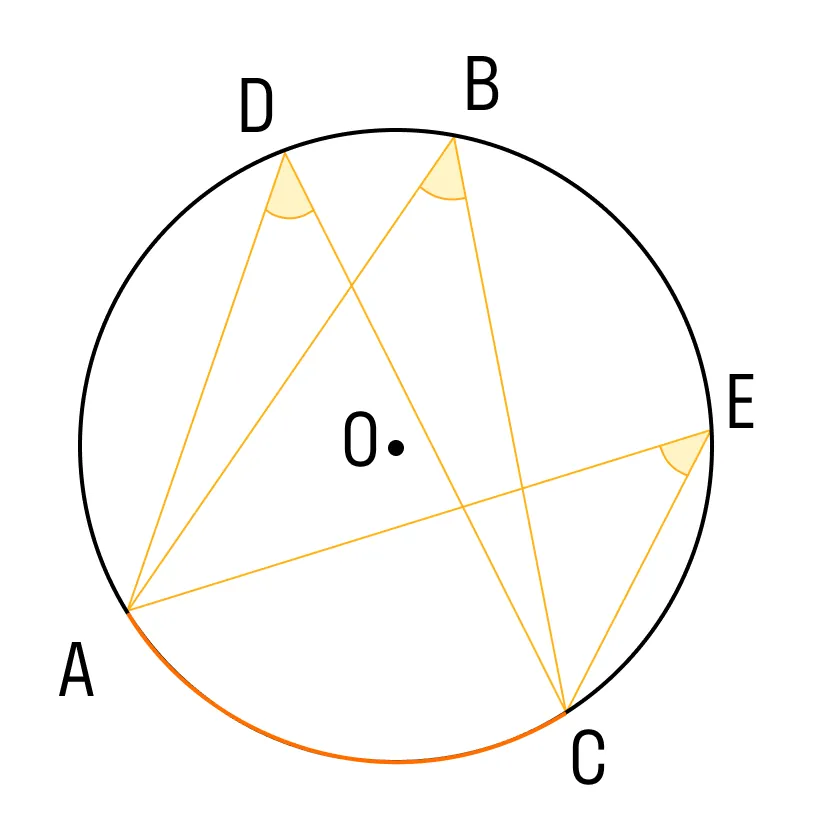
   ∠ADС = ∠ABС = ∠AEС

2. Если вписанный угол опирается на диаметр окружности, то такой угол — прямой.

   

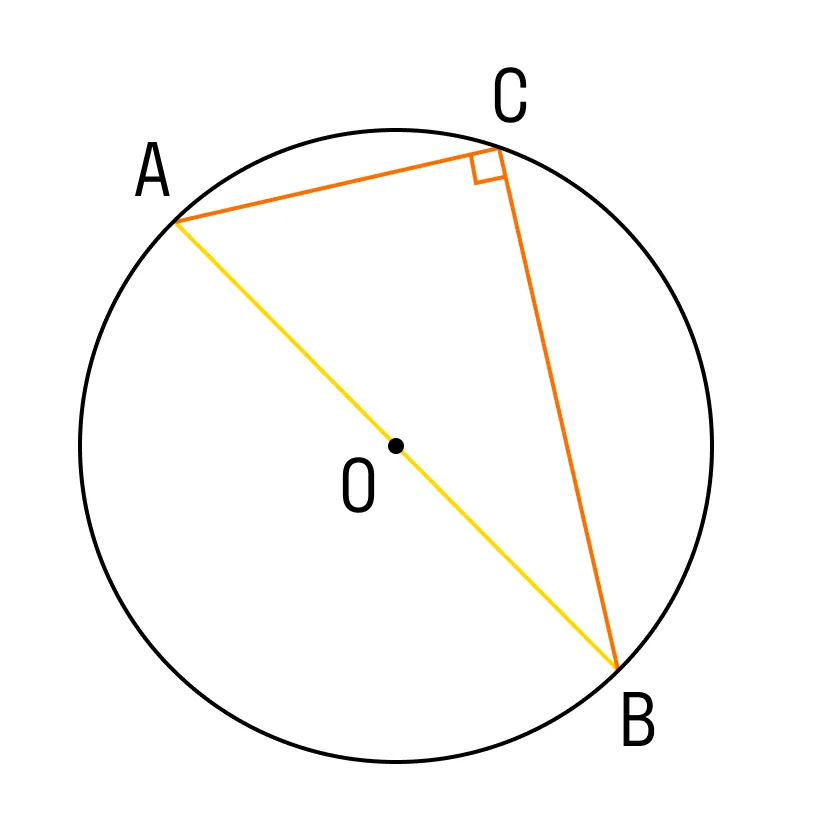
Чем можно объяснить это свойство? Диаметр отсекает половину окружности, градусная мера этой дуги равна 180°. Тогда вписанный угол, который на неё опирается, будет равен половине дуги. т. е. 90°.

Касательная и секущая окружности

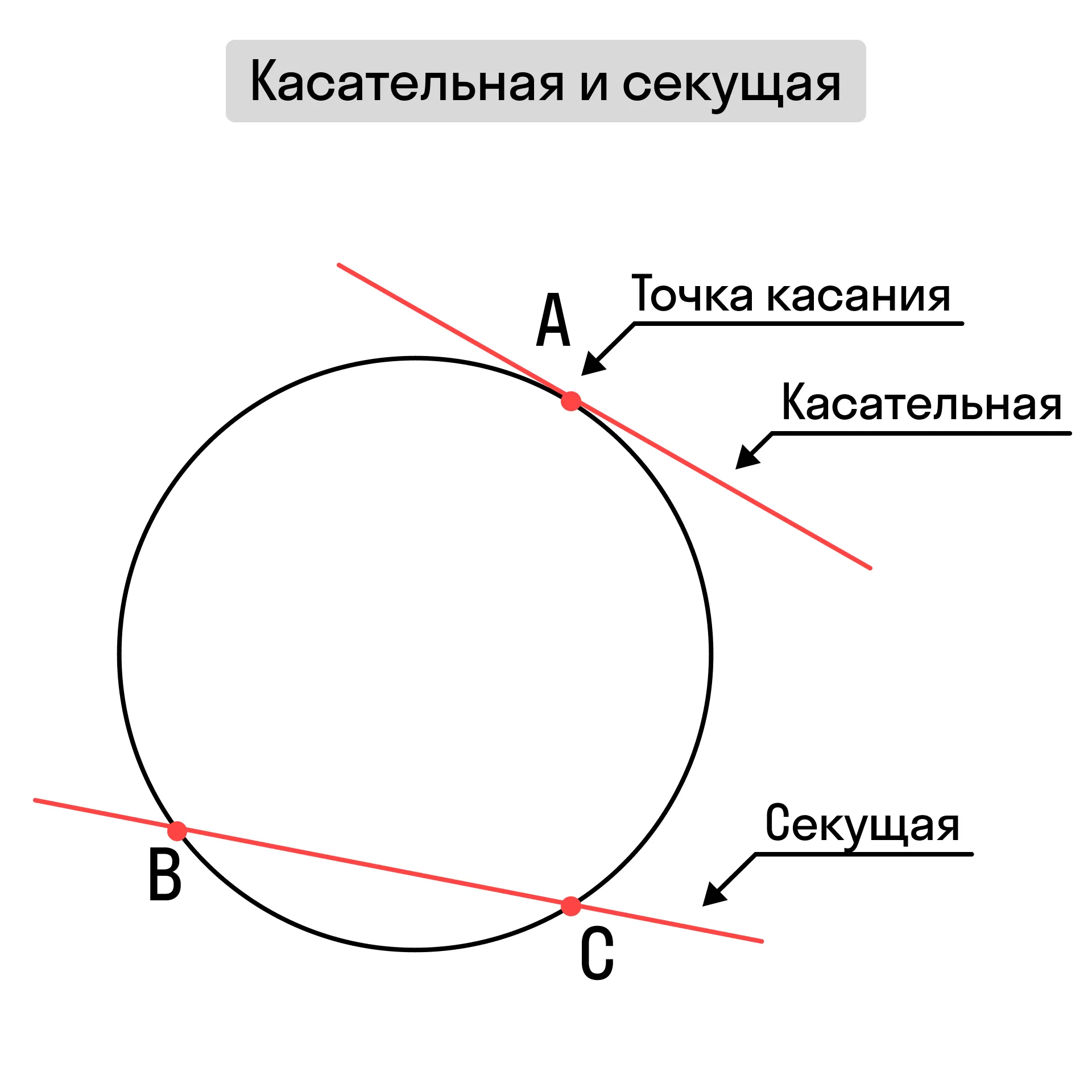
Касательная к окружности — прямая, которая имеет с окружностью только одну общую точку.

Секущая окружности — прямая, пересекающая окружность в двух точках.

Свойства касательных

1. Касательная к окружности перпендикулярна радиусу, проведённому к точке касания.

2. Отрезки касательных, проведённых из одной точки к окружности, равны. Эти отрезки составляют равные углы с прямой, проходящей через эту точку и центр окружности.

   

323K

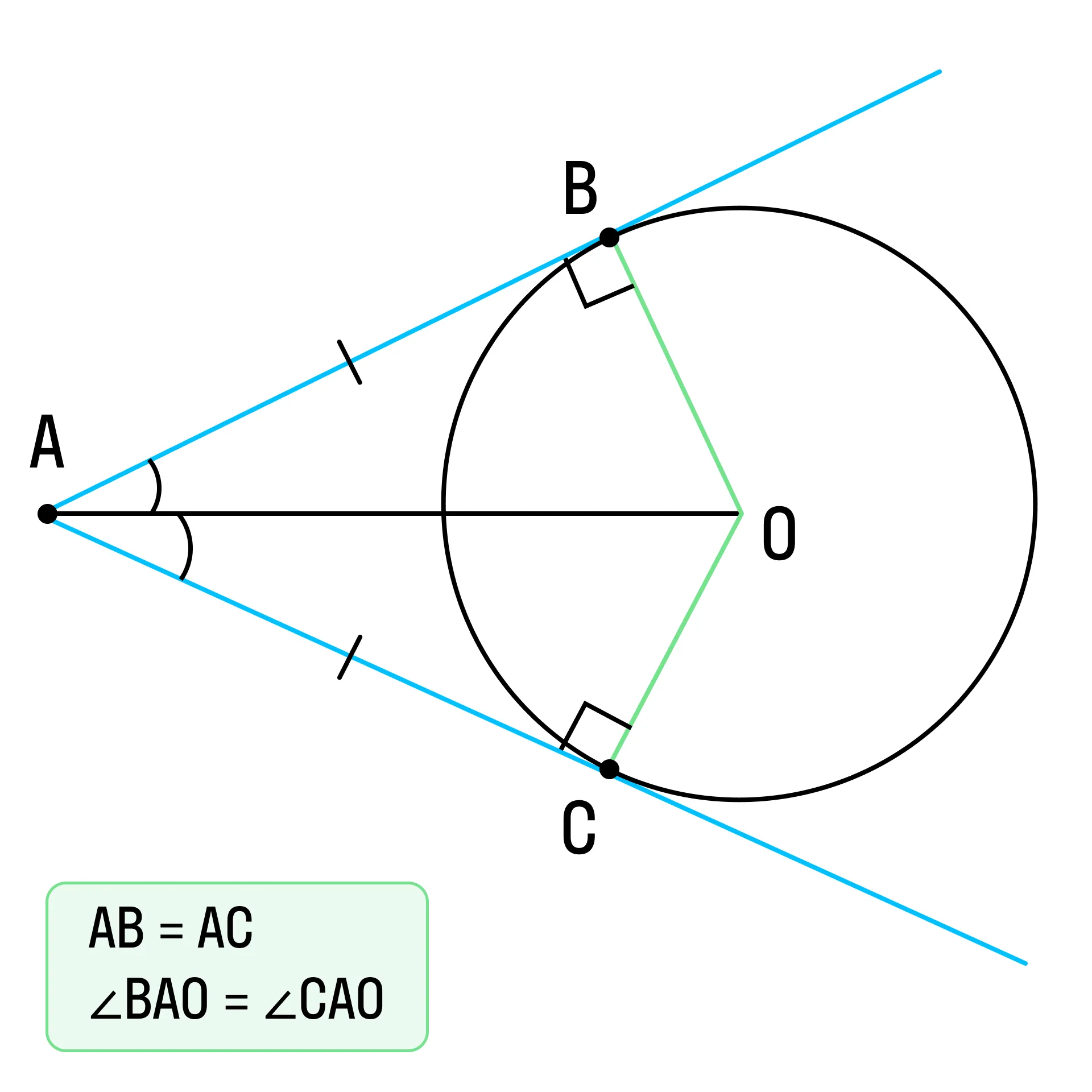
Касательная к окружностиЧитать →

Теоремы о секущей и касательных

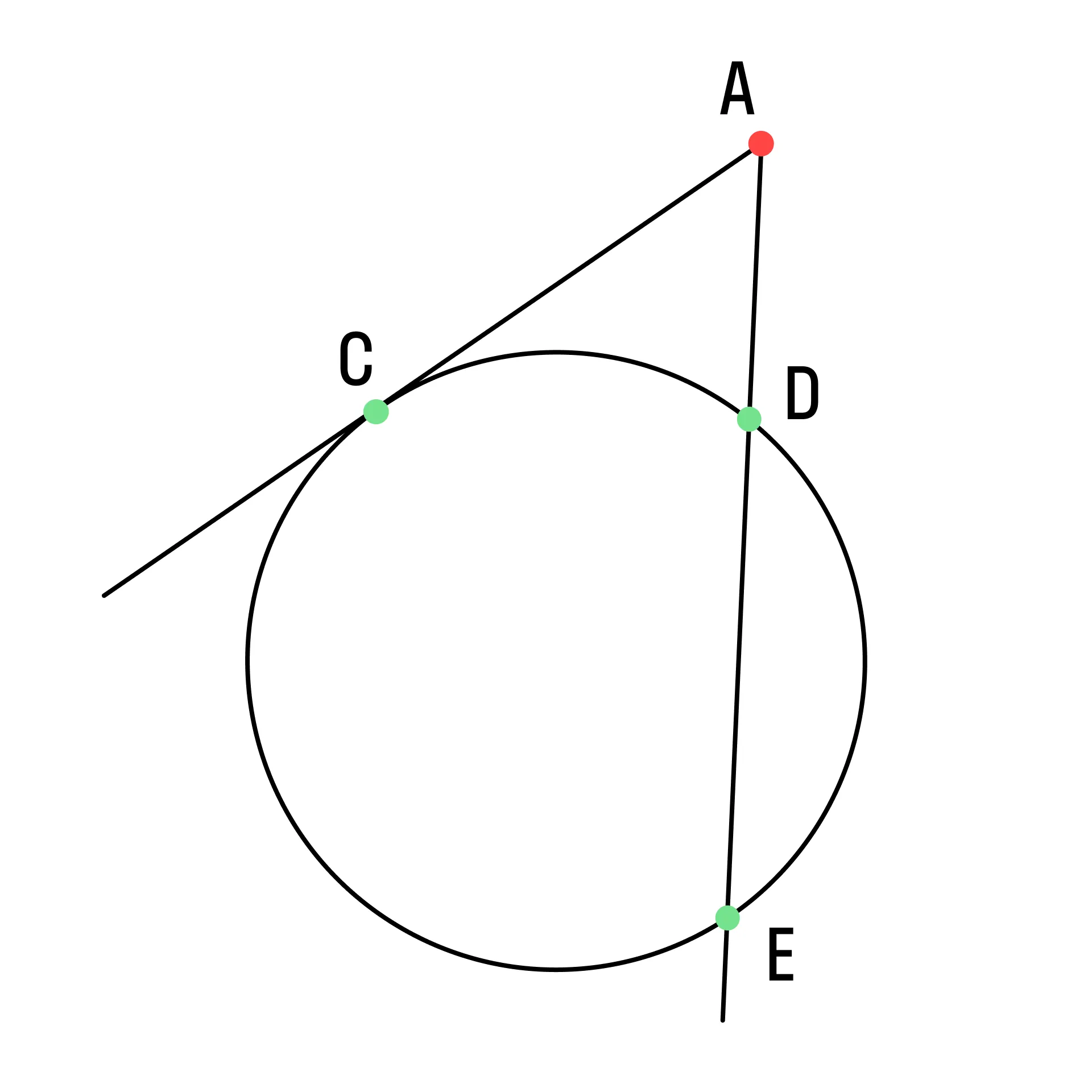
1. Для любых секущей и касательной, проходящих через точку А, верно равенство:

   AC² = AD ⋅ AE

   

2. Для любых двух секущих, проходящих через некоторую точку O, выполняется равенство:

   

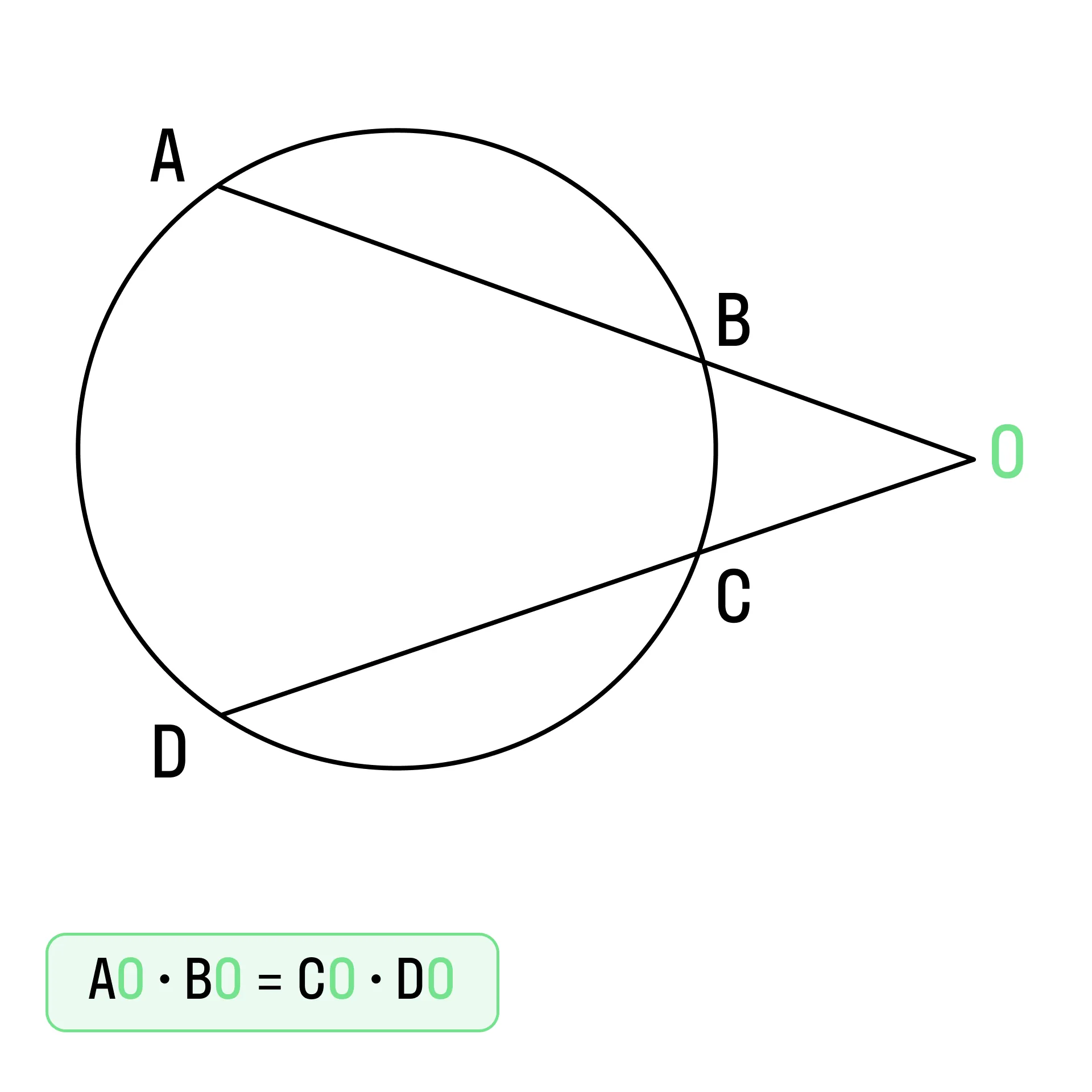
Углы и дуги между касательными и секущими

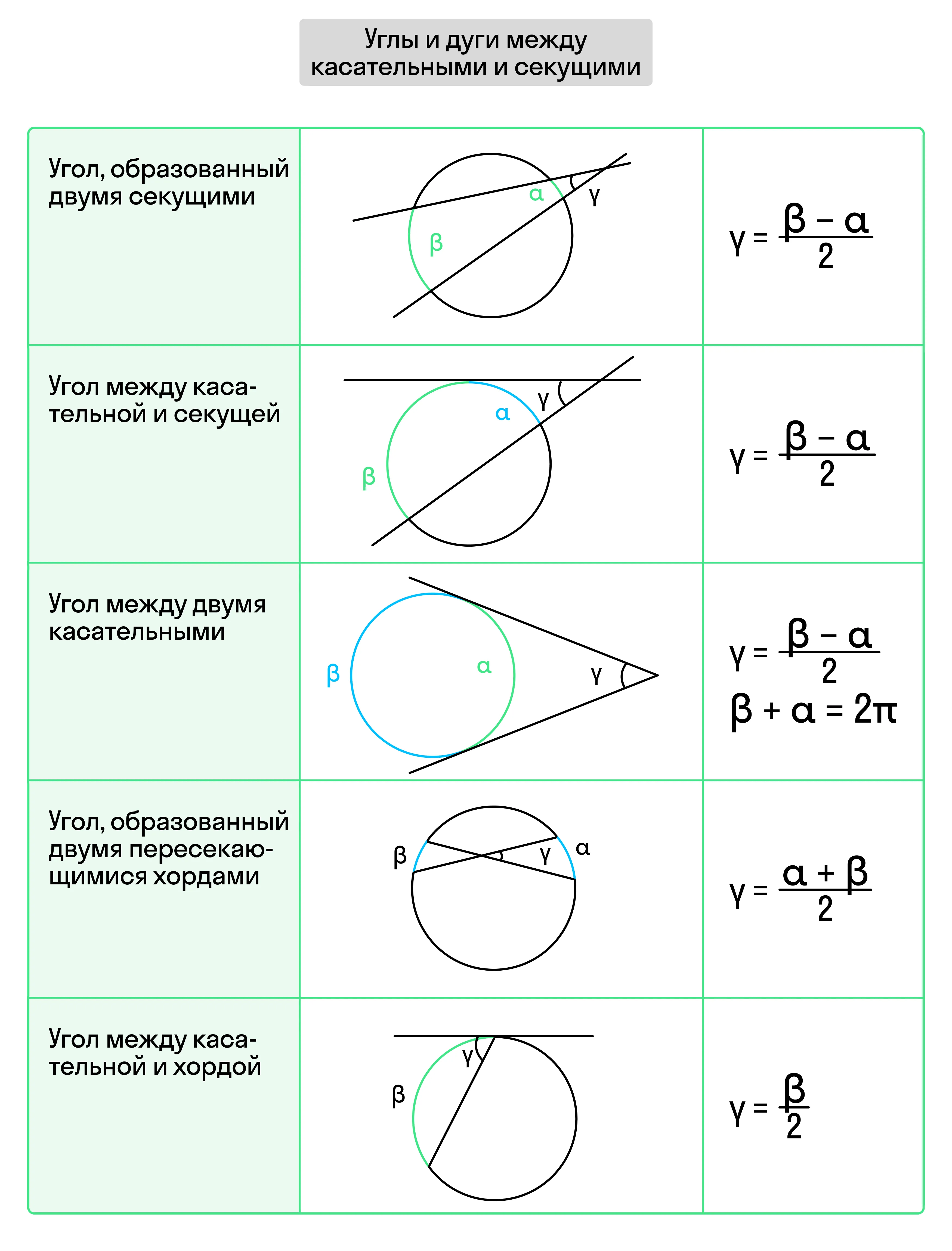
Между дугами и углами, образованными секущими и касательными, соблюдаются следующие соотношения. Сохраняйте памятку себе и отправляйте друзьям!

Основные свойства окружности

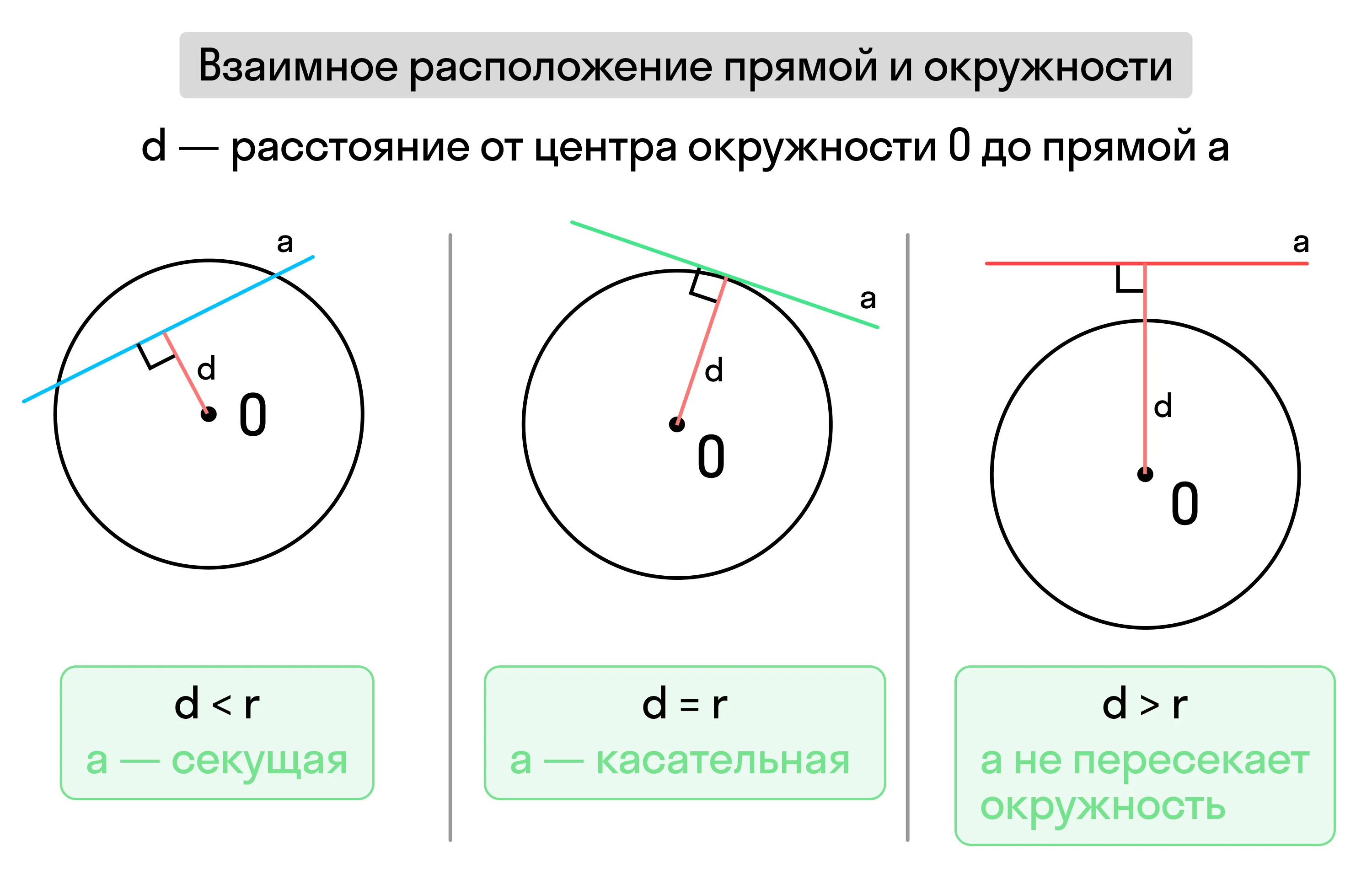
1. Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).

   

2. Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.

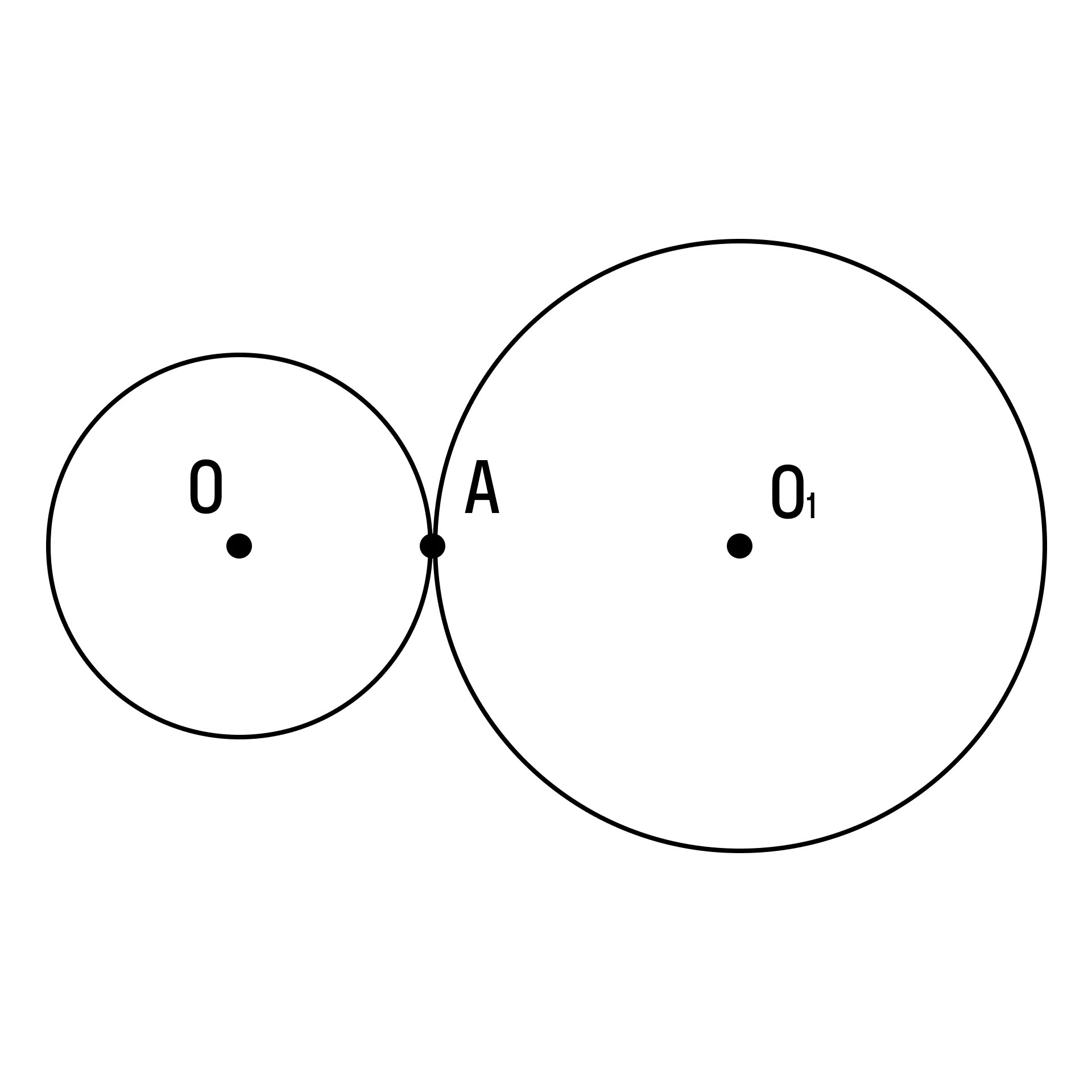
3. Точка касания двух окружностей лежит на линии, соединяющей их центры.

   

4. Градусная мера окружности равна 360°.

Формулы длины окружности и площади круга

Длина окружности — аналог периметра: если в многоугольнике периметр равен сумме всех сторон, то длина окружности — это длина кривой (т. к. в окружности нет сторон, было бы неверным применять для нее понятие периметра).

Длина окружности чаще всего обозначается буквами l или С.

C = 2πR = πD, где

• π ≈ 3,14 — математическая константа (постоянная величина);

• R — радиус окружности;

• D — диаметр окружности.

694.5K

Длина окружности. Онлайн-калькулятор длины окружностиЧитать →

Откуда взялось число π (пи)?

Давайте ещё раз рассмотрим формулу для длины окружности и выразим из неё это число:

То есть число π показывает отношение длины окружности к её диаметру. Ещё в древние времена учёные заметили, что это отношение (частное, разница) соблюдается в любой окружности, какой бы большой или маленькой она ни была.

Число π — бесконечная десятичная дробь, но для удобства её округляют до значения 3,14. То есть диаметр окружности меньше длины окружности чуть более чем в три раза.

Площадь круга можно вычислить по формуле

, где

• R — радиус круга;

• D — диаметр круга.

735.5K

Площадь круга: как найти, формулы и калькуляторЧитать →

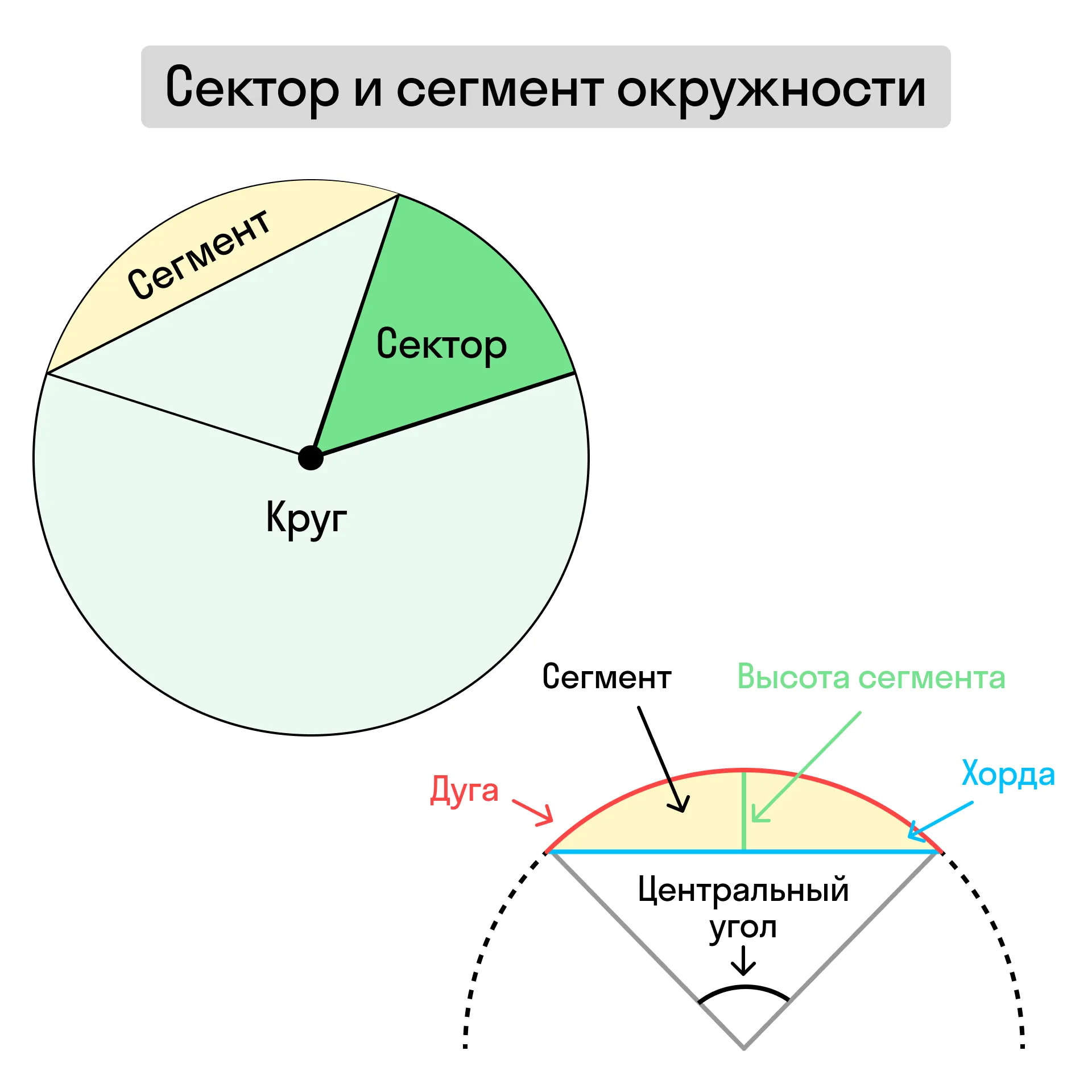
Сектор и сегмент окружности, их площади

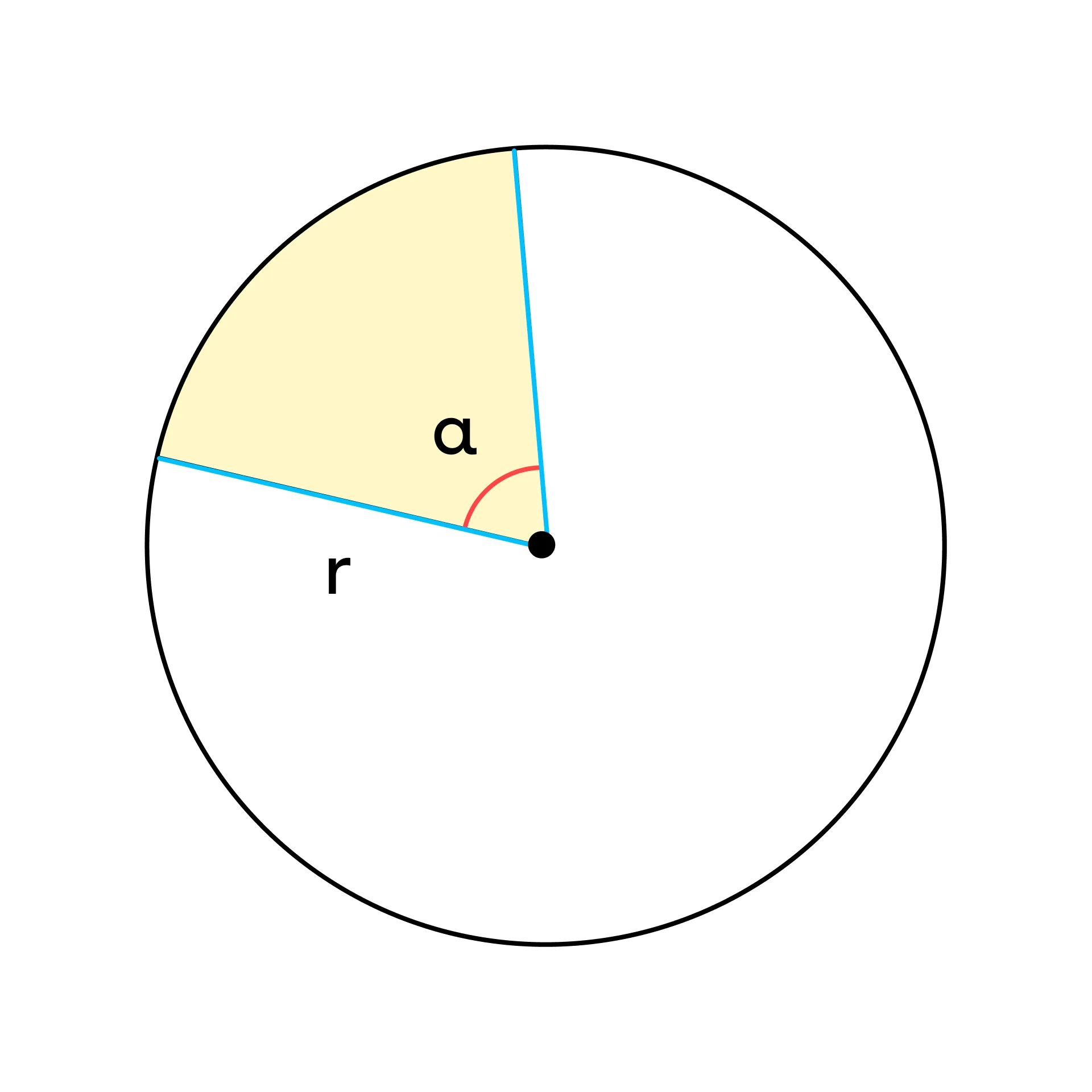
Сегмент — часть круга, ограниченная хордой и дугой.

Сектор — часть круга, ограниченная двумя радиусами и дугой.

	Площадь сектора можно найти по формуле: , где α — угол сектора; R — радиус окружности.
	Формула для вычисления площади сегмента: , где α — угол сегмента; R — радиус окружности.

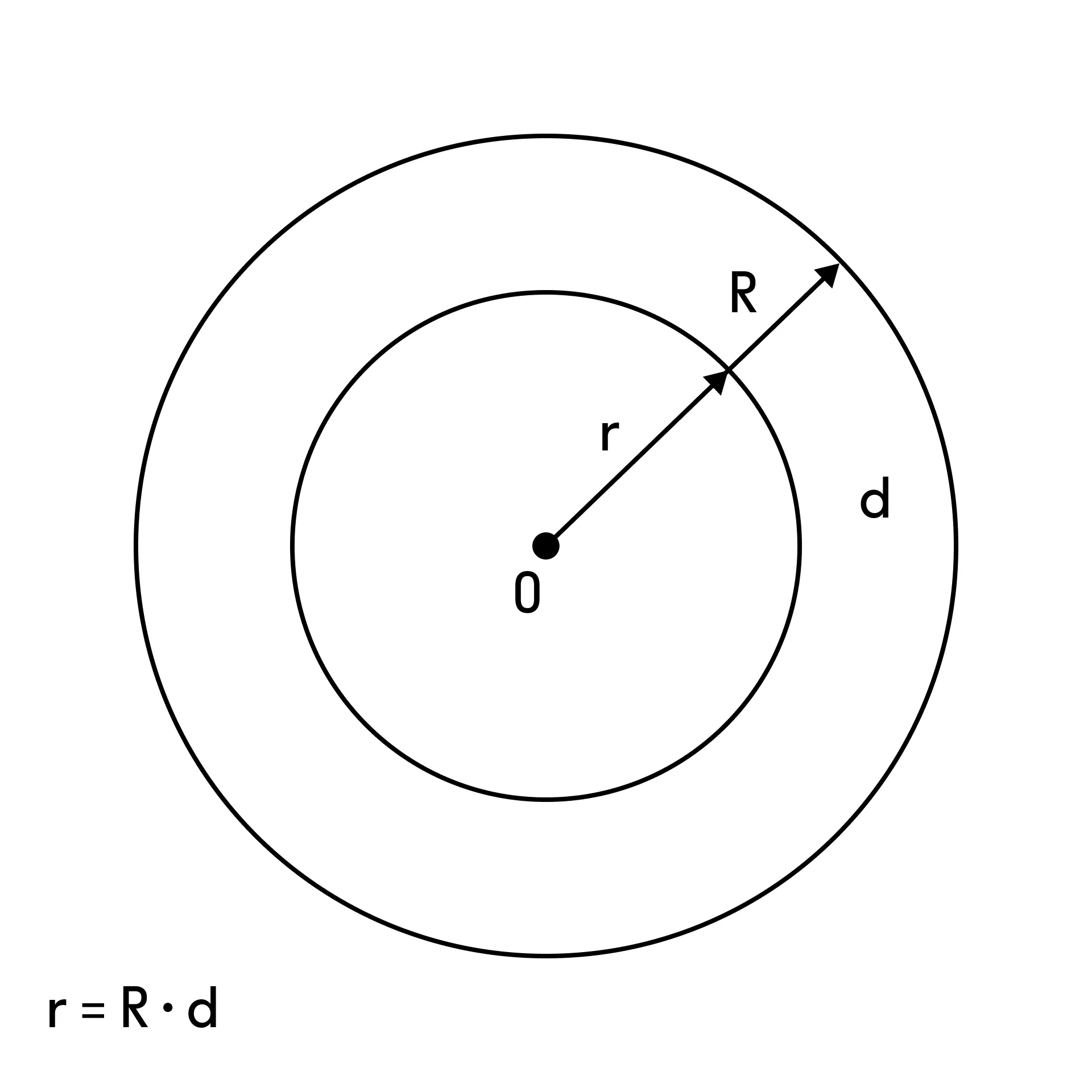
Концентрические окружности и кольцо

Концентрические окружности — окружности с различными радиусами, имеющие общий центр.

Кольцо — часть плоскости, ограниченная двумя концентрическими окружностями.

Уравнение окружности

Окружность, как кривую, можно задать с помощью уравнения.

Так, окружность с центром в точке О, совпадающей с началом координат в декартовой системе, задаётся уравнением:

x² + y² = r², где r — радиус окружности.

Если центр окружности задан точкой с координатами (a; b), уравнение окружности выглядит так:

(x − a)² + (y − b)² = r²

Например, уравнение окружности с центром в точке (−2; 3) и радиусом, равным 5, выглядит так:

(x + 2)² + (y − 3)² = 25 или x² + 4x + y² − 6y − 12 = 0

Хотите закрепить новые знания на практике? Переходите в бесплатный тренажёр ЕГЭ от Skysmart и решайте типовые задачи на окружность по геометрии. Так вы не только повторите пройденную тему, но и сможете подготовиться к контрольным работам и экзаменам!