Формула середины отрезка на плоскости - это способ нахождения координат точки, которая находится ровно посередине между двумя данными точками. Для концов отрезка A xₐ, yₐ и B
Пример: для точек A(2, 3) и B(4, 7) середина будет C(3, 5).
Как найти координаты середины отрезка на координатной прямой
Изобразим горизонтальную координатную прямую оХ и отметим на ней две точки: М и L. Координату точки М запишем как Хм, точки L — соответственно XL. Поставим лежащую на отрезке точку А — середину ML, MA = LA.
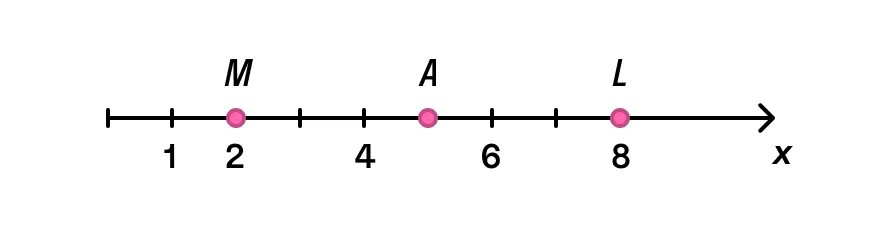
Определим координаты точек: Хм = {2}, XL = {8}. Чтобы найти середину отрезка, воспользуемся формулой XA=(XM+XL)/2 и получим:
Проверим, верна ли формула. Для этого определим координаты середины отрезка графическим методом.Действительно: фактическая координата точки А совпадает со значением, которое мы получили.
Подумайте, взяли ли мы эту формулу случайно или же ее можно вывести. Да, конечно, второй вариант верный — в математике не используют ничего непроверенного. Давайте посмотрим, каким образом можно доказать истинность формулы, тем более, что мы возьмем ее за основу при решении более сложных задач.
Точка А — это середина отрезка, а значит, MA = LA.
Расстояние между точками можно рассчитать через разность модулей их координат: │ХА – ХМ│=│ХL – ХА│.
Преобразуем правую часть, вынесем знак минуса: ХА – ХМ= - (ХА –ХL).
Перенесем ХА в левую часть, а все остальное — в правую: 2ХА= ХL+ ХМ.
Найдем ХА: ХА = (ХL + ХМ)/2.
Вот мы и вывели формулу координат середины отрезков! Чтобы лучше закрепить материал, сделаем пару заданий.
Задача 1
Определите координаты середины отрезка АВ, если ХА = –2, ХB = 10.
Решение
Обозначим точку середины отрезка буквой Т. Тогда Хт = (ХА + ХB)/2 = (–2 + 10)/2 = 4.
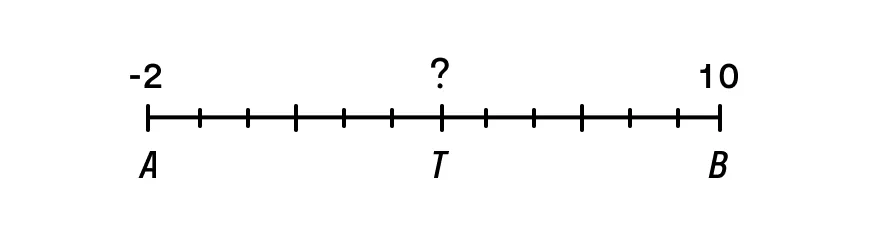
Ответ: Хк = {4}.
Задача 2
Определите координаты начала отрезка КМ с серединой в точке Н, если Хм = 5, Хн = 10.
Решение
Вначале запишем формулу для середины отрезка: Хн = (Хк + Хм)/2. Выразим Хк через нее:
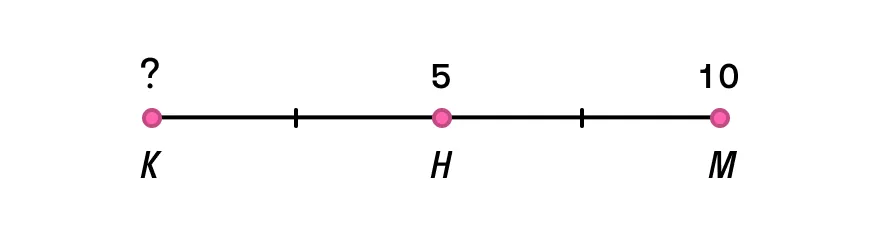
Ответ: Хк = {0}
Как найти середину отрезка на плоскости
В Декартовой системе координат у каждой точки есть две координаты: по оси оХ и оУ. Изобразим отрезок АВ с координатами А (1; 3), В (3; 6) и точкой С — серединой отрезка.
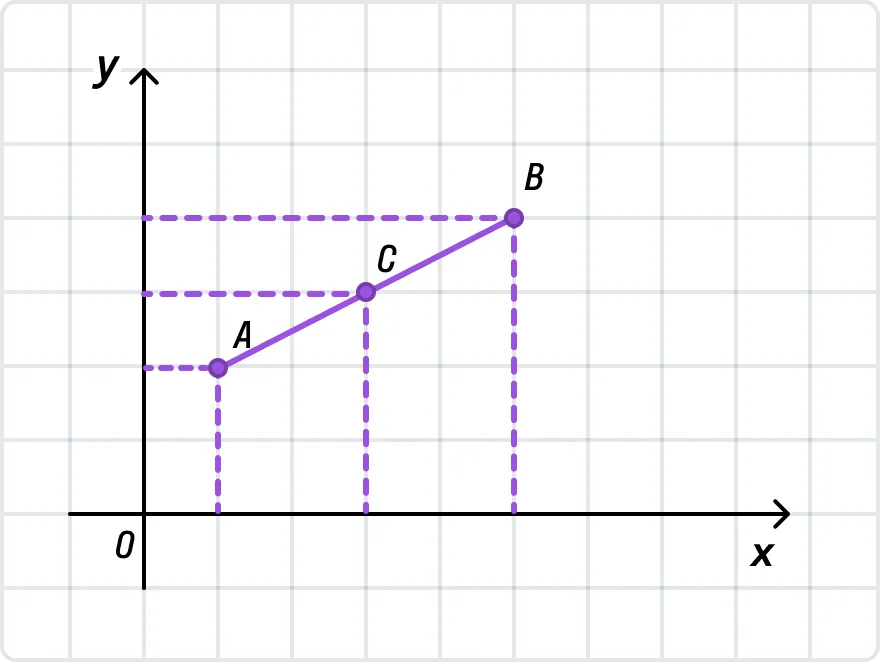
Чтобы найти координаты точки С, мы воспользуемся уже известной нам формулой, но применим ее к каждой координате в отдельности. Вначале рассчитаем Хс:
Тогда УC = (УA + УB)/2 = (3 + 6)/2 = 4,5. Значит С (2; 4,5).
Не пугайтесь, если отрезок на чертеже параллелен оси оХ или оУ: мы четко идем по нашему алгоритму и ничего не меняем.
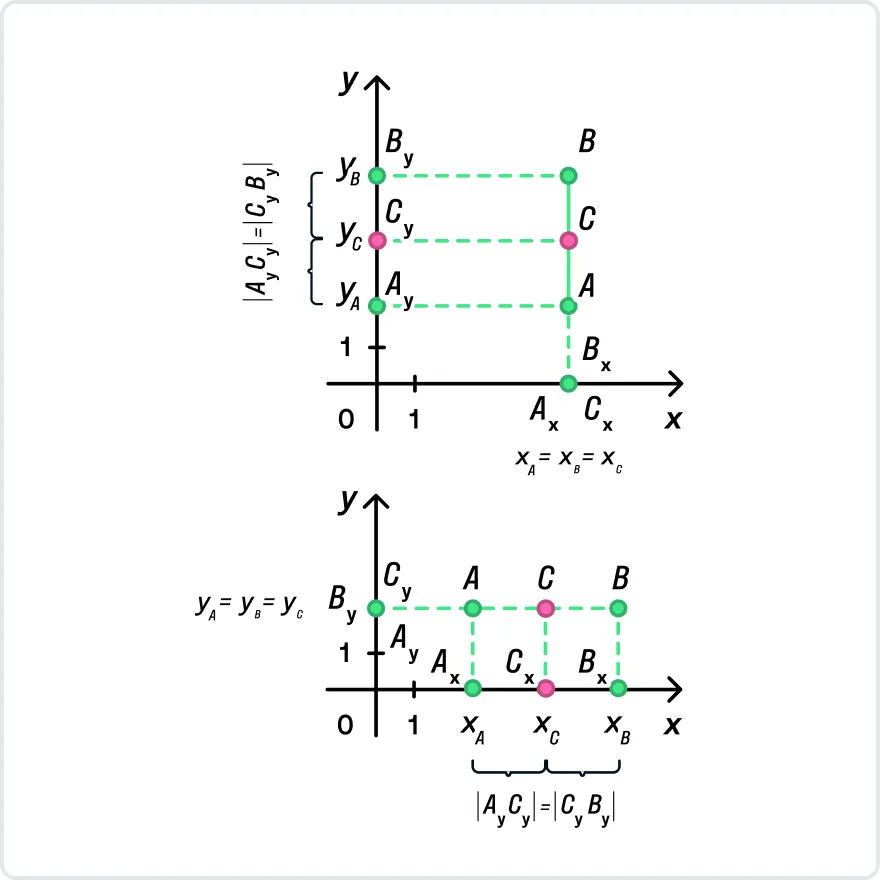
Важно заметить: если отрезок параллелен оси оУ, координаты концов и середины отрезка по оХ будут совпадать, ХА = ХС = ХВ. Если же отрезок параллелен оси оХ, совпадут координаты по оУ: УА = УВ = УС.
И вновь пришло время задачек. Давайте разберем несколько примеров решения.
Задача 3
В системе координат находятся две точки: С (–6; 4) и К (2; 8). Определите координаты середины отрезка.
Решение
Обозначим середину отрезка точкой О. Тогда:
Ответ: О (-2; 6).
Задача 4
Дан треугольник с вершинами АВС: А (-2; 4), В (4; 6), С (3; -5). Определите координаты точки М — медианы ВМ.
Решение
Медиана — отрезок, который проведен из вершины треугольника и делит противоположную сторону пополам. А значит, медиана ВМ делит на равные части сторону АС, АМ = МС. Тогда:
Ответ: М (0,5; –0,5).
Получи больше пользы от Skysmart:
-
Подготовься к ОГЭ на пятёрку.
-
Подготовься к ЕГЭ на высокие баллы.
Записывайся на бесплатные курсы для детей.
Решай задания в бесплатном тренажёре ЕГЭ.
Что такое отрезок
Чтобы изучить эту тему досконально, давайте начнем с самого простого: с определения отрезка.
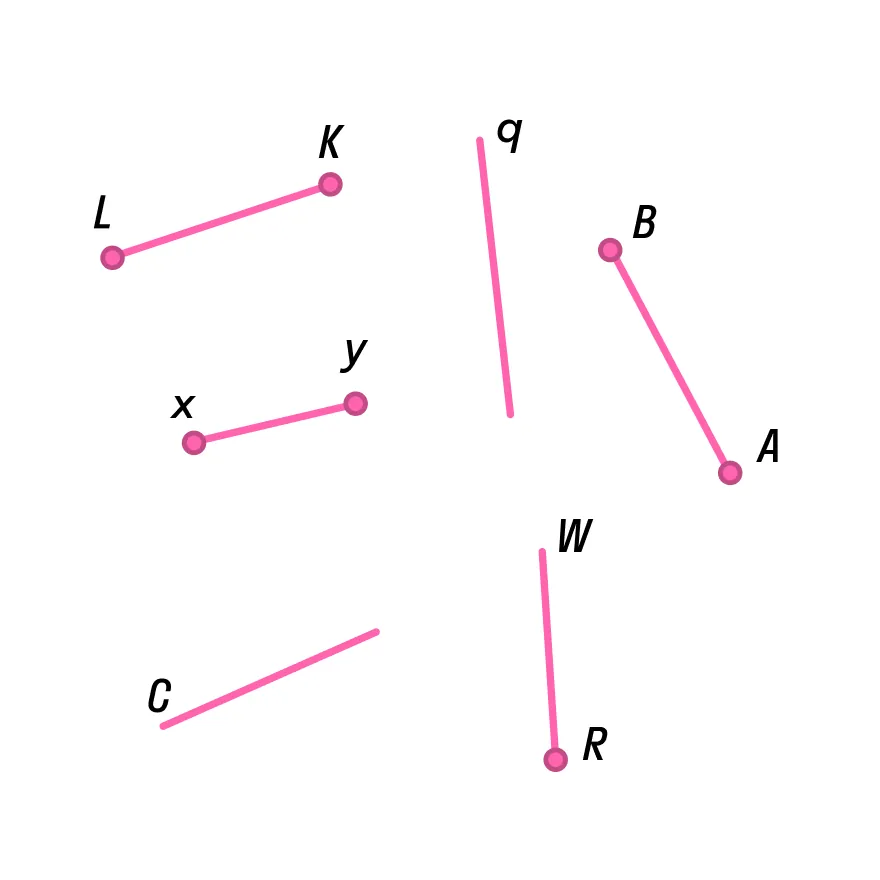
Отрезок называют заглавными буквами латинского алфавита по названию конечных точек. Причем можно расставлять буквы в любом порядке: АВ и ВА — равноценные варианты. Рассмотрите иллюстрацию, посчитайте и назовите все отрезки.
Что такое середина отрезка
Середина отрезка — это точка, находящаяся на равном расстоянии от обоих концов данного отрезка. Если координаты концов отрезка A(x₁, y₁) и B(x₂, y₂), то середина отрезка имеет координаты M((x₁ + x₂)/2, (y₁ + y₂)/2).
Например, для отрезка с концами в точках A(2,3) и B(4,7) середина находится в точке M(3, 5).
Так, на рисунке ниже D — середина отрезка СК, так как СD = DK. Обратите внимание, как на чертеже обозначаются равные по длине отрезки — мы ставим на них равное количество черточек.
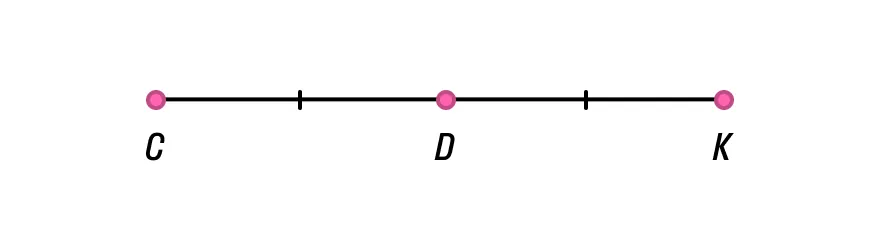
Главный вопрос, который нас сегодня интересует, это координаты середины отрезка.
Мы можем рассмотреть отрезок, который лежит на координатной прямой, тогда координата будет одна. В Декартовой системе координат оХУ будет две координаты, причем вначале записывают х, потом у. Например: С (5; 3): К (4; 8). Еще мы можем поместить отрезок в трехмерное пространство, тогда у каждой точки будет три координаты: х, у, z.
Кажется, что чем дальше, тем сложнее, но на самом деле это не совсем так. Хорошая новость: в каждом из случаев мы будем использовать один и тот же принцип, так что вы обязательно во всем разберетесь!
Координаты середины отрезка в пространстве
Вспомните, чем пространство отличается от плоскости. Правильно, третьим измерением! В том смысле, что добавляется еще одна координатная ось: оZ. Как это выглядит, можно посмотреть на рисунке ниже.
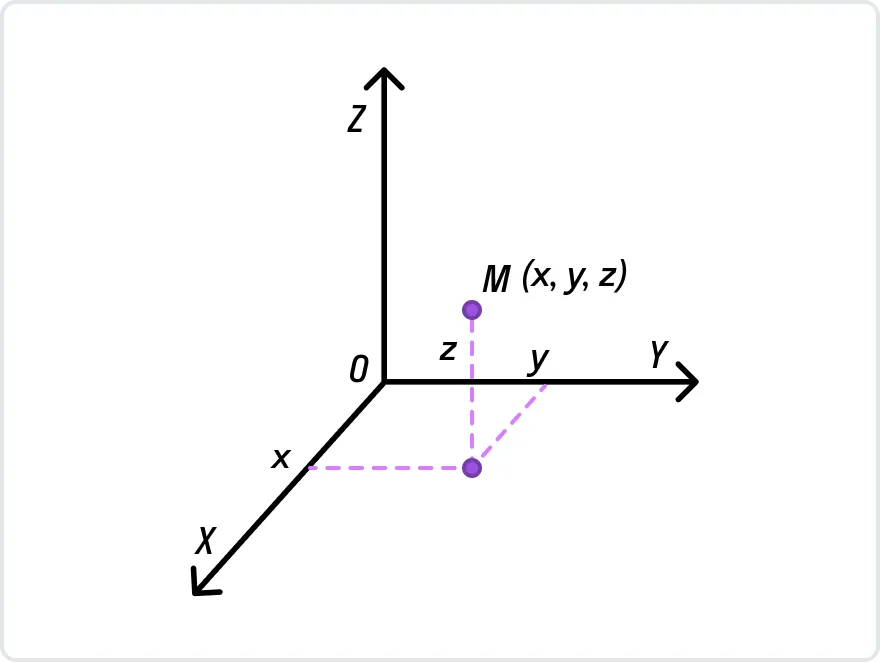
При этом формула нахождения середины отрезка остается неизменной. Если мы изобразим в трехмерном пространстве отрезок АВ с серединой в точке С, тогда:
Координаты середины отрезка через радиус-векторы его концов
По сути, этот способ нельзя назвать каким-то новым и уникальным. Он лишь еще раз доказывает истинность формулы координат середины отрезков, только через алгебру. Чтобы разобраться в нем, давайте сначала вспомним определение вектора.
Векторы — достаточно обширная тема. Чтобы разобраться в ней, не хватит и двух статей. Но сейчас мы с вами будем использовать всего несколько тезисов, которые помогут разобраться в теме.
Векторы можно изображать в системах координат оХУ и оХYZ, т. е. в двумерной и трехмерной.
Координаты начала и конца векторов записывают так же, как и для отрезков: (x; y) и (x; y; z).
Сумму векторов можно найти по методу треугольника или параллелограмма. Картинка ниже поможет вам вспомнить, как ими пользоваться.
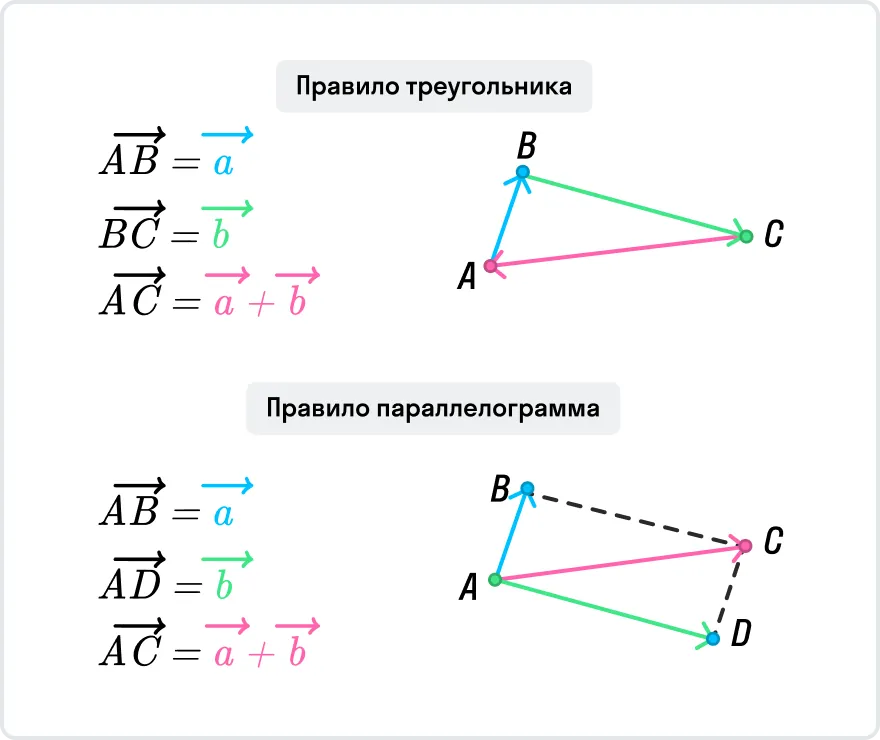
Давайте разберемся, как доказать формулу для нахождения координаты середины отрезка через радиус-векторы его концов. В Декартовой системе координат нарисуем вектор
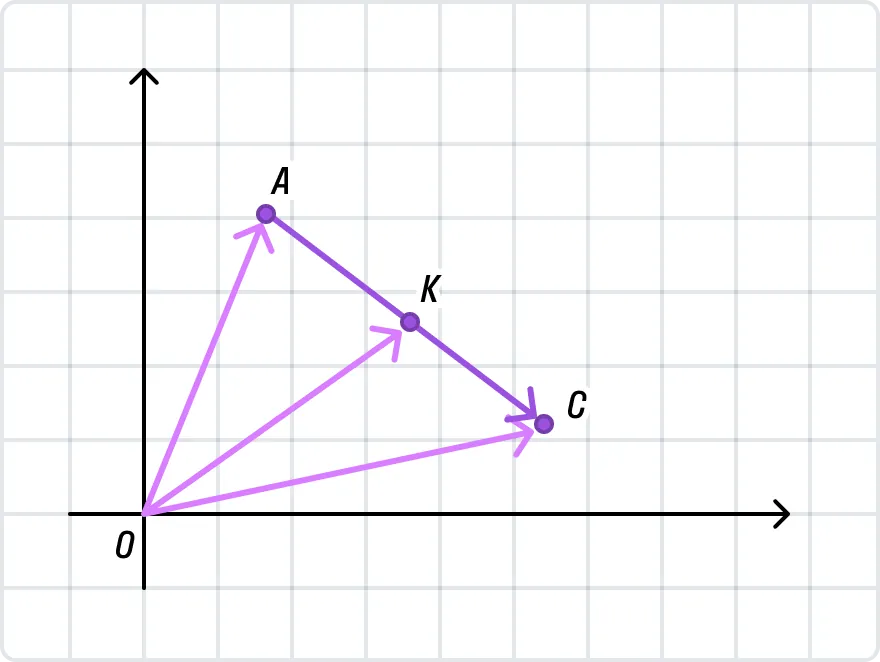
Согласно определению середины отрезка: ОК = ½(ОС + ОА). Координаты векторов ОА, ОК, ОС соответственно равны координатам точек А, К, С, так как координаты точки О (0; 0; 0).
Тогда запишем равенство ОК = ½(ОС + ОА) через координаты:
Напоследок мы сделаем небольшой перерыв, забудем про формулы и числа. Давайте подумаем, как можно найти середину отрезка, если мы не знаем координат его концов.
Например, нарисуем отрезок на песчаном пляже во время каникул. Определить точные координаты в таком случае будет достаточно сложно, правда? Вряд ли вы взяли с собой в отпуск набор линеек, чтобы вычислить длину отрезка. С подобным заданием вы могли столкнуться и на уроках геометрии, где учитель раздавал вам чистые нелинованные листы бумаги и просил найти середину отрезка без использования линейки.
Сейчас мы обучим вас волшебному методу, приготовьтесь! Все что вам понадобится — это циркуль. Нарисуем на бумаге отрезок АВ любой длины. Поставим иголку циркуля в точку А и начертим окружность с радиусом, равным АВ. Далее повторим действие — прочертим такую же окружность с центром в точке В.
Мы видим, что окружности пересеклись дважды: снизу и сверху. Если соединить эти две точки, эта прямая пересечет наш исходный отрезок ровно в его середине.
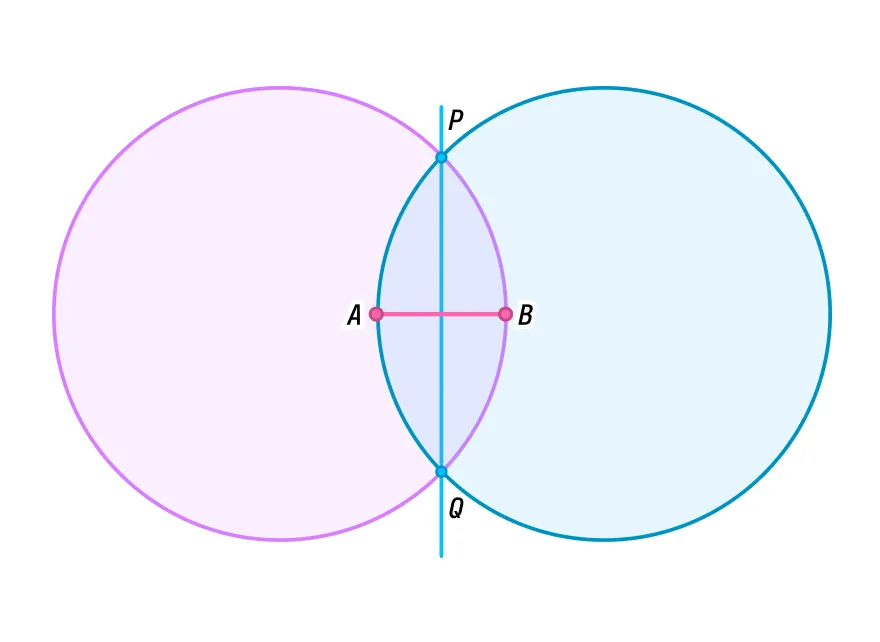
Скептики вспомнят наш пример с пляжем и скажут: «Линейку мы с собой в отпуск не берем, но и циркуль ведь тоже! Что вы скажете на это?» А ответим мы вот что: приходите на курсы по профильной математики в Skysmart! Там вы научитесь не только заменять настоящий циркуль на самодельный, но еще подготовитесь к экзаменам, разовьете логику и узнаете много всего интересного. Ждем вас на занятиях!
