Скалярное произведение векторов — это число, равное произведению их модулей на косинус угла между ними. Обозначается как
Пример:
- Если
Для кого эта статья:
- Студенты и школьники, изучающие математику и физику
- Преподаватели и научные работники в области математики
- Любители и профессионалы, работающие с векторной алгеброй
Основные определения
Система координат — это совокупность определений, позволяющих определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Мы уже рассказывали, как найти координаты точки.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
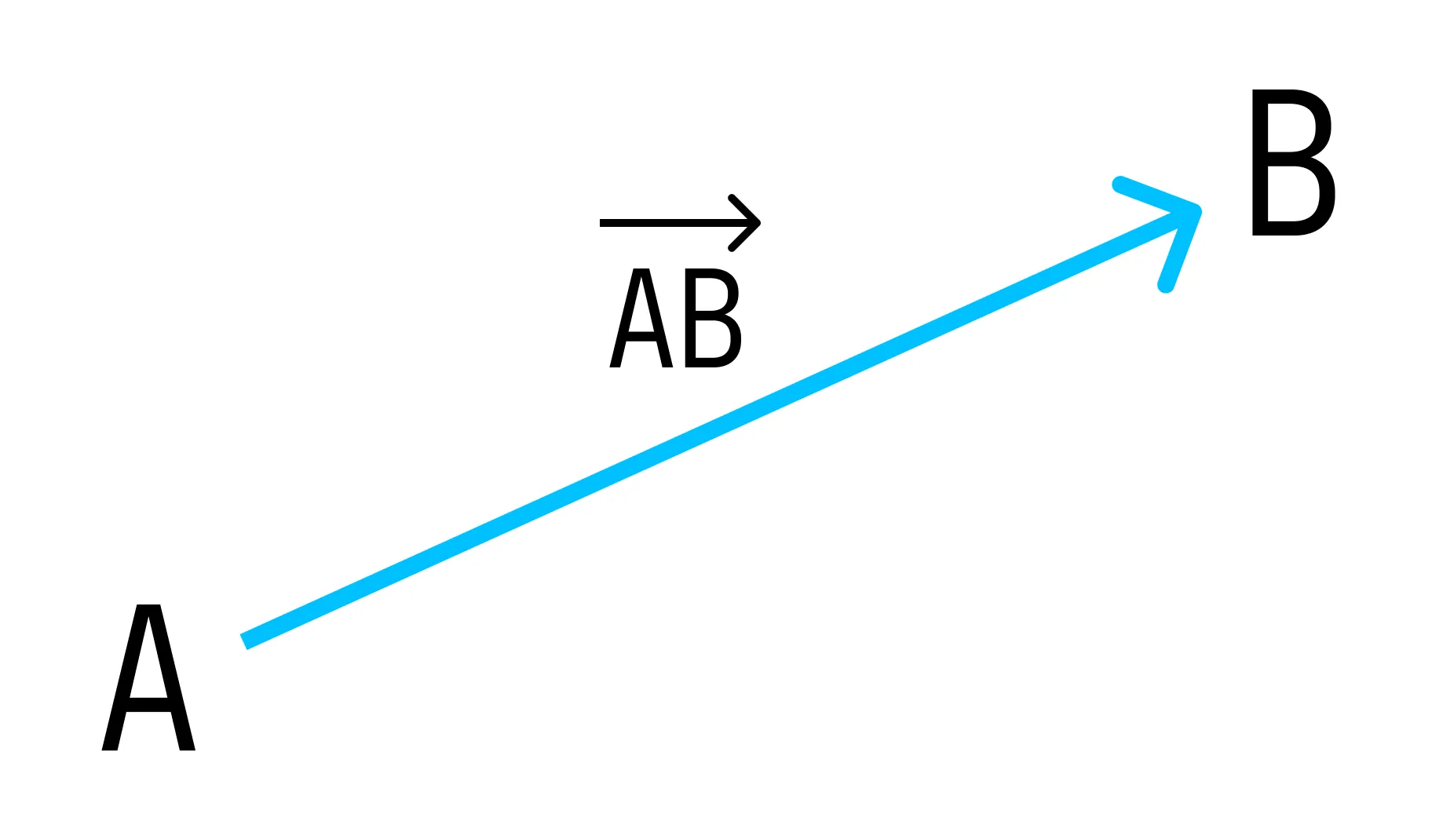
Вектор с началом в точке A и концом в точке B принято обозначать как
Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.
При умножении вектора на вектор получается число. Если длины векторов
Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.

Угол между векторами
Угол между векторами
Значок угла
Пусть даны два вектора
Отложим их от некоторой точки О пространства:
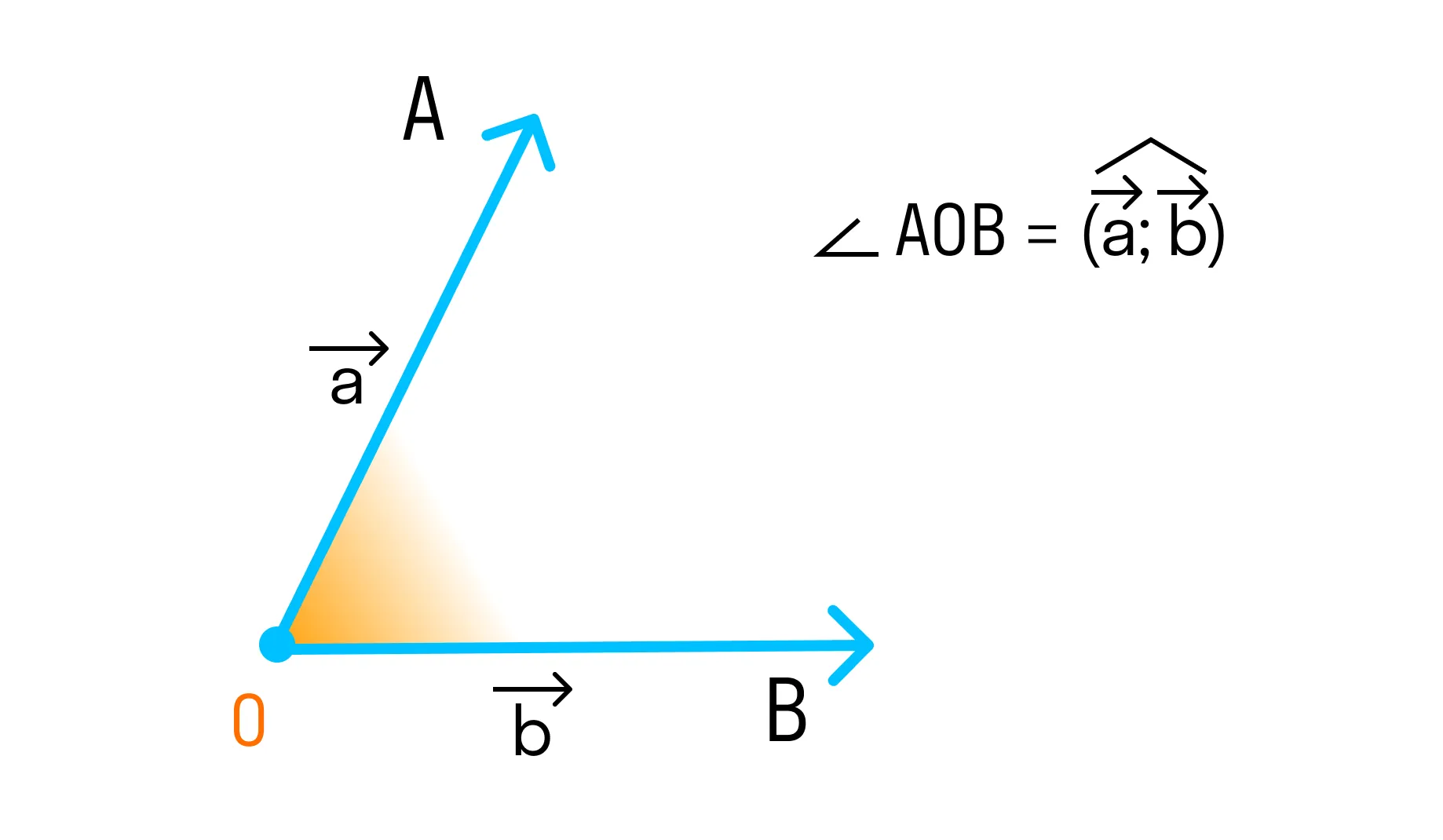
Угол между векторами может быть прямым, тупым, острым или равным нулю. Рассмотрим каждый случай:
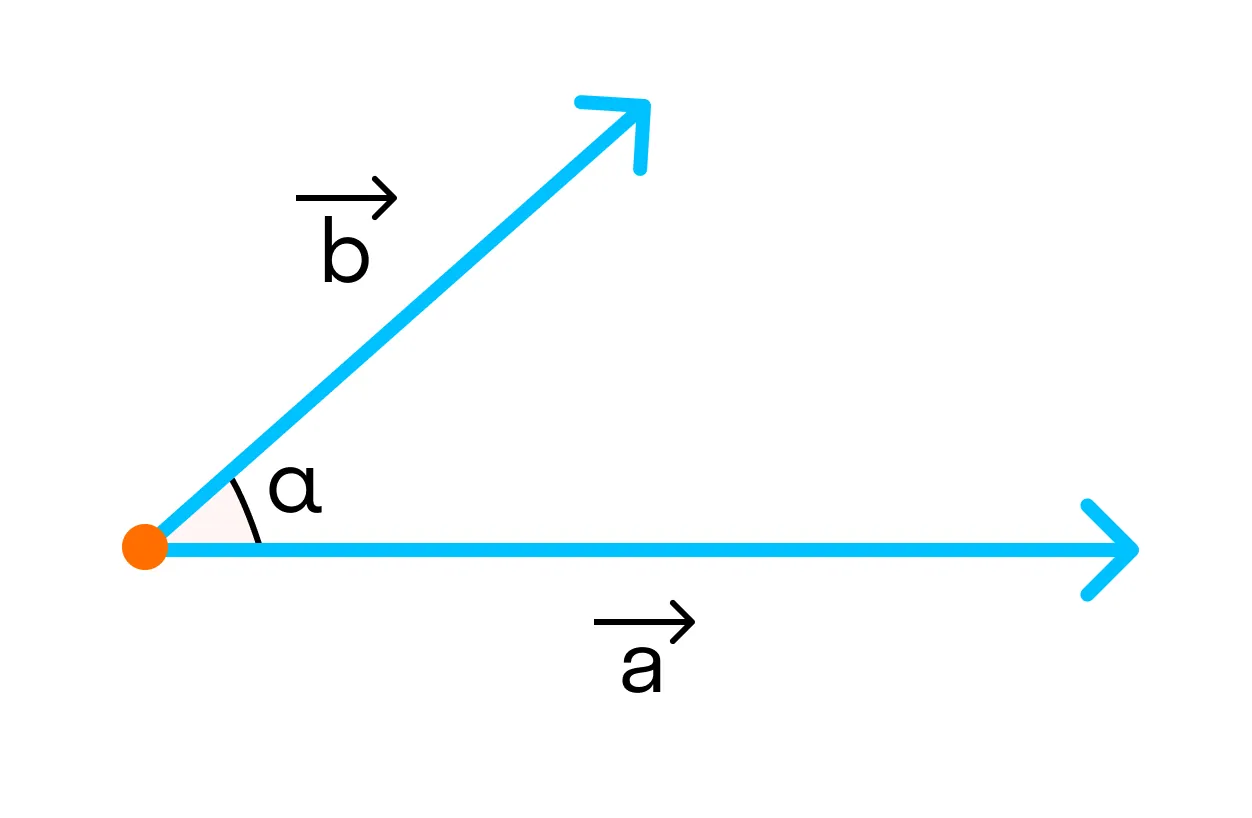
1. Если векторы сонаправлены, то угол между ними равен 0°.
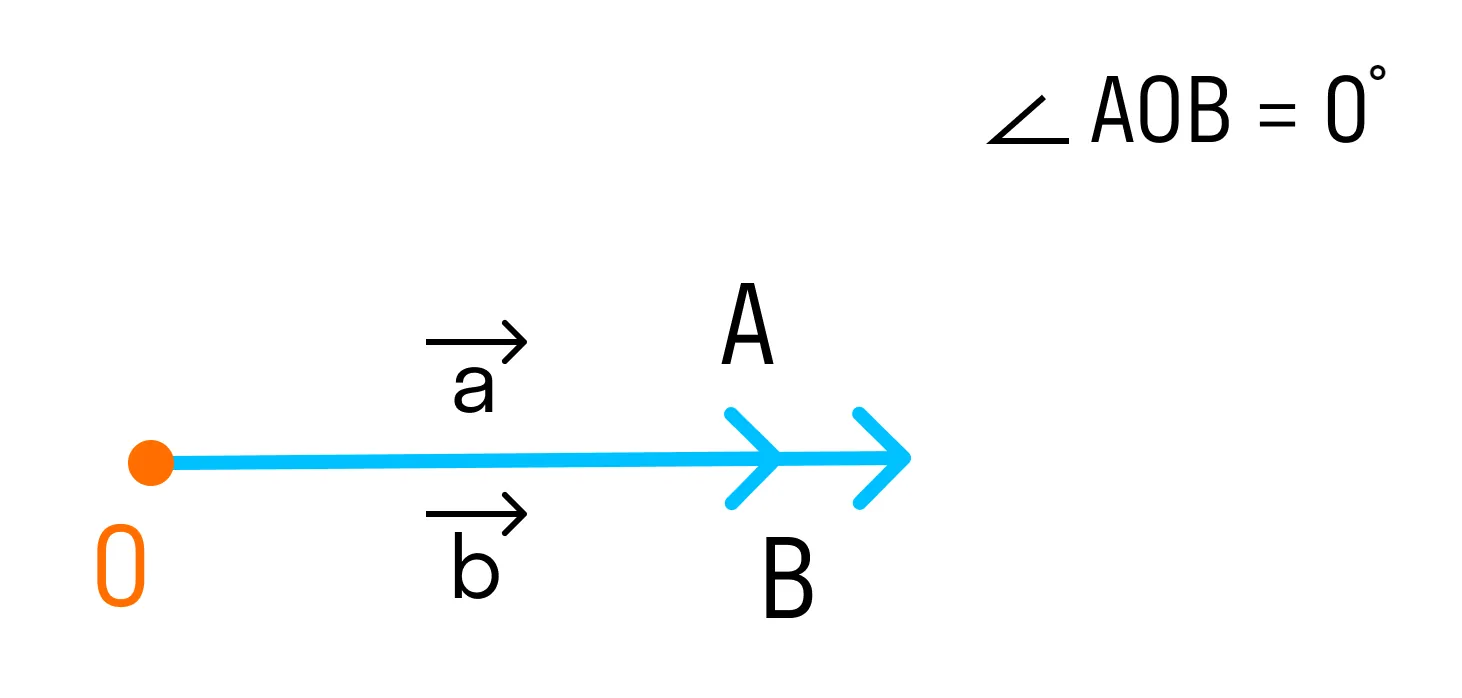
2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.
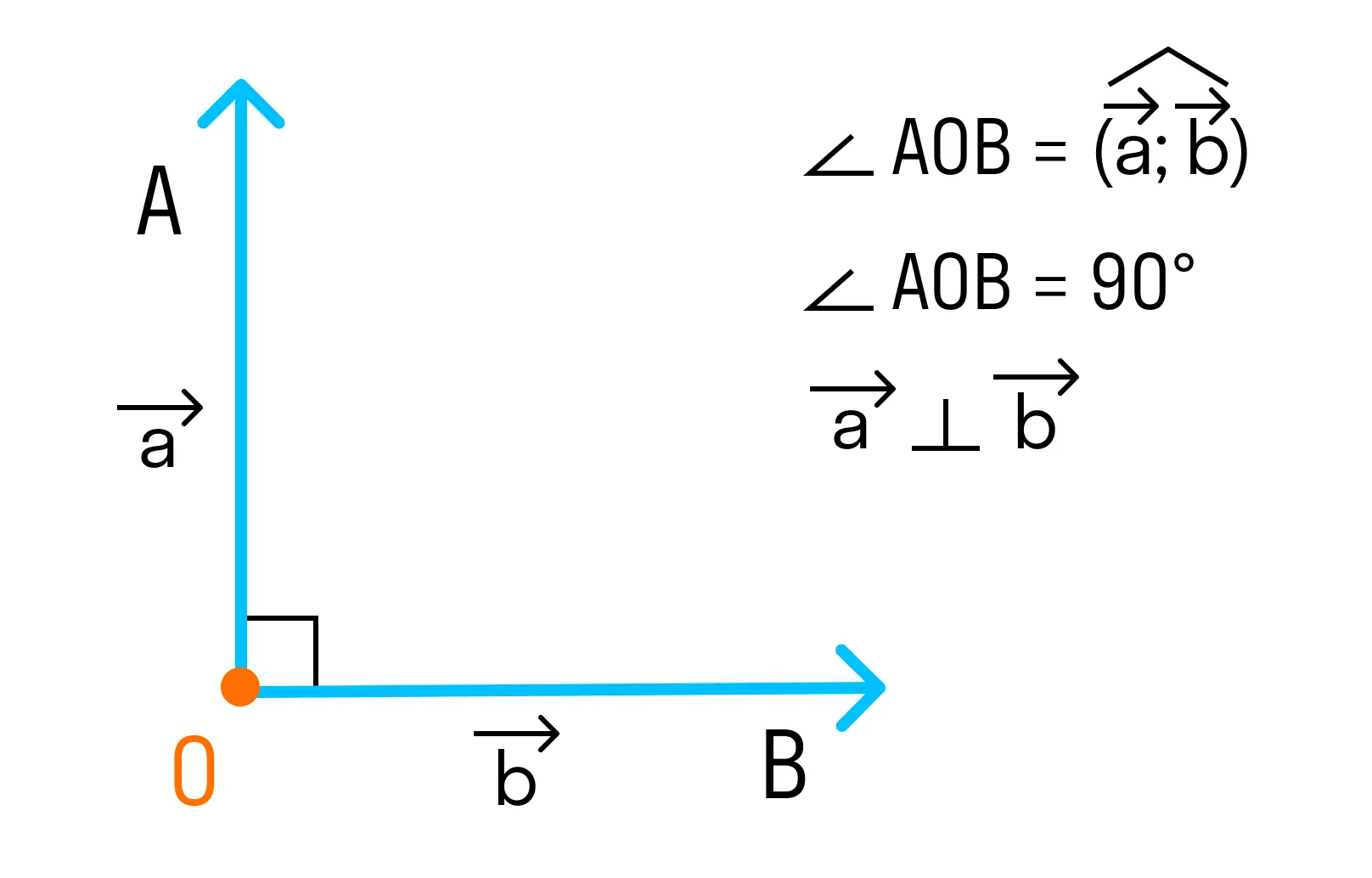
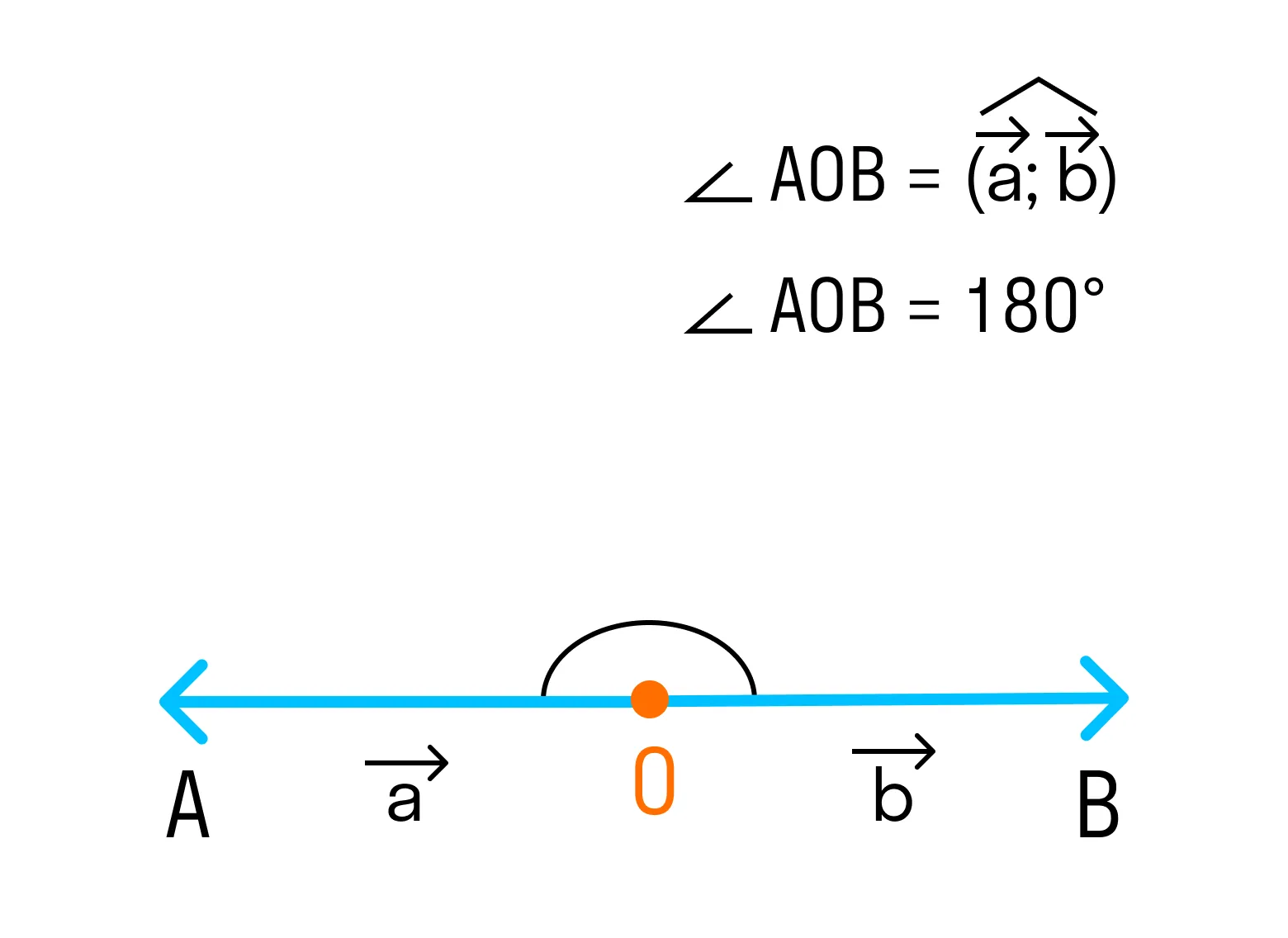
3. Если векторы направлены в разные стороны, тогда угол между ними 180°.
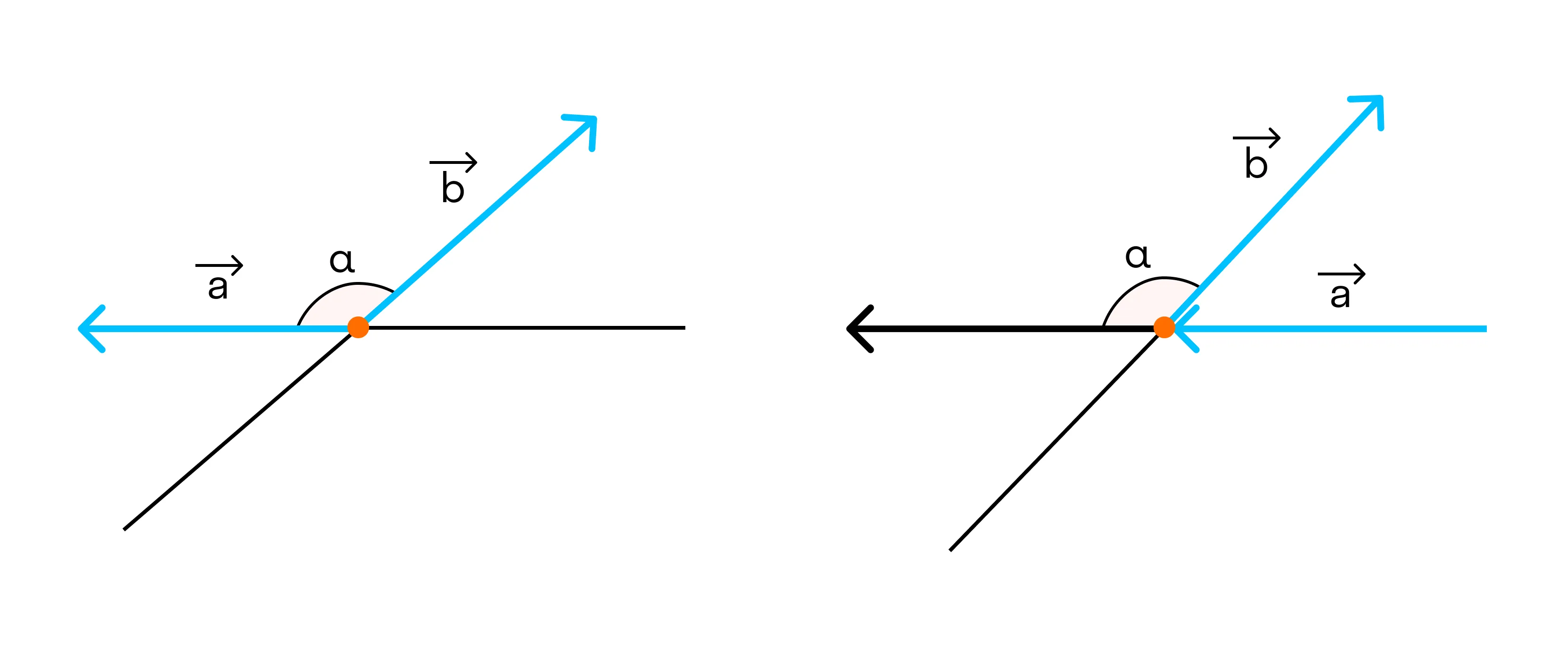
Также векторы могут образовывать тупой угол. Это выглядит так:
Получи больше пользы от Skysmart:
-
Подготовься к ОГЭ на пятёрку
-
Подготовься к ЕГЭ на высокие баллы
Записывайся на бесплатные курсы для детей
Решай задания в бесплатном тренажёре ЕГЭ
Скалярное произведение векторов
Определение скалярного произведения можно сформулировать двумя способами:
Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.
- Геометрическая интерпретация.
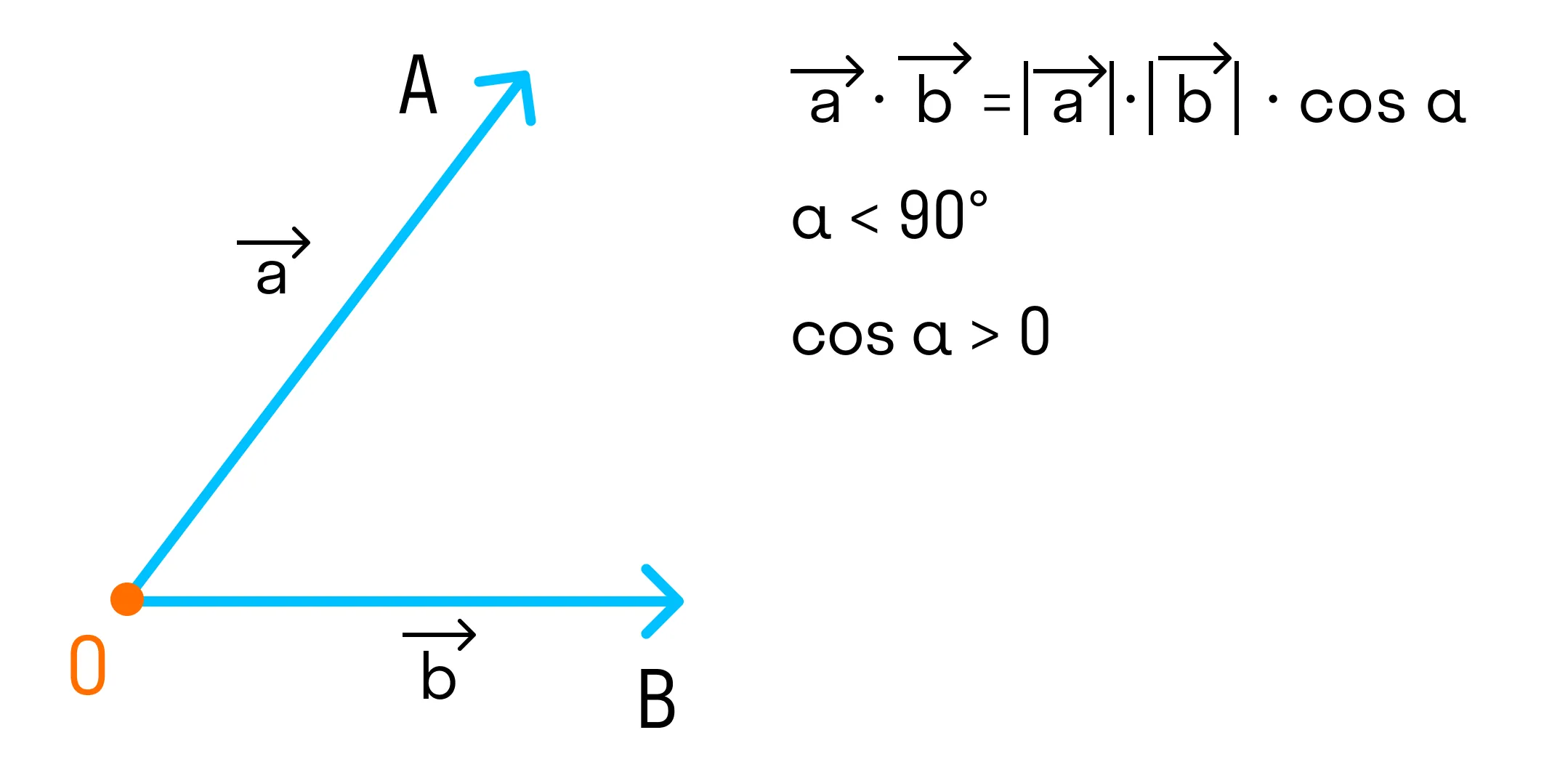
Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:
- Алгебраическая интерпретация.
Что важно запомнить про геометрическую интерпретацию скалярного произведения:
- Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, так как cosα > 0.
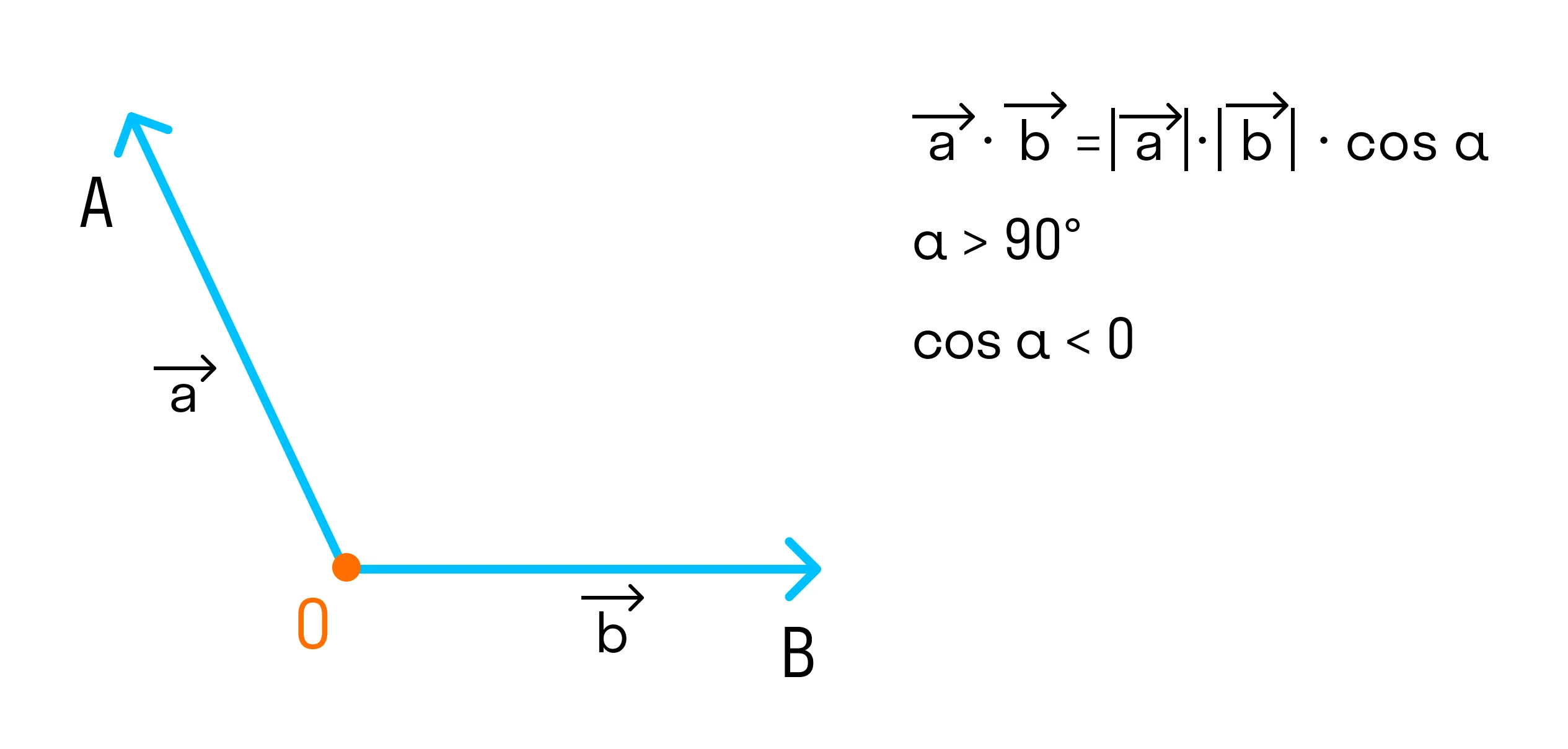
- Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как cosα < 0.
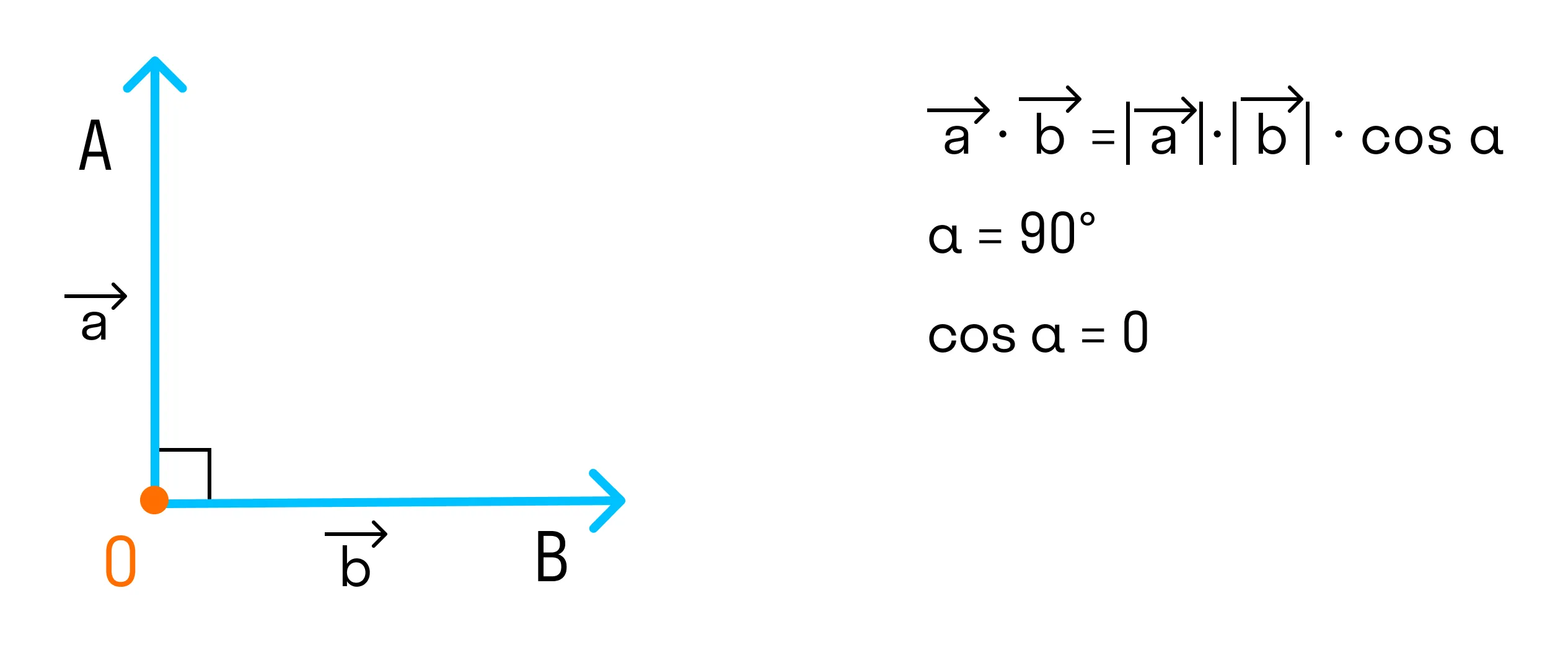
- Если угол между векторами прямой, то скалярное произведение равно 0, так как cosα = 0.
Скалярное произведение в координатах
Скалярное произведение векторов по координатам - это сумма произведений их соответствующих координат. Например, для векторов
Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.
Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов
То есть для векторов
А для векторов
В n-мерном пространстве скалярное произведение векторов a = {a1; a2; ... ; an} и b = {b1; b2; ... ; bn} можно найти по формуле:
a * b = a1 * b1 + a2 * b2 + ... + an * bn
Свойства скалярного произведения векторов
Скалярное произведение вектора самого на себя всегда больше или равно нулю. В результате получается нуль, если вектор равен нулевому вектору.
Скалярное произведение вектора самого на себя равно квадрату его модуля:
Операция скалярного произведения коммуникативна, то есть соответствует переместительному закону:
Операция скалярного умножения дистрибутивна, то есть соответствует распределительному закону:
Сочетательный закон для скалярного произведения:
Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы ортогональны, то есть перпендикулярны друг другу:
Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.
Примеры вычислений скалярного произведения
Пример 1.
Вычислите скалярное произведение двух векторов →a и →b, если их длины равны 3 и 7 соответственно, а угол между ними равен 60 градусам.
Как решаем:
У нас есть все данные, чтобы вычислить скалярное произведение по определению:
Ответ:
Пример 2.
Найти скалярное произведение векторов
Как решаем:
Используем формулу
В данном случае:
Ответ:
Пример 3.
Как найти скалярное произведение векторов
Как решаем:
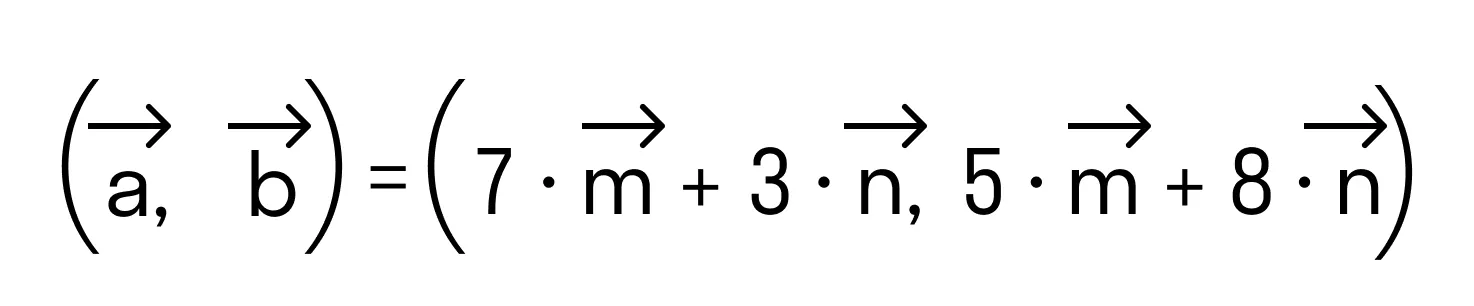
По свойству дистрибутивности скалярного произведения имеем
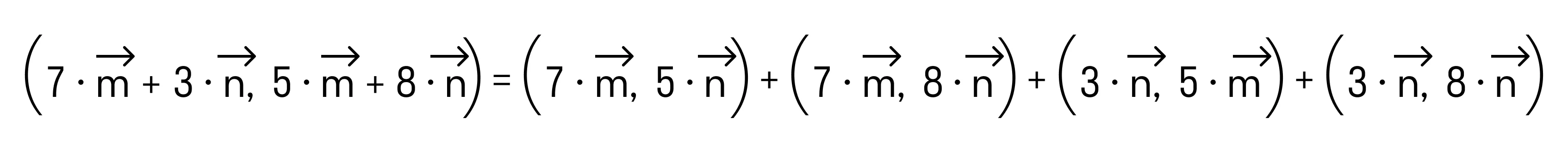
Сочетательное свойство позволяет нам вынести коэффициенты за знак скалярного произведения:
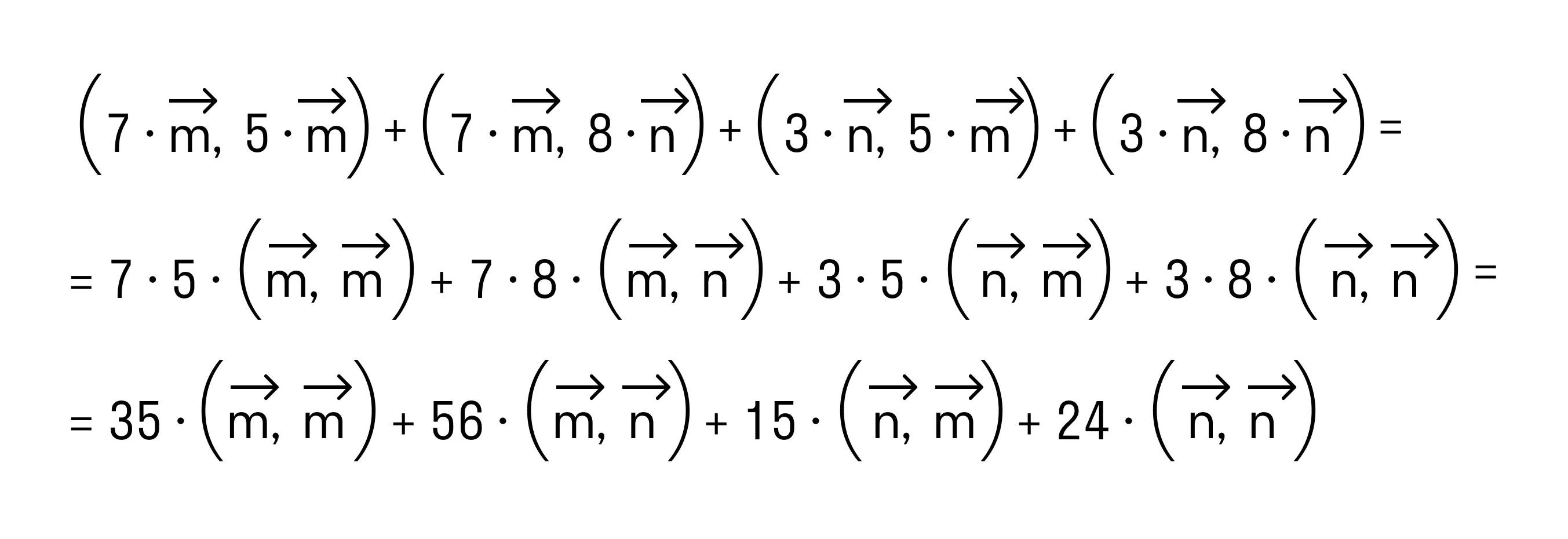
В силу свойства коммутативности последнее выражение примет вид
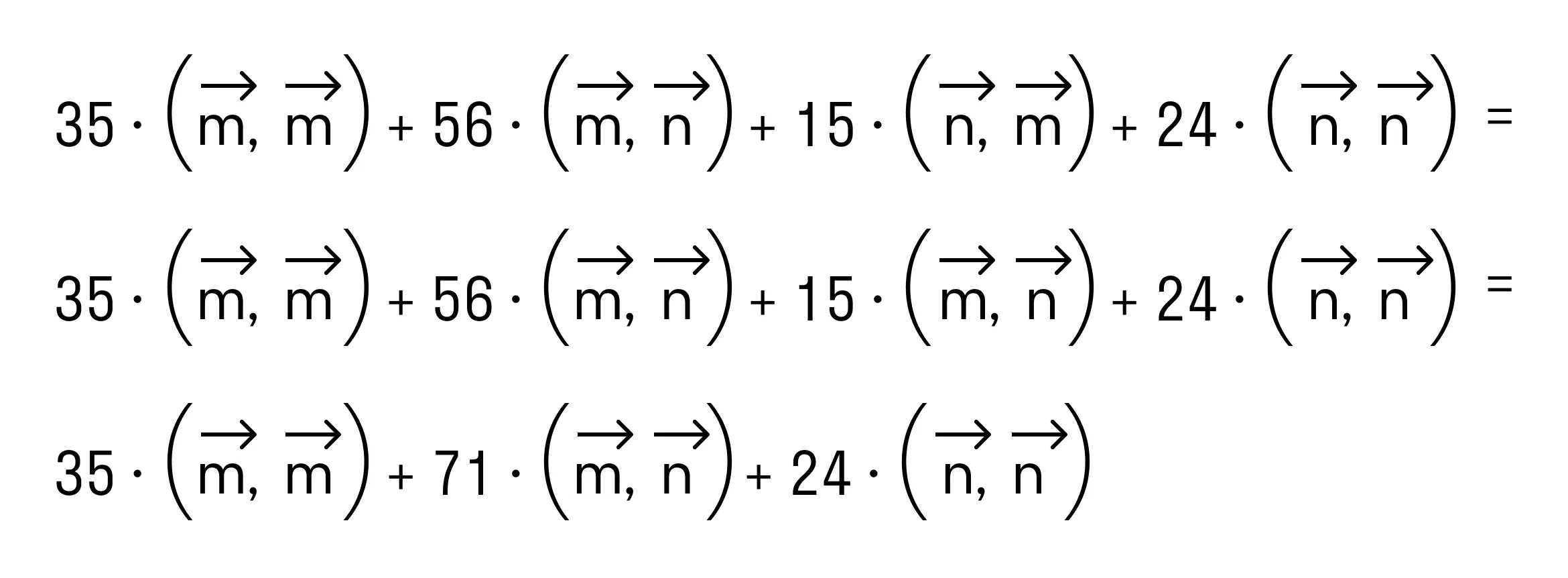
Итак, после применения свойств скалярного произведения имеем
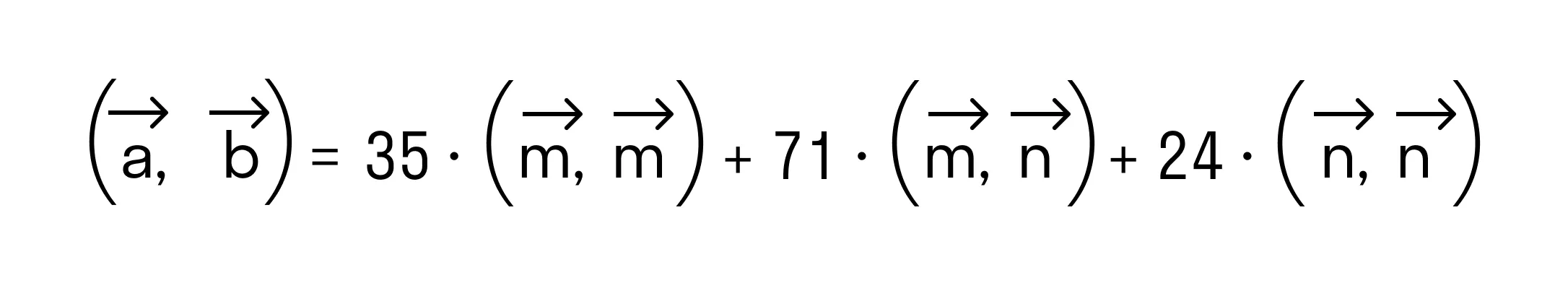
Осталось применить формулу для вычисления скалярного произведения через длины векторов и косинус угла между ними:
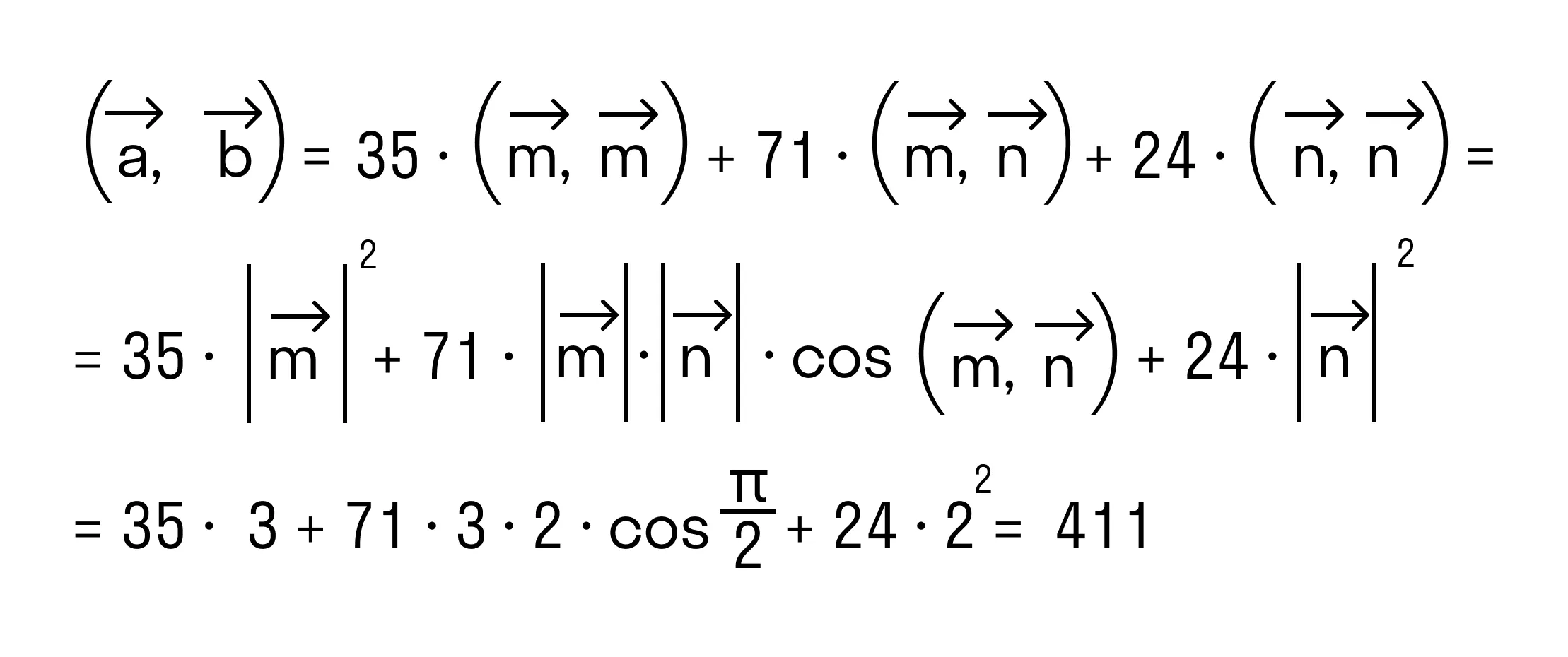
Ответ:
Пример 4.
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найти косинус угла между прямыми AB1 и BC1.
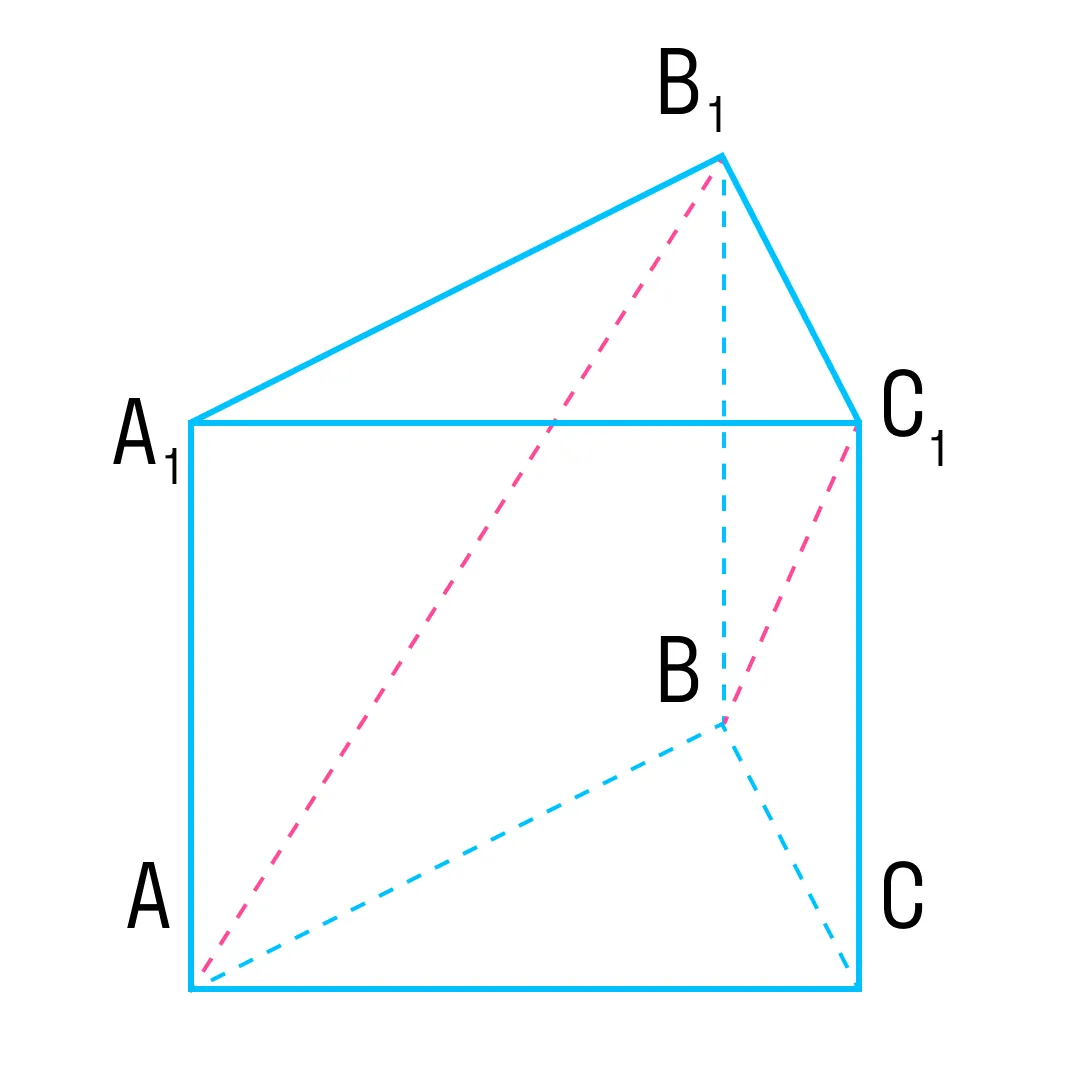
Как решаем:
Введем систему координат.
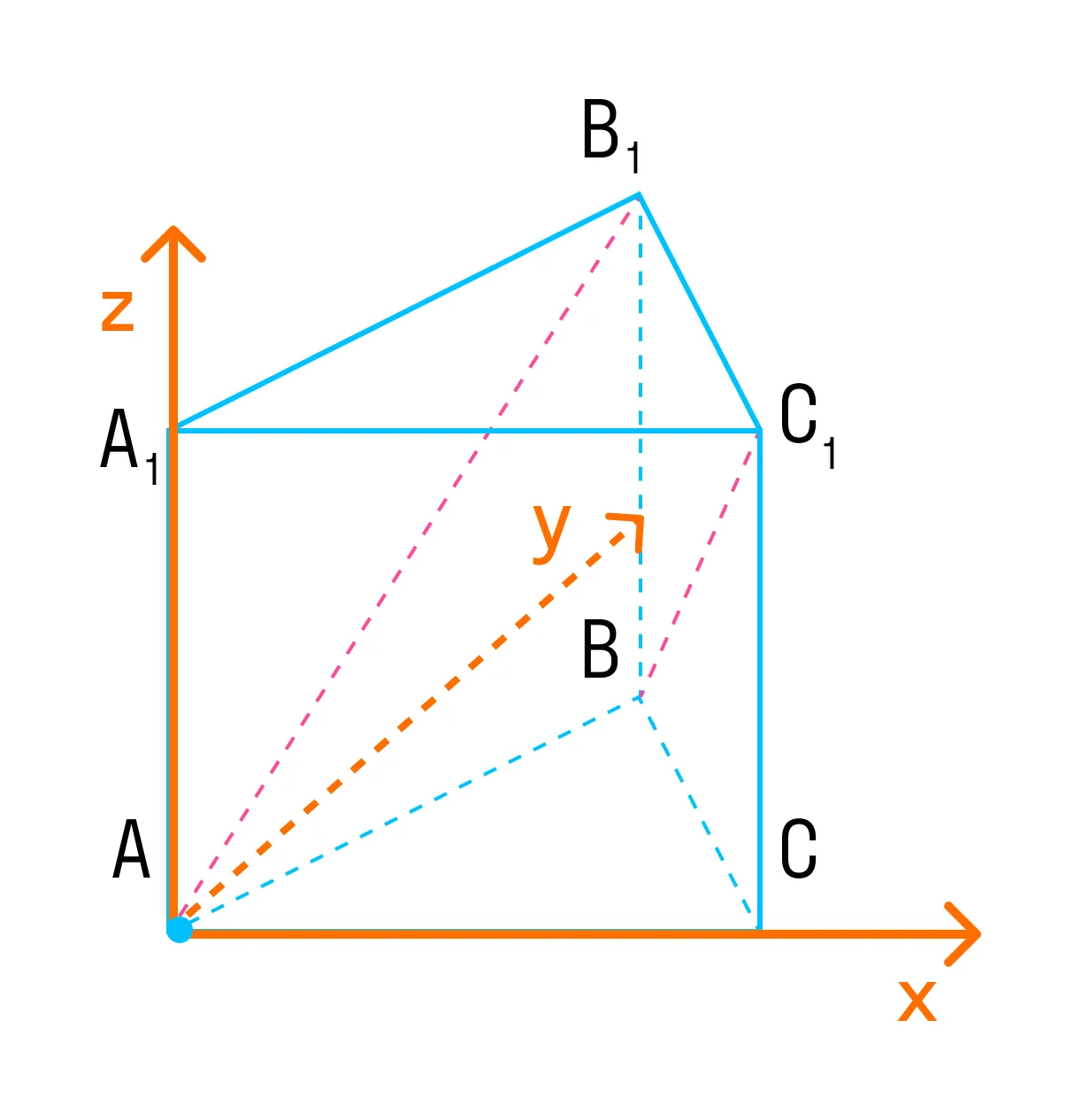
Если сделать выносной рисунок основания призмы, получим понятный плоскостной рисунок с помощью которого можно легко найти координаты всех интересующих точек.
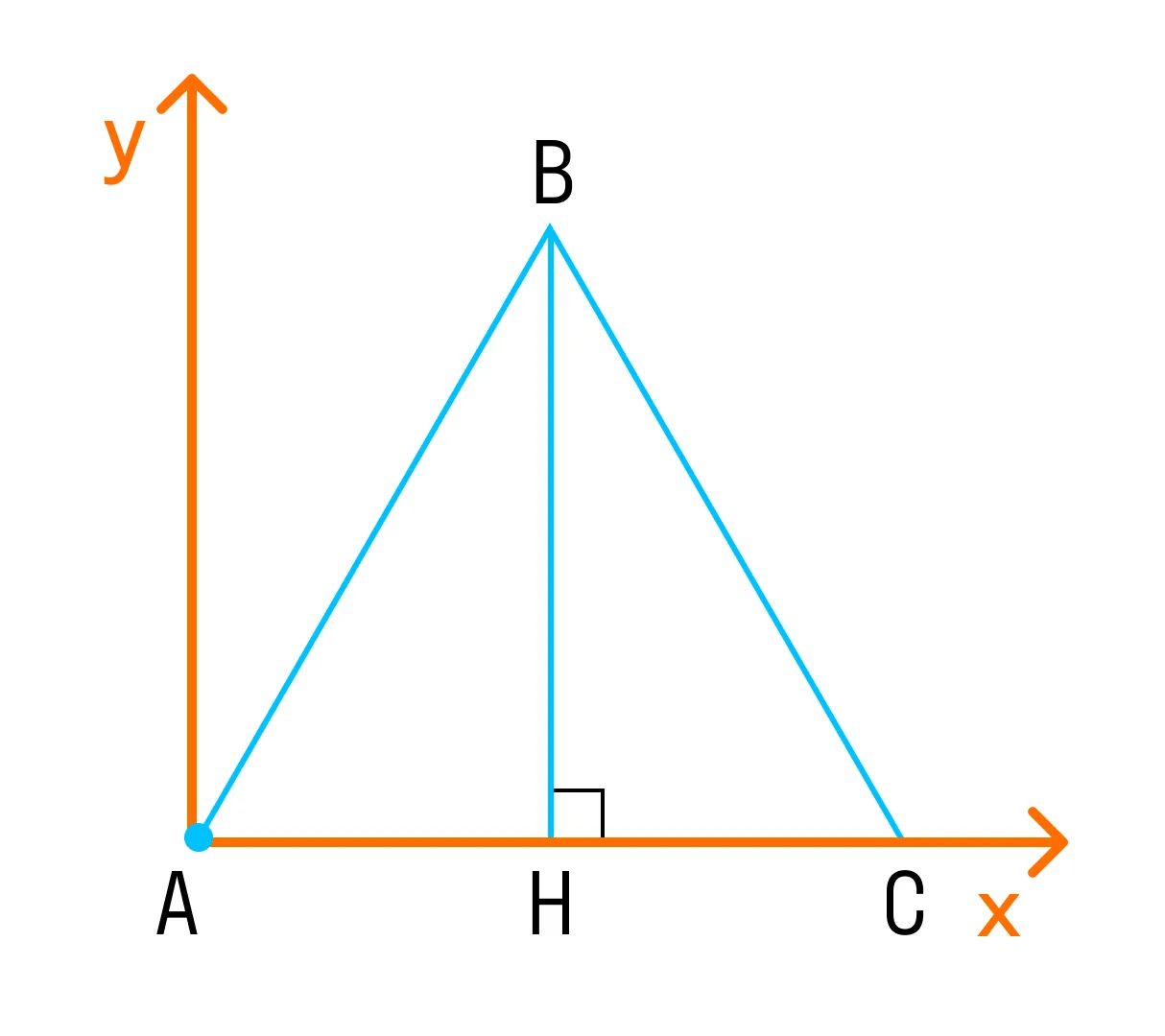
Точка А имеет координаты (0;0;0). Точка С — (1;0;0). Точка В — (1/2;√3/2;0). Тогда точка В1 имеет координаты (1/2;√3/2;1), а точка С1 – (1;0;1).
Найдем координаты векторов
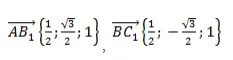
Найдем длины векторов
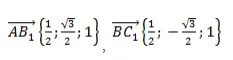
Найдем скалярное произведение векторов через их координаты
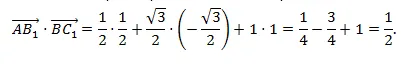
Найдем косинус угла между прямыми AB1 и BC1:
Ответ: 1/4.
Пример 5.
а) Проверить ортогональность векторов:
б) Выяснить, будут ли перпендикулярными отрезки KL и MN, если K(3;5), L(-2;0), M(8;-1), N(1;4).
Как решаем:
а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение:
б) Здесь речь идёт об обычных отрезках плоскости, а задача всё равно решается через векторы. Найдем их:
Вычислим их скалярное произведение:
Обратите внимание на два существенных момента:
- В данном случае нас не интересует конкретное значение скалярного произведения, важно, что оно не равно нулю.
- В окончательном выводе подразумевается, что если векторы не ортогональны, значит, соответствующие отрезки тоже не будут перпендикулярными. Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках, что они не перпендикулярны.
Ответ: а)
Пример 6.
Даны три вершины треугольника A(-1; 0), B(3; 2), C(5; -4). Найти угол при вершине B — ∠ABC.
Как решаем:
По условию чертеж выполнять не требуется, но для удобства можно сделать:
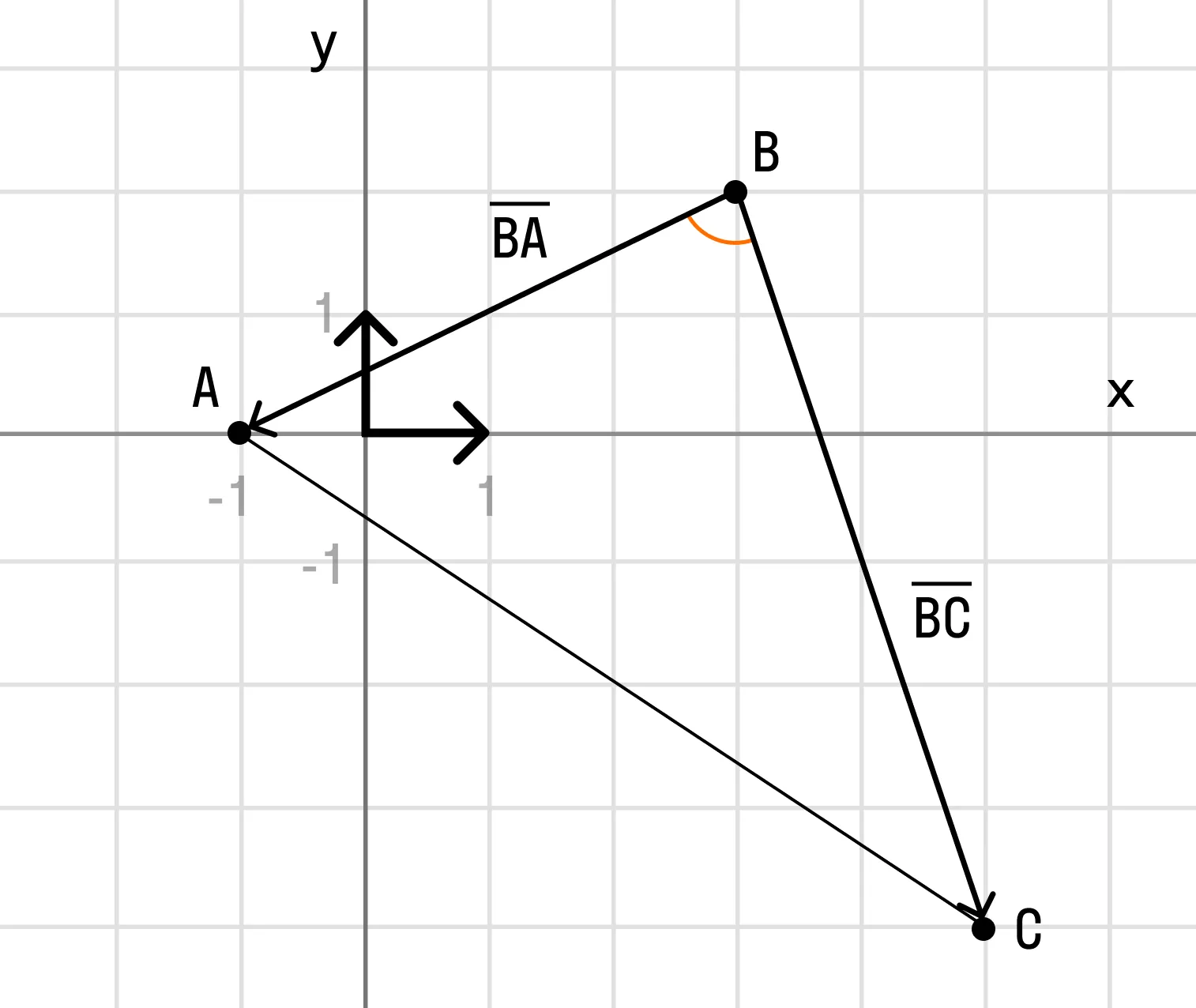
Требуемый угол ∠ABC помечен красной дугой. Сразу вспоминаем школьное обозначение угла: ∠ABC — особое внимание на среднюю букву B — это и есть нужная нам вершина угла. Для краткости можно также записать просто ∠B.
Из чертежа видно, что угол ∠ABC треугольника совпадает с углом между векторами
Найдем векторы:
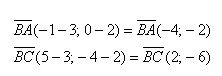
Вычислим скалярное произведение:
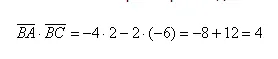
Вычислим длины векторов:
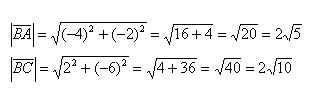
Найдем косинус угла:
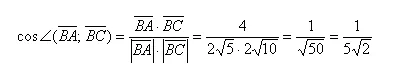
Когда такие примеры не будут вызывать трудностей, можно начать записывать вычисления в одну строчку:
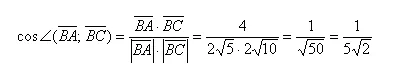
Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.
Найдём сам угол:
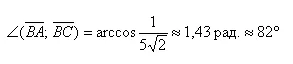
Если посмотреть на чертеж, то результат действительно похож на правду. Для проверки угол также можно измерить и транспортиром.
Ответ: ∠ABC = arccos(1/5√2) ≈1,43 рад. ≈ 82°
Важно не перепутать, что в задаче спрашивалось про угол треугольника, а не про угол между векторами. Поэтому указываем точный ответ: arccos(1/5√2) и приближенное значение угла: ≈1,43 рад. ≈ 82°, которое легко найти с помощью калькулятора.
А те, кому мало и хочется еще порешать, могут вычислить углы ∠A, ∠C, и убедиться в справедливости канонического равенства ∠A + ∠B + ∠C = 180°.




















