Вписанная и описанная окружность

Вписанная окружность

Вписанная окружность — это окружность, которая касается всех сторон многоугольника изнутри.

Описанный многоугольник — многоугольник, в который вписана окружность.

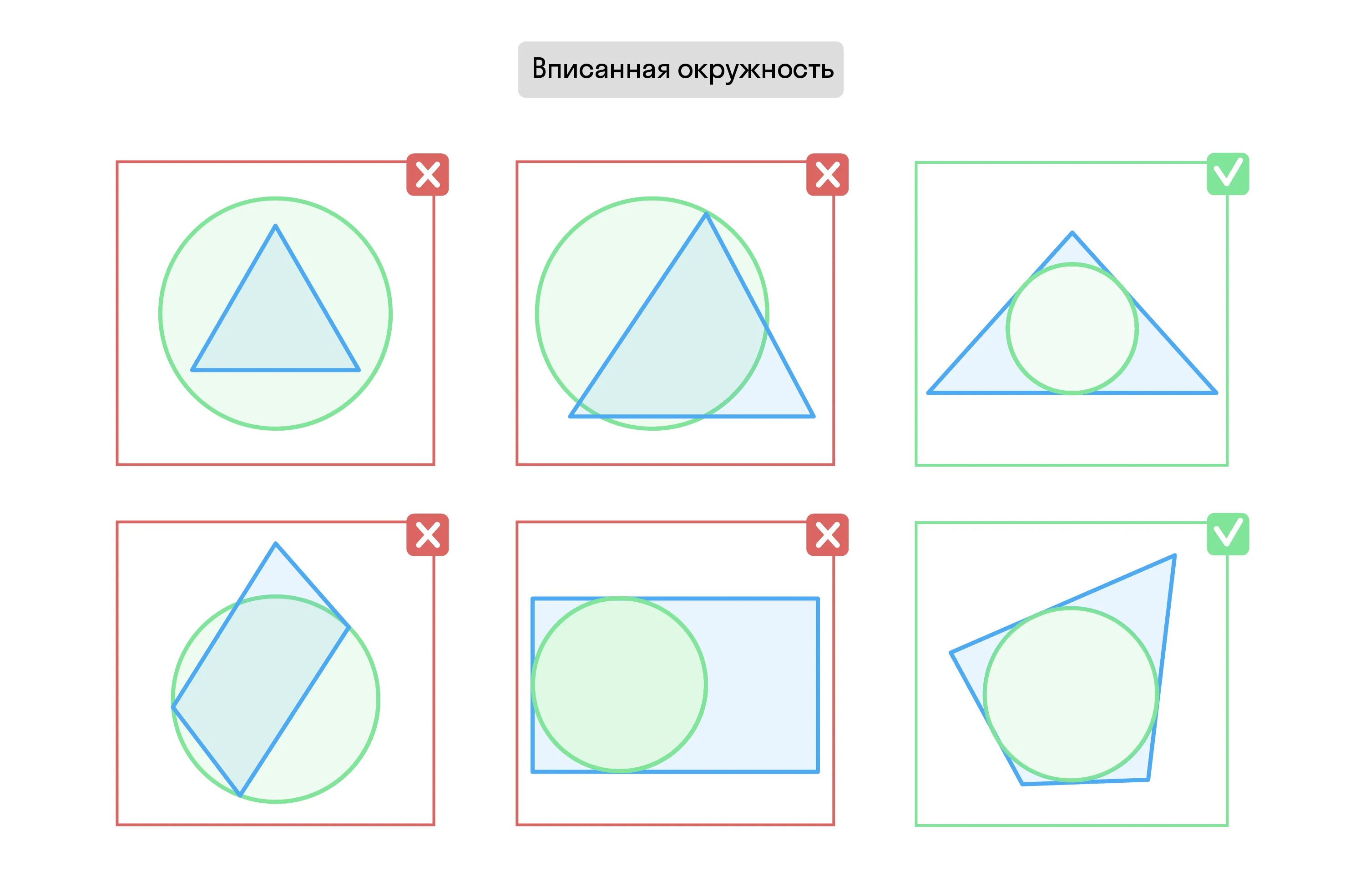
Окружность может быть вписана:

• в любой треугольник;

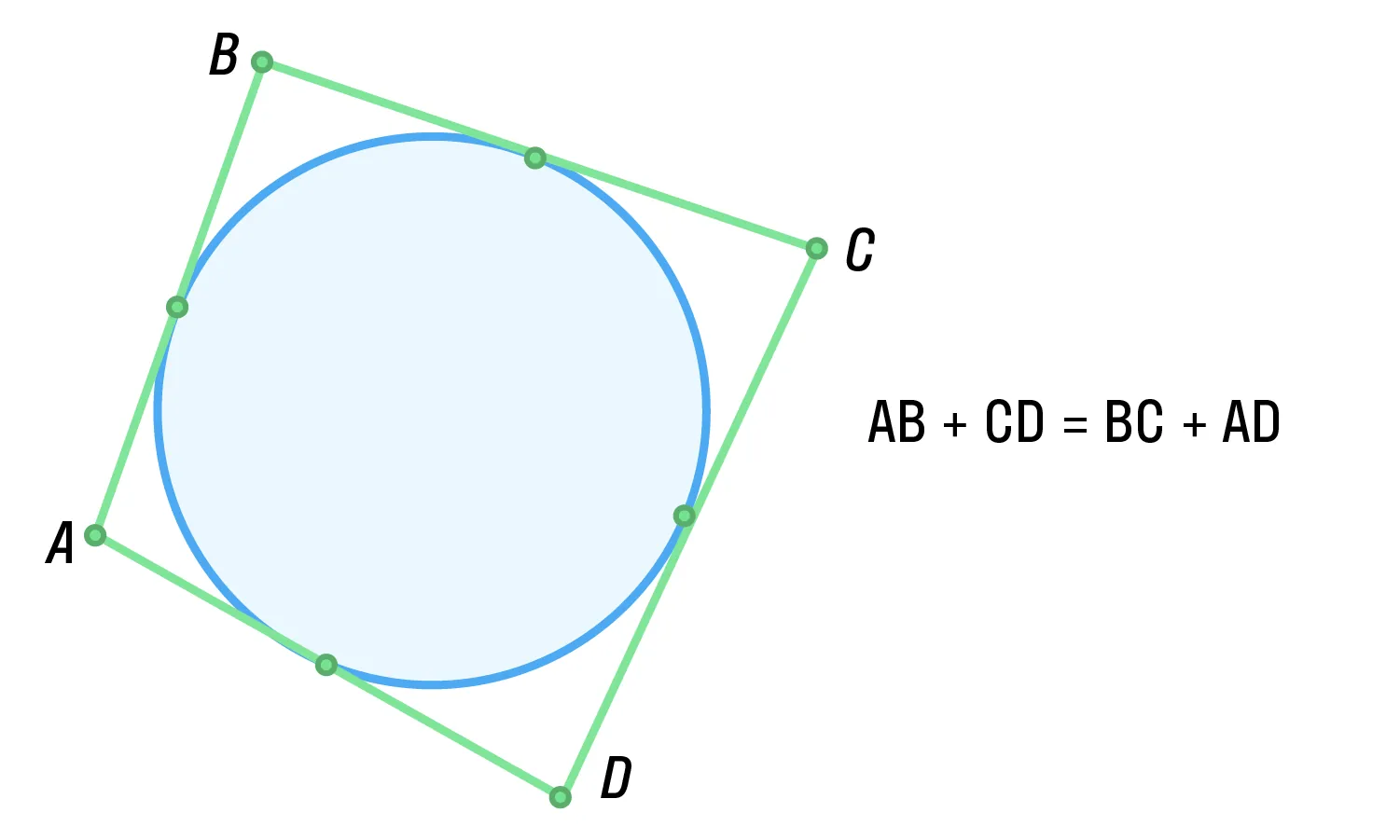
• четырёхугольник, суммы противоположных сторон которого равны;

  

• в правильный многоугольник , т. е. в такой, у которого равны все стороны и все углы.

  

Свойства и формулы для вписанной окружности

Вписанная окружность и треугольник

• В любой треугольник можно вписать окружность, и только одну.

  

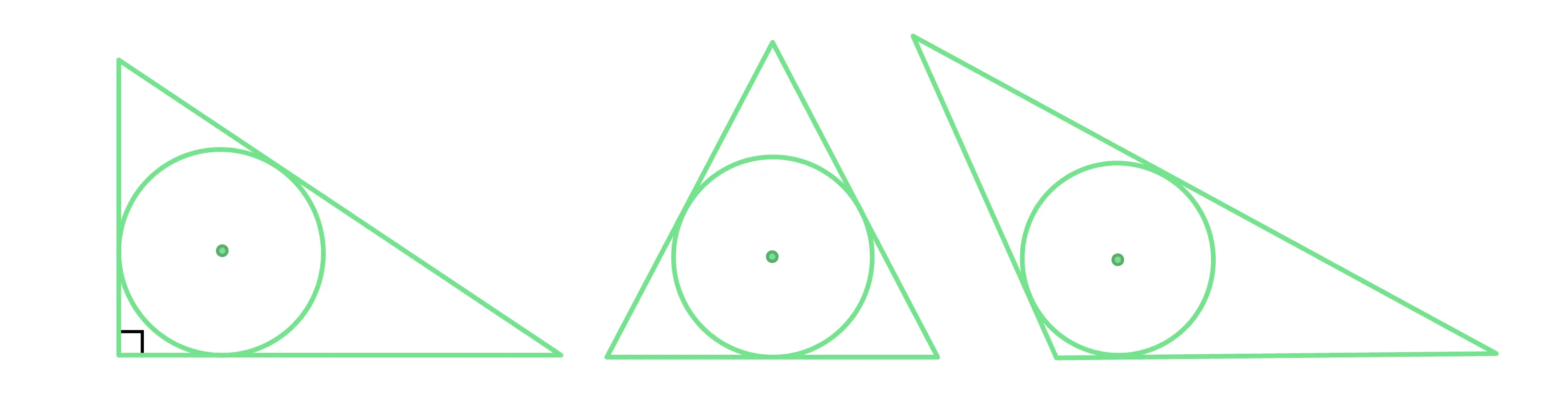
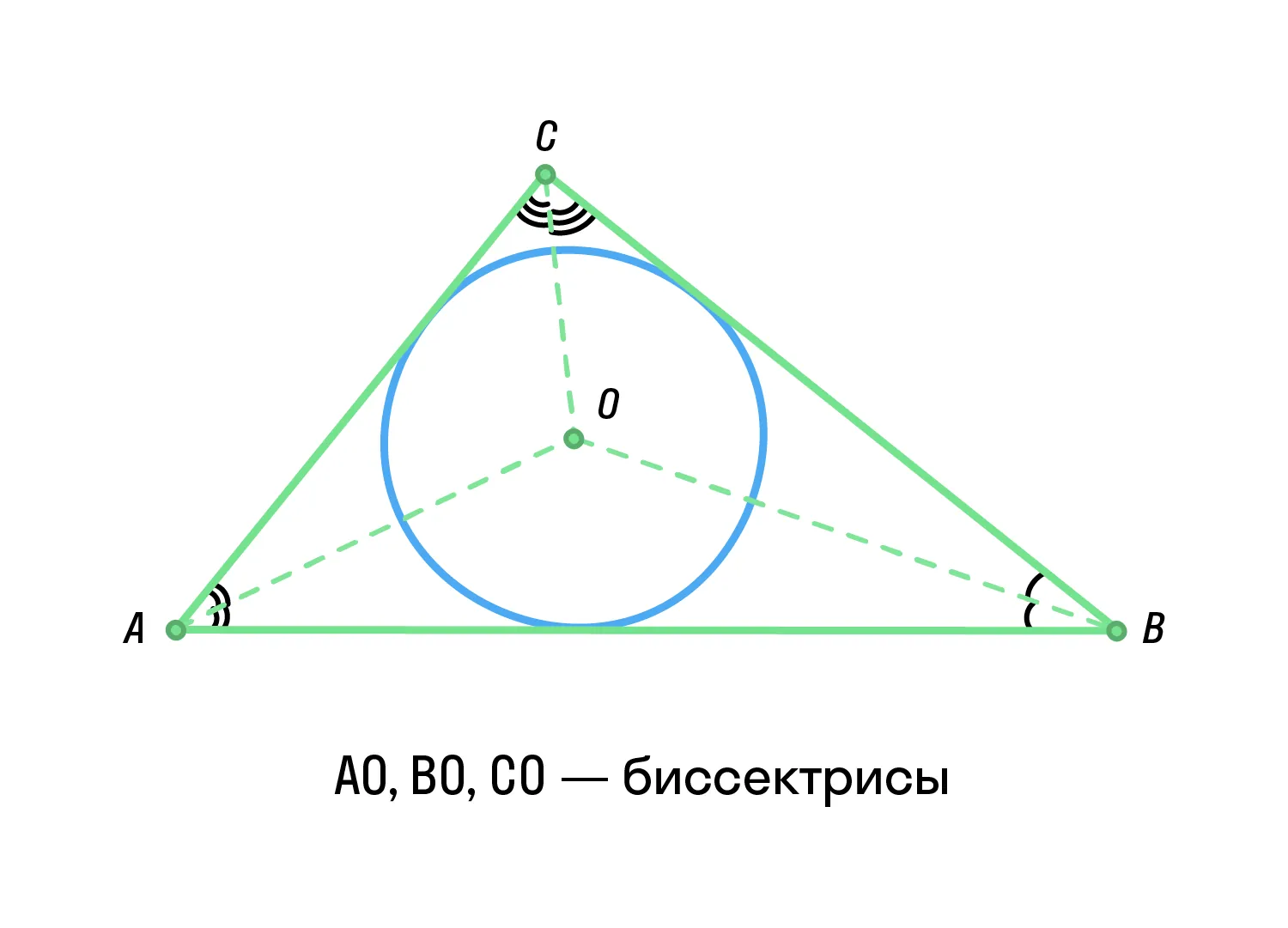
• Если окружность вписана в треугольник, её центр будет совпадать с точкой пересечения биссектрис углов треугольника.

  

• Найти радиус окружности, вписанной в треугольник, можно через отношение площади этого треугольника и его полупериметра: , где — полупериметр.

• Радиус окружности, вписанной в прямоугольный треугольник, можно рассчитать по формуле .

• Для равностороннего треугольника часто используют дополнительную формулу через длину его стороны: . Её легко обосновать через теорему Пифагора: попробуйте сделать это самостоятельно!

Что ещё может понадобиться для решения задач на окружность, вписанную в треугольник?

Обратите внимание, что стороны треугольника будут являться . Согласно правилу, отрезки касательных, проведённых из одной точки, равны и составляют прямые углы с прямой, проходящей через эту точку и центр окружности.

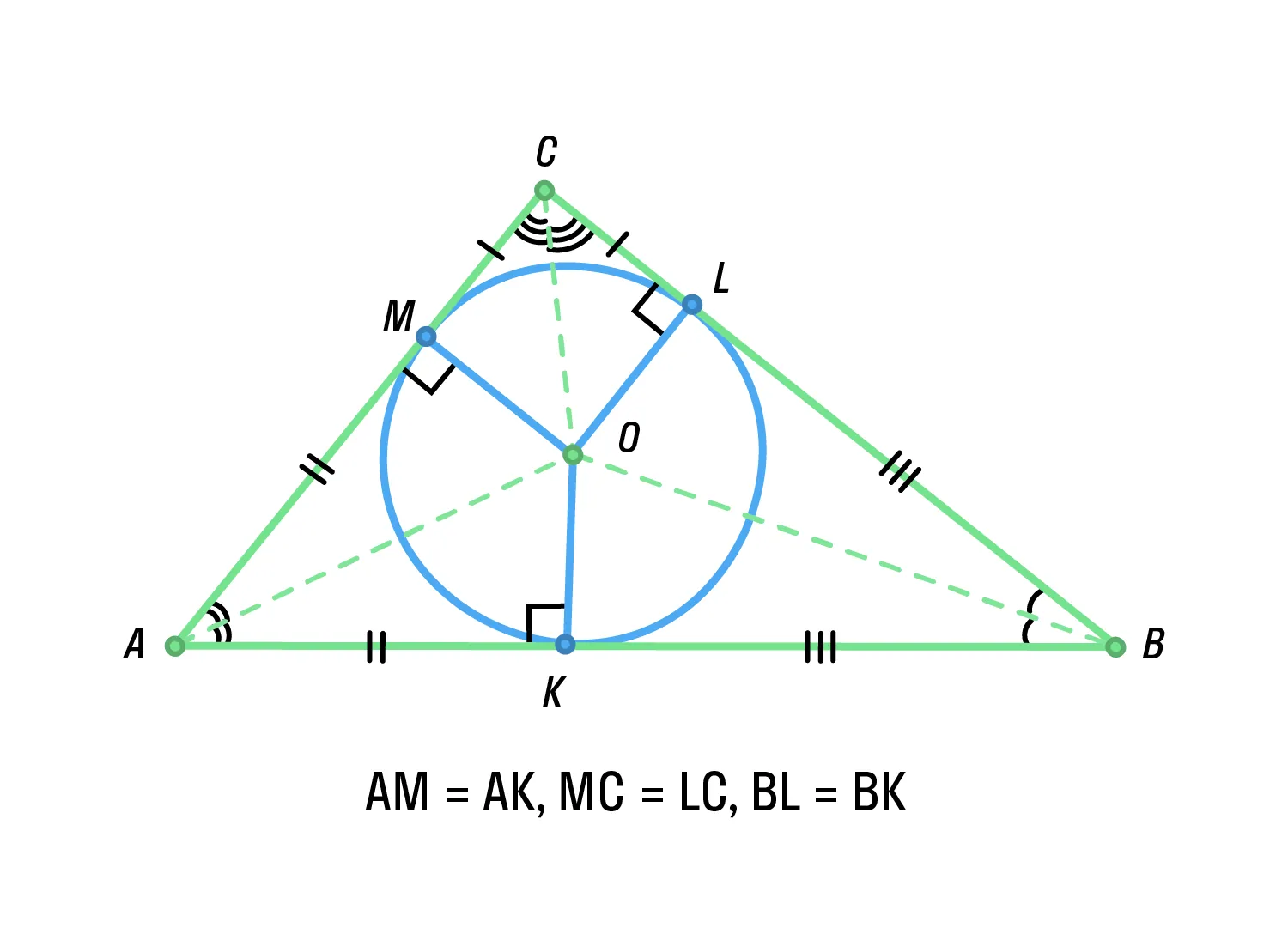
Вписанная окружность и четырёхугольник

• Окружность можно вписать в ромб, квадрат, некоторые трапеции, но нельзя в параллелограмм и прямоугольник (т. к. согласно свойству, суммы противоположных сторон описанного четырёхугольника должны быть равны).

• Центр окружности, вписанной в четырёхугольник — это точка пересечения биссектрис углов этого четырёхугольника.

  

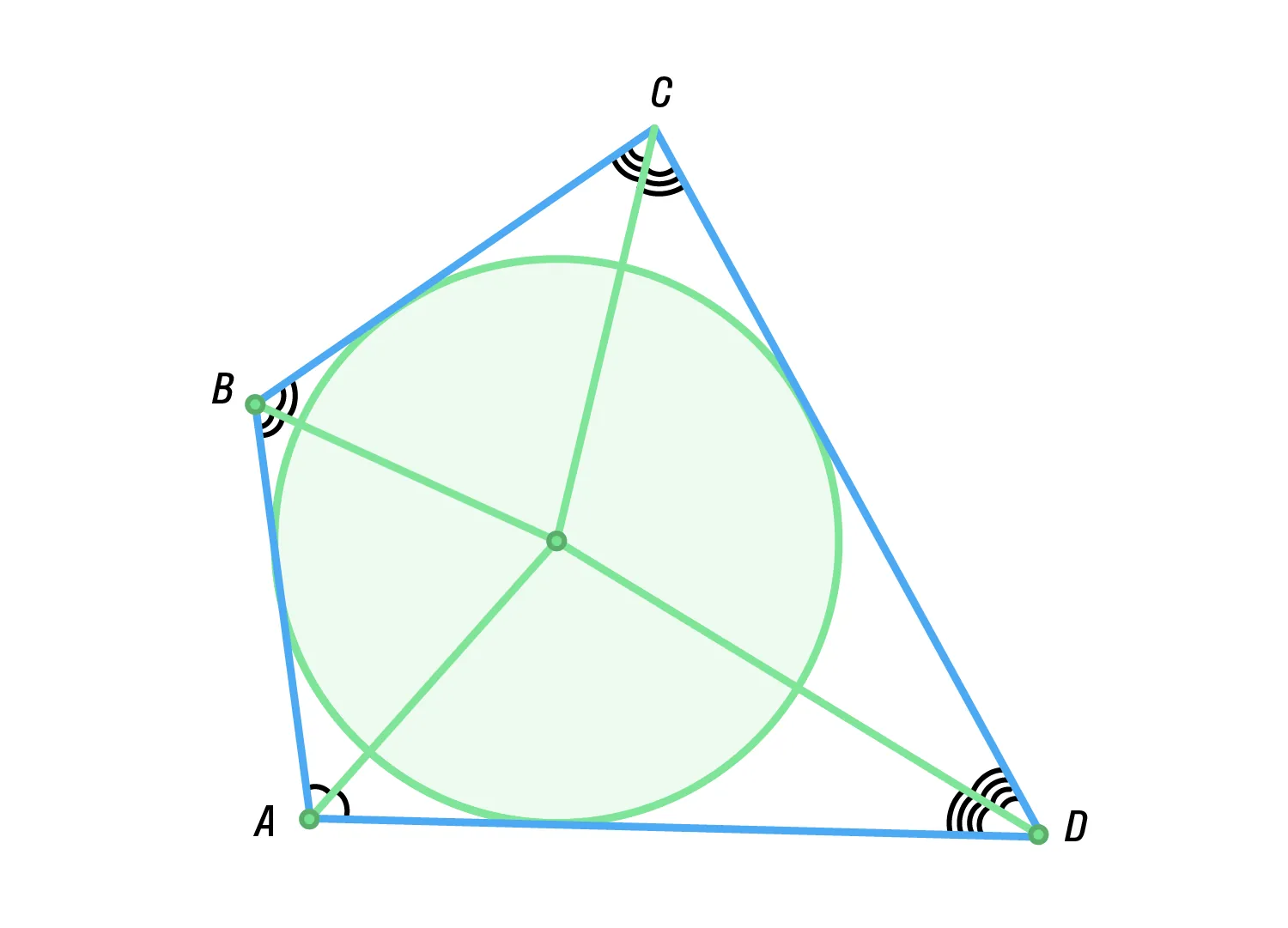
• Радиус вписанной в квадрат окружности можно рассчитать по формуле: , где а — сторона квадрата.

• Для описанного ромба можно использовать формулу , где h — высота ромба, или , где a — сторона ромба, d₁ и d₂ — диагонали ромба.

• Универсальная формула, подходящая для окружности, вписанной в любой четырёхугольник: , где — полупериметр.

Вписанная окружность и n-угольник

• Центр правильного многоугольника совпадает с центром вписанной в него окружности.

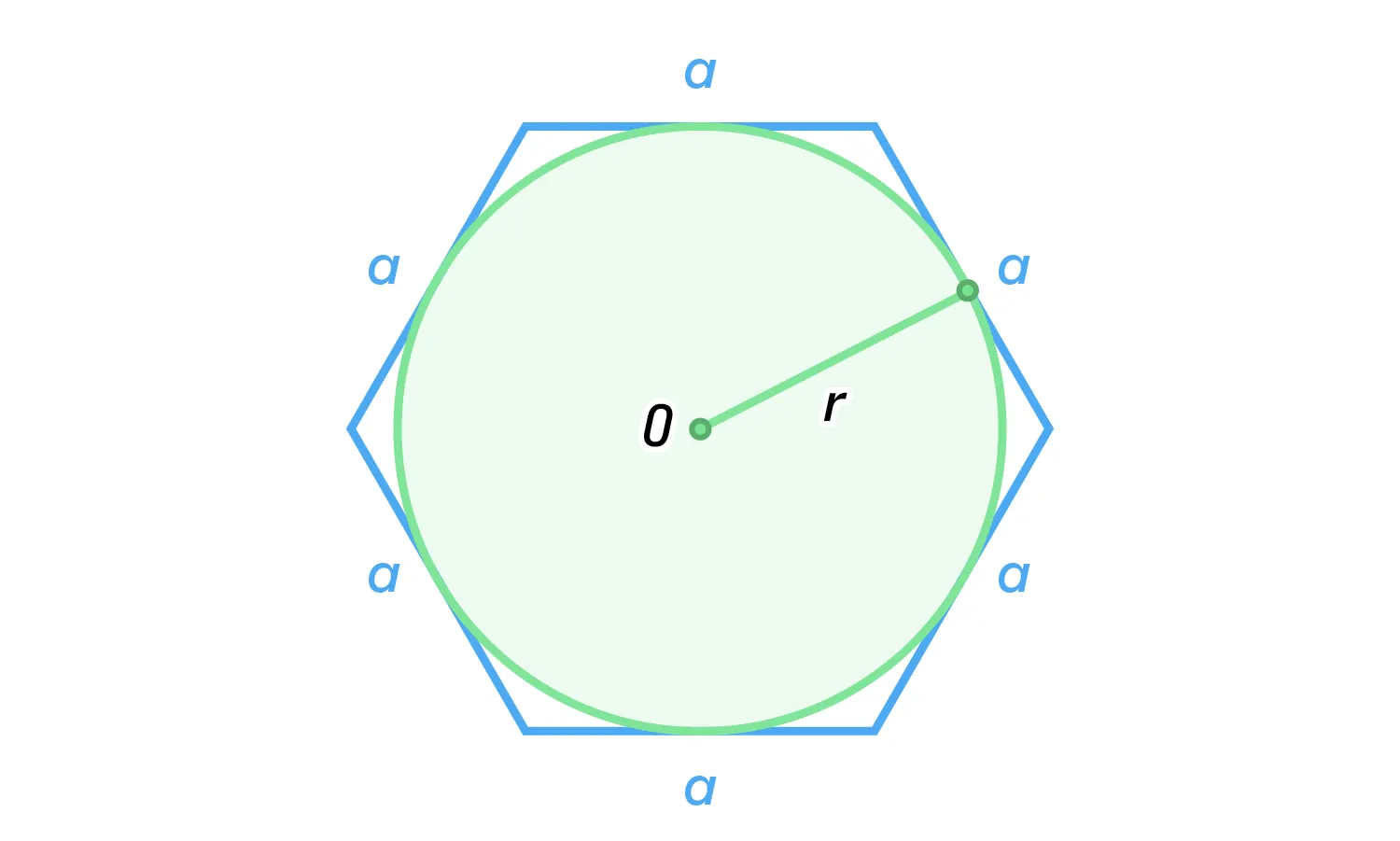
• Окружность, вписанная в правильный n-угольник, касается сторон многоугольника в их серединах.

  

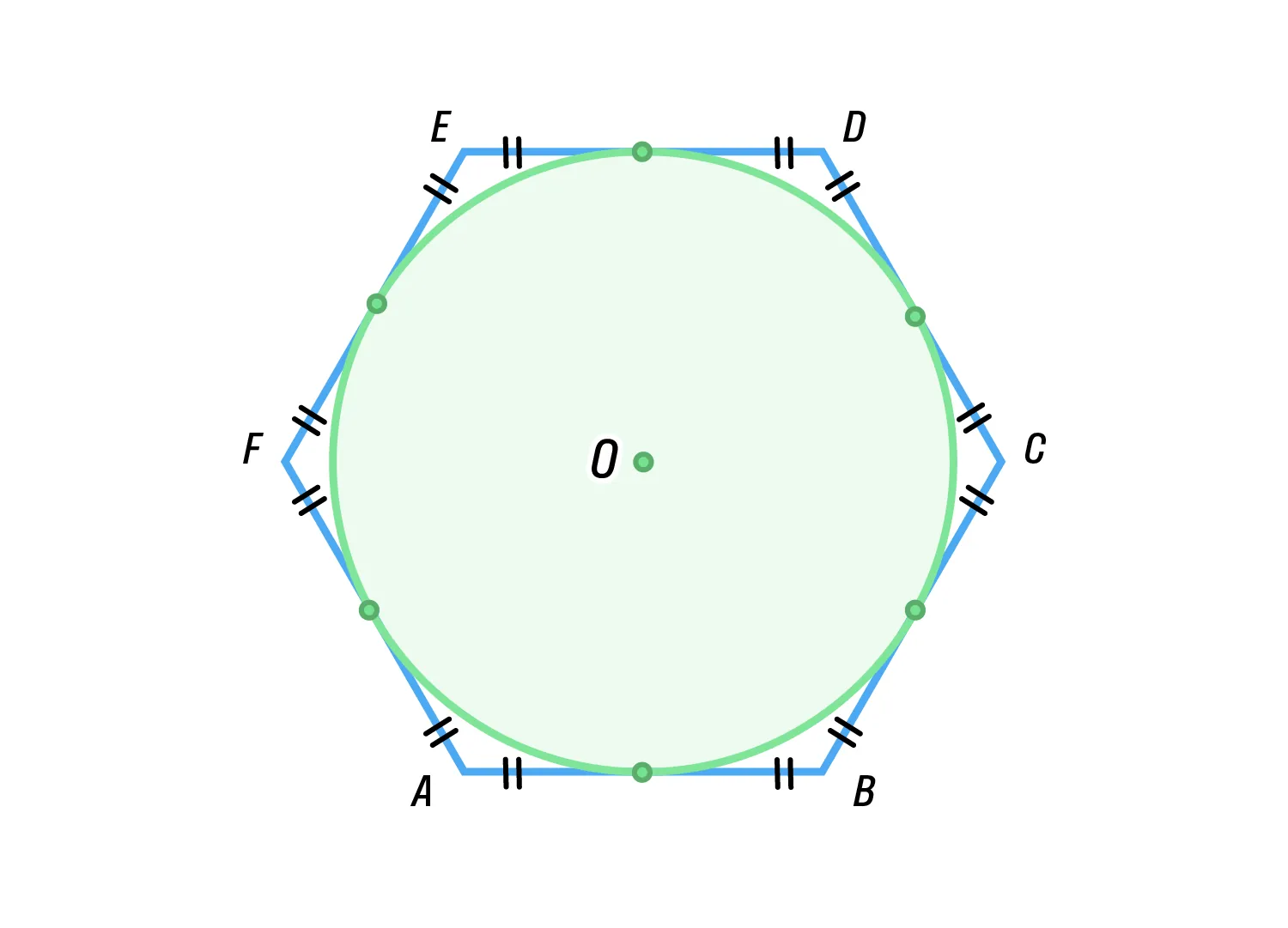
• Сторона правильного многоугольника может быть найдена по формуле: .

• Радиус окружности, которая вписана в правильный шестиугольник, находится по формуле .

170K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Описанная окружность

Описанная окружность — это окружность, содержащая все вершины n-угольника, т. е. все вершины лежат на окружности.

Вписанный многоугольник — многоугольник, около которого описана окружность.

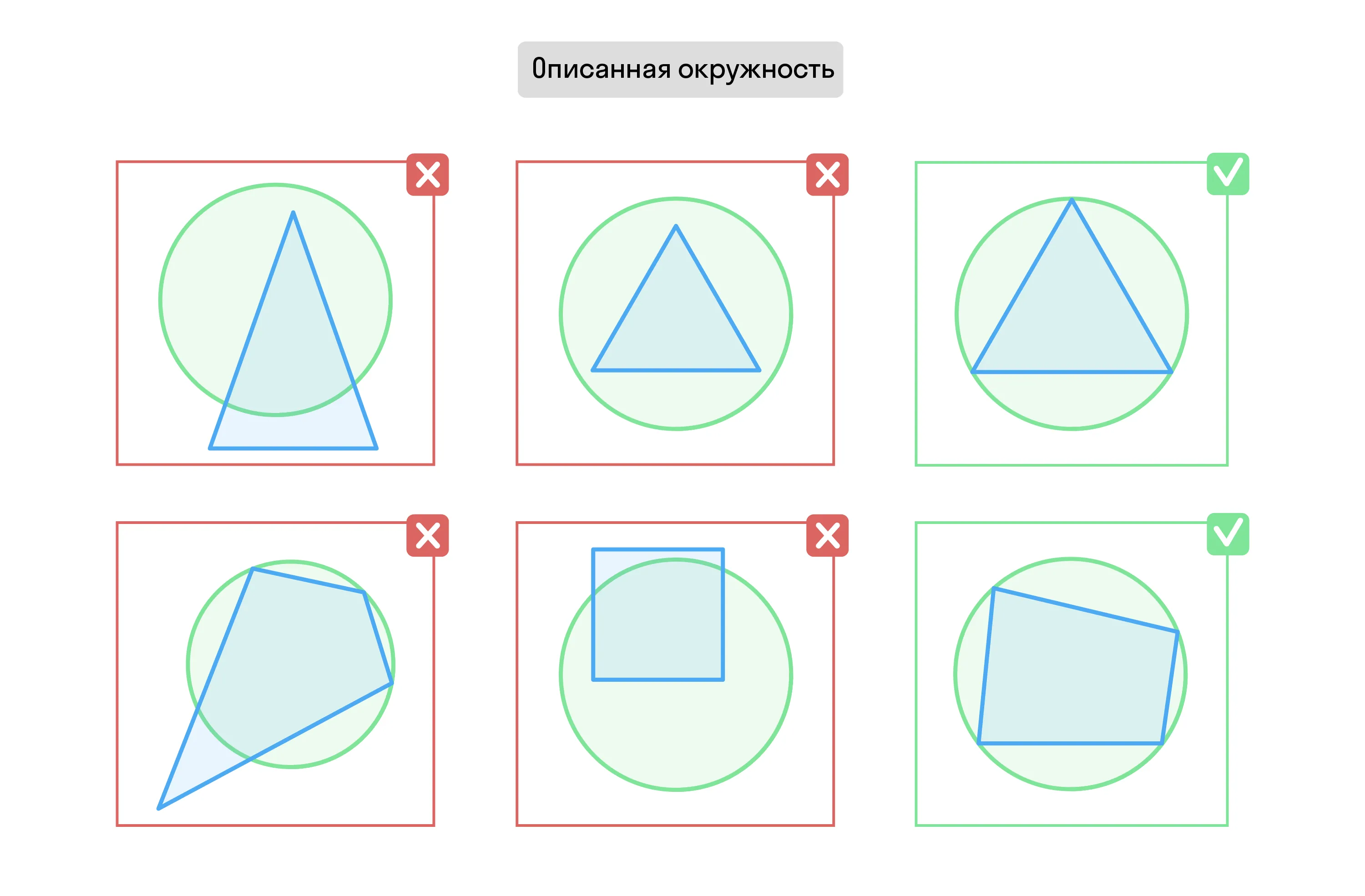
Окружность можно описать около:

• любого треугольника;

• четырёхугольника, у которого суммы противоположных углов равны;

  

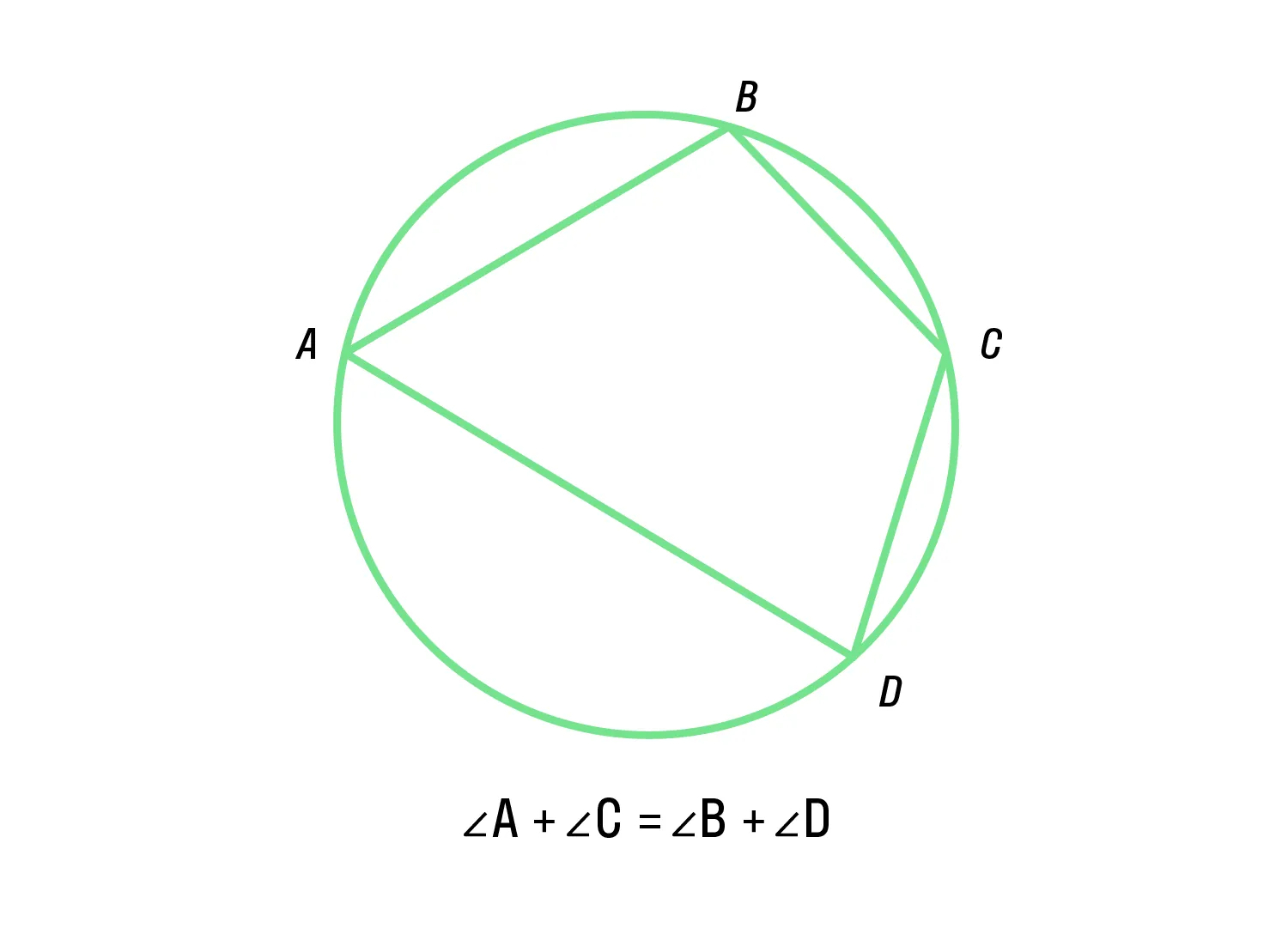
• правильного многоугольника, т. е. такого, у которого равны все стороны и все углы.

Свойства и формулы для описанной окружности

Описанная окружность и треугольник

• Любой треугольник можно описать окружностью, и только одной.

• Центр окружности, описанной около треугольника, — это точка пересечения серединных перпендикуляров, проведённых ко всем сторонам данного треугольника.

  

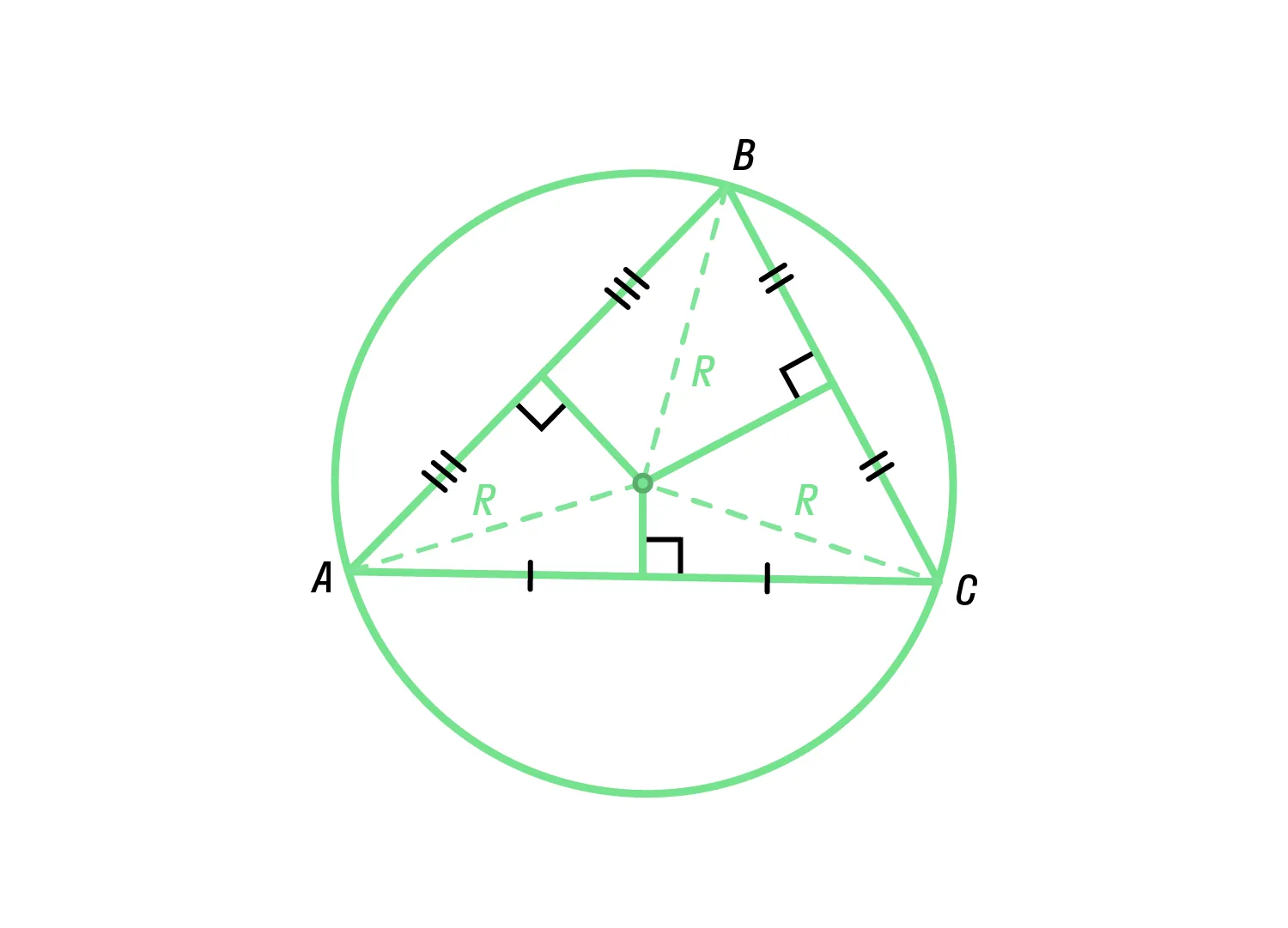
• Центр окружности, описанной около остроугольного треугольника, лежит внутри треугольника, около прямоугольного треугольника — лежит на середине его гипотенузы, около тупоугольного треугольника — лежит вне треугольника.

  

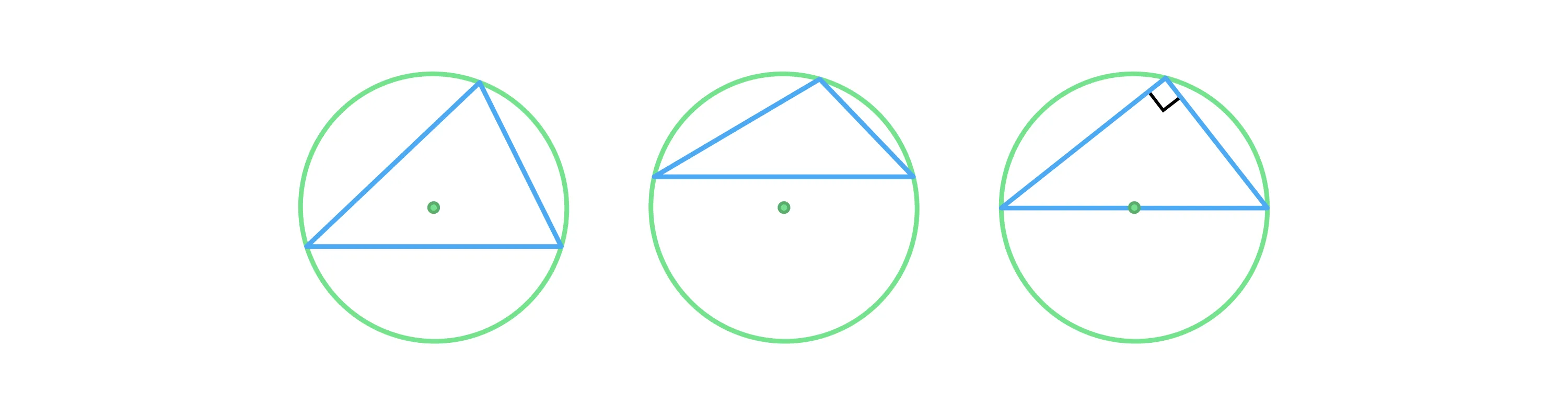
• Радиус окружности, описанной около произвольного треугольника, вычисляется по формуле:
  , где a, b, c — стороны треугольника, S — площадь треугольника.

• Для равностороннего треугольника:
  .

• Для прямоугольного треугольника : , где с — гипотенуза.

• Радиус окружности, описанной около прямоугольного треугольника, равен медиане, проведённой к гипотенузе.

  

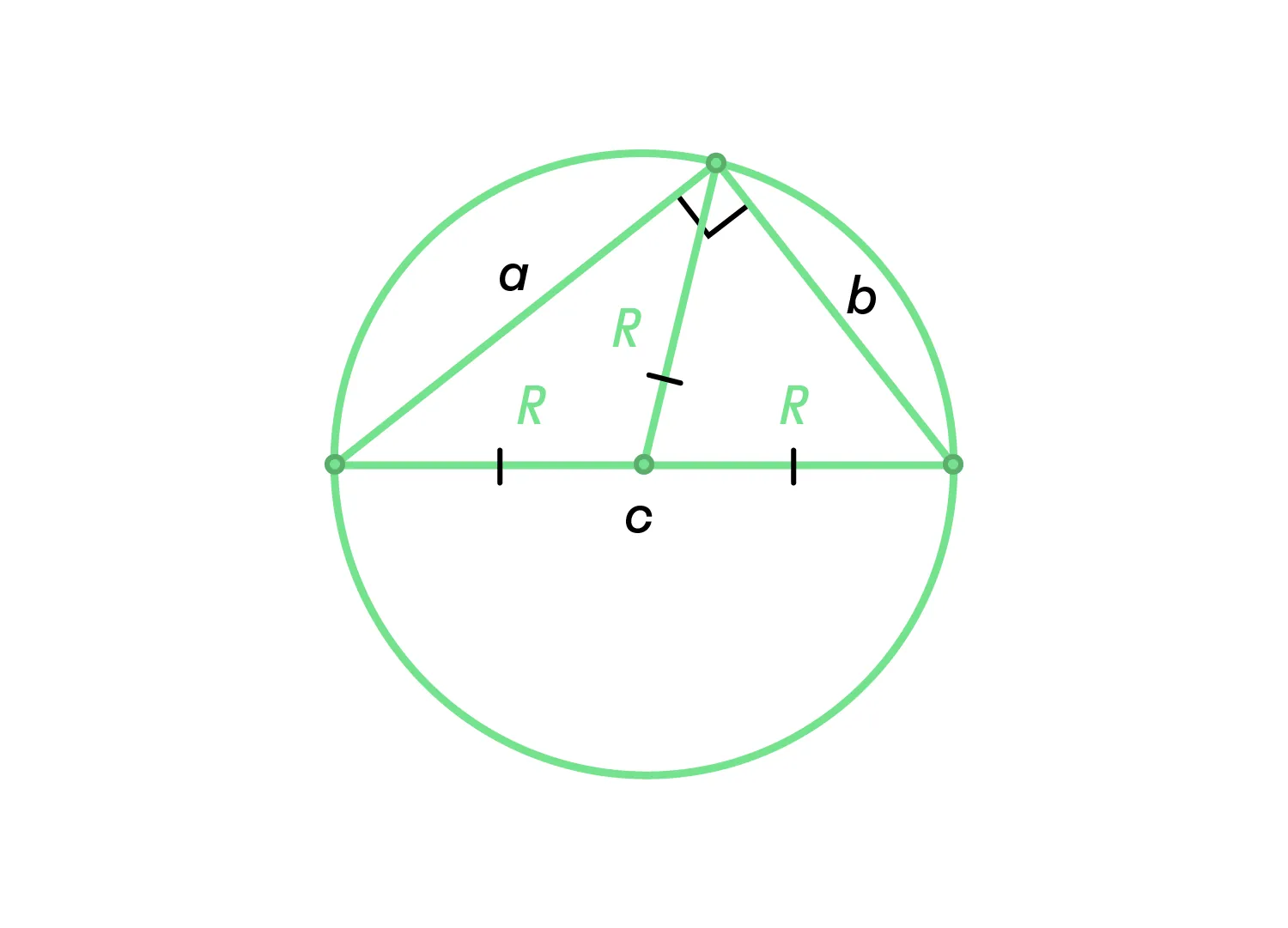
• Теорема синусов и радиус описанной окружности:

  

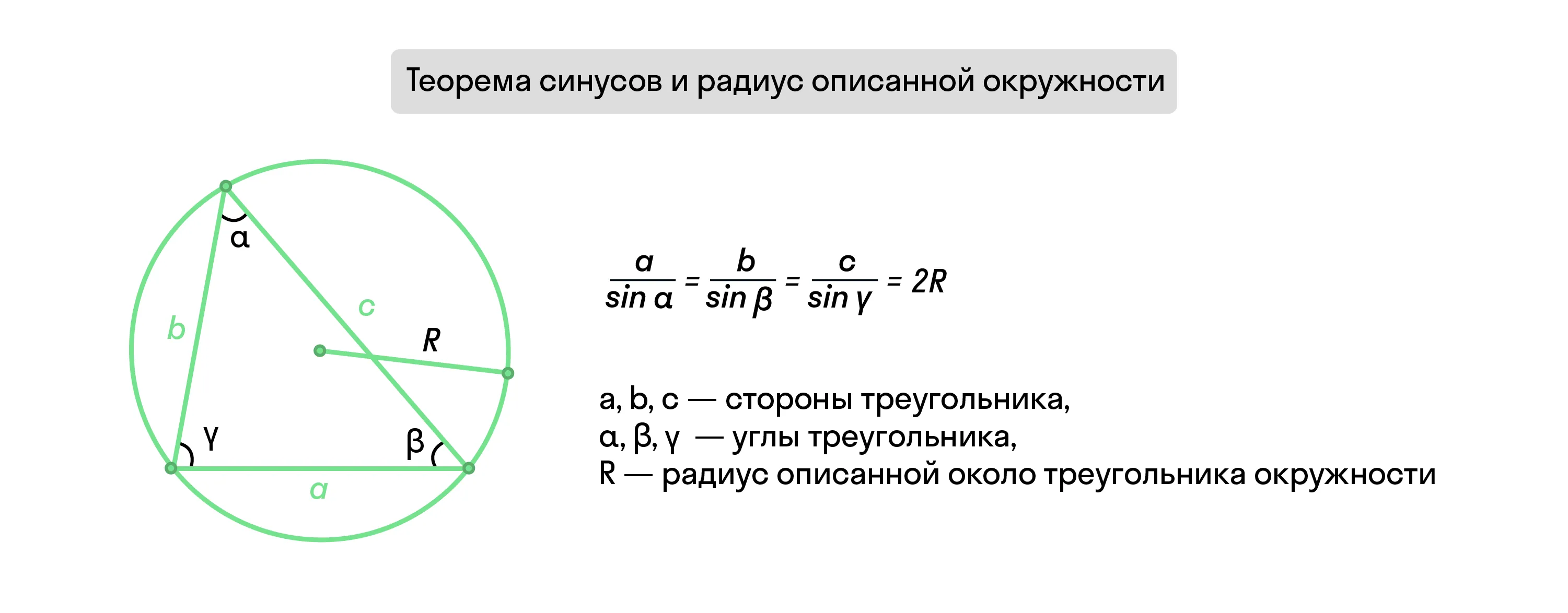
Описанная окружность и четырёхугольник

• Если четырёхугольник описан, то суммы противолежащих углов равны 180° окружность можно описать около прямоугольника, квадрата и равнобедренной трапеции (или другого четырёхугольника, соответствующего свойствам).

• Теорема Птолемея: сумма произведений противолежащих сторон вписанного четырёхугольника ABCD равна произведению диагоналей.

  

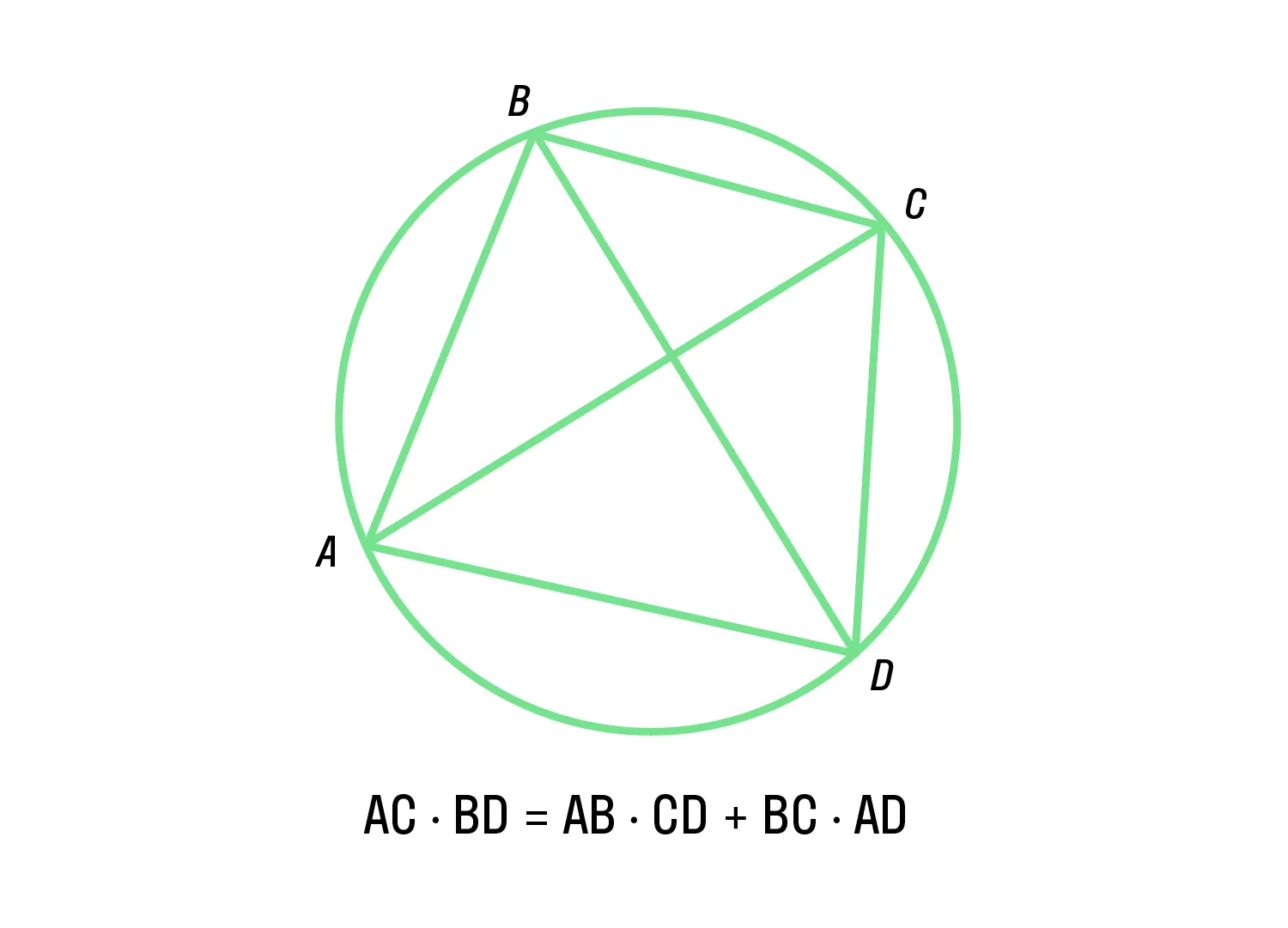
• Диагонали вписанного четырёхугольника разбивают его на две пары подобных треугольников.

• Радиус окружности, описанной около квадрата, можно найти через его диагональ:
  , где d — диагональ квадрата.

Описанная окружность и n-угольник

• Радиус окружности, описанной около правильного многоугольника, рассчитывается по формуле , где n — количество сторон n-угольника.

• Площадь вписанного правильного многоугольника:
  или , где R — радиус описанной окружности, р — полупериметр многоугольника.

• Радиус описанной окружности, проведённый к вершине шестиугольника, — это биссектриса, то есть он делит угол правильного шестиугольника пополам.

Теория — серебро, а вот практика — настоящее золото. Особенно в нашем бесплатном тренажере для подготовки к ОГЭ, ЕГЭ и контрольным работам. Переходите по ссылкам и отрабатывайте полученные знания по темам «Вписанная окружность» и «Описанная окружность»!