Арифметическая прогрессия: свойства и формулы

Определение числовой последовательности

Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер.

Последовательности можно задавать разными способами:

 

1. Словесно — когда правило последовательности объясняется словами:

   «Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23...»



2. Аналитически — когда указана формула ее n-го члена: y_n = f(n).

   Последовательность y_n = C называют постоянной или стационарной.



3. Рекуррентно — когда указывается правило, которое помогает вычислить n-й член последовательности, если известны её предыдущие члены.

   Последовательность Фибоначчи — когда каждое следующее число равно сумме двух предыдущих чисел: a_n+1 = a_n + a_n-1.

   Пример: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55...



4. Графически — когда график последовательности состоит из точек с абсциссами
   1, 2, 3, 4...
   

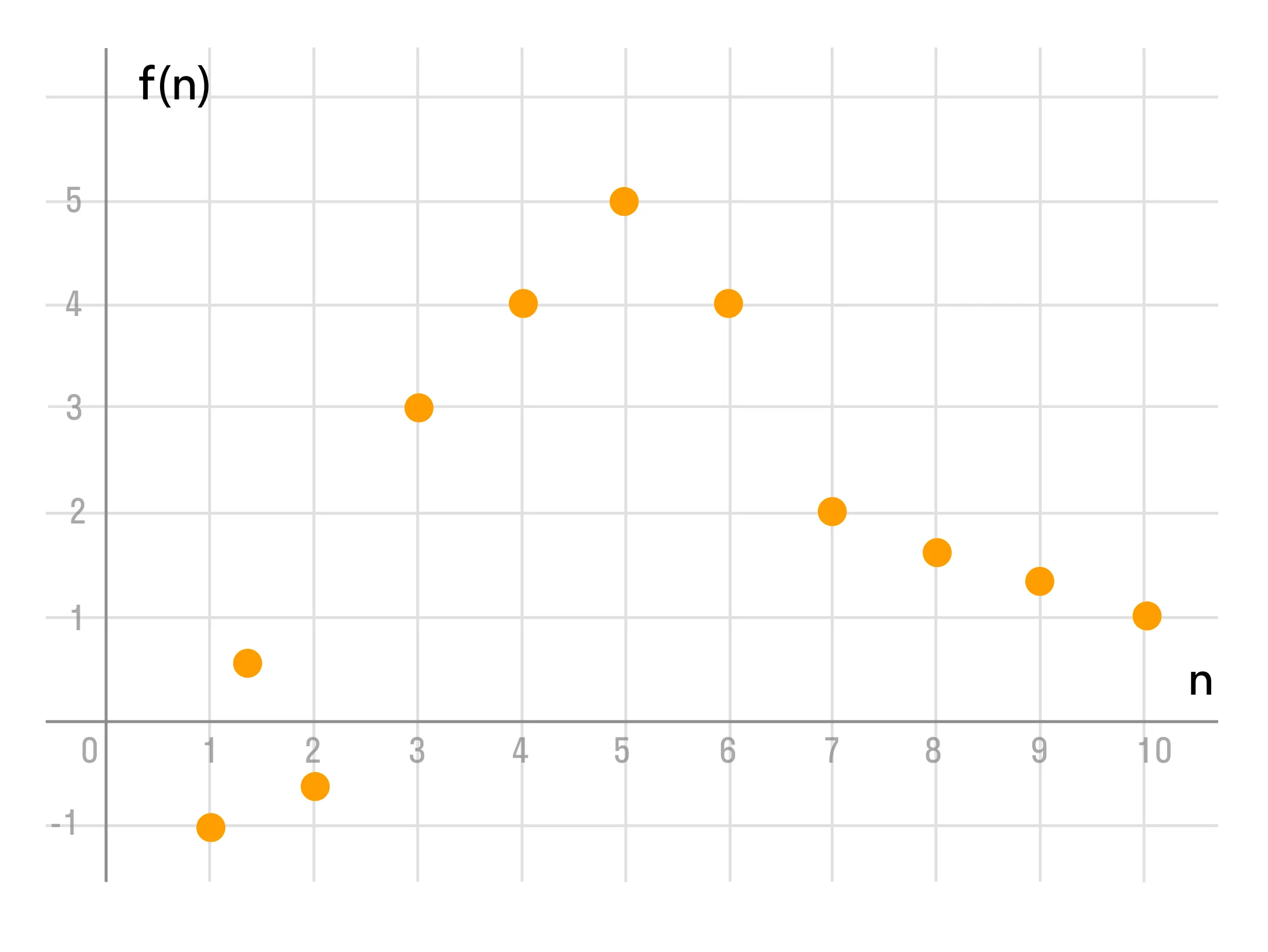
Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей.

Свойства числовых последовательностей:

 

1. Последовательность {y_n} называют возрастающей, если каждый ее член кроме первого больше предыдущего:

   y₁ < y₂ < y₃ < … < y_n < y_n+1 < …



2. Последовательность {y_n} называют убывающей, если каждый ее член кроме первого меньше предыдущего:

   y₁ > y₂ > y₃ > … > y_n > y_n+1 > …

   Возрастающие и убывающие последовательности называют монотонными последовательностями.



3. Последовательность можно назвать периодической, если существует такое натуральное число T, что начиная с некоторого N, выполняется равенство: y_n = y_n+T. Число T — длина периода.

 

 

Запишем числа, которые первые пришли в голову: 7, 19, 0, −1, −2, −11, 0… Сколько бы чисел не написали, всегда можно сказать, какое из них первое, какое — второе и так до последнего. То есть мы можем их пронумеровать.

Пример числовой последовательности выглядит так:

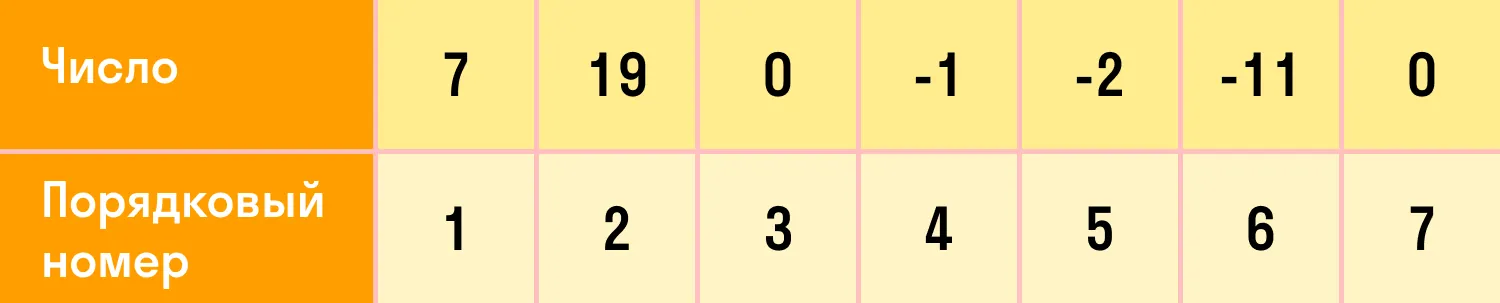
В такой математической последовательности каждый номер соответствует одному числу. Это значит, что в последовательности не может быть двух первых чисел и т.д. Первое число (как и любое другое) — всегда одно.

N-ный член алгебраической последовательности — это число с порядковым номером n.

Всю последовательность можно обозначить любой буквой латинского алфавита, например, a. Каждый член этой последовательности — той же буквой с индексом, который равен номеру этого члена: a₁, a₂,..., a₁₀..., a_n.

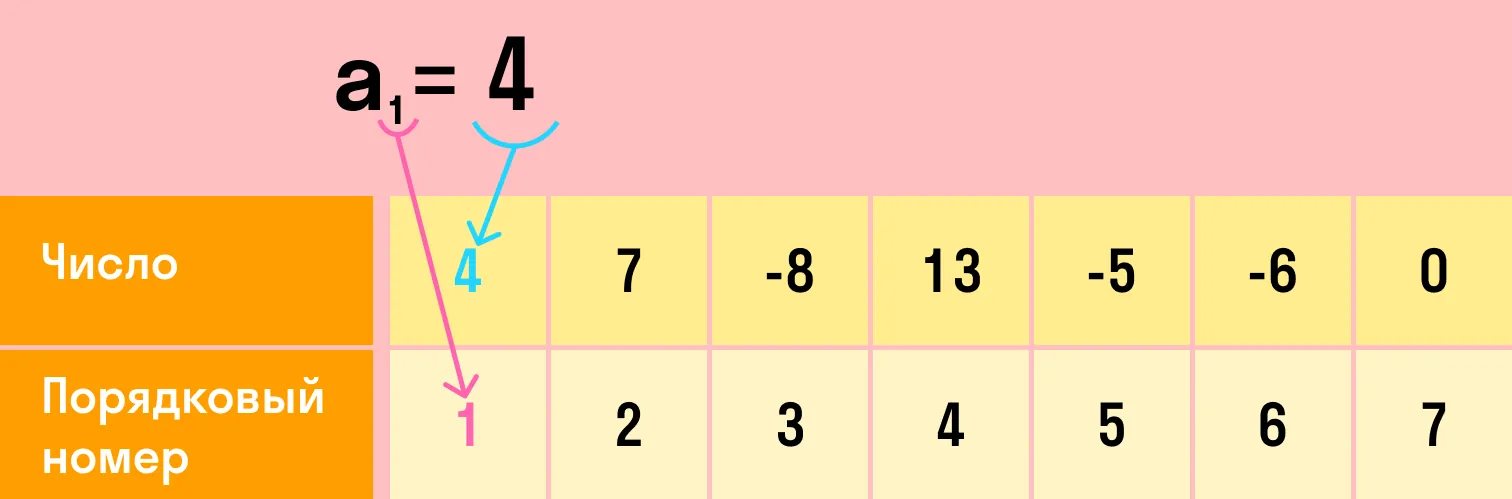
N-ый член последовательности можно задать формулой. Например:

• Формула a_n = 3n − 5 задает последовательность: −2, 1, 4, 7, 10…
• Формула a_n = 1 : (n + 2) задает последовательность: 1/3, 1/4, 1/5, 1/6...

Определение арифметической прогрессии

Так как числовая последовательность — это частный случай функции, которая определена на множестве натуральных чисел, арифметическую прогрессию можно назвать частным случаем числовой последовательности.

Рассмотрим основные определения и как найти арифметическую прогрессию.

Арифметическая прогрессия — это числовая последовательность a1, a2,..., an,... для которой для каждого натурального n выполняется равенство: an+1= an + d, где d — это разность арифметической прогрессии.

Описать словами эту формулу можно так: каждый член арифметической прогрессии равен предыдущему, сложенному с одним и тем же числом d.

Разность между последующим и предыдущим членами, то есть разность арифметической прогрессии можно найти по формуле:

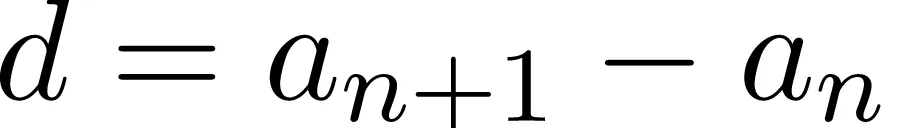
Если известны первый член a₁ и n-ый член прогрессии, разность можно найти так:

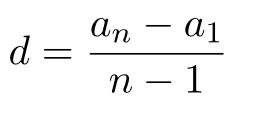
Арифметическая прогрессия бывает трех видов:

 

1. Возрастающая — арифметическая прогрессия, у которой положительная разность, то есть d > 0.

   Пример: последовательность чисел 11, 14, 17, 20, 23... — это возрастающая арифметическая прогрессия, так как ее разность d = 3 > 0.



2. Убывающая — арифметическая прогрессия, у которой отрицательная разность, то есть d < 0.

   Пример: последовательность чисел 50, 48, 46, 44, 42... — это убывающая арифметическая прогрессия, так как ее разность d = –2 < 0.



3. Стационарная — арифметическая прогрессия, у которой разность равна нулю, то есть d = 0.

   Пример: последовательность чисел 23, 23, 23, 23, 23... — это стационарная арифметическая прогрессия, так как ее разность d = 0.

Экзамены — это почти всегда стресс. Подготовка к ЕГЭ по математике онлайн в школе Skysmart поможет снять волнение перед экзаменом и придаст уверенности в своих знаниях.

170.4K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Свойство арифметической прогрессии

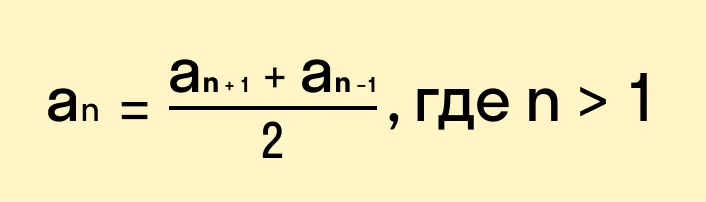
Переведем с языка формул на русский: каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов. Что как раз объясняет название «арифметическая» прогрессия.

Формула n-го члена арифметической прогрессии

Из определения арифметической прогрессии следует, что равенство истинно:

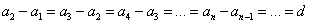
Поэтому:

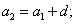
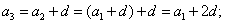
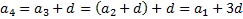
и т.д.

Значит,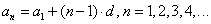

Переведем с языка формул на русский: если мы знаем первый член и разность арифметической прогрессии, то можем найти любой ее член.

Арифметическую прогрессию можно назвать заданной, если известен ее первый член и разность.

Формулу a_n = a₁ + d * (n - 1) называют формулой n-го члена арифметической прогрессии.

Формулы арифметической прогрессии

В 9 классе проходят все формулы арифметической прогрессии. Давайте узнаем, какими способами ее можно задать:

 

1. Рекуррентной формулой:


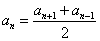
2. Формулой n-го члена: a_n = a₁+ d · (n - 1).


3. Формулой вида a_n = kn + b, где k и b — числа, n — число членов последовательности.

Сумма первых n членов арифметической прогрессии (а_n) обозначается S_n:

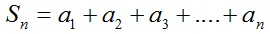
Формулы нахождения суммы n членов арифметической прогрессии:

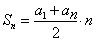
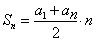
Чтобы быстрее запомнить формулы можно использовать такую табличку с основными определениями:

Рассмотрим пример арифметической прогрессии.

Дано: арифметическая прогрессия (a_n), где a₁ = 0 и d = 2.

Найти: первые пять членов прогрессии и десятый член прогрессии.

Решение арифметической прогрессии:

 

1. Чтобы найти последующий член прогрессии, нужно к предыдущему прибавить разность:

   a₂ = a₁ + d = 0 + 2 = 2;

   a₃ = a₂ + d = 2 + 2 = 4;

   a₄ = a₃ + d = 4 + 2 = 6;

   a₅ = a₄ + d = 6 + 2 = 8.



2. Используем общую формулу a_n = a₁ + d * (n - 1).

   По условиям задачи n = 10, подставляем в формулу:

   a₁₀ = a₁ + 2 * (10 - 1) = 0 + 2⋅9 = 18.

Геометрическая прогрессия

Геометрическая прогрессия — это последовательность (b_n), в которой каждый последующий член можно найти, если предыдущий член умножить на одно и то же число q.

Если последовательность (b_n) является геометрической прогрессией, то для любого натурального значения n справедлива зависимость:

bn+1 = bn * q, где q — знаменатель геометрической прогрессии

Если в геометрической прогрессии (b_n) известен первый член b₁ и знаменатель q, то можно найти любой член прогрессии:

• b₂ = b₁ * q;
• b₃ = b₂ * q = b₁ * q * q = b₁ * q²;
• b₄ = b₁ * q³;
• и т. д.

Общий член геометрической прогрессии bn можно вычислить при помощи формулы:

b_n = b₁ * qⁿ⁻¹, где n — порядковый номер члена прогрессии, b₁ — первый член прогрессии, q — знаменатель.

Пример 1. 2, 6, 18, 54,… — геометрическая прогрессия b = 2, q = 3.

Пример 2. 3, -3, 3, -3,… — геометрическая прогрессия b = 3, q = -1.

Пример 3. 7, 7, 7, 7,… — геометрическая прогрессия b = 7, q = 1.