Треугольник: определение и типы
Треугольник — геометрическая фигура, которая состоит из трёх сторон и трёх вершин.
Вершины треугольника принято обозначать заглавными буквами латинского алфавита. Стороны треугольника можно обозначить через названия двух вершин, точки которых являются началом и концом отрезка (стороны). Если же вершины не обозначены, стороны можно записать через малые буквы латинского алфавита.
Треугольники бывают трёх видов:
-
Остроугольные (все углы, входящие в состав, острые).
-
Прямоугольные (один угол прямой, равен 90°, остальные острые).
-
Тупоугольные (один угол тупой, остальные острые).
Также выделяют равнобедренные и равносторонние треугольники.
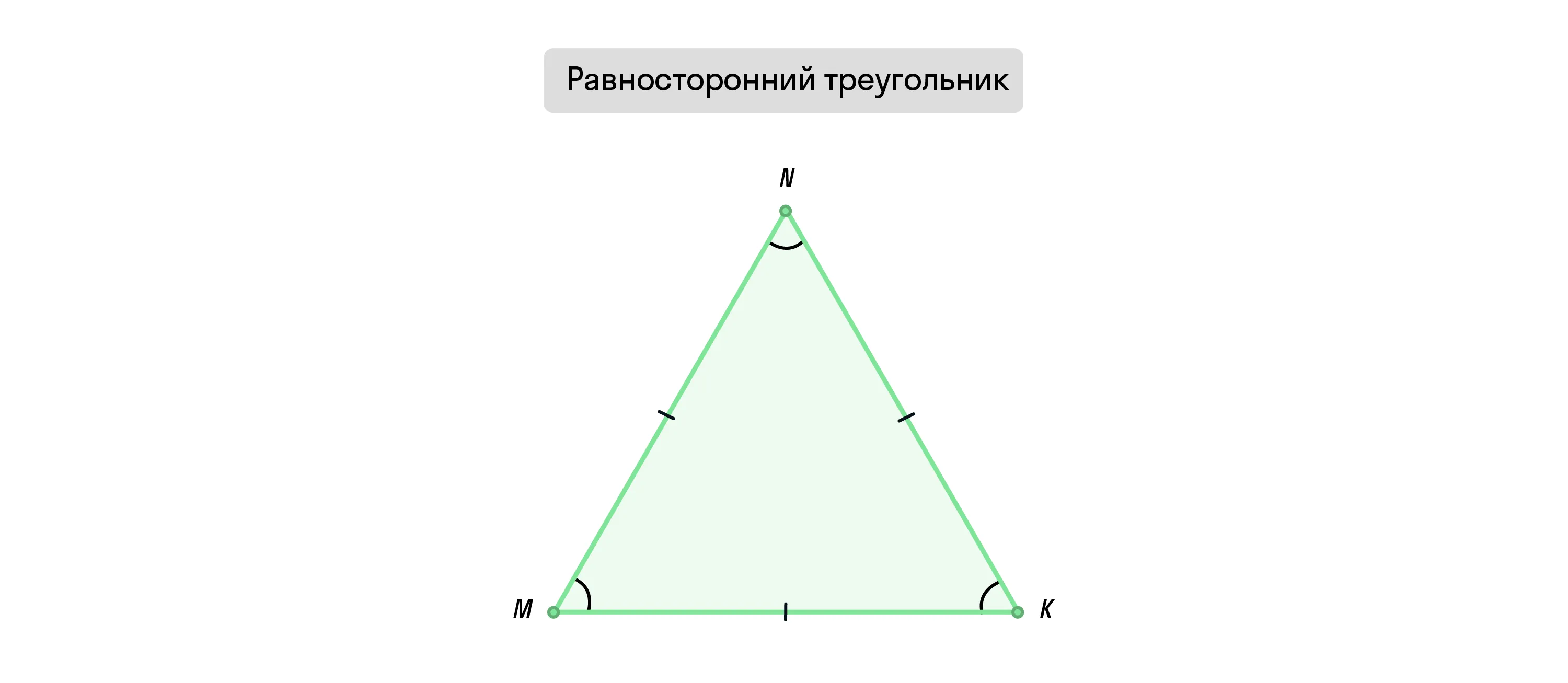
Равносторонний треугольник — треугольник, все стороны и углы которого равны.
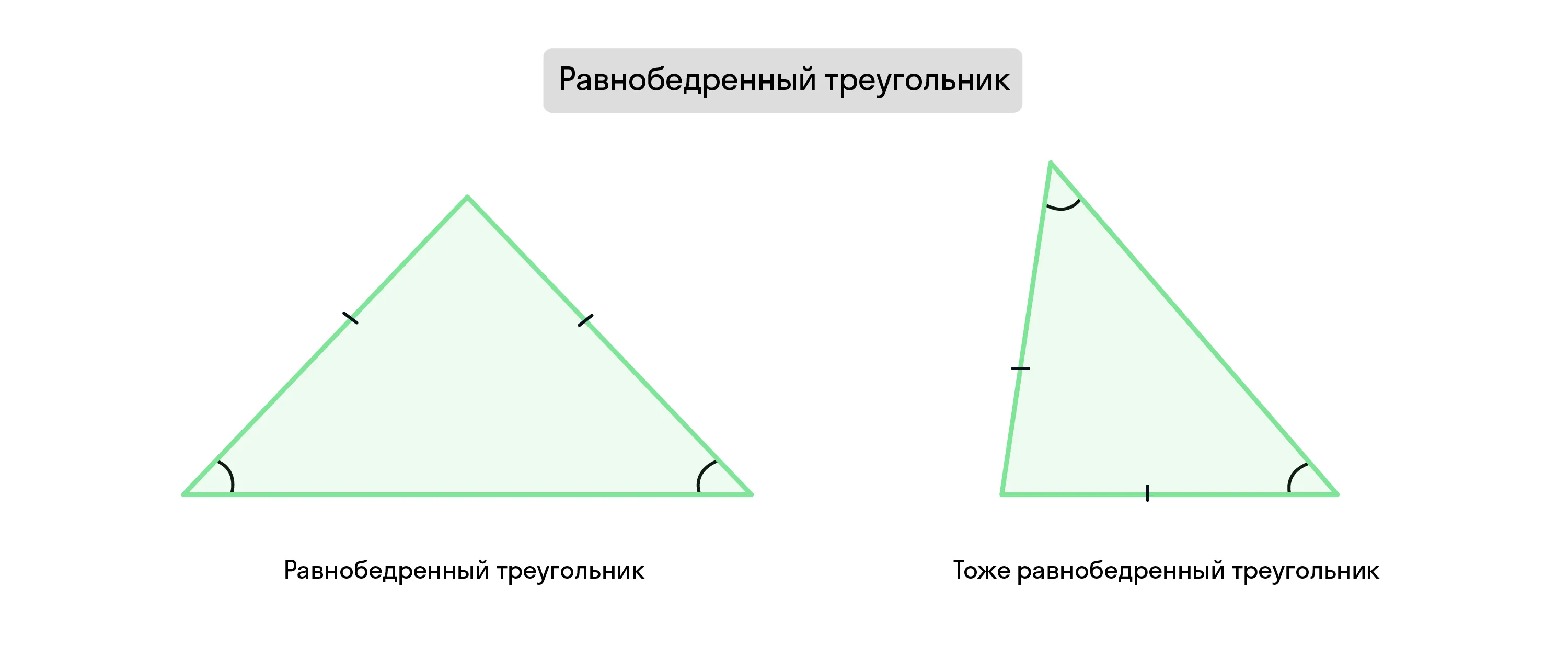
Равнобедренный треугольник — треугольник, у которого равны боковые стороны и углы при основании.
Зачастую в учебниках и справочных материалах равнобедренные треугольники рисуют таким образом, что равные боковые стороны располагаются слева и справа, основанием считается нижняя сторона. Но вы должны понимать, что равнобедренный треугольник можно легко перевернуть, при этом он не поменяет своих свойств. Именно поэтому определение лучше запомнить так:
Равнобедренный треугольник — треугольник, у которого равны две стороны и углы, противолежащие этим сторонам.
Равнобедренный треугольник: свойства, признаки и формулы
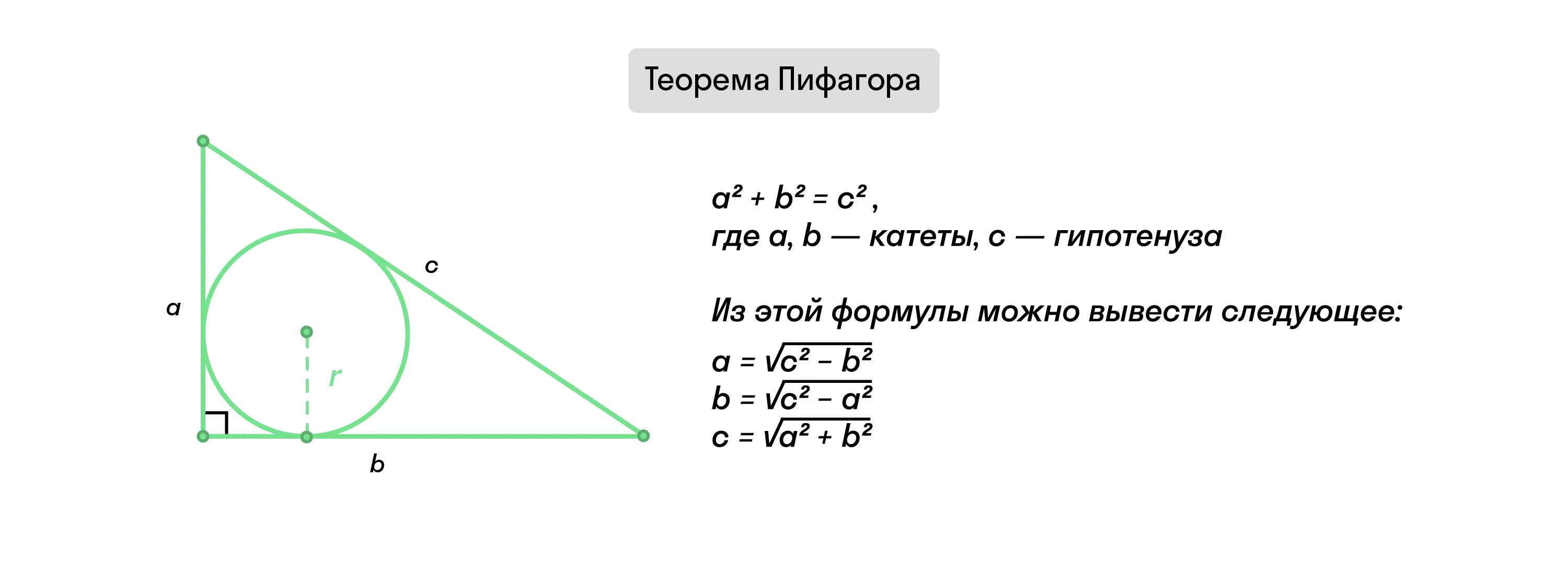
Прямоугольный треугольник и теорема Пифагора
Стороны в прямоугольном треугольнике называются по-особенному. Так, сторона, лежащая напротив прямого угла, называется гипотенузой, она самая большая. Две другие стороны — катеты. Между ними существует соотношение, именуемое теоремой Пифагора.
Важные свойства:
-
катет, лежащий напротив угла 30°, равен половине гипотенузы;
-
в равнобедренном прямоугольном треугольнике острые углы равны 45°.
Получи больше пользы от Skysmart:
-
Подготовься к ОГЭ на пятёрку.
-
Подготовься к ЕГЭ на высокие баллы.
Записывайся на бесплатные курсы для детей.
Решай задания в бесплатном тренажёре ЕГЭ.
Медианы треугольника
Медиана — отрезок, проведенный из вершины угла треугольника к противолежащей стороне и делящий эту сторону пополам.
В треугольнике можно провести три медианы, все они будут лежать внутри треугольника и пересекаться в одной точке. Эта точка называется замечательной точкой треугольника, а также является его центром тяжести.
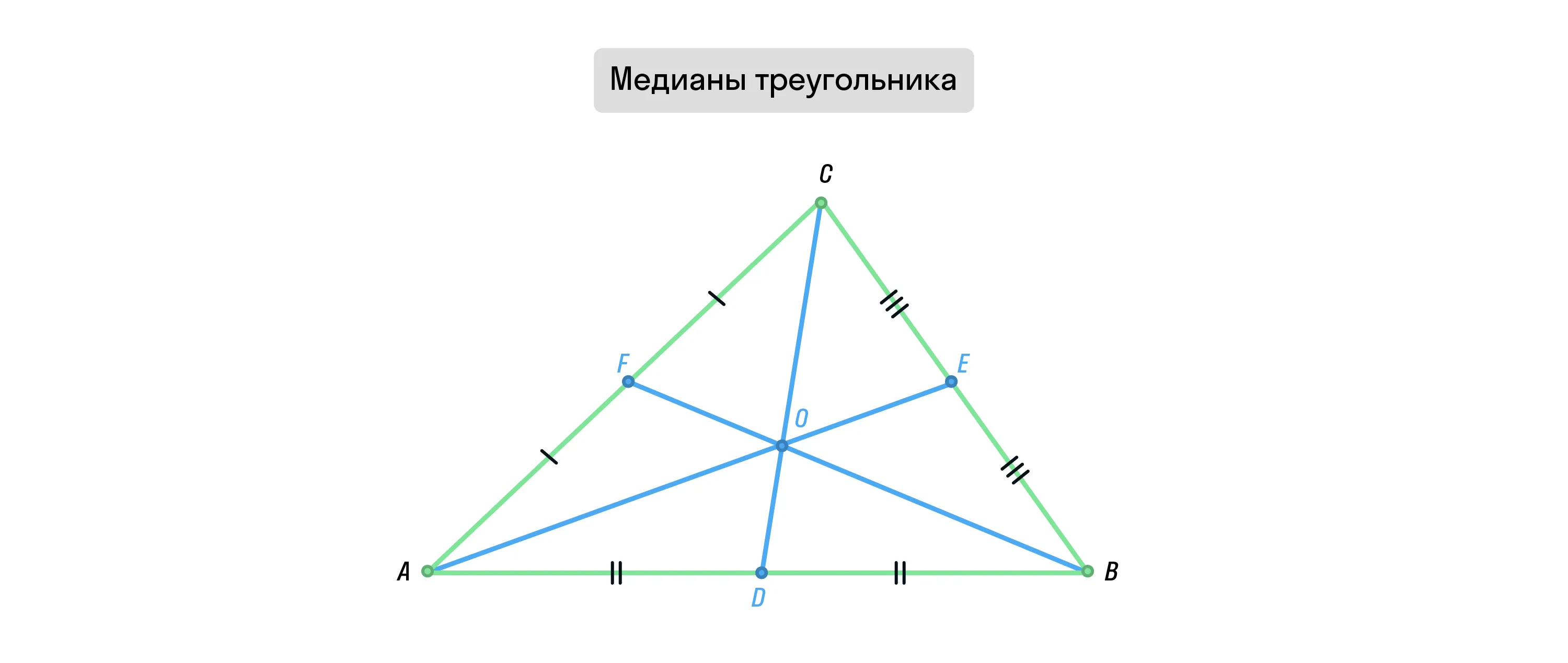
AE, CD, BF — медианы.
Точка О — точка пересечения медиан.
AO : OE = 2 : 1
CO : OD = 2 : 1
BO : OF = 2 : 1
Для решения задач могут понадобиться следующие свойства медиан:
-
В равнобедренном треугольнике медианы, проведённые к равным сторонам, равны, а третья является и биссектрисой, и высотой.
-
В равностороннем треугольнике все медианы равны друг другу.
-
В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна её половине.
-
Медиана разбивает треугольник на два равных по площади (равновеликих) треугольника, а три медианы — на шесть равновеликих треугольников.
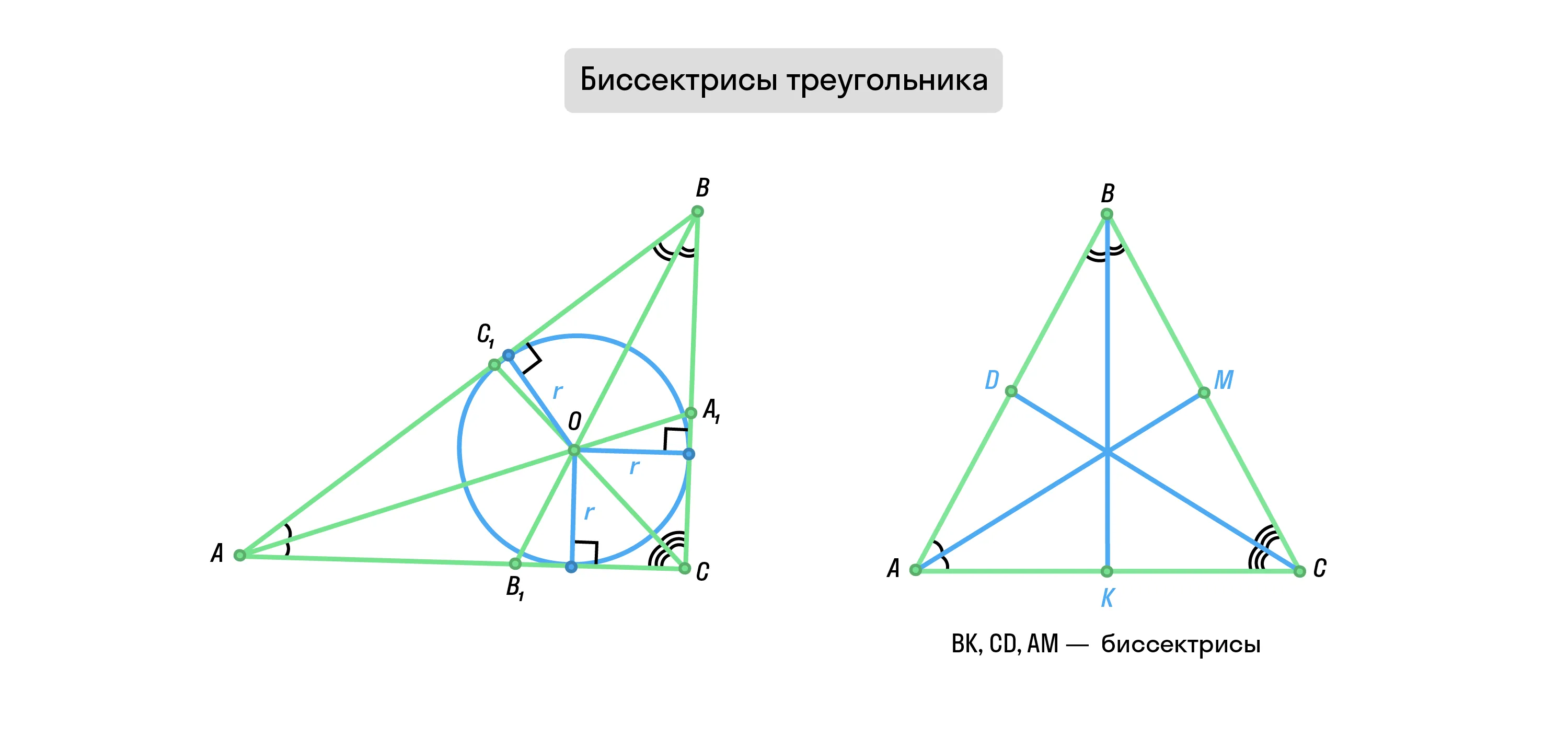
Биссектрисы треугольника
Биссектриса треугольника — отрезок биссектрисы угла, проведенный из вершины его вершины к противолежащей стороне и делящий этот угол пополам.
Биссектрисы углов лежат внутри треугольника и пересекаются в одной точке, которую также называют замечательной. Она является и центром вписанной в треугольник окружности.
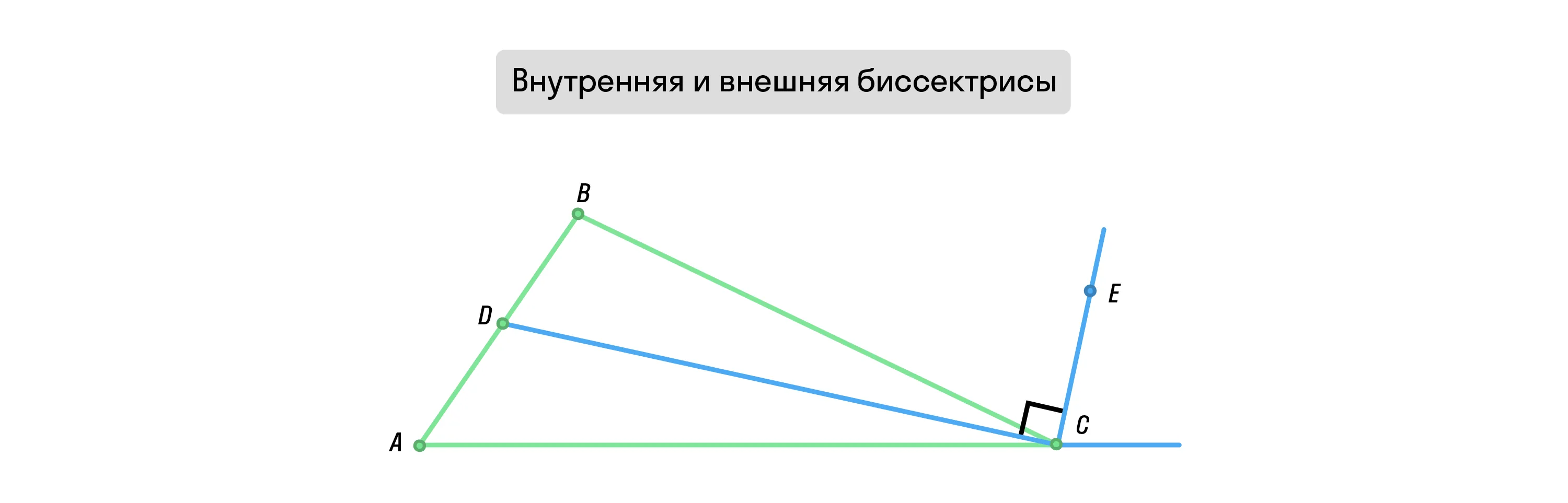
В треугольнике можно провести не только биссектрисы внутренних углов, но и внешних (смежных со внутренними). Внутренняя и внешняя биссектрисы одного и того же угла будут перпендикулярны друг другу.
Дополнительные свойства биссектрис треугольника:
-
Если в треугольнике две биссектрисы равны, то такой треугольник является равнобедренным. При этом третья биссектриса будет является и медианой, и высотой.
-
В равностороннем треугольнике все биссектрисы равны друг другу.
-
Расстояния (кратчайшие расстояния) от сторон угла до любой точки биссектрисы одинаковы.
-
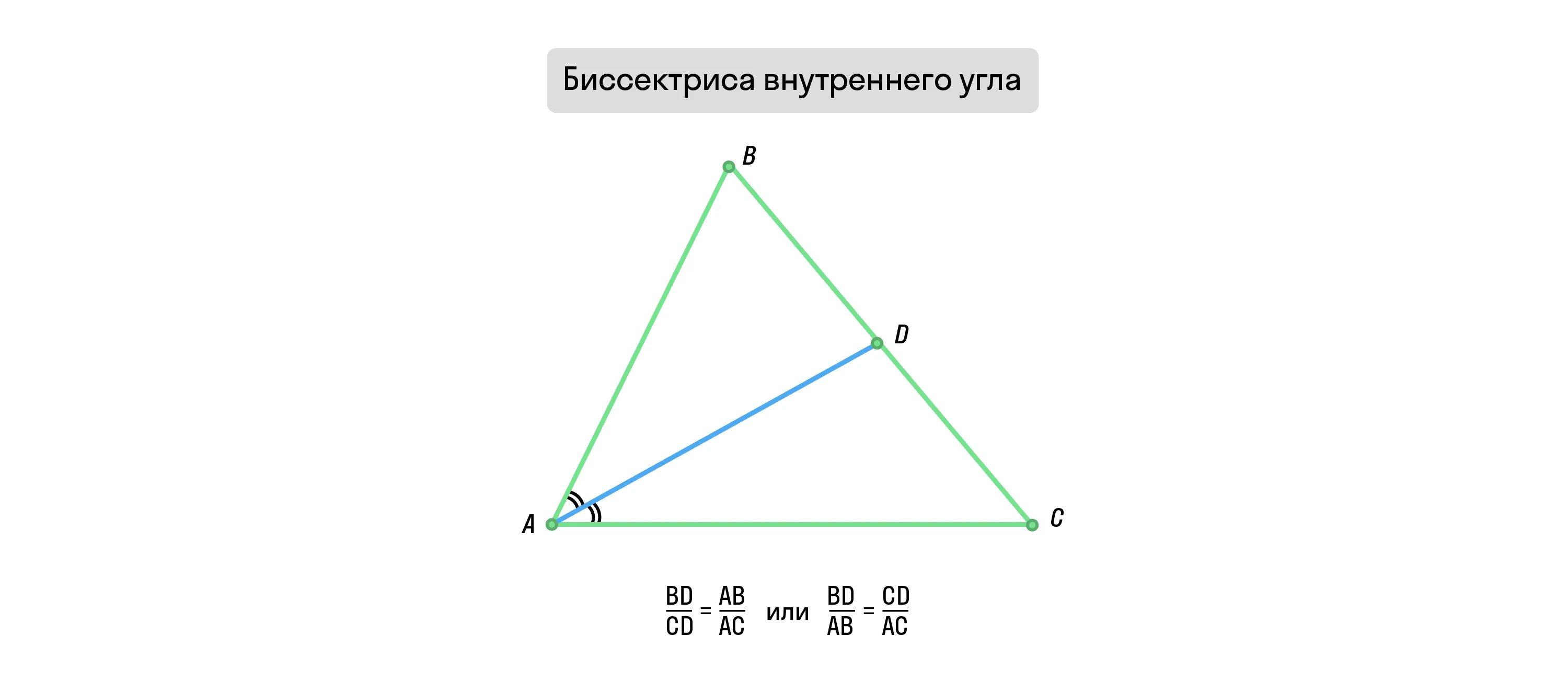
Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон.
А вы знали, что есть не только биссектриса, но и антибиссектриса? Узнать, для чего в геометрии ввели это понятие, вы сможете на уроках математики в школе Skysmart. Записывайтесь на бесплатное вводное занятие и становитесь самым умным в своём классе! 😎
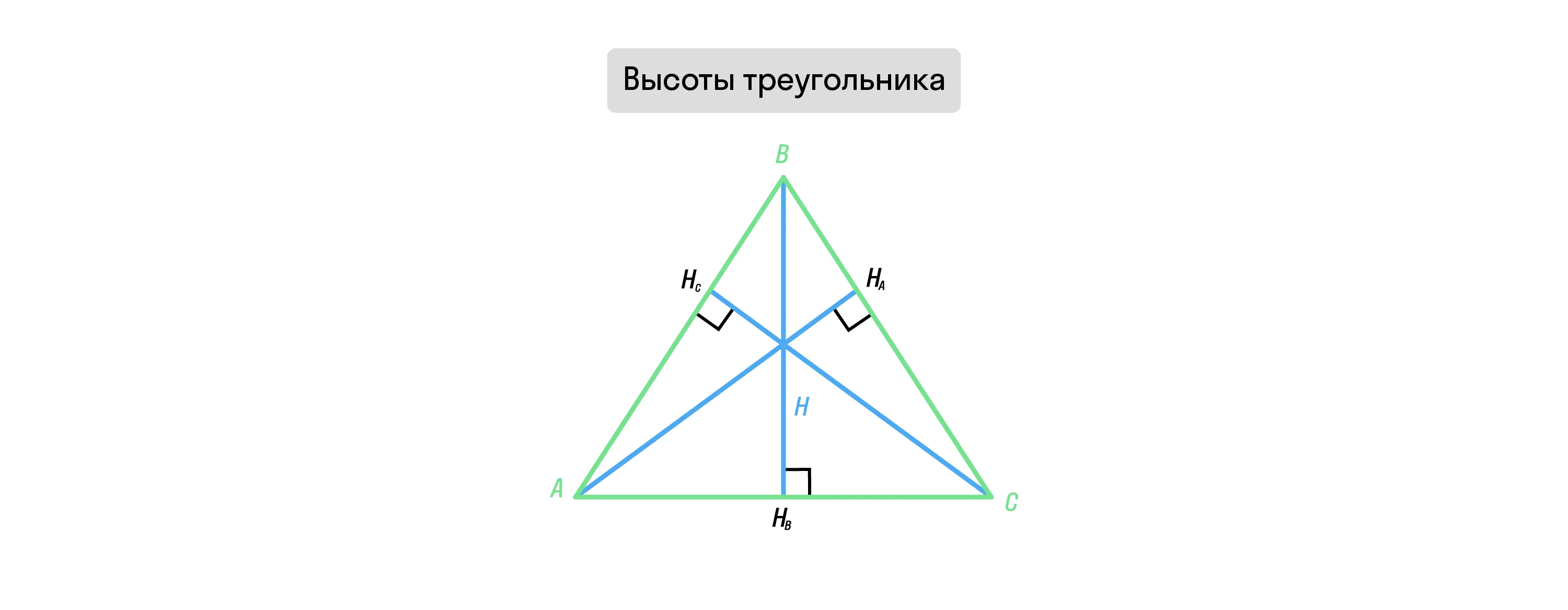
Высоты треугольника
Высота треугольника — перпендикуляр, проведённый из вершины угла к противолежащей стороне (или прямой, содержащей противоположную сторону).
Странное определение, правда? Чуть ниже расскажем, почему оно справедливо.
Чаще всего высоту обозначают буквой h (H).
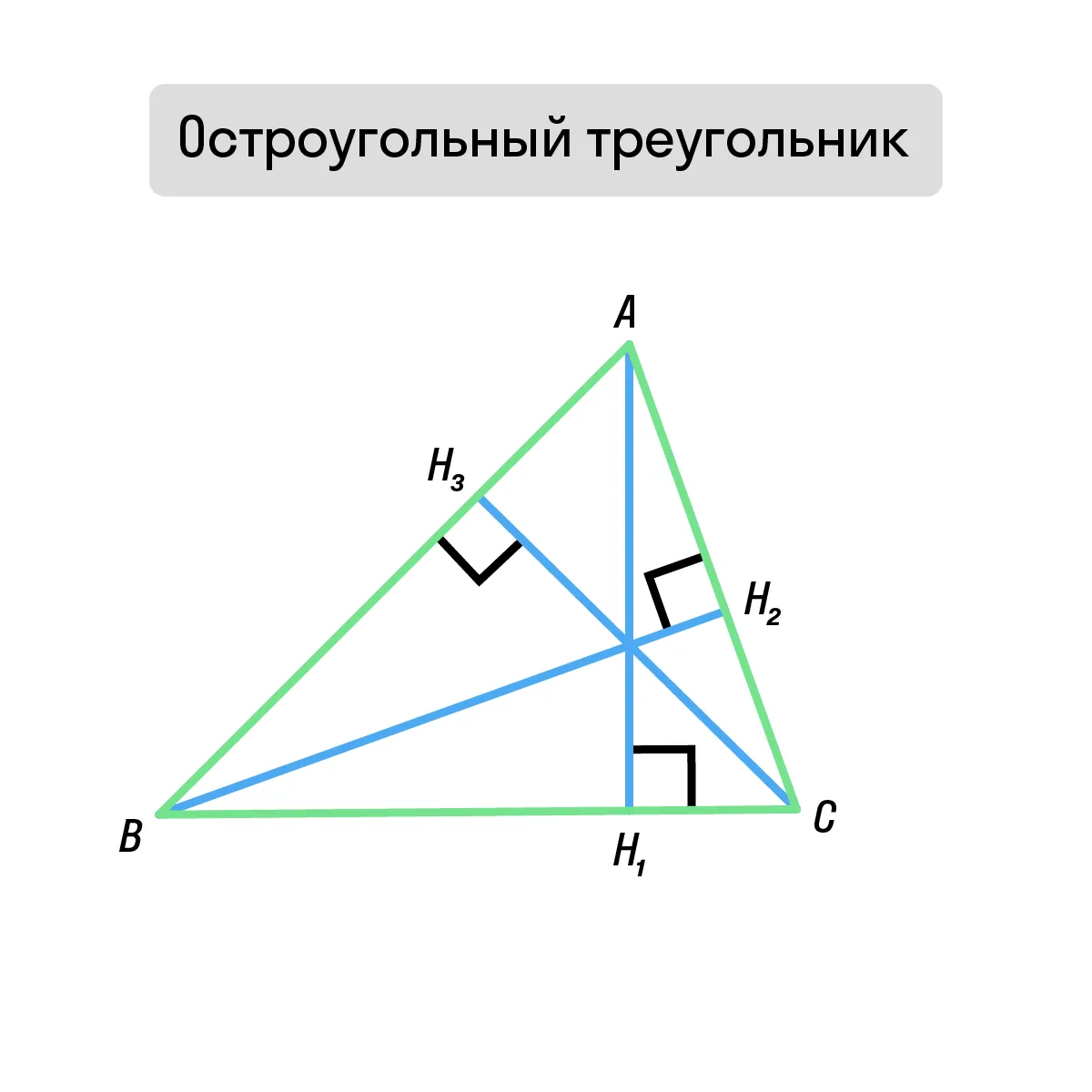
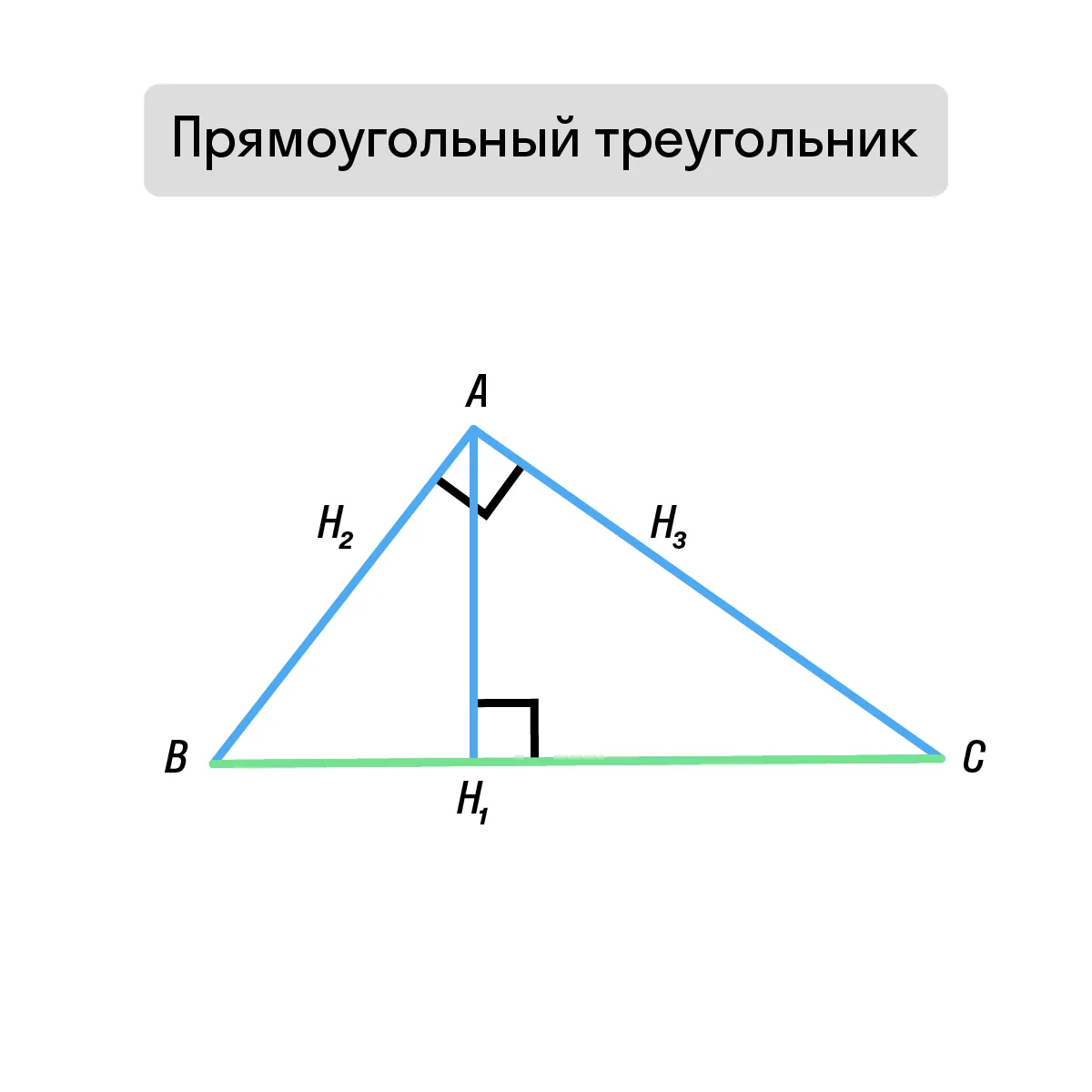
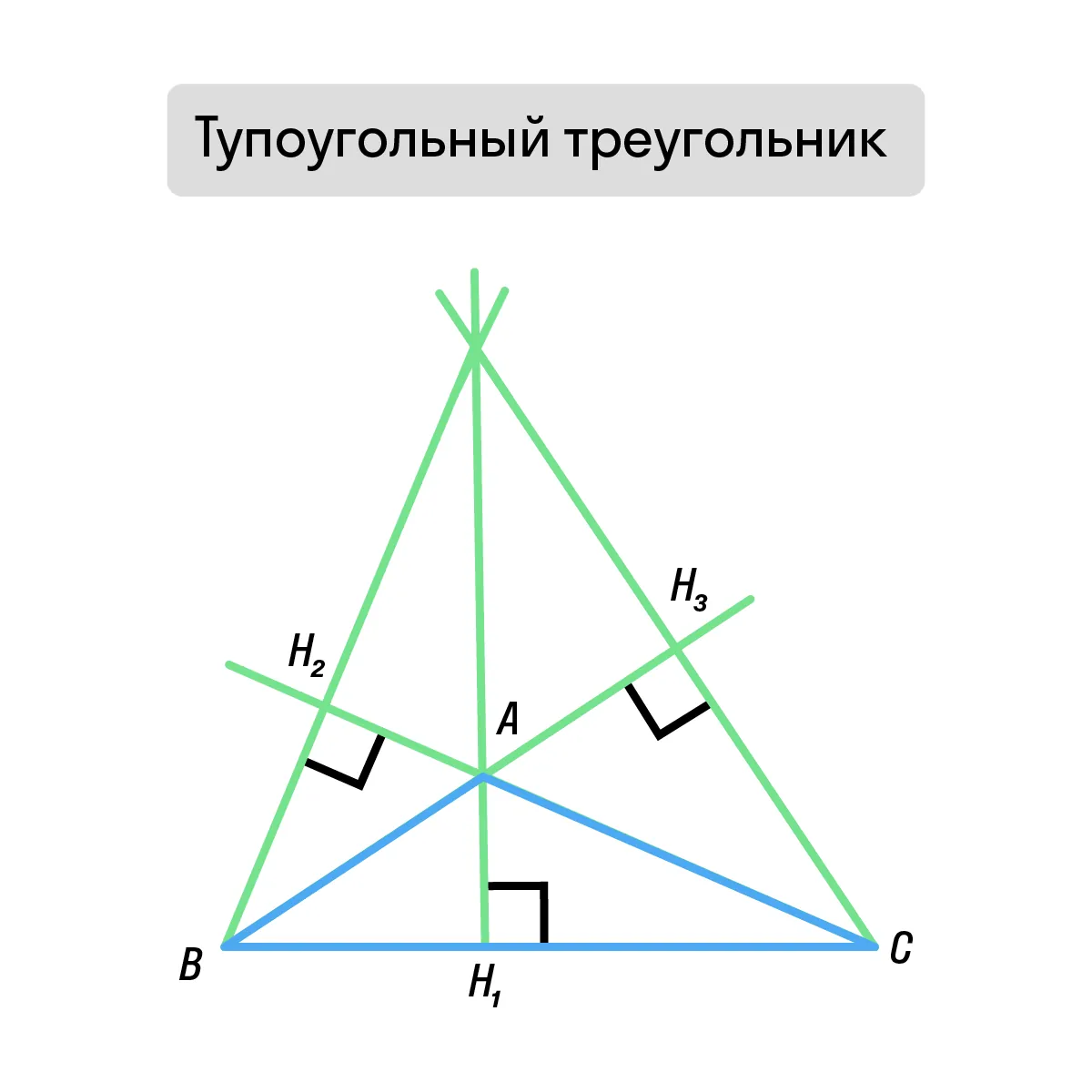
В зависимости от типа треугольника, высоты и точка их пересечения (ортоцентр) могут располагаться по-разному.
|
Остроугольный треугольник Высоты и точка их пересечения находятся внутри треугольника. |
|
|
Прямоугольный треугольник Две высоты совпадают с катетами; точка пересечения находится в вершине прямого угла. |
|
|
Тупоугольный треугольник Две высоты и точка пересечения лежат вне треугольника. |
|
В случае тупоугольного треугольника невозможно провести высоты из вершин острых углов так, чтобы они оставались внутри треугольника. Необходимо продлить боковые стороны и спроецировать высоты именно на продолжение (т. е. на прямую, которая содержит боковую сторону).
Любую высоту треугольника можно найти с помощью формул:
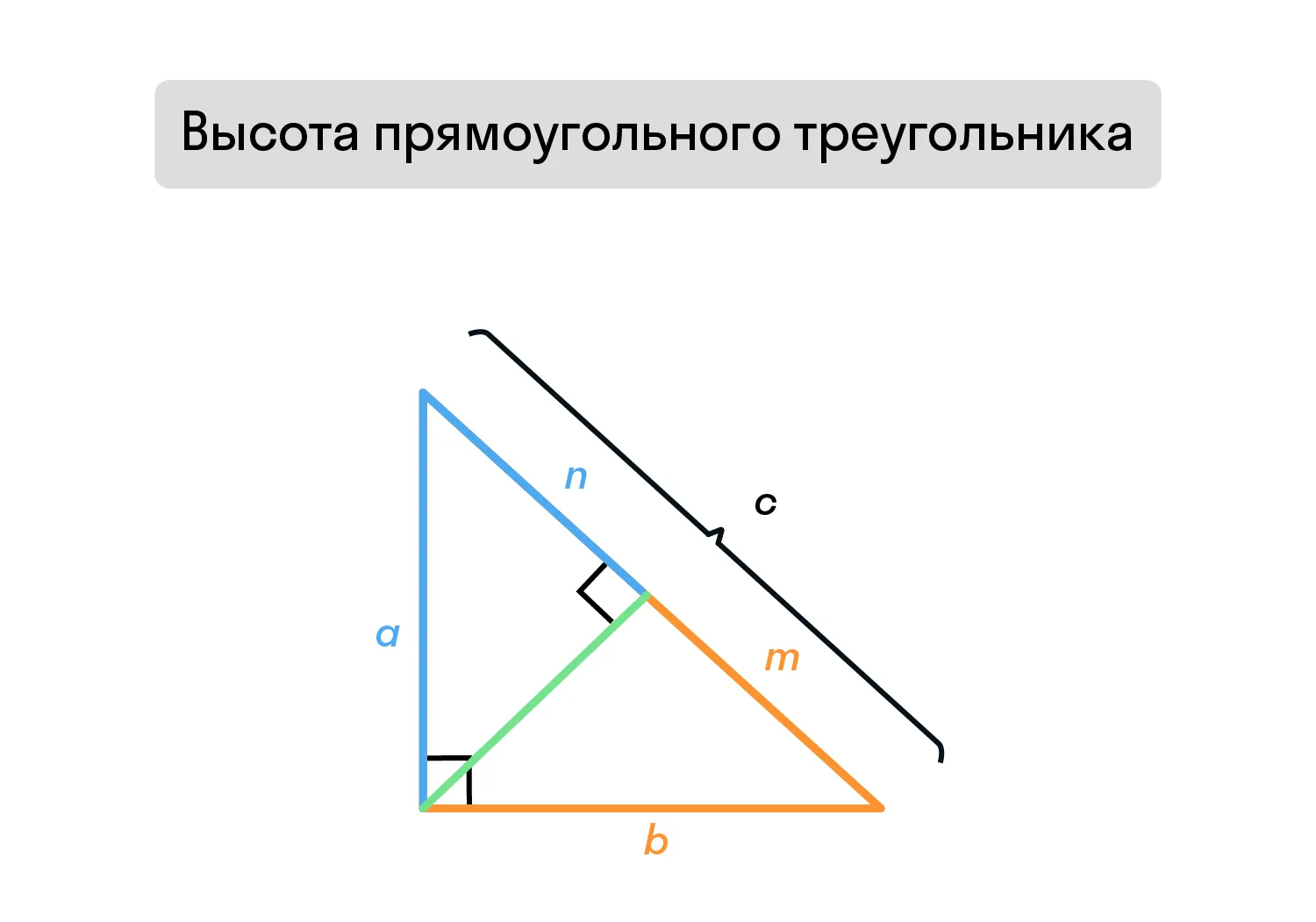
Интересные свойства высот в прямоугольном треугольнике:
-
Высоты, проведённые в прямоугольном треугольнике, связаны соотношением
-
Высота, проведённая из вершины прямого угла, разделит гипотенузу на отрезки m и n. Тогда:
Средняя линия треугольника
Средняя линия треугольника — линия, соединяющая середины двух сторон и параллельная третьей.
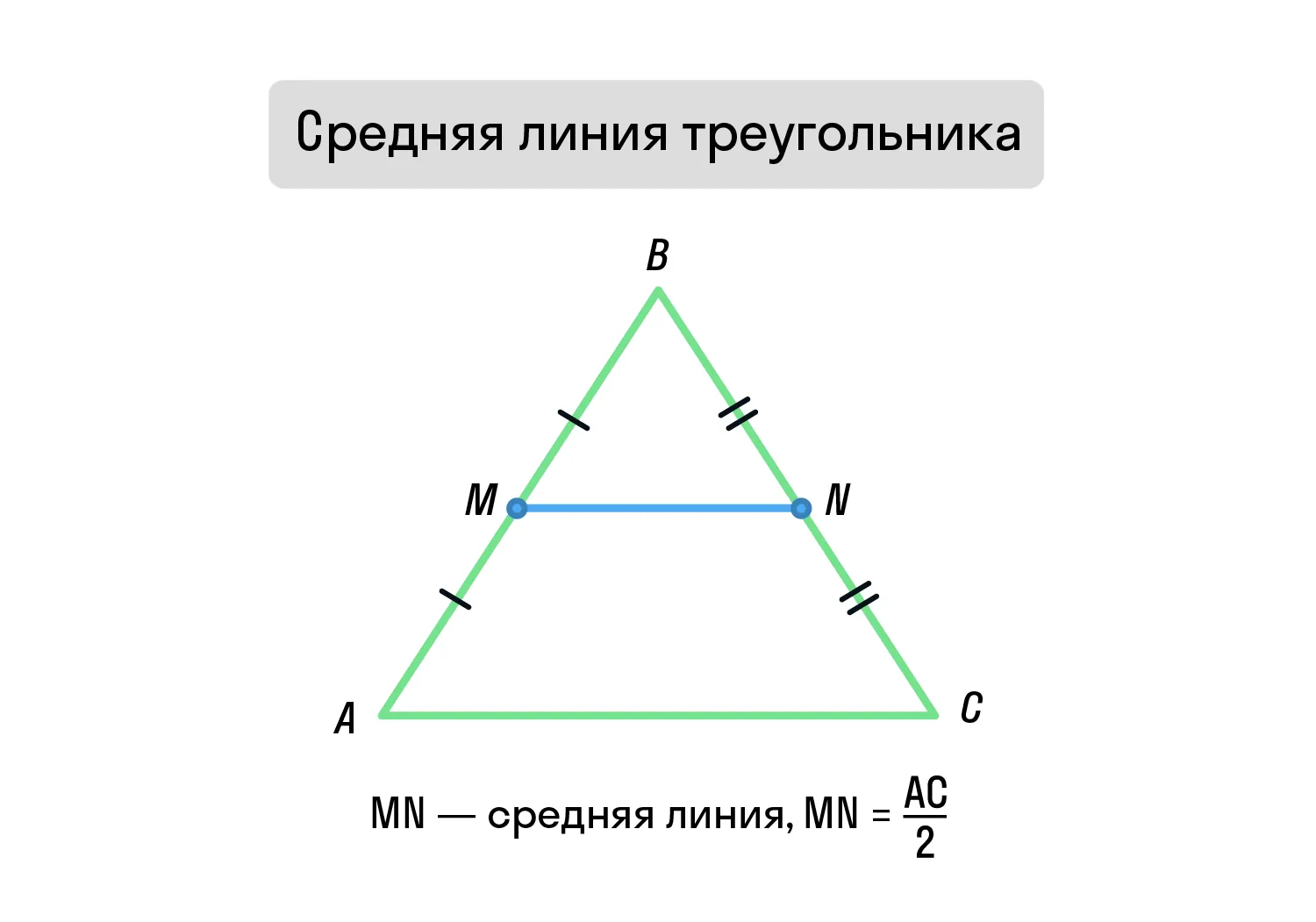
Свойства:
-
Средняя линия равна половине стороны, которой она параллельна.
-
Средняя линия отсекает треугольник, подобный данному. Площадь отсечённого треугольника в 4 раза меньше площади исходного:
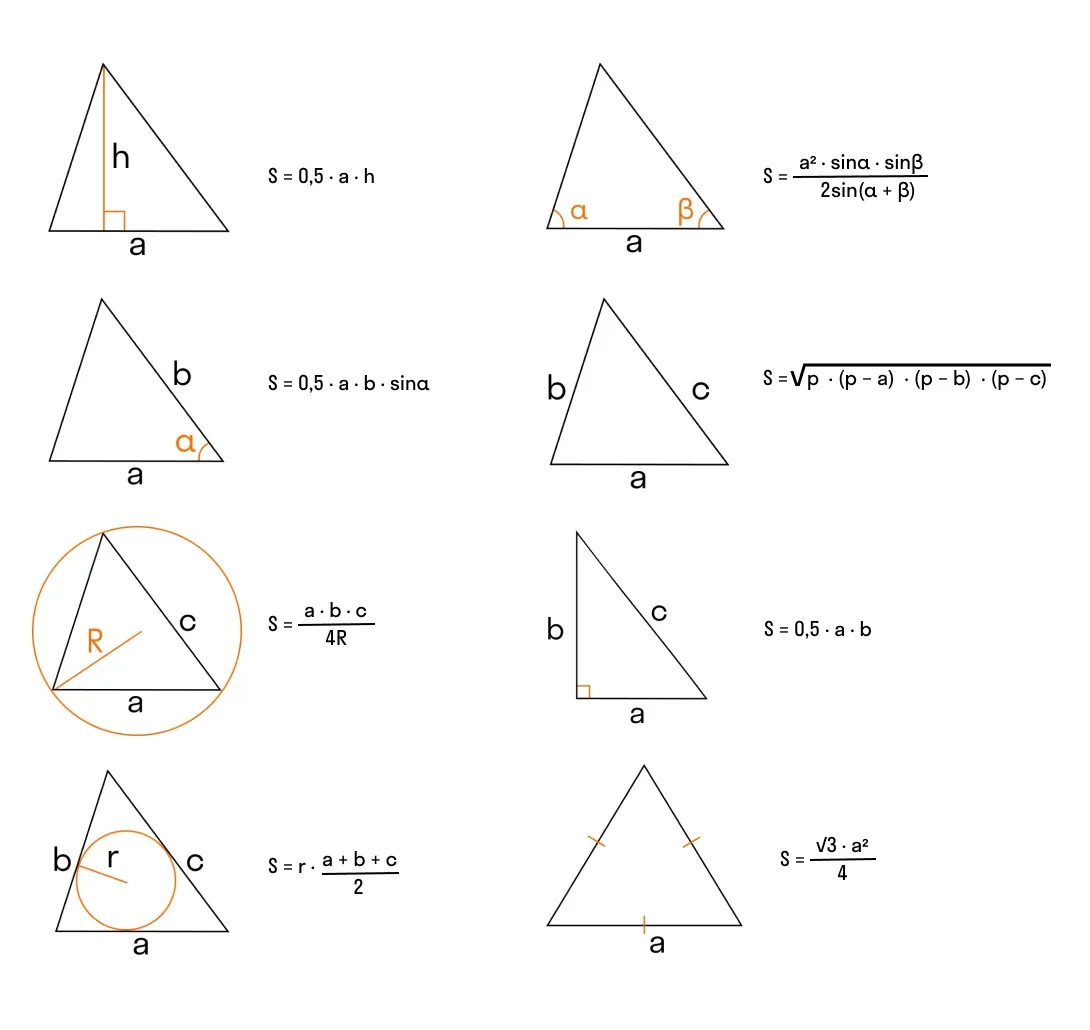
Периметр и площадь треугольника
Периметр треугольника — сумма длин его сторон: P = a + b + c.
Для вычисления площади треугольника используют большое количество формул, вот самые важные — сохраните себе и перешлите друзьям!
Равенство треугольников
Как можно доказать, что треугольники равны? Есть два способа.
Первый — метод наложения. Для этого нам нужно приложить один треугольник к другому таким образом, чтобы совместить их стороны и углы. В случае, если все стороны и углы совпадут (т. е. будут попарно равны), треугольники являются равными друг другу.
Этот метод не очень удобен. Нам необходимо сравнить шесть элементов (три стороны и три угла), что уже немало, и для этого понадобится линейка, транспортир или вырезанные из бумаги треугольники. Столкнувшись со сложностями, математики ещё во времена Древней Греции составили признаки равенства треугольников, которые проще и удобнее использовать для доказательств.
Всего существует 3 универсальных признака равенства треугольников и ещё 4 дополнительных для прямоугольных треугольников. Дополнительные признаки появились из-за того, что стороны прямоугольного треугольника называются иначе, к тому же некоторые из признаков базируются на более сложных постулатах (например, тригонометрии).
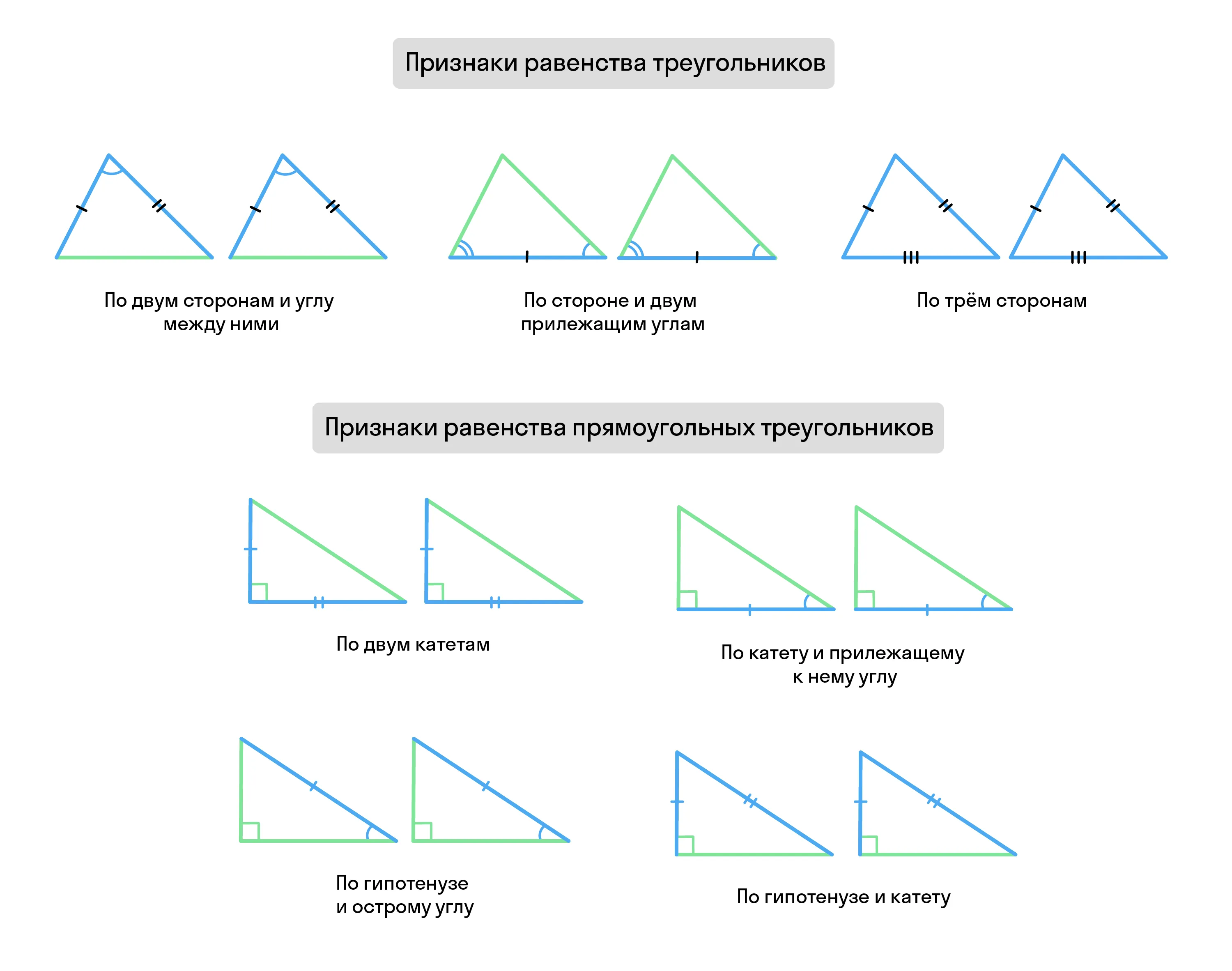
Подобие треугольников
Слово подобный можно связать со словами «схожий, родственный, напоминающий».
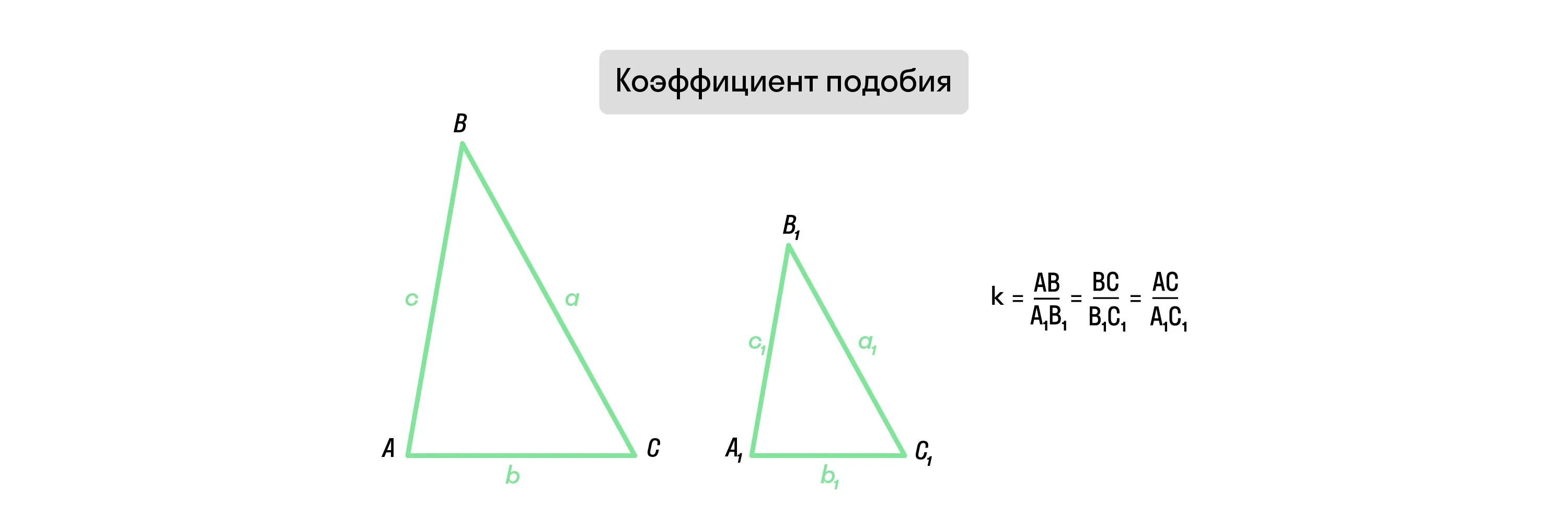
Подобные треугольники — такие треугольники, у которых совпадает форма, но не размер (длины сторон).
Не будет ошибкой сказать, что подобные треугольники представляют собой уменьшенные или увеличенные копии друг друга, как если бы мы могли менять их размер по своему желанию.
Представьте: вы смотрите кино на экране планшета, а потом идёте на тот же фильм в кинотеатр. Размер экранов будет значительно отличаться, но сами пропорции будут оставаться прежними: герои фильма будут выглядеть такими же, вне зависимости от размера экрана, не будет искажений их тел или лиц.
Коэффициент подобия — это число k, равное отношению сходственных сторон подобных треугольников.
Существует три признака подобия треугольников.
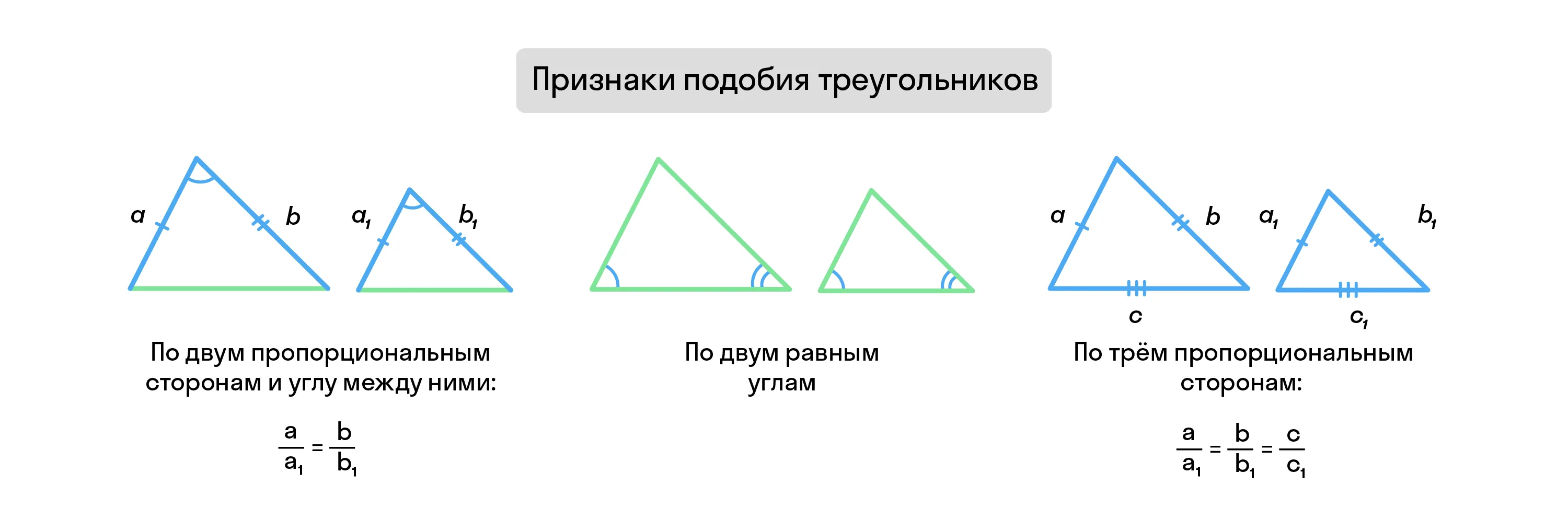
Признаки подобия треугольников — тема, которая очень часто используется при решении задач. Если в задаче один треугольник разделён на несколько треугольников с помощью биссектрис, высот, медиан, и вы не знаете, с чего начать — проверьте подобие: в 8 случаях из 10 это будет являться ключом к решению всей задачи.
Вписанная и описанная окружность
Если стороны треугольника являются касательными к окружности, то такая окружность называется вписанной.
Если окружность содержит все вершины треугольника, то такая окружность называется описанной.
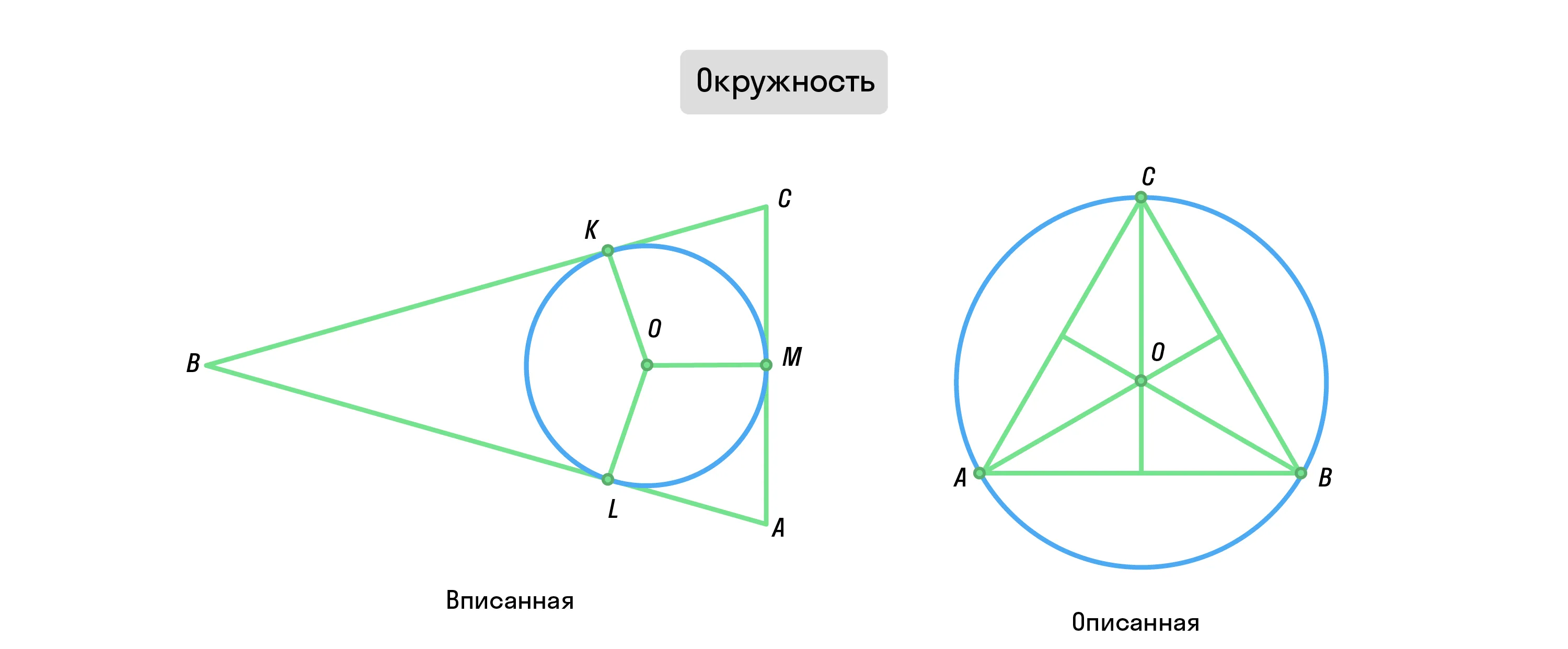
В любой треугольник можно как вписать окружность, так и описать окружность около него!
Для решения задач понадобятся следующие свойства и формулы:
|
Вписанная в треугольник окружность |
Описанная около треугольника окружность |
|---|---|
|
|
Свойства углов и сторон треугольника
Если в прямоугольном треугольнике для нахождения сторон используют теорему Пифагора, то для остро- и тупоугольных треугольников пользуются популярностью теоремы синусов и косинусов.
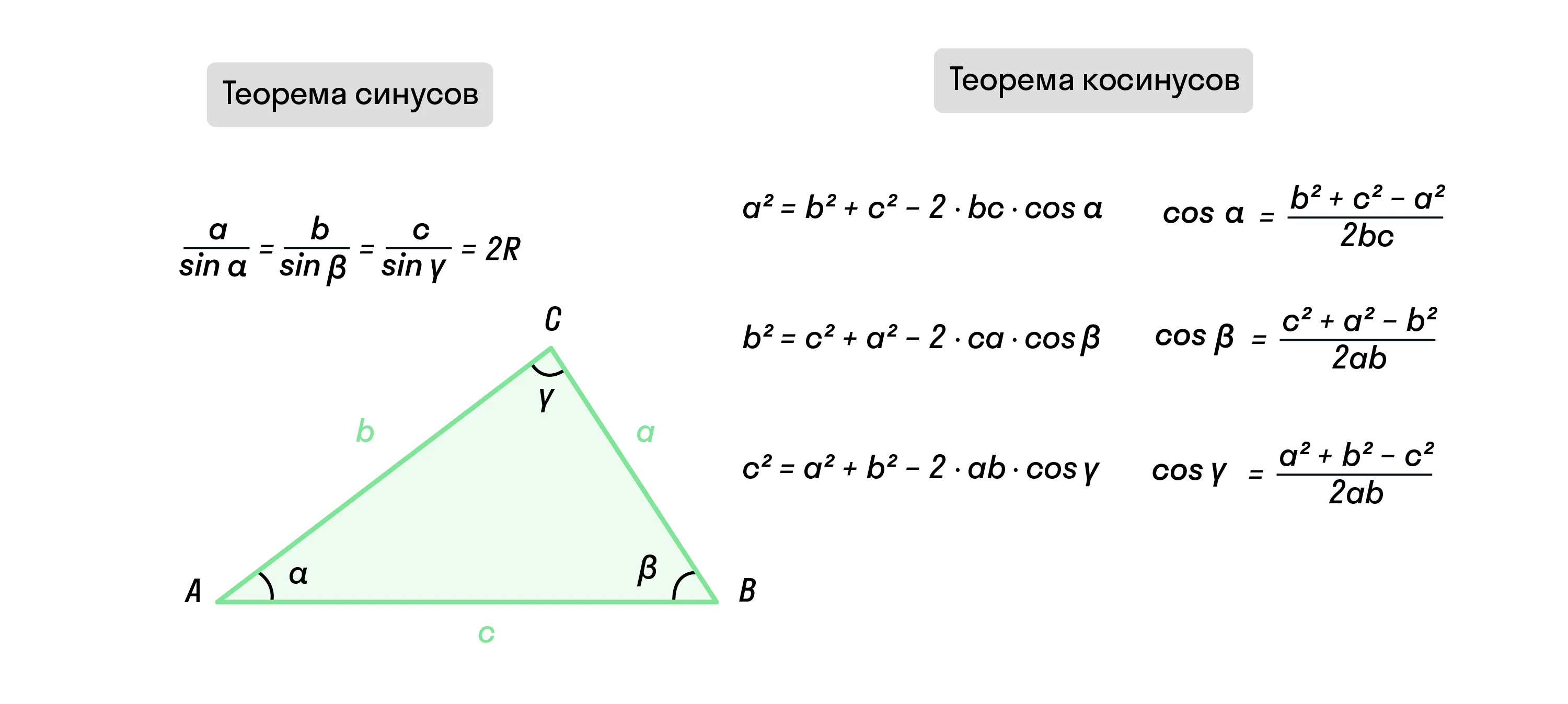
Помимо этих теорем, не забывайте следующие свойства:
-
сумма углов любого треугольника равна 180°;
-
сумма острых углов прямоугольного треугольника равна 90°;
-
внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним;
-
в треугольнике напротив большего угла лежит бо́льшая сторона, напротив меньшего угла — меньшая сторона;
-
в треугольнике любого типа соблюдается неравенство — сумма двух сторон строго больше длины третьей:
a + b > c
c + b > a
a + c > b
Как вы уже заметили, тема «Треугольники» включает в себя множество формул, правил, свойств и теорем. Лучше запомнить их поможет наш бесплатный тренажер ЕГЭ, в котором вы сможете решать типовые задачи и применять свои знания на практике. Пользуйтесь сами и отправляйте ссылку друзьям — обсуждайте задачи, сверяйте ответы и готовьтесь к экзаменам и контрольным вместе!
