Четырёхугольники: виды, формулы, свойства

Определение и общие свойства четырёхугольников

Четырёхугольник — геометрическая фигура, у которой 4 вершины и 4 стороны.

Два универсальных свойства:

• У любого четырёхугольника сумма углов равна 360°.

• Периметр четырёхугольника — сумма длин всех его сторон: P = a + b + c + d.

Правильный четырёхугольник — четырёхугольник, у которого все стороны и все углы равны. То есть, другими словами, это квадрат.

Четырёхугольники, как и любые многоугольники, бывают выпуклые и невыпуклые. В выпуклых все диагонали находятся внутри фигуры, в невыпуклых хотя бы одна диагональ выходит за пределы фигуры.

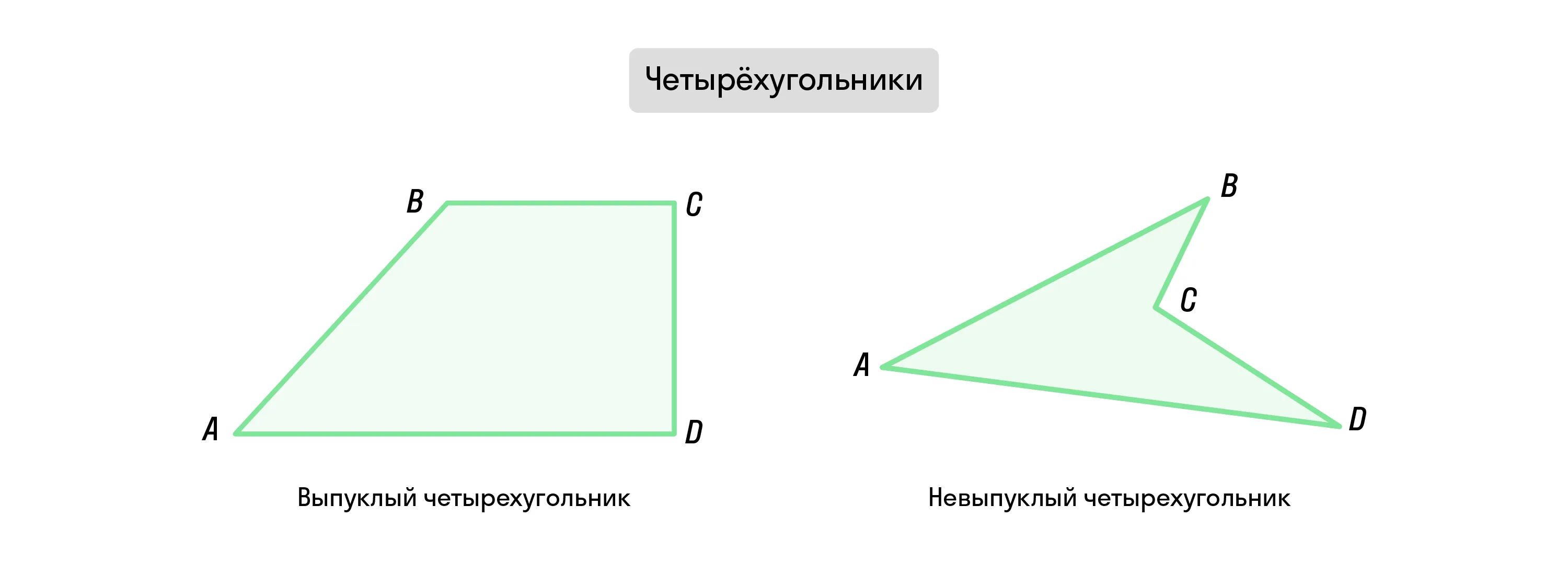
В школьной программе большее внимание уделяется именно выпуклым фигурам, так как их проще исследовать, выводить и доказывать для них теоремы. К выпуклым четырёхугольникам относят параллелограмм, квадрат, прямоугольник, ромб, трапецию. Каждая из этих фигур имеет как свои отличительные характеристики, так и то, что объединяет её с другими родственными фигурами.

Давайте подробно рассмотрим каждую из них.

Параллелограмм: определение, свойства, основные формулы

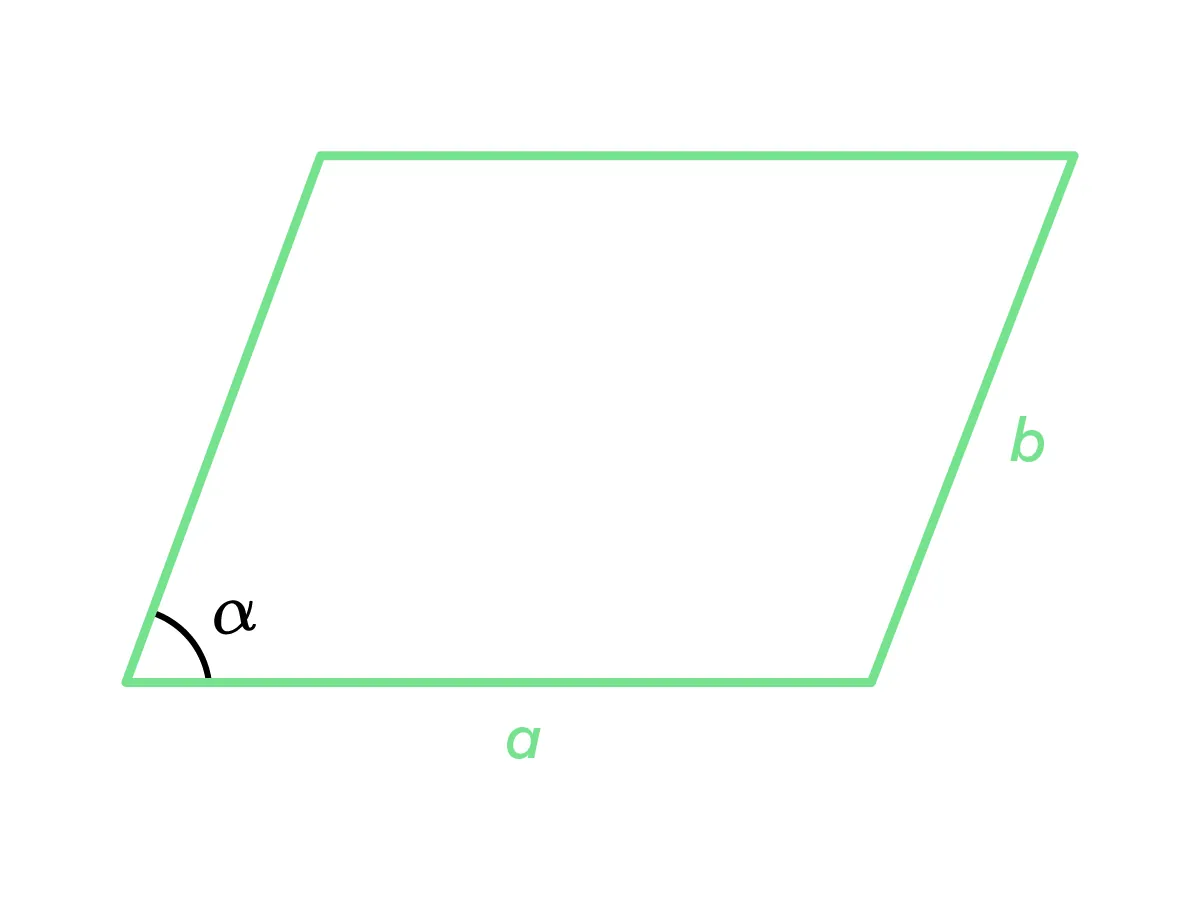
Параллелограмм — четырёхугольник, у которого стороны попарно параллельны.

Свойства:

• Противолежащие углы параллелограмма равны.

  

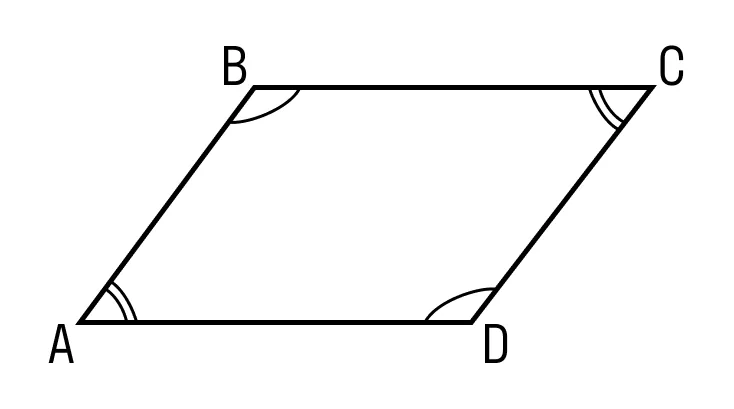
• Противолежащие стороны параллелограмма равны.

  

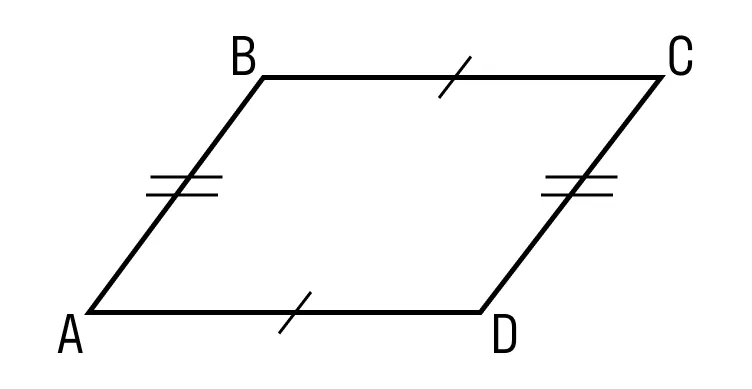
• Сумма углов, прилежащих к одной стороне, равна 180°.

• Диагонали параллелограмма в точке пересечения делятся пополам.

  

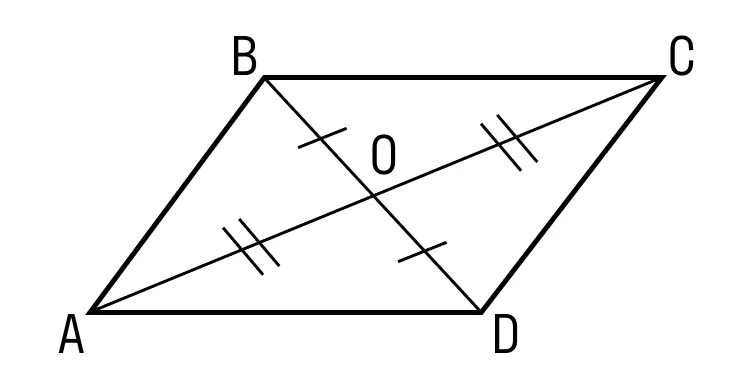
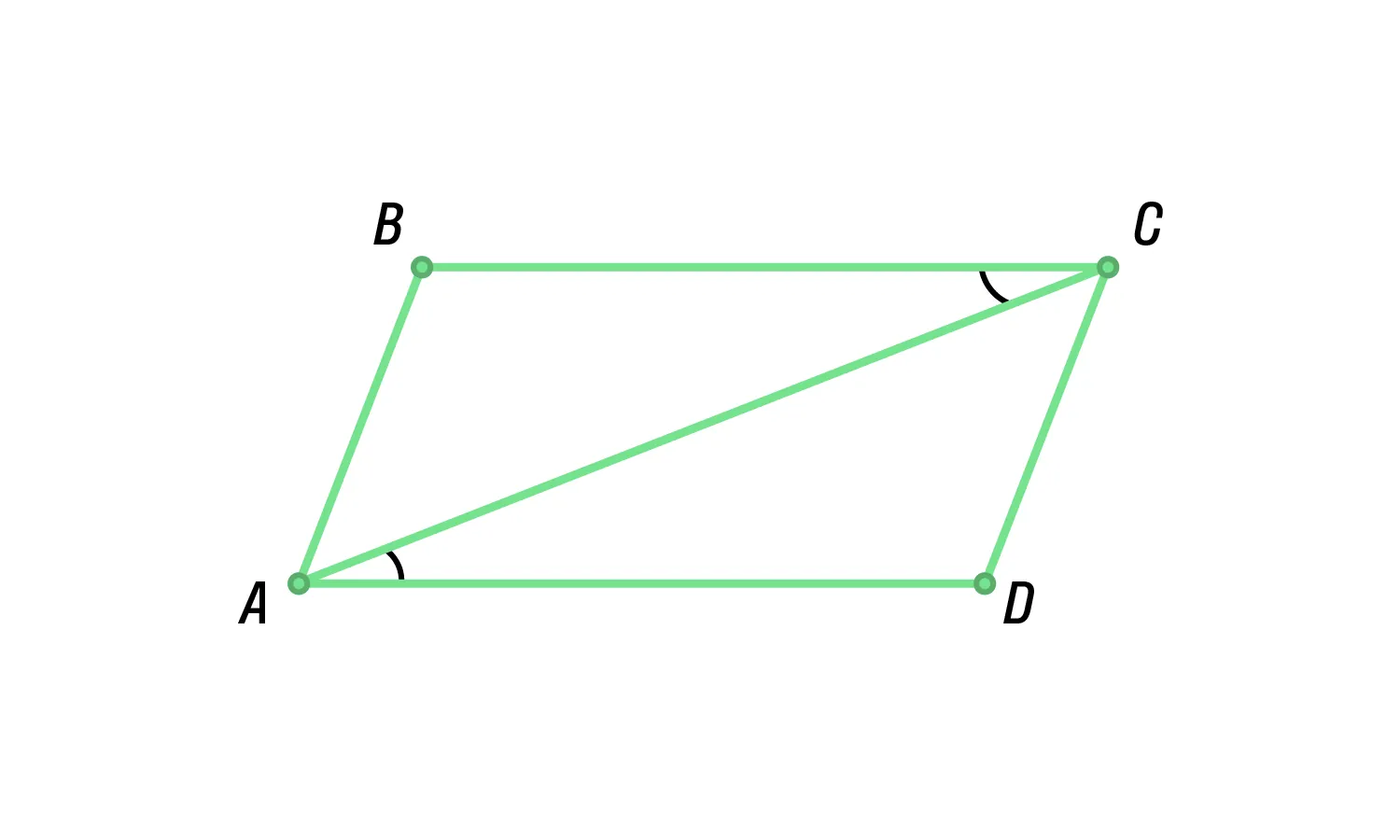
• Диагональ делит параллелограмм на два равных треугольника.

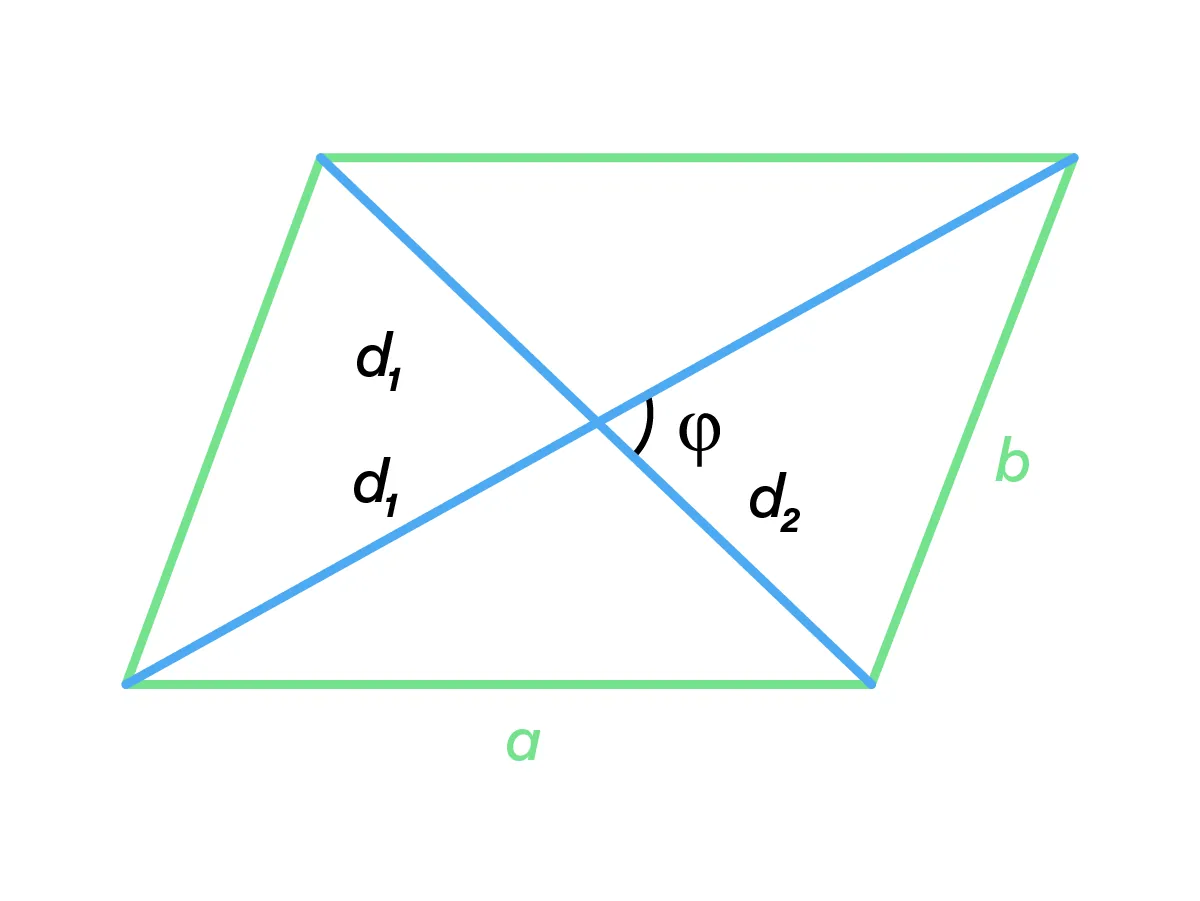
• В параллелограмме диагонали d₁, d₂ и стороны a, b связаны следующим соотношением: d²₁ + d²₂ = 2(a² + b²).

• Биссектриса, проведенная из угла параллелограмма, отсекает от него равнобедренный треугольник.

  

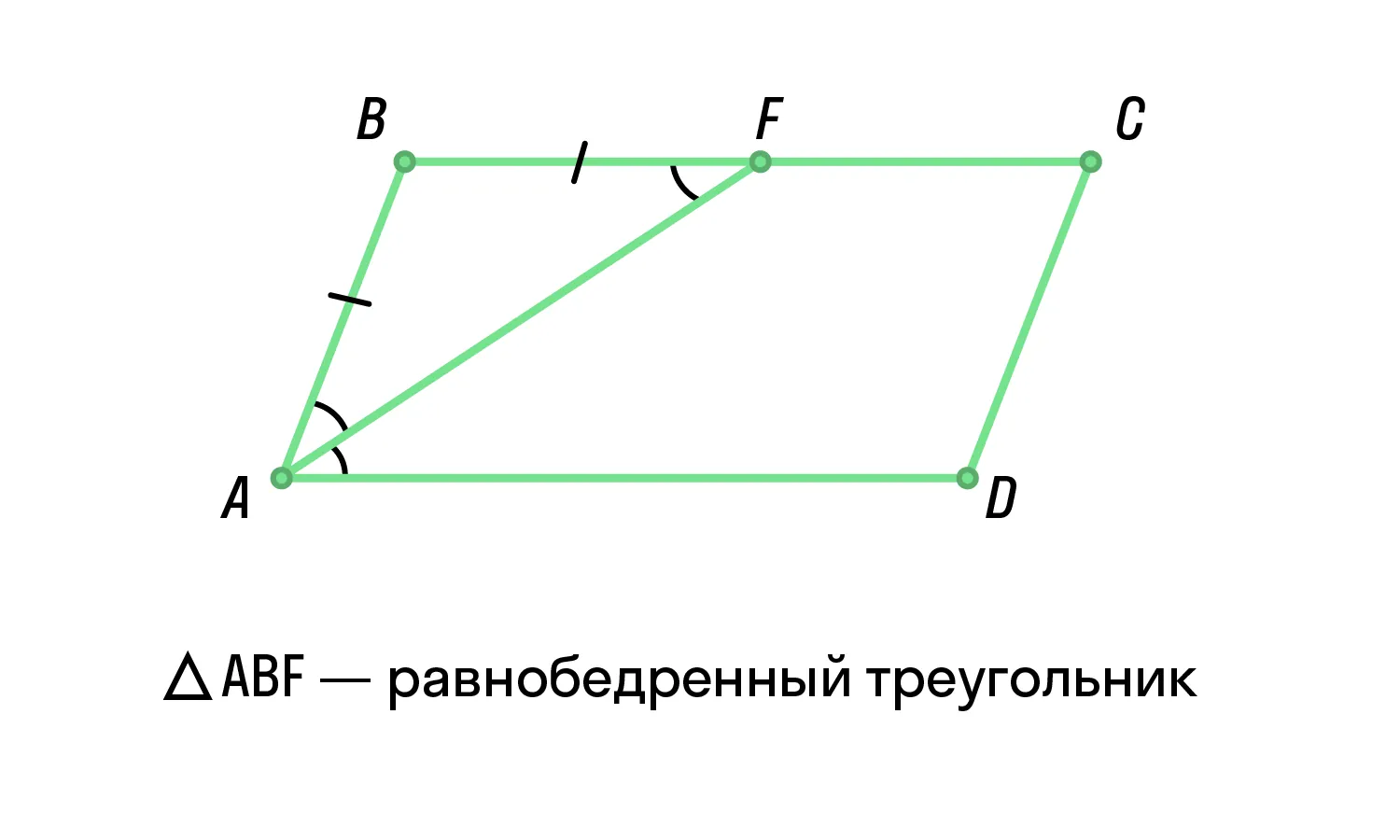
• Биссектрисы углов, принадлежащих одной стороне параллелограмма, пересекаются под прямым углом.

  

Так как по определению в параллелограмме стороны попарно параллельны, диагонали можно считать , а значит, накрест лежащие углы равны.секущими

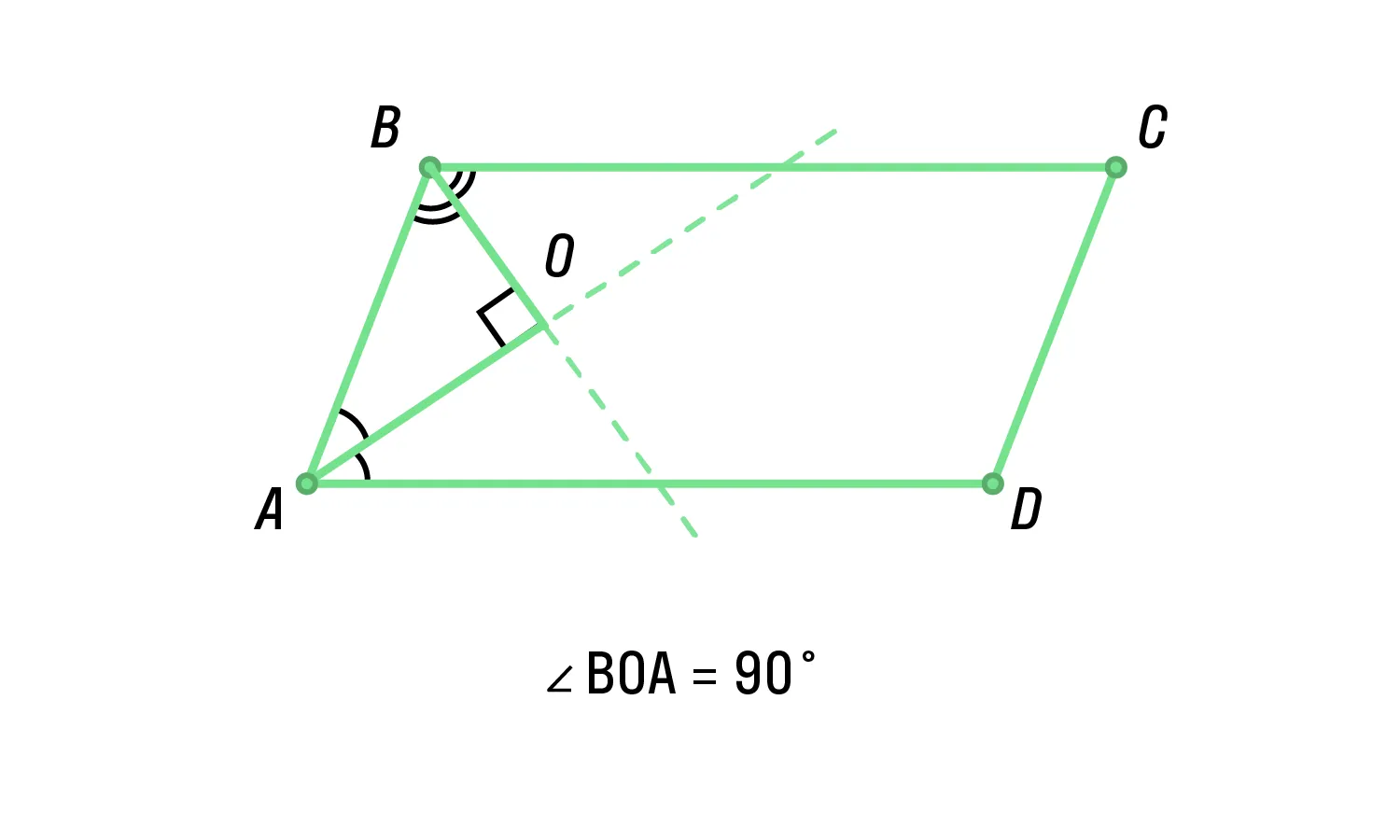
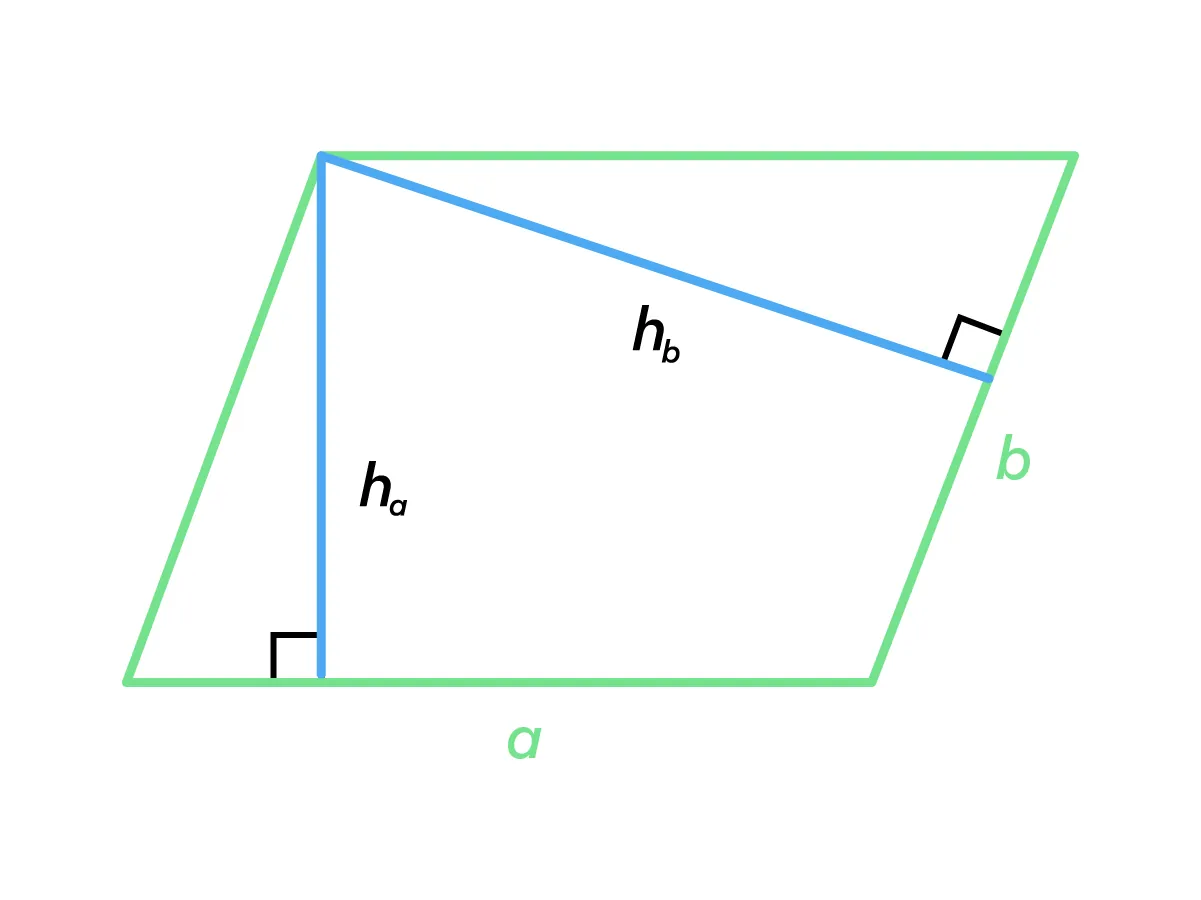
Площадь параллелограмма можно рассчитать по следующим формулам:

Параллелограмм — важная фигура в геометрии, на которую равняются другие четырёхугольники. Практически все из них — прямоугольник, квадрат и ромб — наследуют свойства параллелограмма с учётом своих особенностей.

Это интересно

На основных свойствах параллелограмма устроена работа штурманской линейки. С её помощью вы можете быстро снять с карты необходимые координаты заданных точек, или же наоборот — нанести точки по заданным координатам, а также с высокой найти расстояние между точками на карте.

170.4K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Прямоугольник: определение, свойства, основные формулы

Прямоугольник — параллелограмм, у которого все углы равны.

Отличие от параллелограмма есть в названиях сторон фигуры: в прямоугольнике длинную сторону принято называть длиной, а короткую — шириной, для сторон параллелограмма особенные наименования не используются.

Помимо всех свойств, присущих параллелограмму, у прямоугольника есть уникальные черты:

• Диагонали прямоугольника равны.

• Диагональ делит прямоугольник на два равных прямоугольных треугольника.

• Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности.

• Диагональ прямоугольника является диаметром описанной окружности.

• Стороны прямоугольника одновременно являются и его высотами.

• Вокруг любого прямоугольника можно описать окружность, т. к. сумма противоположных углов равна 180°.

Формулы для нахождения площади прямоугольника можно вывести из аналогичных для параллелограмма:

1. (т. к. высота, проведённая из вершины угла к противоположной стороне, совпадает с другой стороной прямоугольника).

2. (т. к. угол между сторонами — прямой, а ).

3. .

Это интересно

Золотой прямоугольник — это геометрическая форма, в которой отношение более длинной стороны к более короткой стороне равно соотношению всего прямоугольника к более длинной стороне. Такое соотношение примерно равно 1,618 и считается наиболее эстетичным и приятным для человеческого глаза.

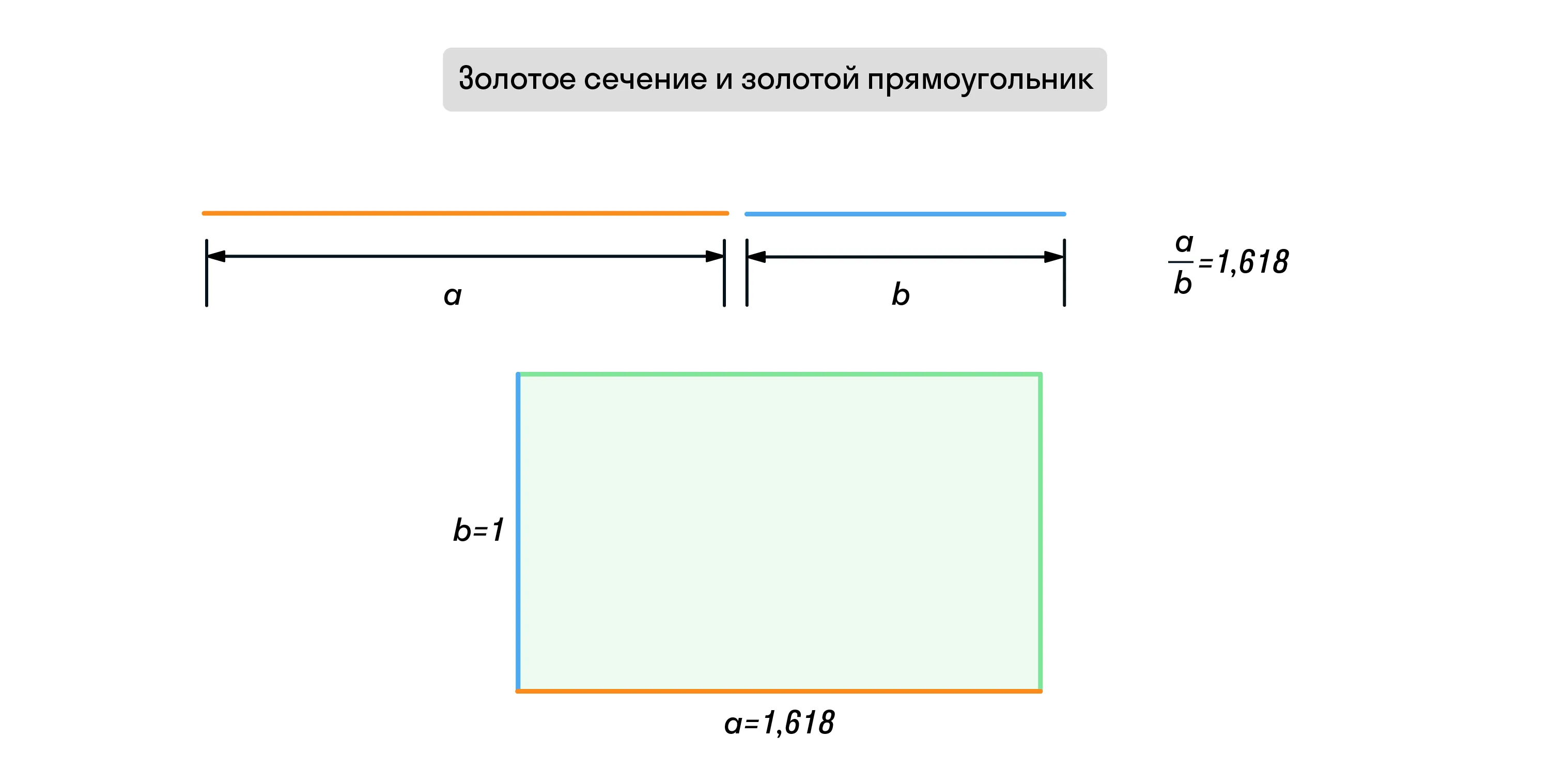
Ромб: определение, свойства, основные формулы

Ромб — параллелограмм, у которого все стороны равны.

Подобно прямоугольнику, ромб наследует все свойства параллелограмма и одновременно с этим имеет свои свойства:

• Диагонали ромба перпендикулярны друг другу.

• Диагонали ромба являются биссектрисами его углов.

• В любой ромб можно вписать окружность, так как суммы противоположных сторон равны.

• Центром вписанной окружности будет точка пересечения диагоналей ромба.

• В ромбе диагонали d₁, d₂ и сторона а связаны следующим соотношением: d²₁ + d²₂ = 4a².

Для нахождения площади ромба можно воспользоваться всеми аналогичными формулами для параллелограмма.

Это интересно

Термин «ромб» в переводе с латинского языка буквально означает «бубен» (ударный музыкальный инструмент). Раньше бубны изготовляли как раз такой формы. Поэтому и карточная масть бубны обозначается ромбиком.

Квадрат: определение, свойства, основные формулы

Эта фигура — что-то невероятное! 🤯

• Квадрат — это правильный многоугольник, так как у него равны все стороны и все углы.

• Квадрат — это параллелограмм, так как стороны попарно параллельны.

• Квадрат — это частный случай прямоугольника, так как все его углы — прямые.

• Квадрат — это частный случай ромба, так как все его стороны имеют одинаковую длину.

А значит, квадрат собрал в себе абсолютно все свойства четырёхугольников, перечисленных выше!

А ещё:

• Диагональ квадрата можно рассчитать по формуле .

• Вокруг любого квадрата можно описать окружность и в любой квадрат можно вписать окружность.

• Площадь квадрата можно рассчитать как , где r — радиус вписанной, R — радиус описанной окружности.

Трапеция: определение, свойства, основные формулы

Трапеция — четырёхугольник, у которого две стороны параллельны, а две — нет.

Параллельные стороны называются основаниями трапеции (верхним и нижним), а непараллельные стороны — боковыми.

Трапеции бывают:

• равнобокими или равнобедренными — их боковые стороны равны;

• прямоугольными — одна из сторон перпендикулярна основаниям.

Трапеция явно отличается от фигур, описанных выше: она не является «наследницей» параллелограмма, а значит, имеет отличные от него свойства (хотя некоторые из них всё равно совпадают).

Свойства трапеции:

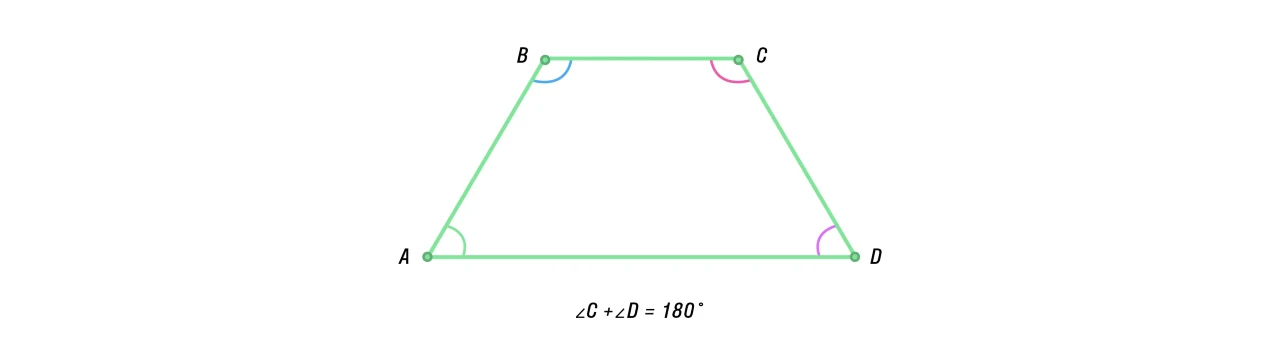
1. Сумма углов, прилежащих к боковой стороне трапеции, равна 180°.

   

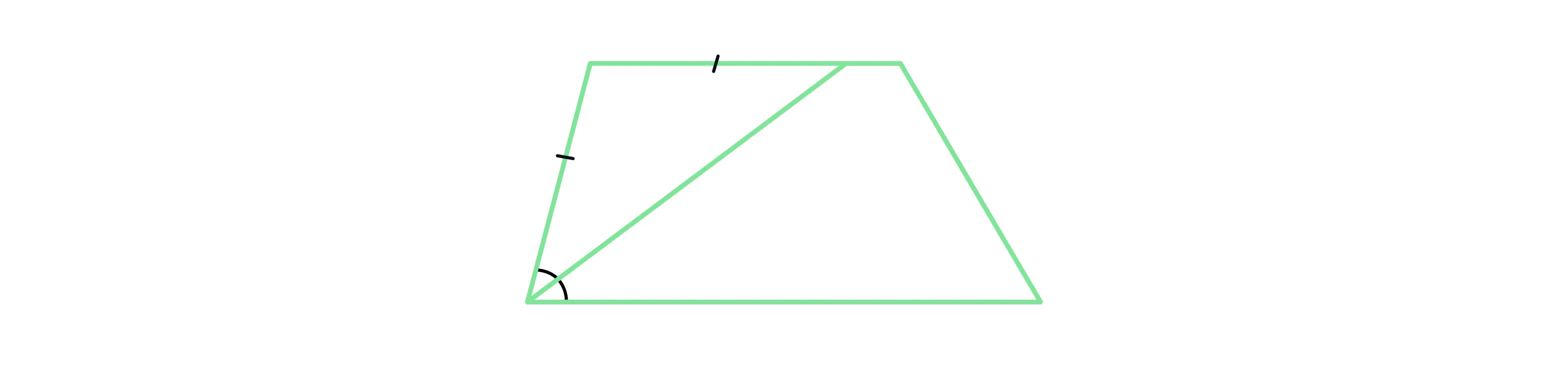
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

   

3. Треугольники AOD и COB, образованные при пересечении диагоналей, подобны: k = AD/BC.

   

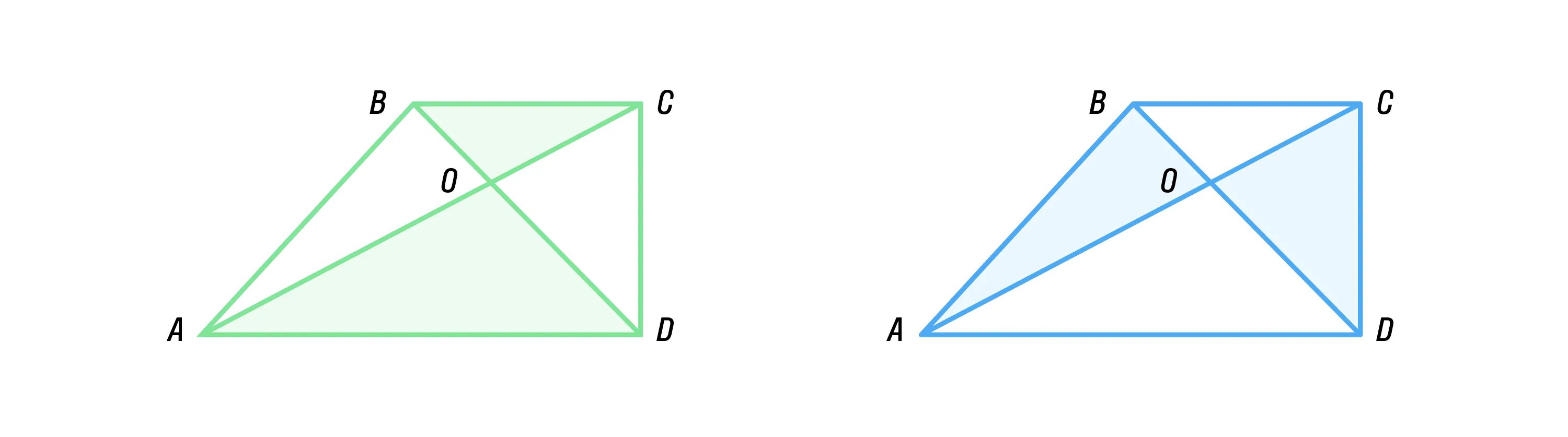
   Треугольники ABO и DCO имеют одинаковую площадь, т. е. они равновеликие.

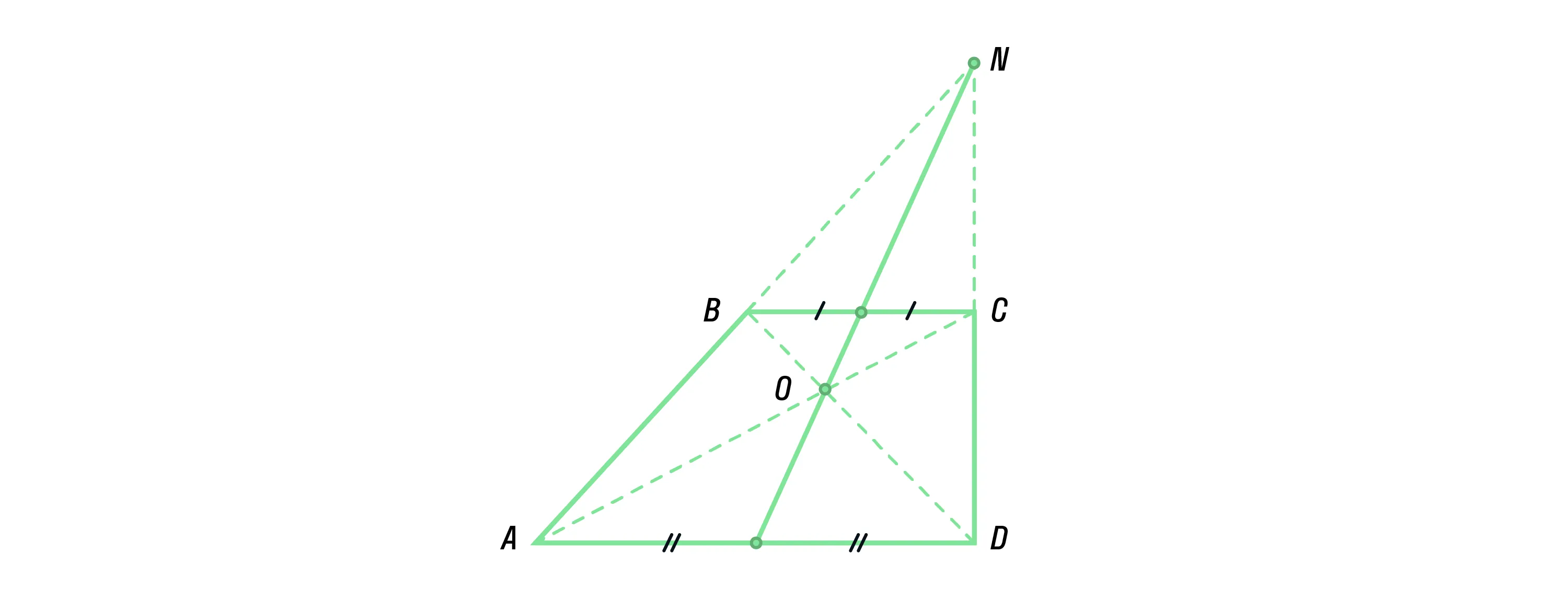
4. «Замечательное свойство трапеции»: точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

   

5. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

   

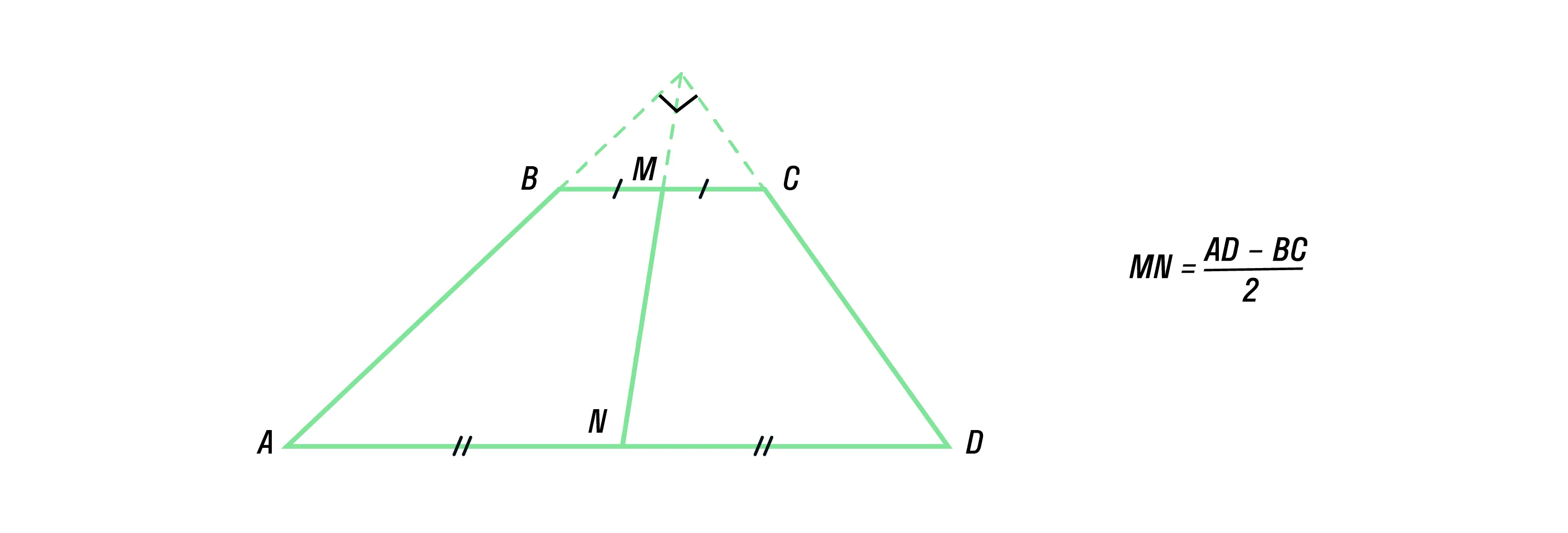
Отдельно можно выделить дополнительные свойства равнобедренных трапеций:

1. Диагонали в равнобедренной трапеции равны.

2. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

   

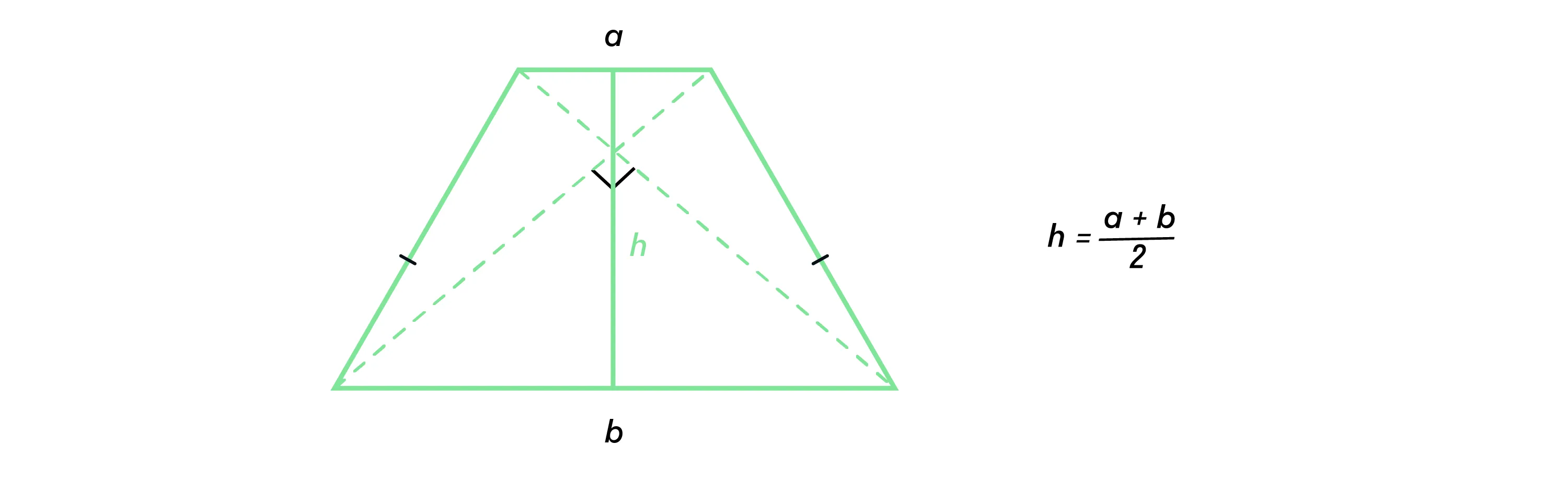
Площадь трапеции можно вычислить по формуле:

, где:

• a, b — основания трапеции;

• h — высота трапеции;

• MN — средняя линия трапеции.

Также можно воспользоваться дополнительными формулами:

, где:

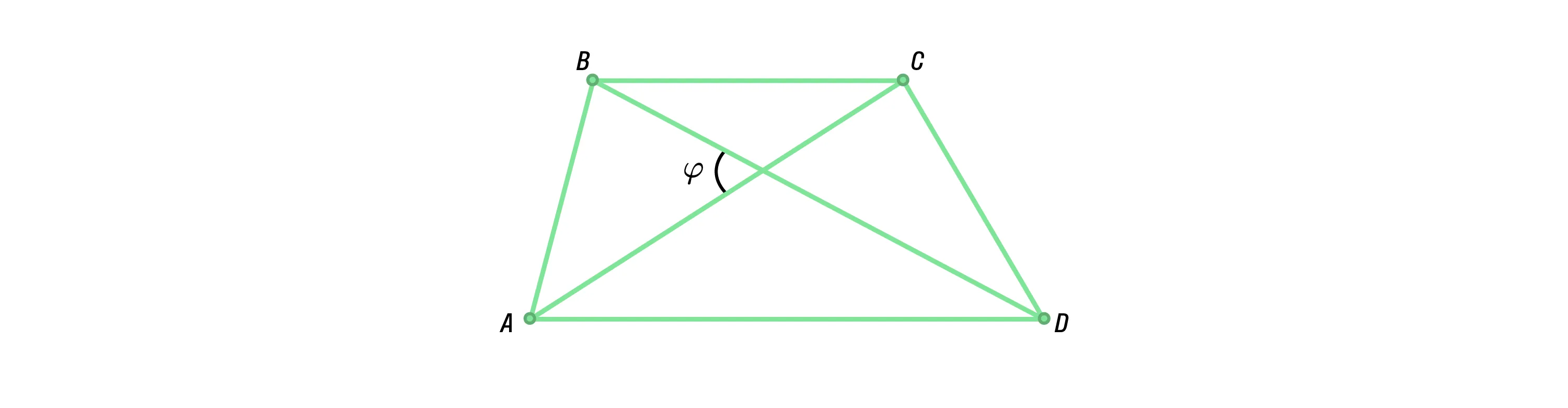
• d₁, d₂ — диагонали трапеции;

• — синус острого угла между ними.

, где:

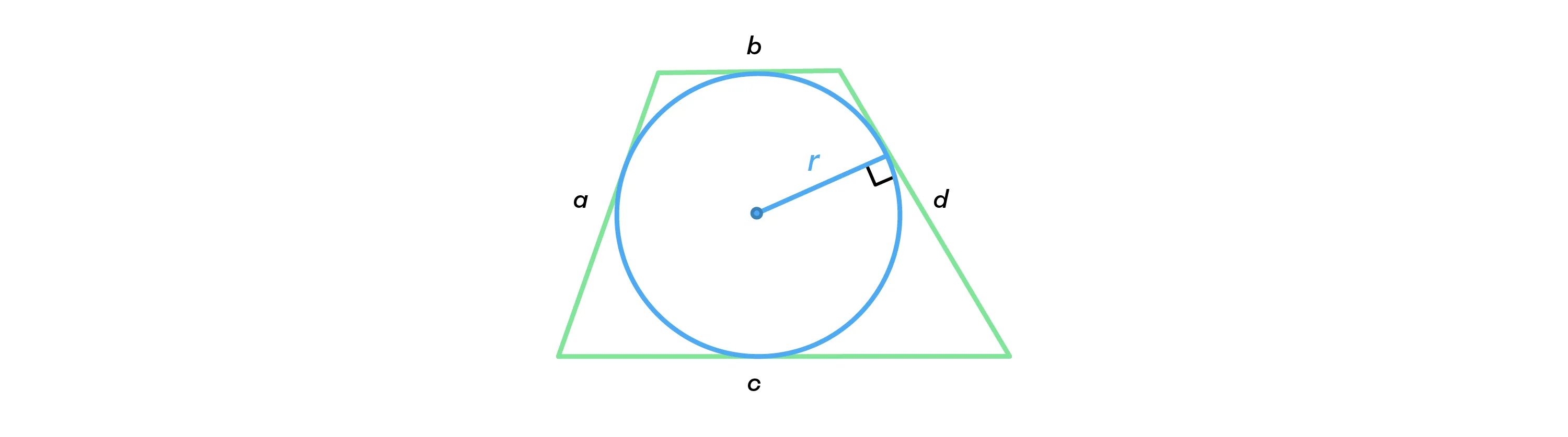
• p — полупериметр трапеции;

• r — радиус вписанной окружности.

Это интересно

Трапеция — это не только геометрическая фигура, но ещё и:

• гимнастический снаряд,

• юбка,

• кость запястья

• и номенклатурный лист топографической карты!

Четырёхугольники — это лёгкая и интересная тема, которую можно освоить за считанные дни. Проходите по ссылке и решайте оригинальные задачи в нашем бесплатном тренажёре ЕГЭ, практикуйтесь сами и приглашайте друзей: контрольные и экзамены — не за горами!