Многоугольники: определение и виды

Что такое многоугольник

Многоугольник — это геометрическая фигура, которая образована замкнутой ломаной линией, не имеющей пересечений с самой собой.

Каждое звено этой ломаной линии называется стороной многоугольника, а точки, в которых она «ломается» — его вершинами.

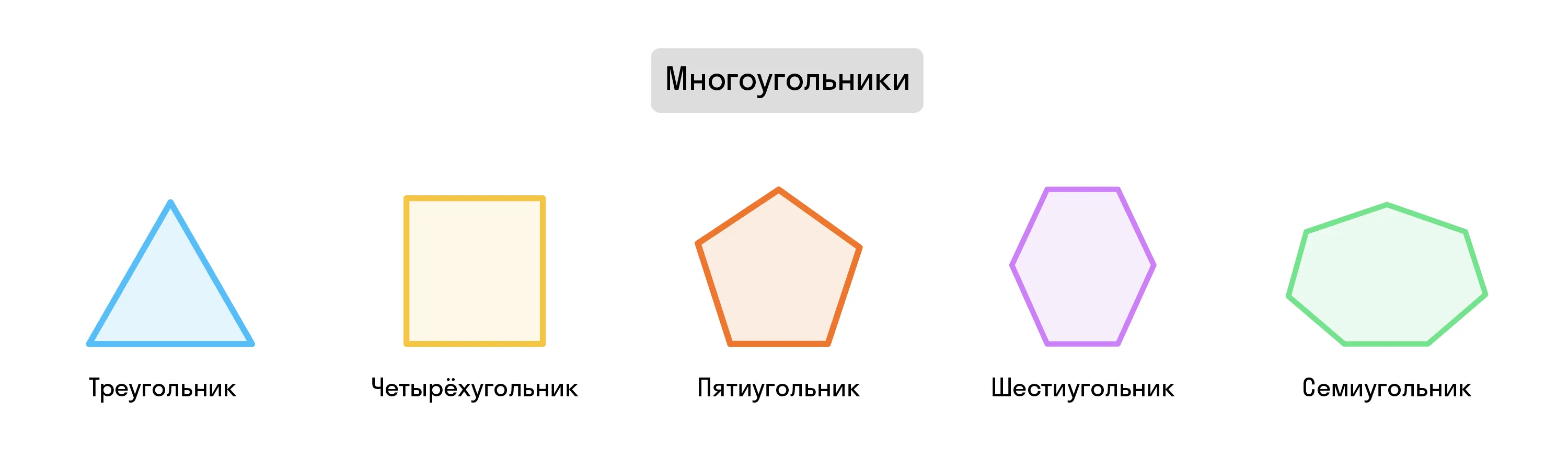
Также у многоугольника есть углы — это внутренние углы, которые образованы сторонами фигуры. Часто название многоугольника совпадает с количеством его углов. Многоугольник с 3 углами — это треугольник, с 4 — четырёхугольник, с 6 — шестиугольник и т. д. Многоугольников с 2 и менее углами не бывает.

Выпуклые и вогнутые многоугольники

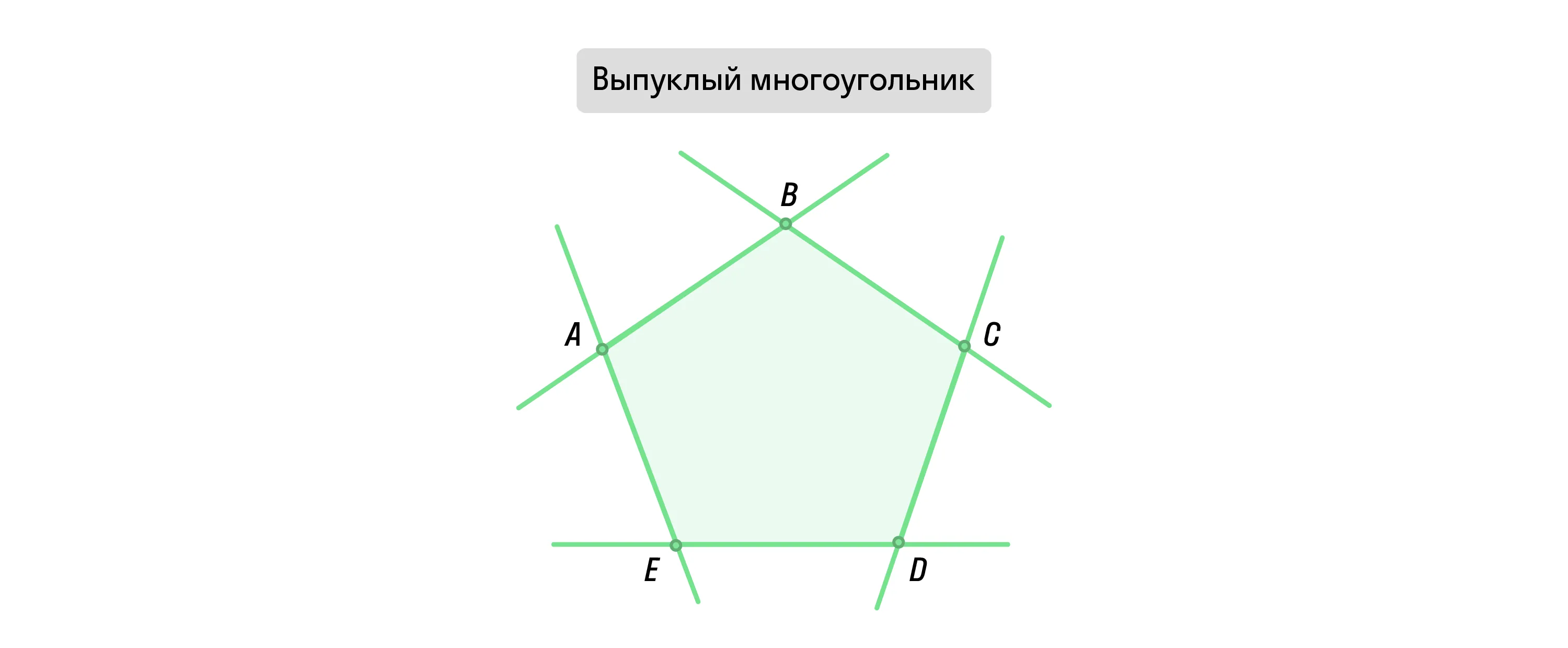
Выпуклым многоугольник называют тогда, когда прямая, проведённая через любую его сторону не пересекает плоскость самой фигуры.

Иначе говоря, весь многоугольник лежит по одну из сторон такой прямой. Все его внутренние углы меньше 180°. Сумма внутренних углов такого многоугольника равна , где — это число сторон многоугольника.

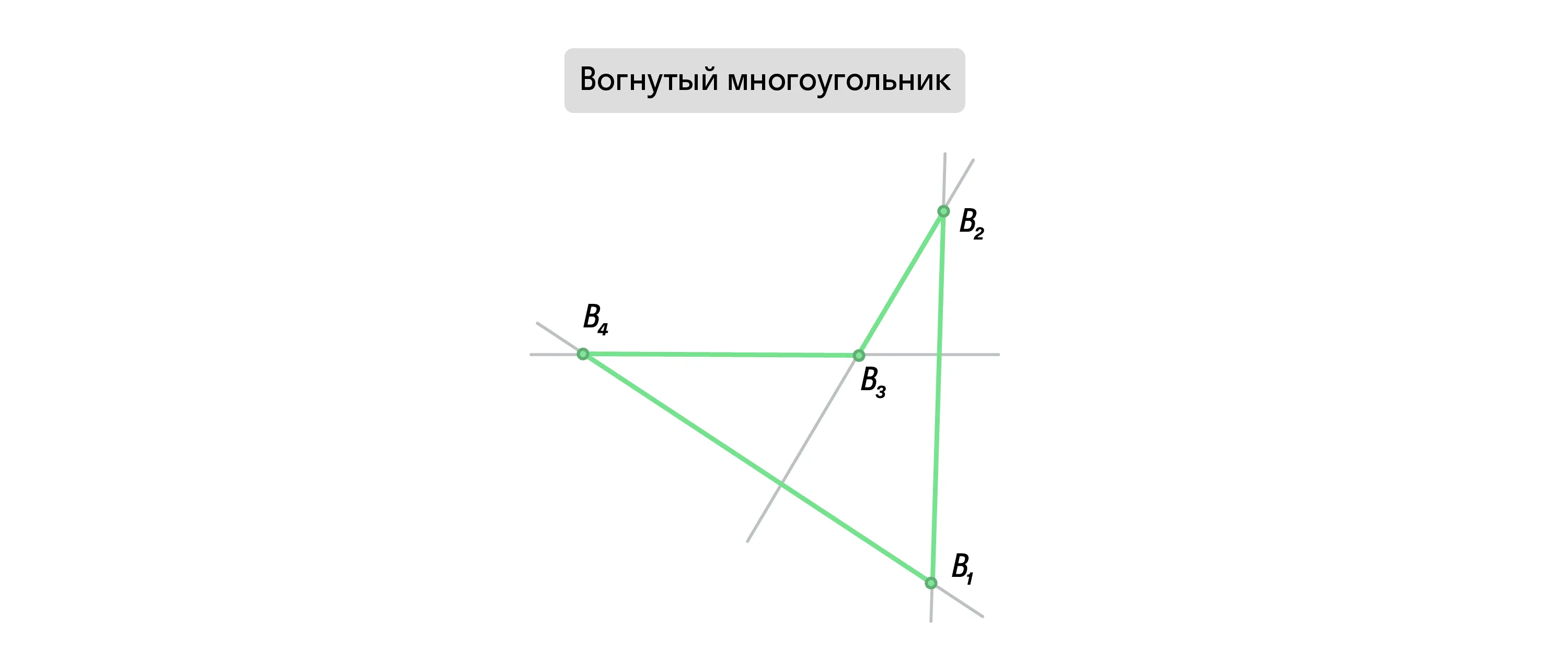
Вогнутым многоугольник называют тогда, когда прямая, проведённая через любую его сторону пересекает плоскость самой фигуры.

Такой многоугольник легко отличить — он «сгибается» внутрь в одной из сторон. При этом хотя бы один из его внутренних углов больше 180°.

178.1K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Периметр многоугольника

Периметр многоугольника — это сумма длин всех его сторон.

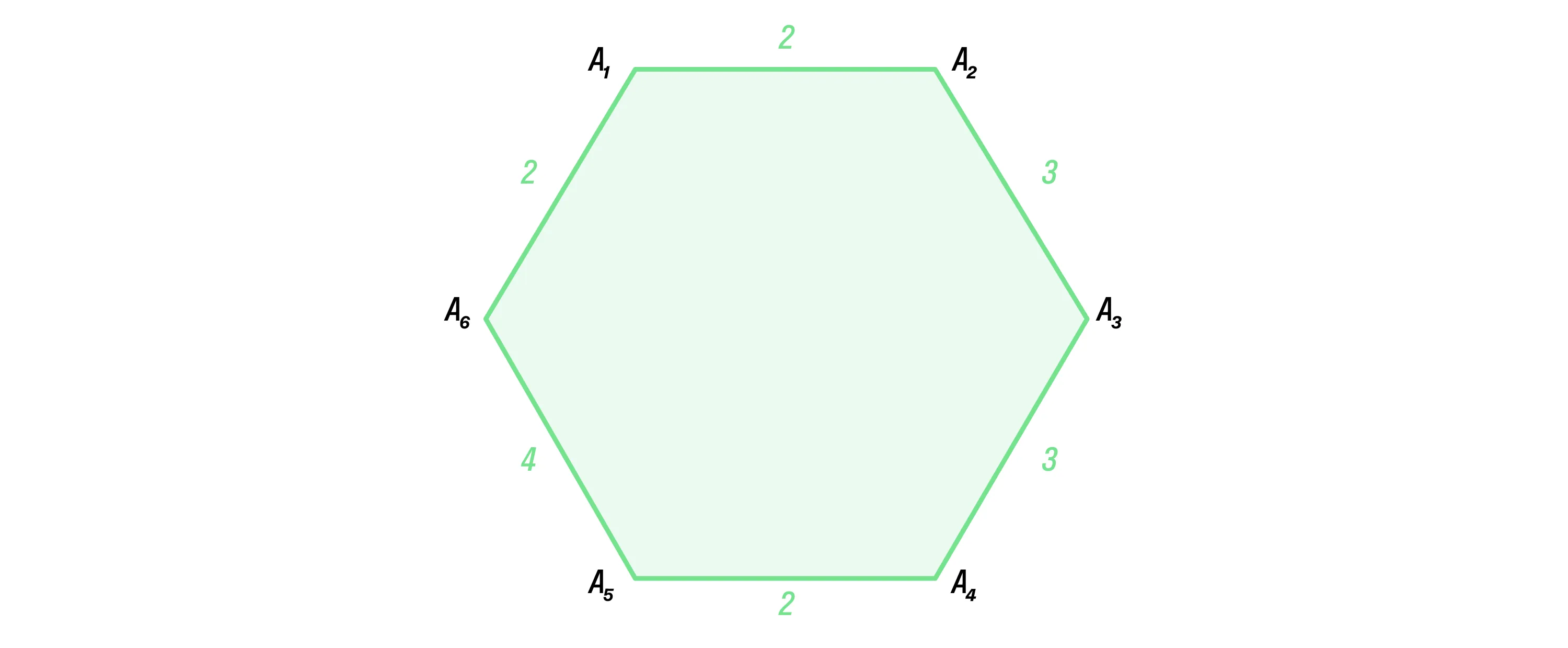
Для примера рассчитаем периметр шестиугольника на картинке ниже:

Диагональ многоугольника

Диагональ многоугольника — это отрезок, который соединяет вершины двух его углов, не имеющих общей стороны.

При этом у треугольника диагонали быть не может, потому что все его углы имеют общие стороны.

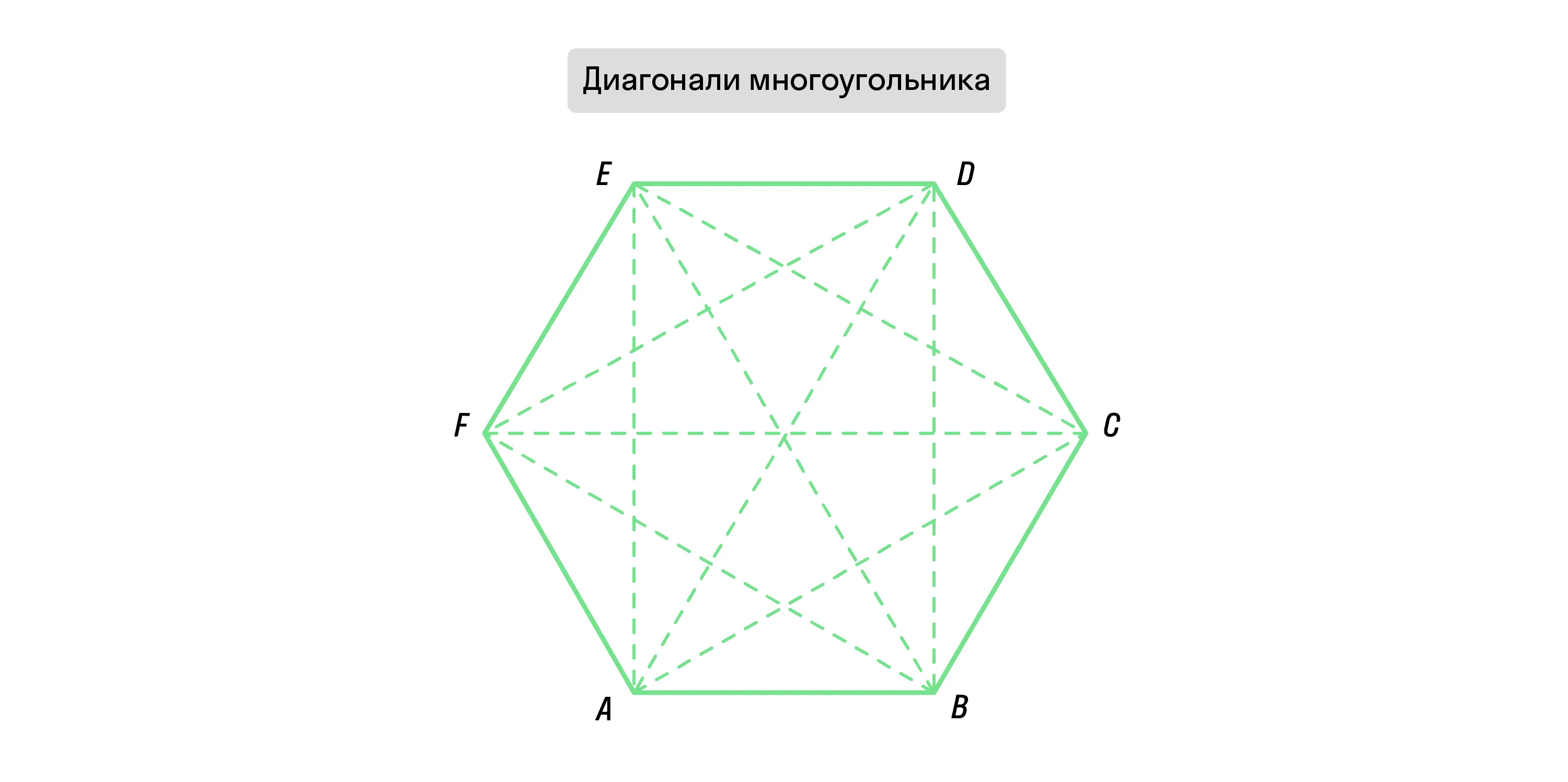
Вычислить количество диагоналей в многоугольнике можно по формуле , где — это количество углов. Так, для фигуры на картинке выше справедливы такие расчёты:

Если провести все возможные диагонали из одной вершины, они разделят фигуру на треугольники. При этом в случае с любым многоугольником, их будет на 2 меньше, чем углов: .

Правильные многоугольники

Правильный многоугольник — это выпуклый многоугольник, стороны и внутренние углы которого равны.

Такие фигуры ещё называют симметричными — их можно «сложить» пополам, при этом все стороны и вершины обеих частей совпадут.

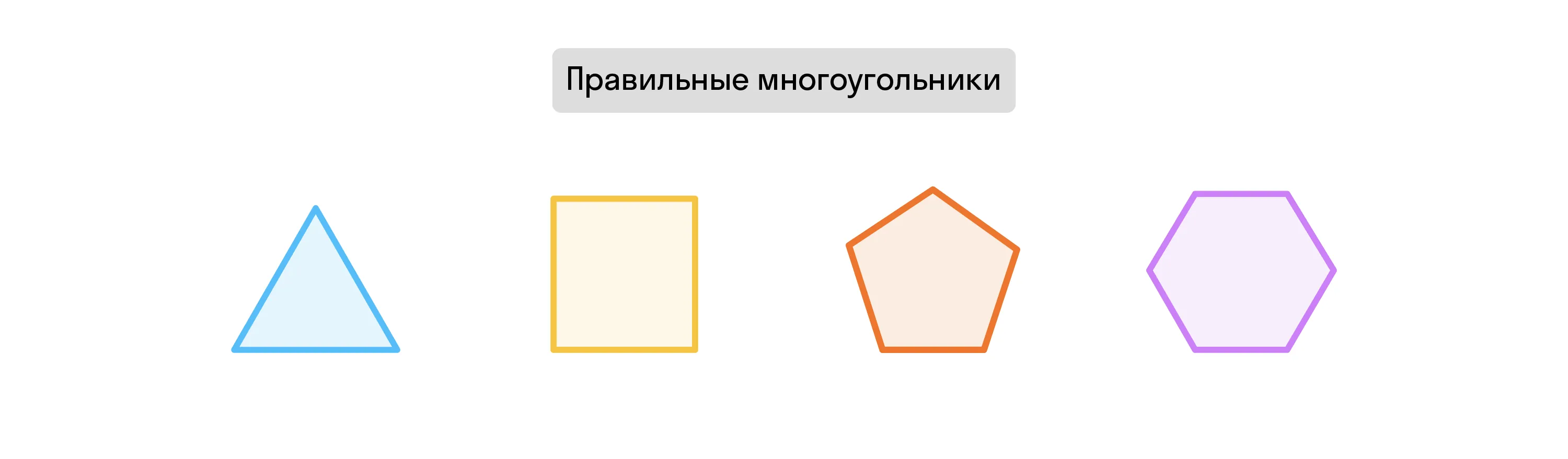
Ещё одно важное свойство: все биссектрисы углов между сторонами правильного многоугольника равны и проходят через его центр.

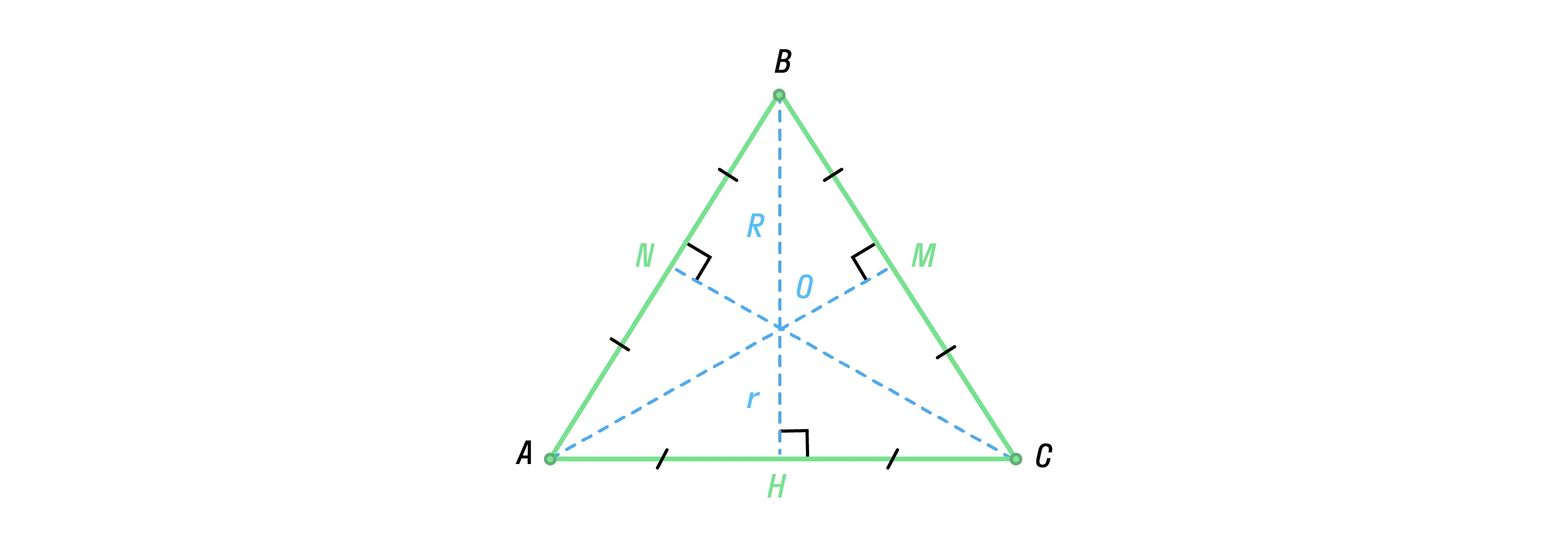
Особенности правильных многоугольников упрощают связанные с ними расчёты. Например, периметр такой фигуры: , где — длина её стороны, а — количество углов.

Правильный треугольник: все формулы

Формулы для правильных треугольников
Формула стороны через радиус вписанной окружности
Формула стороны через радиус описанной окружности
Формула радиуса вписанной окружности через длину стороны
Формула радиуса описанной окружности через длину стороны
Формула площади через длину стороны
Формула площади через радиус вписанной окружности
Формула площади через радиус описанной окружности
Угол между сторонами

Правильный четырёхугольник: все формулы

Формулы для правильных четырёхугольников
Формула стороны через радиус вписанной окружности
Формула стороны через радиус описанной окружности
Формула радиуса вписанной окружности через длину стороны
Формула радиуса описанной окружности через длину стороны
Формула площади через длину стороны
Формула площади через радиус вписанной окружности
Формула площади через радиус описанной окружности
Угол между сторонами

Правильный шестиугольник: все формулы

Формулы для правильных шестиугольников
Формула стороны через радиус вписанной окружности
Формула стороны через радиус описанной окружности
Формула радиуса вписанной окружности через длину стороны
Формула радиуса описанной окружности через длину стороны
Формула площади через длину стороны
Формула площади через радиус вписанной окружности
Формула площади через радиус описанной окружности
Угол между сторонами

Правильный восьмиугольник: все формулы

Формулы для правильных восьмиугольников
Формула стороны через радиус вписанной окружности
Формула стороны через радиус описанной окружности
Формула радиуса вписанной окружности через длину стороны
Формула радиуса описанной окружности через длину стороны
Формула площади через длину стороны
Формула площади через радиус вписанной окружности
Формула площади через радиус описанной окружности
Угол между сторонами

Повторить свойства многоугольников, а также потренироваться решать задачи на эту тему можно в Тренажёре ЕГЭ. В нём собраны все темы по математике, которые встретятся на экзамене базового и профильного уровня. Задания доступны бесплатно и в любое время.