Компланарность векторов

Понятие компланарности векторов

Как мы уже сказали, компланарность векторов связана с их расположением в пространстве. Чтобы понять, какие векторы называют компланарными, давайте рассмотрим несколько определений, которые раскрывают это понятие с разных сторон.

• Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.

  

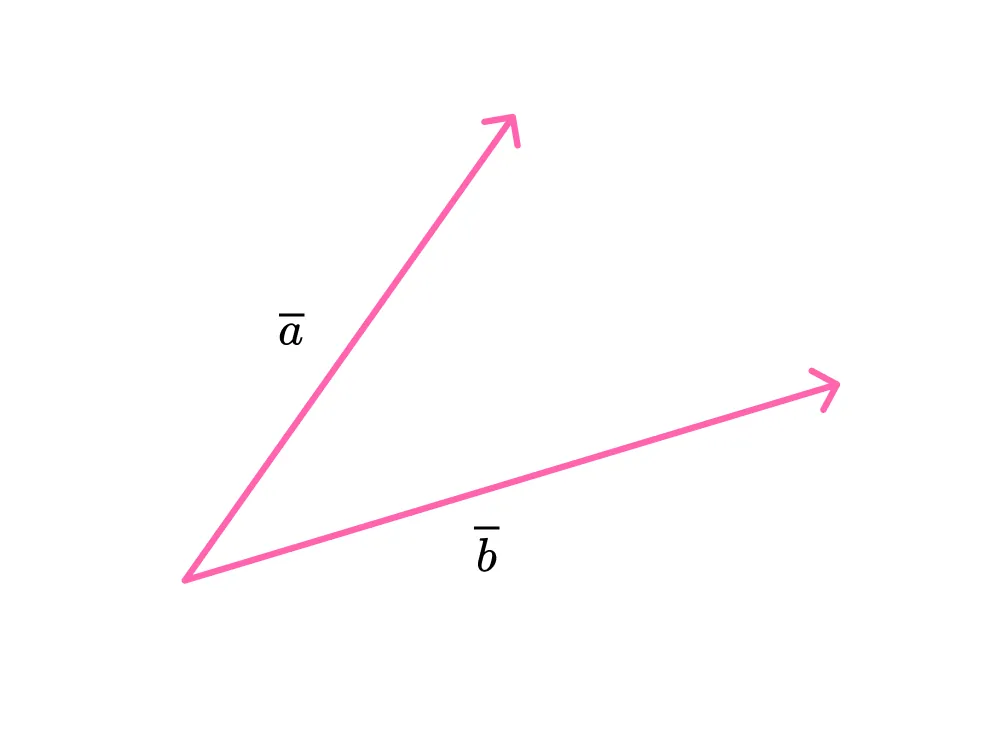
• Компланарные векторы — это векторы, которые лежат в одной плоскости или параллельны одной плоскости.

  

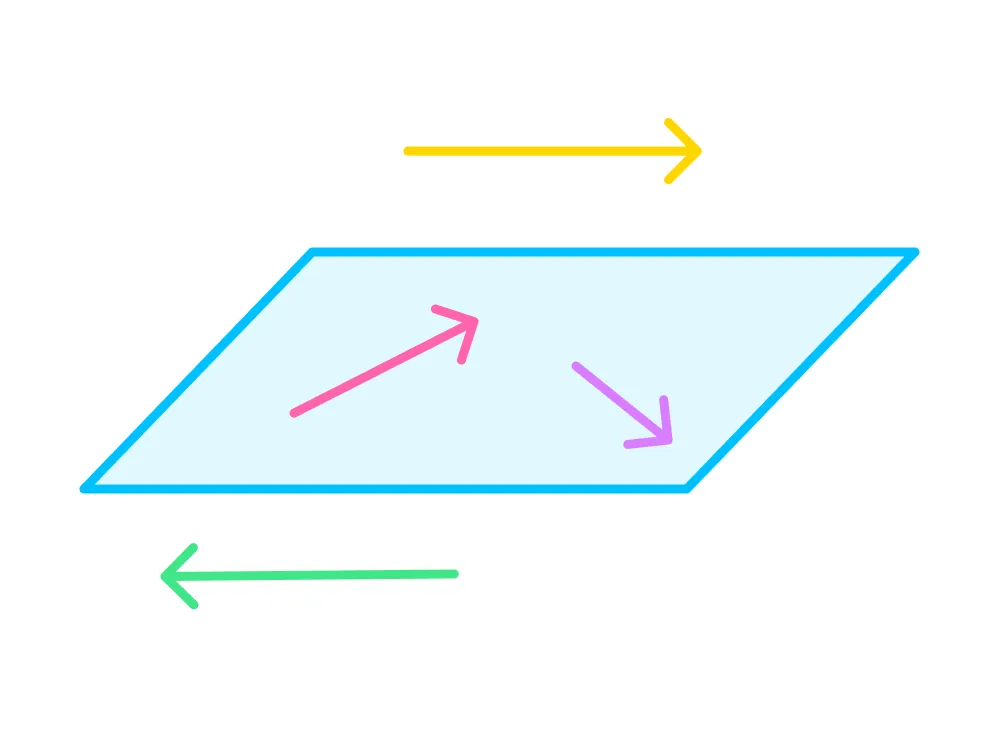
Как вы думаете, всегда ли можно найти плоскость, параллельную двум векторам? Да, вы абсолютно правы! Именно поэтому любые два произвольных вектора можно считать компланарными.

Но если векторов не два, а три, то, чтобы назвать их компланарными, нужно выполнить определенные условия.

Давайте рассмотрим эти условия компланарности на примере векторов а, b и с. Эти векторы компланарны, когда:

1. Пары векторов а и с, b и c, a и b компланарны между собой.

2. Хотя бы одна пара этих векторов коллинеарна (т. е. лежит на одной прямой или двух параллельных прямых).

3. Все три вектора лежат в одной плоскости.

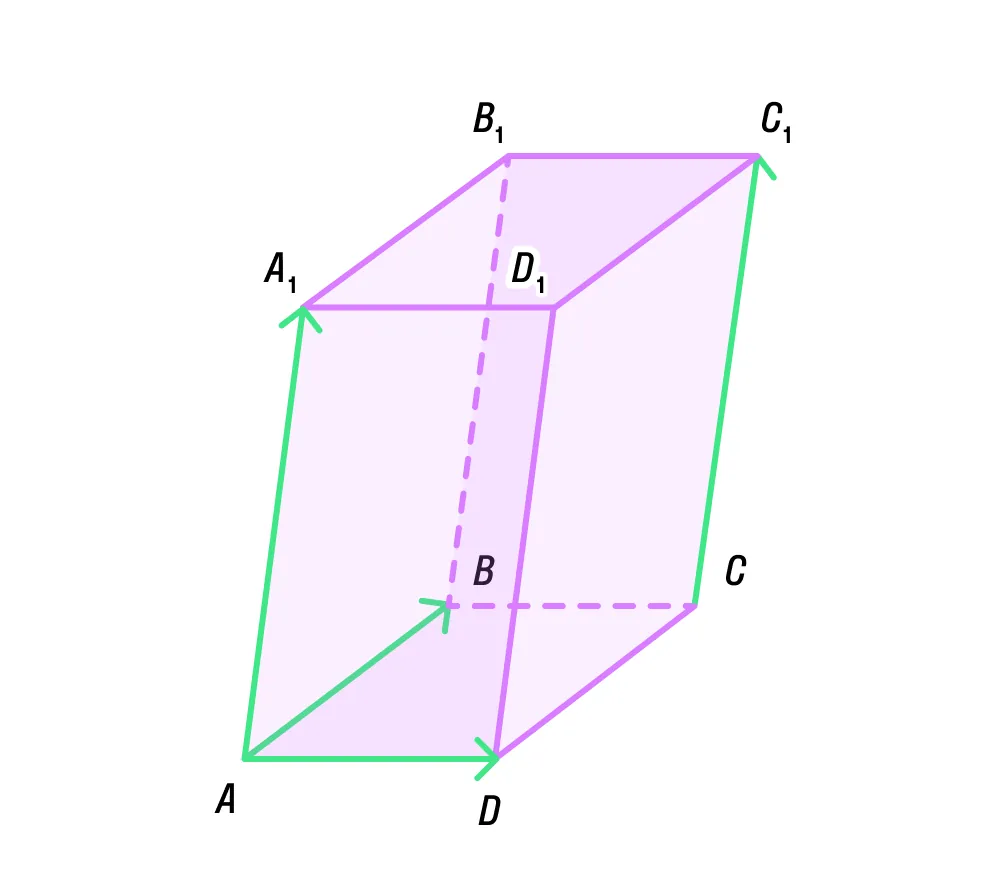
Давайте найдем пример компланарных и некомпланарных векторов, которые разместим на ребрах параллелепипеда:

• векторы АА₁, СС₁ и СВ компланарны, так как АА₁ и СС₁ коллинеарны;

• векторы АВ, DC и DD₁ компланарны, так как АB и DC коллинеарны;

• векторы CD, CB и CC₁ некомпланарны, так как они не лежат в одной плоскости и ни одна пара векторов не является коллинеарной.

Теоремы, связанные с компланарностью трех векторов

Теорема 1

Первая теорема не связана непосредственно с вопросом компланарности, но нам все равно необходимо ее вспомнить, так как она является вспомогательной.

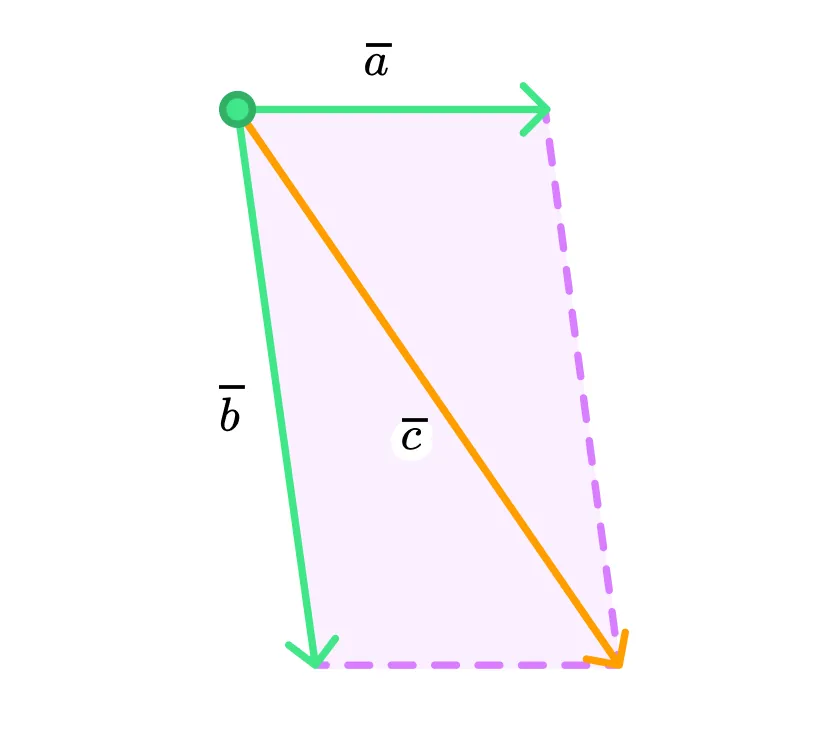
Звучит она так: любой произвольный вектор можно разложить по двум неколлинеарным векторам только с единственными коэффициентами разложения: .

Теорема 2

Если один из трех векторов можно разложить по двум другим векторам с единственными коэффициентами разложения, то эти векторы являются компланарными.

Давайте попробуем доказать эту теорему. Для этого возьмем три вектора: с, b и е, где .

1. Пусть векторы b и е являются коллинеарными. Тогда векторы с, b и е точно являются компланарными по свойству: если два из трех векторов коллинеарны, то все три можно считать компланарными.

2. Допустим, векторы b и е не являются коллинеарными. Тогда мы разложили вектор с по двум неколлинеарным векторам, что соответствует теореме 1. А это, в свою очередь, говорит о том, что векторы с, b и е лежат в одной плоскости и являются компланарными.

Теорема доказана!

Теорема 3

Если три вектора а, b и с являются компланарными, а векторы а и b — неколлинеарными, то вектор с можно разложить через а и b единственным образом: .

Эта теорема очень похожа на предыдущую, правда? Давайте обратим внимание на то, каким образом можно доказать то, что она верна.

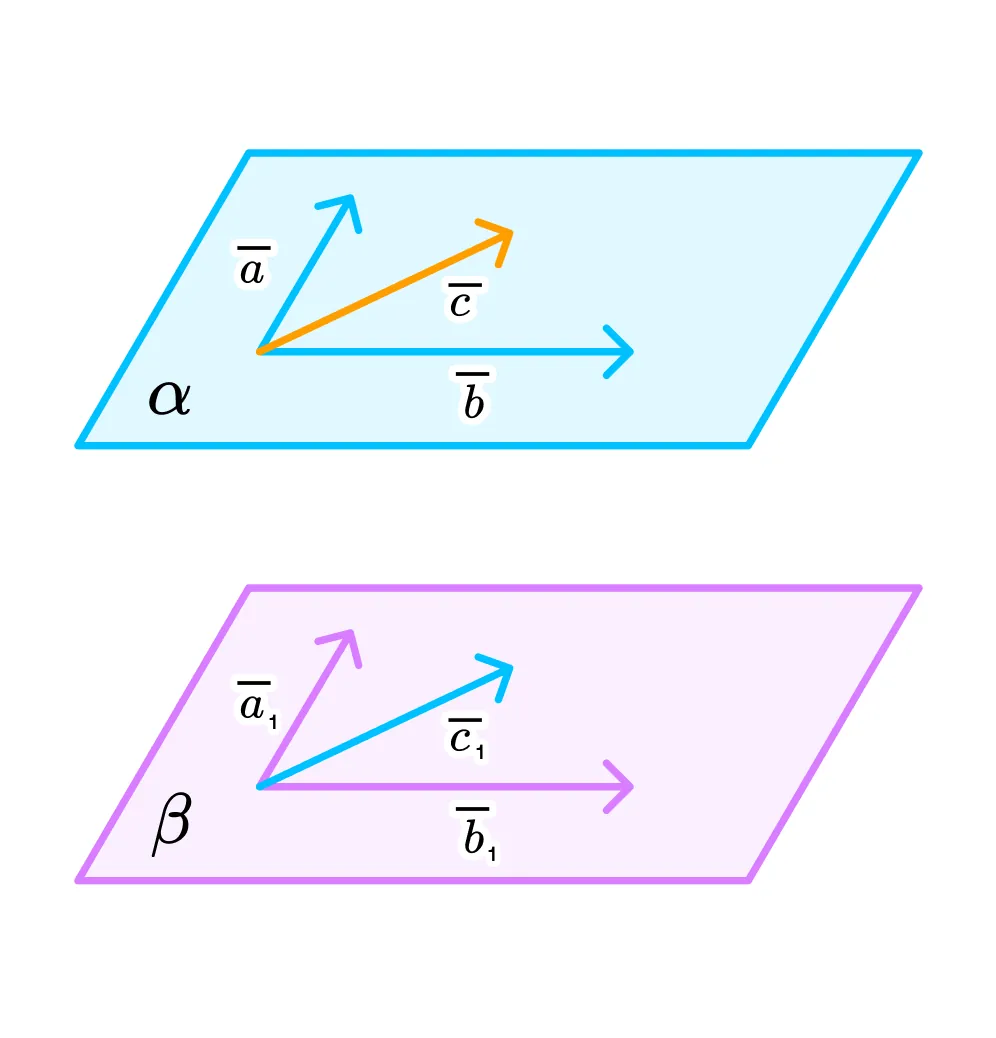
Раз векторы а, b и с компланарны, значит, существует такая плоскость, параллельная исходной, в которой можно построить векторы а₁ = а, b₁ = b, с₁ = с. Раз а и b неколлинеарны, значит, новые векторы а₁ и b₁ тоже будут неколлинеарными. А значит, согласно теореме 1, мы можем разложить вектор с₁ = ха₁ + уb₁.

Следовательно, .

178.1K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Признак и критерий компланарности векторов

С теоремами мы успешно разобрались — пришло время перейти к завершающей части. Для полной картины нам необходимо поговорить еще о некоторых нюансах, касающихся компланарных векторов.

Линейно зависимыми называются векторы , из которых можно составить линейную комбинацию, равную нулю: .

Смешанным (или векторно-скалярным) произведением трех векторов a, b, c (взятых в указанном порядке) называется скалярное произведение вектора a и векторного произведения b · c, т. е. число a (b · c), или (b · c) a.

Признаки компланарности векторов:

• Если смешанное произведение трех векторов равно нулю, то эти три вектора компланарны.

• Если три вектора линейно зависимы, то они компланарны.

Эти признаки редко подробно изучают в школьном курсе. Но ведь приятно знать то, о чем даже не догадываются твои одноклассники? 😉

Практика

Мы много узнали, теперь осталось закрепить теорию практическим заданием.

Дан параллелепипед АВСDА₁В₁С₁D₁. Разложите вектор D₁B₁ по DC и CB.

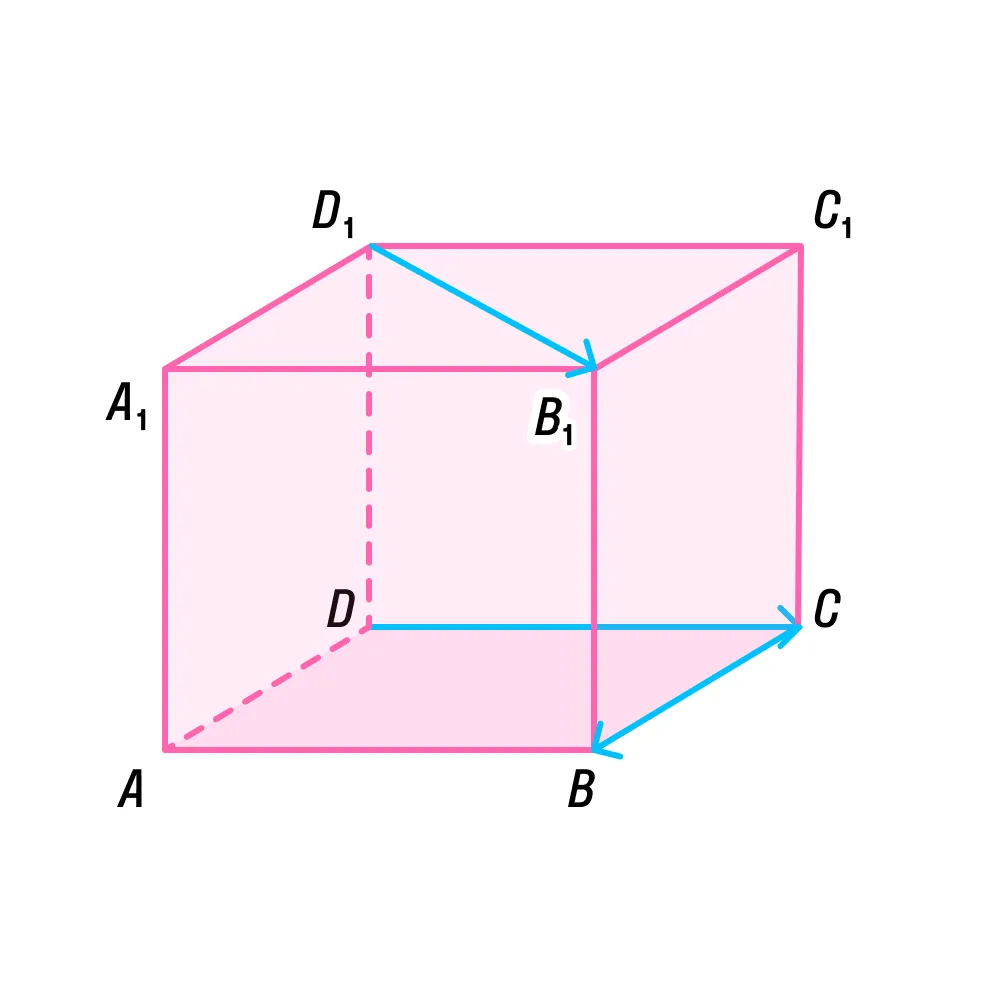
Решение.

Плоскости (АВС) и (А₁В₁С₁) параллельны, так как находятся на противоположных гранях параллелепипеда. Значит, векторы D₁B₁, DC и CB являются компланарными. Поэтому по теореме 2 мы сможем провести разложение D₁B₁ по DC и CB, причем единственным способом:

DB = D₁B₁, DC = D₁C₁, CB = C₁B₁.

Согласно правилу треугольника, DB = DC + CB.

А так как DB = D₁B₁, значит, и D₁B₁ = DC + CB.

В геометрии достаточно много тем, которые требуют детального изучения: в них есть теоремы, аксиомы, интересные логические умозаключения. Разобраться во всем этом вам помогут курсы профильной математики в онлайн-школе Skysmart. На них ребенок не только станет настоящим экспертом в точных науках, но и проведет время увлекательно и даже весело. Приходите вместе на бесплатный вводный урок и убедитесь сами!