Иррациональные уравнения

Определение иррациональных уравнений

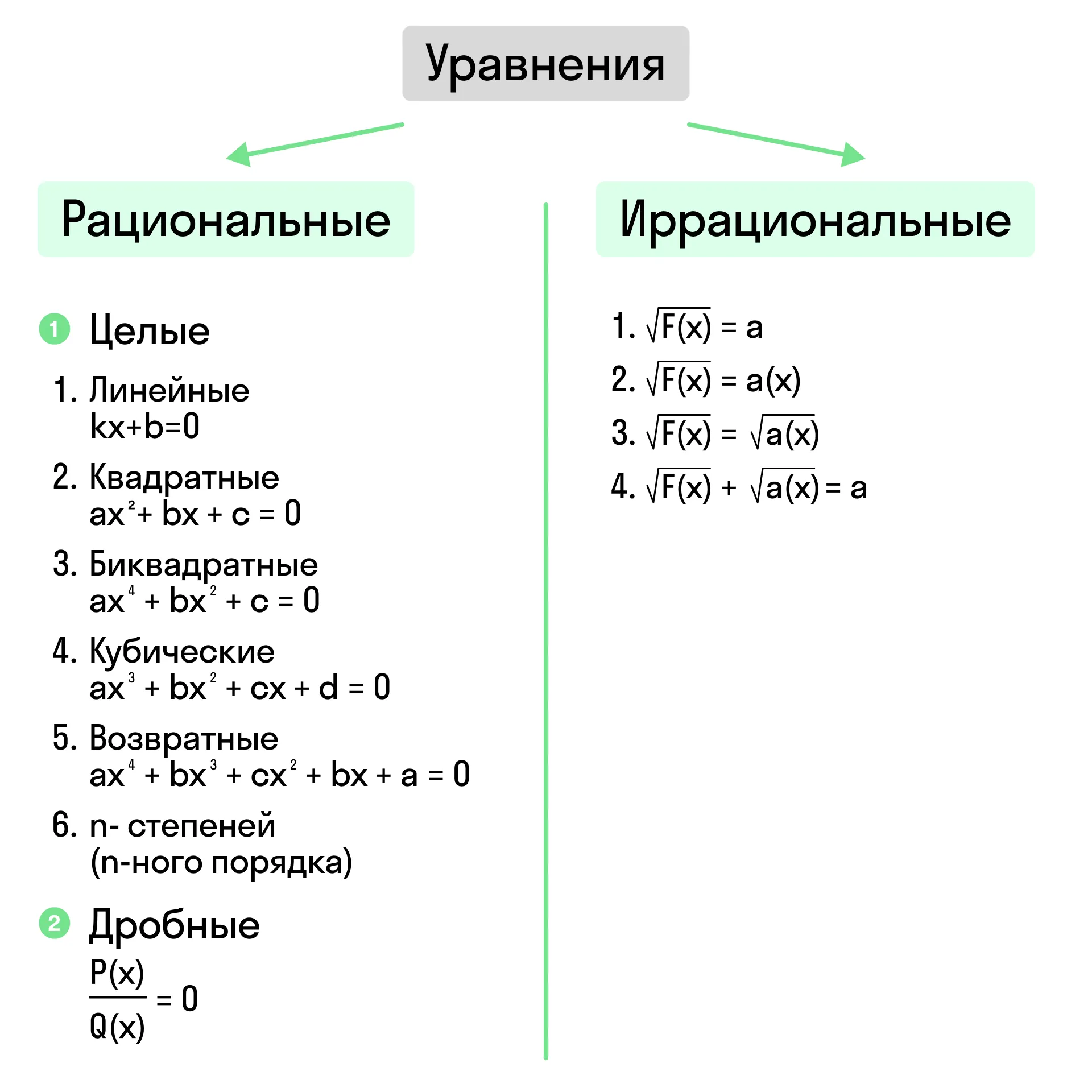
Иррациональные выражения — выражения, содержащие знак корня или степень, выраженную дробью.

Примеры: .

Для того, чтобы легко преобразовывать иррациональные выражения, важно знать:

1. Свойства корней:

   • Для любого числа a справедливо равенство:

   • Если , то

   • Если , то

   • Если , то

2. Область допустимых значений для корней чётной степени:

   для .

3. Свойство: корень n-ной степени может быть представлен в виде степени .

Иррациональные уравнения — уравнения, содержащие иррациональные выражения с неизвестной. Проще говоря, в уравнении неизвестная x будет стоять под знаком корня.

447.8K

Что такое квадратный кореньЧитать →

Типы иррациональных уравнений, алгоритмы и примеры решения

Первый тип иррациональных уравнений

Простейшее иррациональное уравнение выглядит так:

, где F(x) — выражение с переменной x, a — число.

Решаем такое уравнение по следующему алгоритму:

1. Обращаем внимание, корень какой степени представлен в уравнении: чётной или нечётной.

2. Оцениваем ОДЗ (область допустимых значений): для корней чётной степени и для корней нечётной степени.

3. Анализируем уравнение:

	корень чётной степени	уравнение не имеет решений
	корень нечётной степени	возводим обе части уравнения в степень корня и продолжаем решение.
	корень чётной степени
	корень нечётной степени

ОДЗ:

ОДЗ:

ОДЗ:

Второй тип иррациональных уравнений

, где F(x) и G(x) — выражения с переменной x.

Выражение под квадратным корнем равно выражению без корня. Что делать в таком случае?

1. Оцениваем ОДЗ выражения справа: . Оценивать подкоренное выражение не нужно, ведь если , то .

2. Возводим обе части в квадрат и продолжаем решение уравнения.

3. Анализируем корни: входят ли они в промежуток допустимых значений.

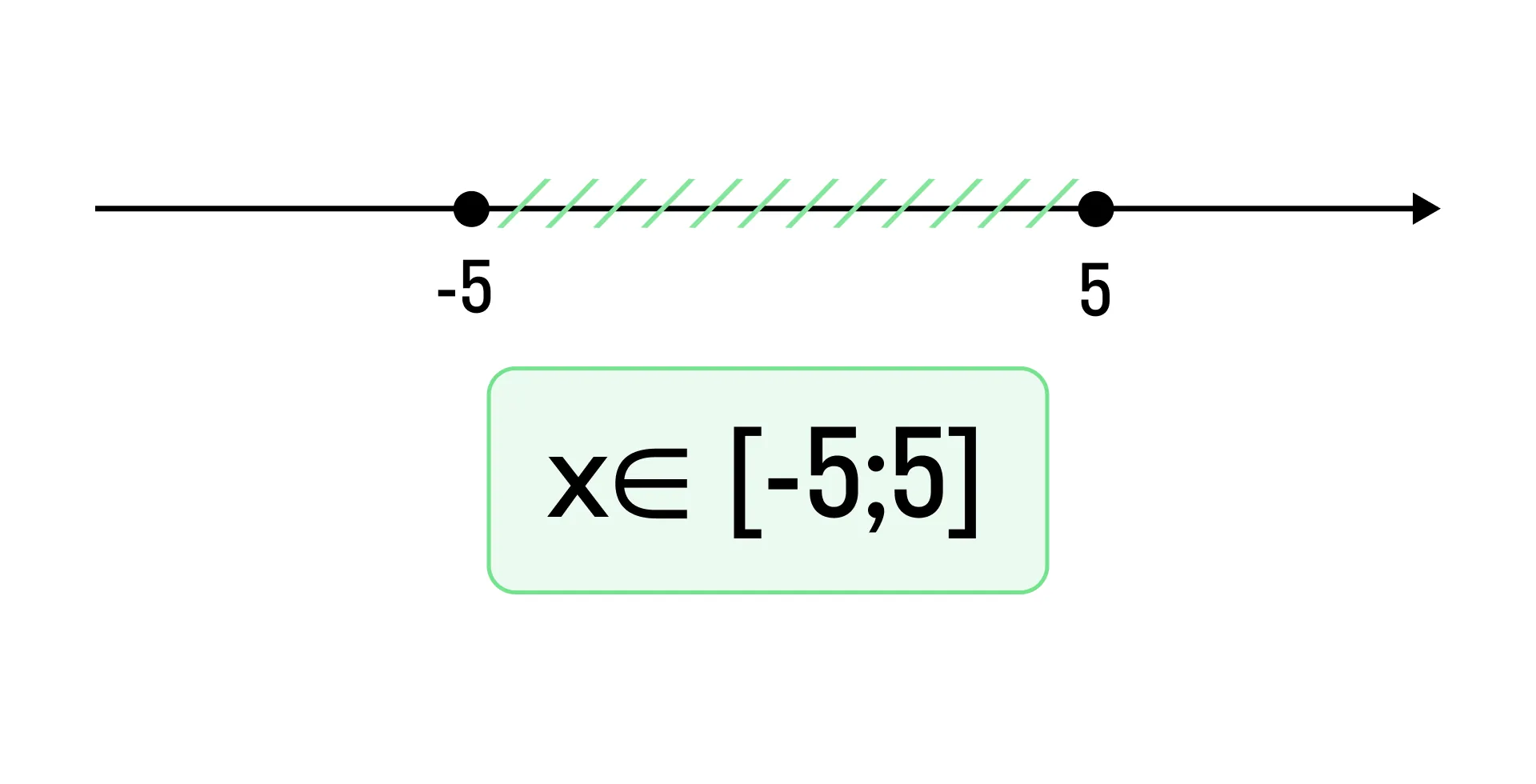
ОДЗ:

Корень x₂ = 6 не соответствует ОДЗ.

Ответ: x₁ = 9.

Третий тип иррациональных уравнений

, где F(x) и G(x) — выражения с переменной x.

Хотя тип уравнения отличается, действовать мы будем по уже известному алгоритму:

1. Оцениваем ОДЗ одного из выражений: или (эти условия равносильны, поэтому выбираем то выражение, чьё ОДЗ легче оценить).

2. Возводим обе части в квадрат и продолжаем решение уравнения.

3. Анализируем корни: входят ли они в промежуток допустимых значений.

ОДЗ:

Корень x₂ = −1 не соответствует ОДЗ.

Ответ: x₁ = 6.

Четвёртый тип иррациональных уравнений

, где F(x) и G(x) — выражения с переменной x, a — число.

Признайтесь, напугались? Да, неприятный тип, но не очень страшный.
Следуем алгоритму:

1. Оценим ОДЗ обоих подкоренных выражений:

2. Возведём обе части уравнения в квадрат и преобразуем, сводя к типу номер 2: F(x) = G(x).

3. Решим полученное уравнение.

ОДЗ:

Хотите попробовать решить иррациональное уравнение самостоятельно? Тогда переходите по ссылке и занимайтесь бесплатном тренажёре ЕГЭ от Skysmart. В нём вы найдете множество упражнений с автоматической проверкой, которые помогут вам закрепить пройденный материал и подготовиться к любого вида контрольным и экзаменам!