Что такое рациональные числа?

Определение рациональных чисел

Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Если число можно получить делением двух целых чисел, то это число рациональное.

Рациональные числа — это те, которые можно представить в виде

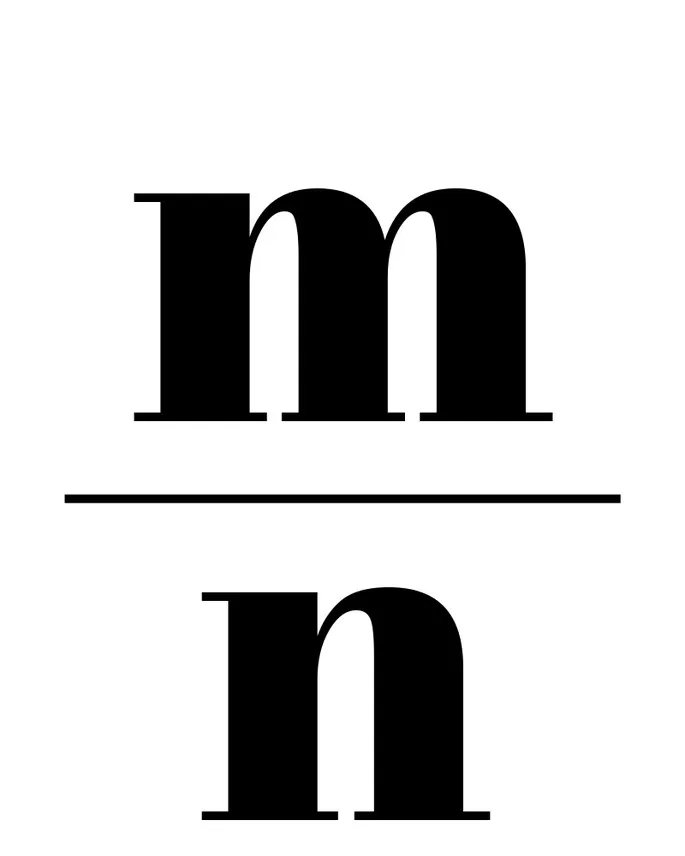
где числитель m — целое число, а знаменатель n — натуральное число.

Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.

Множество рациональных чисел принято обозначать латинской буквой Q.

Примеры рациональных чисел:

• десятичная дробь 1,15 — это 115/100;
• десятичная дробь 0,5 — это 1/2;
• целое число 0 — это 0/1;
• целое число 6 — это 6/1;
• целое число 1 — это 1/1;
• бесконечная периодическая дробь 0,33333... — это 1/3;
• смешанное число 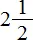— это 25/10;
• отрицательная десятичная дробь -3,16 — это -316/100.

 

Соглашаюсь на обработку персональных данных в соответствии с условиями пользовательского соглашения

← Далее →

Скачать

Modal window id: popup-professionsbox

Свойства рациональных чисел

У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.

Основные свойства действий с рациональными числами Переместительное свойство сложения: a + b = b + a. Сочетательное свойство сложения: (a + b) +c = a + (b + c). Сложение рационального числа и нейтрального элемента (нуля) не изменяет это число: a + 0 = a. У каждого рационального числа есть противоположное число, а их сумма всегда равна нулю: a + (-a) = 0. Переместительное свойство умножения: ab = ba. Сочетательное свойство умножения: (a * b) * c = a * (b * c). Произведение рационального числа и едины не изменяет это число: a * 1 = a. У каждого отличного от нуля рационального числа есть обратное число. Их произведение равно единице: a * a−1 = 1. Распределительное свойство умножения относительно сложения: a * (b + c) = a * b + a * c.

Кроме основных перечисленных есть еще ряд свойств:

 

1. Правило умножения рациональных чисел с разными знаками: (-a) * b = -ab. Такая фраза поможет запомнить: «плюс на минус есть минус, и минус на плюс есть минус».


2. Правило умножения отрицательных рациональных чисел: (−a) * (−b) = ab. Запомнить поможет фраза: «минус на минус есть плюс».


3. Правило умножении произвольного рационального числа на нуль: a * 0 = 0 или 0 * a = 0. Докажем это свойство.
   
   Мы знаем, что 0 = d + (-d) для любого рационального d, значит a * 0 = a * (d + (-d)).
   
   Распределительный закон позволяет переписать выражение:
   
   a * d + a * (−d), а так как a * (−d) = -ad, то a * d + a * (-d) = a * d + (-ad).
   
   Так получилась сумма двух противоположных чисел, которая в результате дает нуль, что доказывает равенство a * 0 = 0.

Мы перечислили только свойства сложения и умножения. На множестве рациональных чисел вычитание и деление можно записать, как обратные к сложению и умножению. То есть, разность (a - b) можно записать, как сумму a + (-b), а частное a/b равно произведению a * b−1, при b ≠ 0.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

170.4K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Прокачивай знания на курсах математики.

• Выбирай из 1200+ репетиторов по математике.

• Записывайся на бесплатные курсы для детей.

Определение иррационального числа

Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби

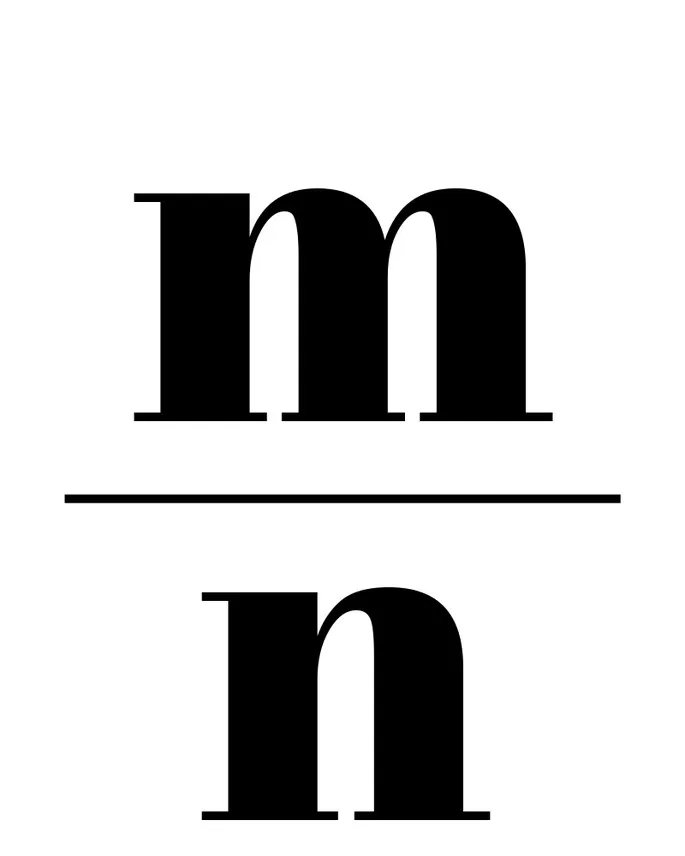
Оно может быть выражено в форме бесконечной непериодической десятичной дроби.

Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.

Примеры:

• π = 3,1415926...
• √2 = 1,41421356...
• e = 2,71828182…
• √8 = 2.828427...
• -√11= -3.31662…

Обозначение множества иррациональных чисел: латинская буква I.

Действительные или вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.

Свойства иррациональных чисел:

• результат суммы иррационального числа и рационального равен иррациональному числу;
• результат умножения иррационального числа на любое рациональное число (≠ 0) равен иррациональному числу;
• результат вычитания двух иррациональных чисел равен иррациональному числу или рациональному;
• результат суммы или произведения двух иррациональных чисел равен рациональному или иррациональному, например: √2 * √8 = √16 = 4).

Различие между целыми, натуральными и рациональными числами

Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое: один банан, две тетрадки, десять стульев.

А вот, что точно не является натуральным числом:

• Нуль — целое число, которое при сложении или вычитании с любыми числами в результате даст то же число. Умножение на ноль дает ноль.
• Отрицательные числа: -1, -2, -3, -4.
• Дроби: 1/2, 3/4, 5/6.

Целые числа — это натуральные числа, противоположные им и нуль.

Если два числа отличаются друг от друга знаком — их называют противоположными: +2 и -2, +7 и -7. Знак «плюс» обычно не пишут, и если перед числом нет никакого знака, значит оно положительное. Числа, перед которыми стоит знак «минус», называют отрицательными.

Какие числа называются рациональными мы уже знаем из первой части статьи. Повторим еще раз.

Рациональные числа — это конечные дроби и бесконечные периодические дроби.

Например: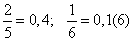

Любое рациональное число можно представить в виде дроби, у которой числитель принадлежит целым числам, а знаменатель — натуральным. Поэтому во множество рациональных чисел входит множество целых и натуральных чисел.

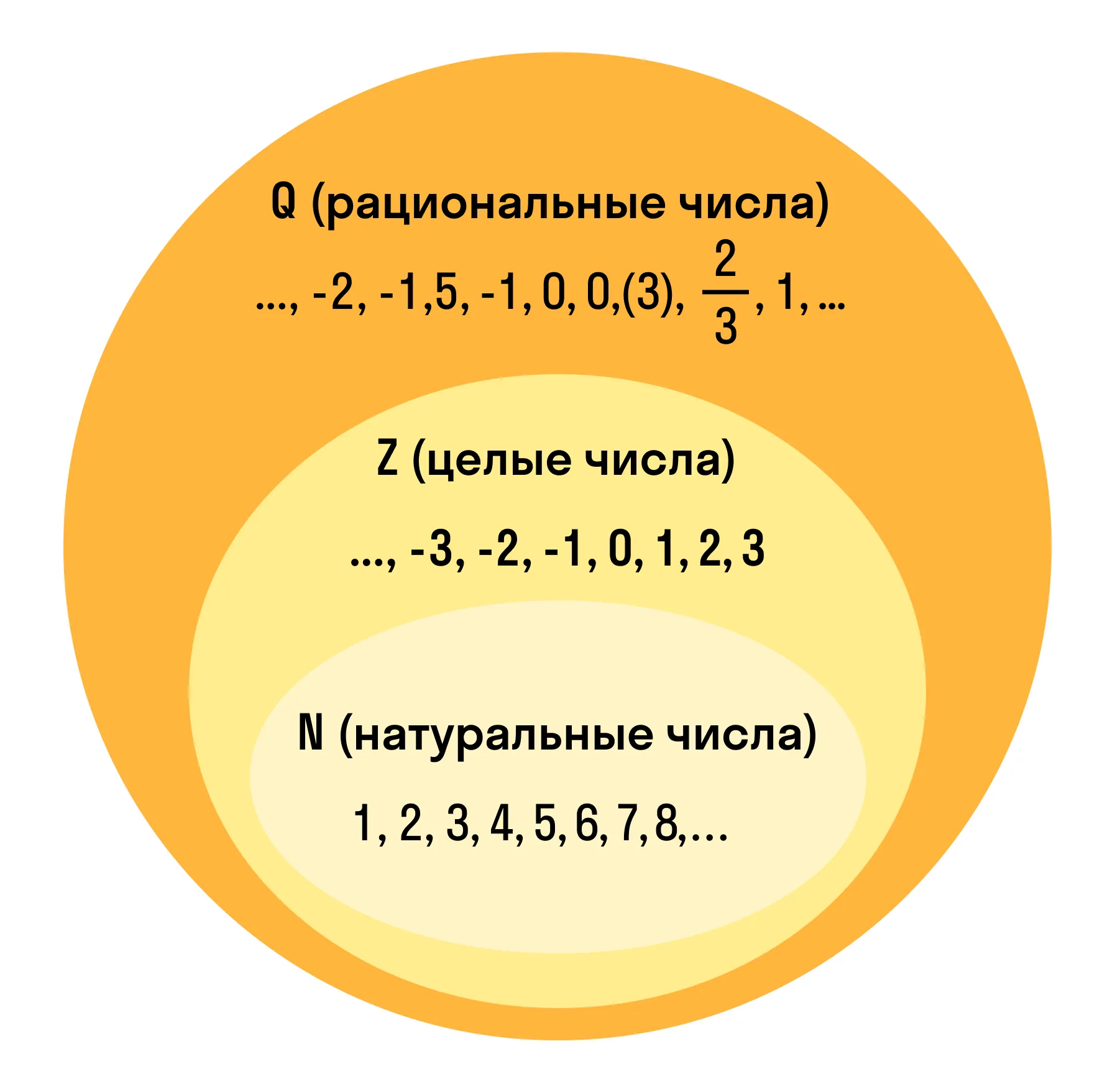
Но не все числа можно назвать рациональными. Например, бесконечные непериодические дроби не принадлежат множеству рациональных чисел. Так √3 или 𝜋 (число пи) нельзя назвать рациональными числами.