Решение задач с параметром

Что такое параметр

Параметр — это буквенный коэффициент в уравнении. Чаще всего его обозначают буквой a.

Уравнения с параметром — это уравнения, в которых помимо неизвестной переменной есть ещё один буквенный коэффициент.

Например, в уравнении , a — параметр. Его точное значение определить невозможно: оно зависит от условия задачи, и в некоторых случаях подходит не одно, а целое множество значений.

Из алгебры мы знаем, что для решения уравнений с двумя неизвестными необходимо иметь как минимум два уравнения (систему). В решении уравнений с параметром такая система отсутствует, но нам и не нужно определять точное значение x. Мы будем анализировать количество корней уравнения и их зависимость от параметра.

Рассмотрим пример того, как это работает. Решим уравнение и порассуждаем, как от значения параметра a зависит значение переменной x.

Задача 1

если , то	если , то уравнение не имеет решения, так как делить на ноль нельзя	если , то

Параметр можно использовать в уравнении любого типа: рациональном и иррациональном, тригонометрическом, логарифмическом и т. д.

Уравнения с параметром решаются разными методами:

1. Алгебраическим — путём непосредственного решения уравнения и анализа полученных корней относительно параметра а.

2. Графическим — через введение функции и построения её графика.

В этой статье мы будем использовать алгебраический метод решения уравнений с параметром.

Вне зависимости от типа уравнения мы всегда будем придерживаться следующего алгоритма:

1. Оценим ОДЗ (если необходимо).

2. Преобразуем уравнение таким образом, чтобы выразить неизвестную x. На параметр как будто не обращаем внимания, считаем его второстепенным коэффициентом: поступаем с ним так же, как с другими свободными членами уравнения.

3. Проанализируем полученное выражение и ответим на вопрос по заданию.

Линейное уравнение с параметром

Общий вид линейного уравнения: , a и b — какие-то числа.

В линейном уравнении с параметром чаще всего вместо b стоит число, а коэффициент а остаётся. Тогда возможны следующие развития событий:

• если , решений у уравнения нет,

• если , то ,

• если и , то уравнение имеет множество решений.

Задача 2

Решите уравнение с учётом всех значений параметра k: .

Решение:

1. Выразим неизвестную переменную х через параметр k.

2. Проанализируем результаты через значения параметра. На параметр не распространяются никакие ограничения, он может быть как отрицательным, так и положительным. Поэтому решение справедливо для любого значения k.

150.4K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Квадратное уравнение с параметром

Общий вид квадратного уравнения: , a, b, c — какие-то числа, при этом коэффициент а называют старшим, b — средним коэффициентом, c — свободным членом.

Параметр может стоять на месте любого из коэффициентов.

Рассмотрим типовые задания на квадратное уравнение с параметром.

Задача 3

Найдите все значения параметра а, при которых уравнение имеет два корня.

Решение:

1. Для решения квадратных уравнений используют множество методов, в том числе через дискриминант. Вспомним, как значение дискриминанта влияет на количество корней уравнения:

• , уравнение имеет 2 корня;

• , уравнение имеет 1 корень;

• , уравнение не имеет корней.

2. Соответственно, чтобы определить, при каких значениях параметра а уравнение не имеет корней, нужно составить формулу дискриминанта и оценить, когда D будет больше нуля.

3. Определим коэффициенты в уравнении:

   a (в значении старшего коэффициента) = 1

4. Составим формулу для дискриминанта:

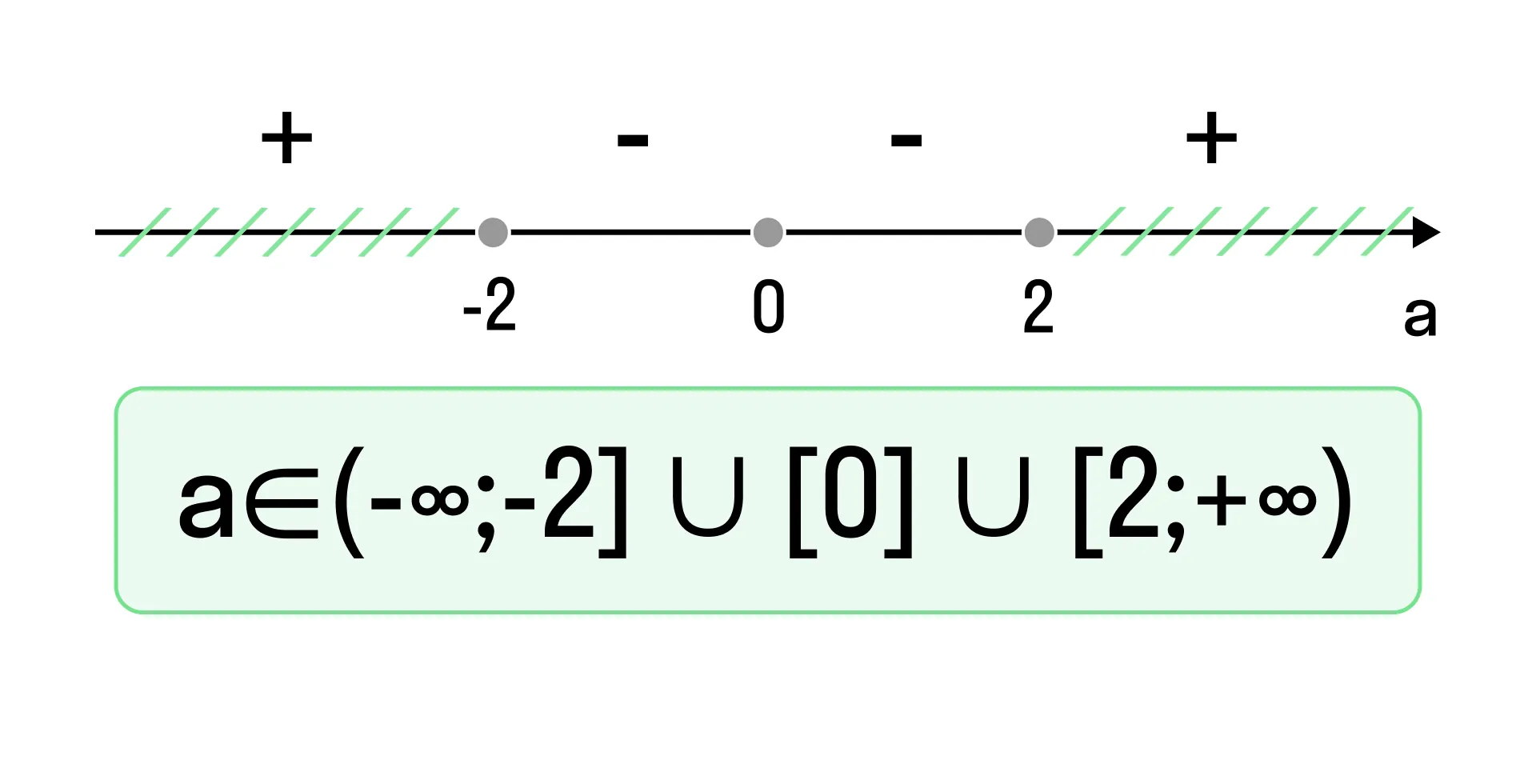
5. Составим неравенство и оценим значение параметра a:

   

Ответ: уравнение имеет два корня при .

Задача 4

При каких значениях параметра a уравнение имеет менее двух корней?

Решение:

1. Обращаем внимание на то, что параметр а входит в состав старшего коэффициента, который не может быть равен нулю необходимо оценить ОДЗ для параметра:

2. Фраза «менее двух корней» подразумевает, что у уравнения может быть один корень или ноль корней. А значит, дискриминант должен быть меньше или равен нулю.

3. Оценим значение коэффициентов квадратного уравнения и составим дискриминант:

   (в значении старшего коэффициента)

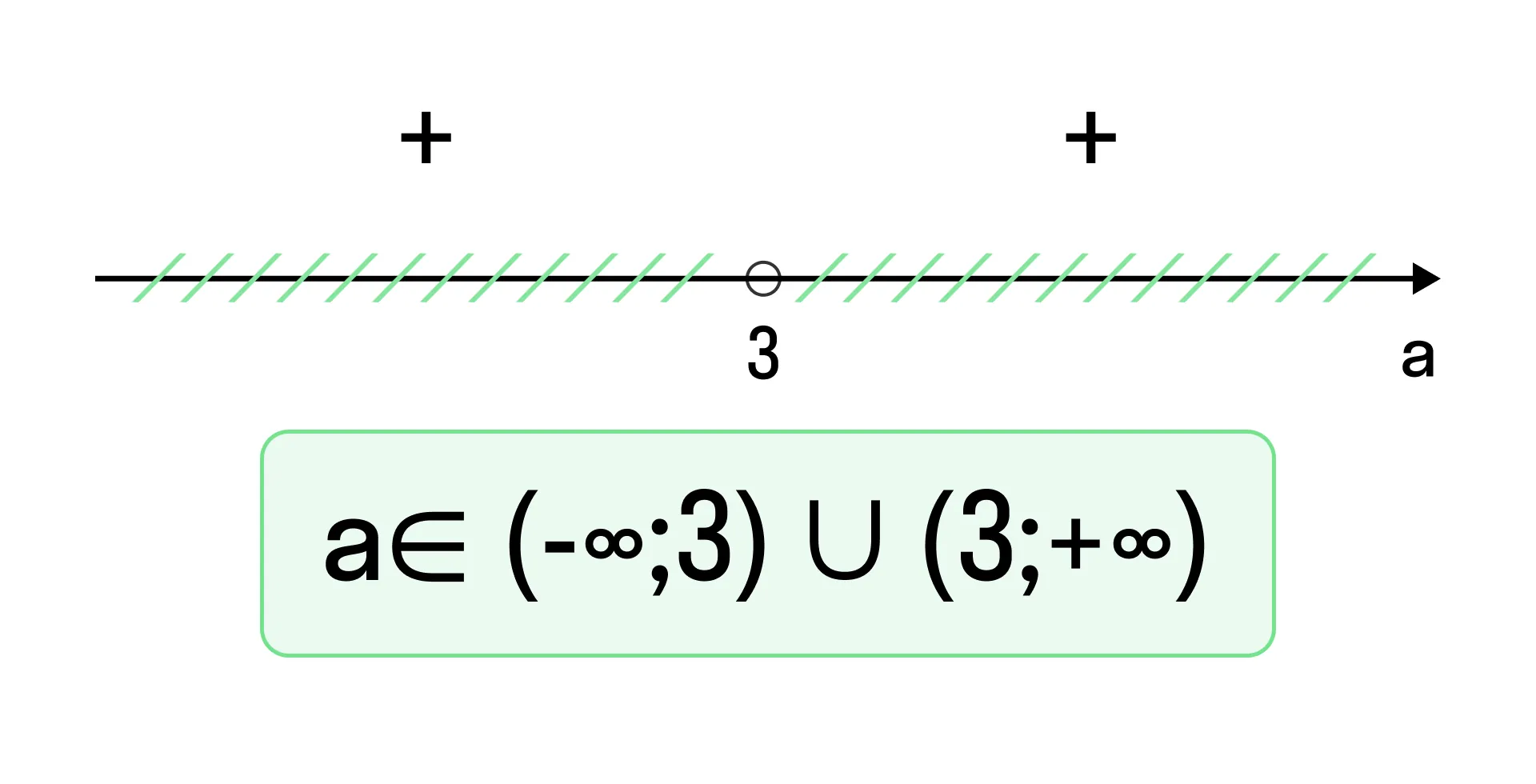
4. Составим неравенство, исходя из рассуждений в пункте 2:

   

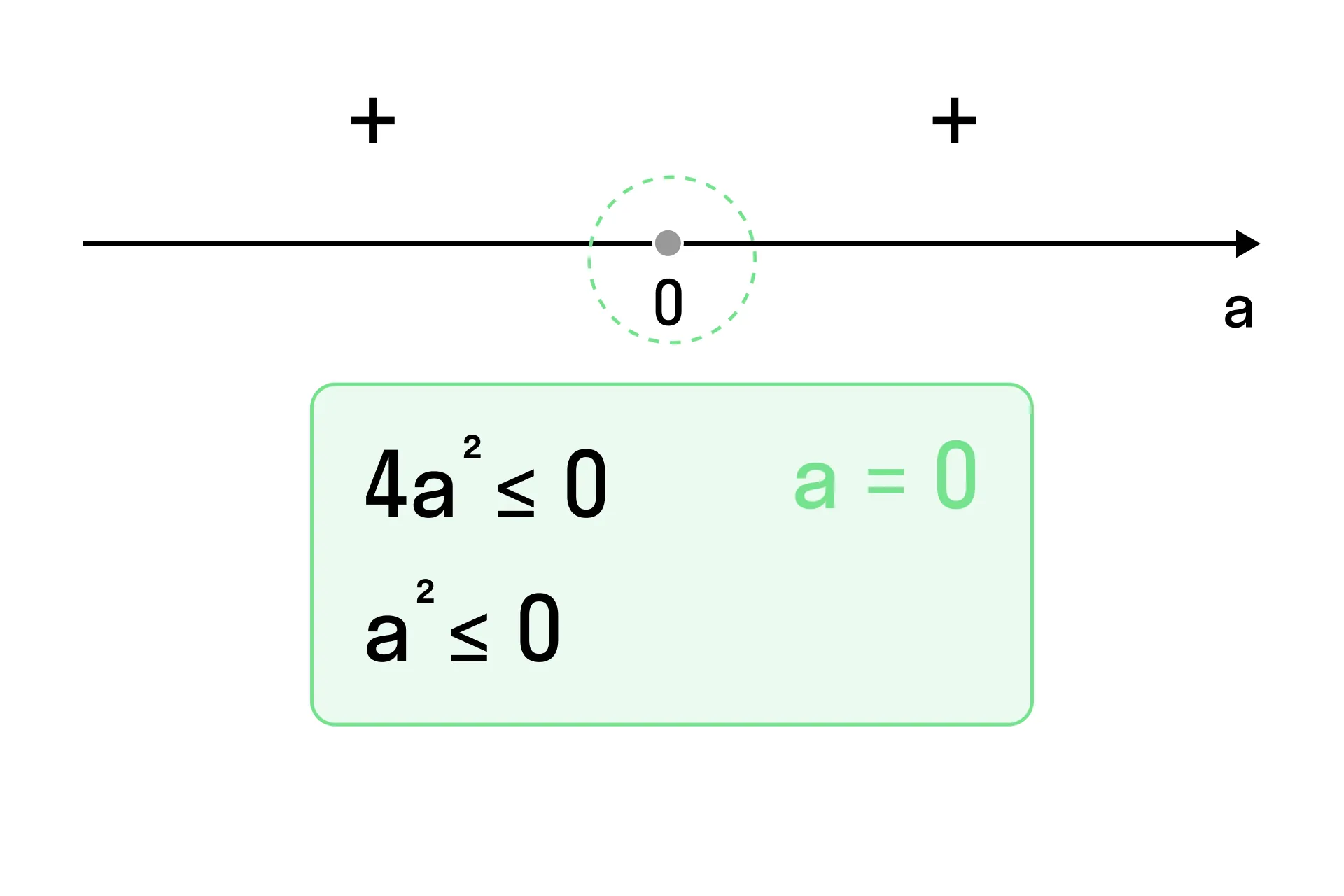
5. Сделаем проверку. Подставим полученное значение параметра а и решим уравнение:

Вывод: при а = 0 уравнение имеет менее двух корней.

Иррациональные уравнения с параметром

Решение иррациональных уравнений с параметром может быть проще, если следовать этим советам:

1. Постарайтесь выделить корень с одной стороны уравнения.

2. Чтобы убрать корень, возведите обе стороны уравнения в квадрат (после оценки ОДЗ). Если уравнение содержит несколько корней, повторите этот шаг.

3. Убедитесь, что найденные решения подходят для исходного уравнения и удовлетворяют всем ограничениям.

4. Для сложных уравнений постройте графики функций, чтобы найти пересечения и решения.

5. Проверьте все решения, убедитесь, что все найденные корни удовлетворяют исходному уравнению.

Задача 5

Найдите все значения параметра a, при которых уравнение имеет один корень.

Решение:

1. Оценим ОДЗ (достаточно проанализировать область допустимых значений одного из подкоренных выражений):

2. Возведём обе части уравнения в квадрат:

3. Найдем корни уравнения через дискриминант (проанализируем вариант при ):

4. Проверим, при каких значениях параметра a эти корни соответствуют ОДЗ. Для этого подставим оба значения в неравенство :

Проверяем

Проверяем т. е. значение является корнем уравнения при любых значениях а.

Т. е. оба варианта соответствуют ОДЗ.

1. Согласно условию задачи, нам нужно найти значения параметра а, при которых уравнение имеет один корень. Сейчас у нас получилось два корня, но что, если они могут совпадать друг с другом? Оценим, при каких значениях параметра а :

Делаем вывод: у уравнения может быть один корень, если:

1. (при ),

2. если корень x₁ не соответствует ОДЗ (при ).

Ответ: .

Тригонометрические уравнения с параметром

Для решения тригонометрических уравнений с параметром мы будем придерживаться тех же принципов, что и в других уравнениях: оценивать ОДЗ и выражать неизвестную x, а далее оценивать полученные результаты.

Вот общие советы для решения подобных уравнений:

1. Разберитесь, какие тригонометрические функции используются (синус, косинус, тангенс и т. д.).

2. Упростите уравнение, используя тригонометрические тождества.

3. Попробуйте выразить уравнение через параметр, если это возможно.

4. Посмотрите, как разные значения параметра влияют на решение уравнения.

5. Найдите общее решение уравнения с параметром, используя известные методы.

6. Постройте графики функции и параметра, чтобы увидеть, при каких значениях параметра уравнение имеет решения.

7. Учитывайте периодичность тригонометрических функций и проверяйте все возможные значения.

8. Учитывайте ограничения: параметры могут изменять область допустимых значений функции.

Задача 6

Решите уравнение с учётом всех значений параметра a:

Решение:

ОДЗ:

1. Оценим правую часть уравнения согласно ОДЗ (вначале используем условия меньше единицы, затем – равно единице)

   Тогда

2. если а = 0, то

   если а = 2, то

3. Вне пределов ОДЗ (если или ) уравнение не имеет решений.

Ответ:

• при

• при ,

• при ,

• при или уравнение не имеет решения.

Задача 7

Решите уравнение с учётом всех значений параметра a:

Решение:

Вынесем за скобки:

Настало время оценить ОДЗ. Помним, что область значений синуса — промежуток [−1; 1].

Тогда

Найдём значение переменной x:

Решая уравнения с параметром, воспользуйтесь нашей памяткой — она позволит вам проанализировать задание и выбрать наиболее рациональный способ решения.

Как начать решение задачи?

1. Определите тип уравнения (линейное, квадратное, рациональное и т. д.).

2. Определите, что нужно найти: решение уравнения или количество его корней.

3. Определите ключевые параметры, если это возможно. Например, для квадратных уравнений важно учитывать старший коэффициент и дискриминант.

4. Проанализируйте, влияет ли нахождение области допустимых значений переменной на параметры.

5. Попробуйте поменять переменную и параметр местами. Возможно, это упростит задачу. Например, уравнение может быть квадратным относительно переменной и линейным относительно параметра.

Хотите улучшить свои навыки и уверенность в решении задач с параметром? Попробуйте бесплатный тренажёр ЕГЭ! Это отличная возможность потренироваться и закрепить изученный материал в удобном формате. Зайдите и убедитесь сами — это легко и доступно. Удачи в обучении!