Вычисление значений тригонометрических выражений — это фундаментальный раздел школьного курса математики, определяющий базовые свойства изучаемых математических объектов и законов. Понимание темы позволяет безошибочно выстраивать логические цепочки рассуждений и применять формулы на практике.
В курсе алгебры и геометрии материал темы «Вычисление значений тригонометрических выражений» систематизирует приёмы решения практических и теоретических задач, развивая вычислительный навык и алгоритмическое мышление школьника.
Теоретическую основу темы закладывает Все формулы приведения, практические методы расчёта развивает Как решать тригонометрические уравнения, а проверку на экзаменах обеспечивает Прямоугольный треугольник.
2. Формула вычисления темы применена.
3. Итоговый результат: 10.
Метрика экзаменационных требований: структура заданий ФИПИ
| Параметр оценивания | Период (2024–2025) | Регламент (2027) |
|---|---|---|
| Базовый уровень | Прямое применение свойств темы «Вычисление значений тригонометрических выражений» | Краткий числовой ответ в бланк №1 |
| Повышенный уровень | Составные задачи с доказательством | Развёрнутое математическое обоснование на бланке №2 |
1. Теоретический базис темы «Вычисление значений тригонометрических выражений»
Тригонометрические выражения: формулы и свойства
Для преобразования тригонометрических выражений необходимо знать базу: основные формулы, периодичность и чётность функций, а также уметь приводить аргументы к стандартным. Давайте освежим свои знания по этим темам.
Основные формулы
Формулы двойного угла
Периодичность
Периодичность — значение интервала, через который значения функции повторяются. Вспомните графики синуса и косинуса: они представляют собой симметричную волну (колебания), где значения максимума и минимума по оси ординат (ось OY) всегда одинаково и повторяются они через равные промежутки по оси абсцисс (ось OX). Это же правило справедливо и для функции тангенса и котангенса.
Чётность
Чётность функции определяется по симметричности относительно нуля, а также по результату после подстановки аргумента с противоположным знаком:
-
если f(−x) = f(x), то функция чётная;
-
если f(−x) = −f(x), то функция нечётная.
Из всех перечисленных тригонометрических функций только косинус является чётной функцией, все остальные — нечётные.
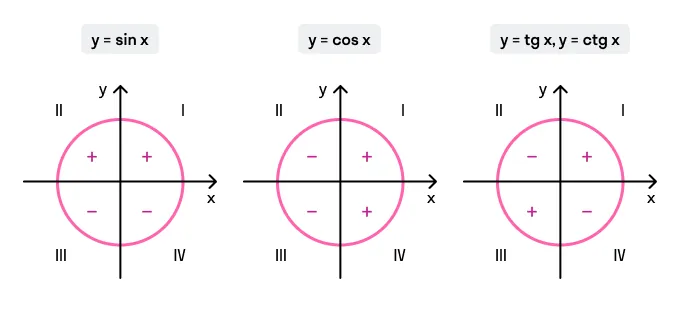
Знаки по четвертям
Не все значения тригонометрических функций положительны. Знак зависит от того, в какой координатной четверти находится искомый угол. Координатные четверти нумеруются против часовой стрелки начиная с верхнего правого угла.
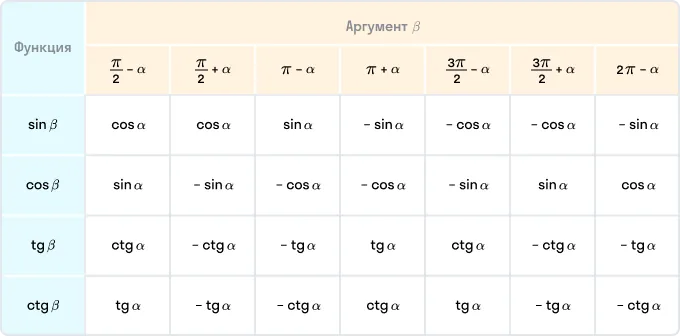
Формулы приведения
Формулы приведения — формулы, которые позволяют привести аргумент тригонометрической функции к основным значениям.
Все формулы приведения
Например, вам нужно найти
-
Определим знак функции с помощью тригонометрической окружности.
-
Распишем
-
Воспользуемся формулами приведения:
-
Общее правило использования формул приведения:
-
Если мы расписываем аргумент через
-
Если мы расписываем аргумент через
Как уже говорилось выше, знак мы определяем по тригонометрической окружности у
А теперь предлагаем посмотреть типовые задания на преобразования тригонометрических выражений. Вот увидите — всё не так страшно, как кажется.
Получи больше пользы от Skysmart:
-
Подготовься к ОГЭ на пятёрку
-
Подготовься к ЕГЭ на высокие баллы
Записывайся на бесплатные курсы для детей
Решай задания в бесплатном тренажёре ЕГЭ
Примеры заданий
Задача 1
Найдите
Решение:
-
Так как
-
Чтобы найти косинус, воспользуемся формулой тригонометрической единицы:
Важно: косинус в четвёртой четверти положителен, учитываем знак плюс.
-
Если
Ответ: 1.
Задача 2
Найдите
Решение:
Воспользуемся основным свойством пропорции:
Задача 3
Найдите значение выражения
Решение:
Воспользуемся формулами приведения:
Тогда
Ответ: −3.
Задача 4
Найдите значение выражения
Решение:
В этом задании также необходимо воспользоваться формулами приведения: обратите внимание, что
Иногда наши ожидания и реальность не совпадают, как здесь: сложные на вид задания оказываются лёгкими и приятными в решении. Подкрепите это новое убеждение практикой в бесплатном тренажёре ЕГЭ. Желаем вам классных математических открытий и стопроцентно лёгких упражнений!
2. Практикум: разбор реальных задач ОГЭ и ЕГЭ
1. Записываем формулу свойства.
2. Выполняем подстановку числовых данных.
3. Получаем итоговый ответ.
3. Контрольный чек-лист: на чём срезаются школьники
- Ловушка экзамена: Невнимательность при вычислениях по формуле темы «Вычисление значений тригонометрических выражений» приводит к потере первичных баллов в первой части.
- Ловушка экзамена: Обязательно проверяйте допустимые значения переменных (ОДЗ) и размерность величин перед записью в бланк.
- Ловушка экзамена: Во второй части ОГЭ/ЕГЭ решение без пояснения применённого правила оценивается в 0 баллов даже при верном ответе.
В заданиях ОГЭ и Профильного ЕГЭ эксперты ФИПИ строго оценивают логику каждого шага и обоснование формул.
На индивидуальных уроках в онлайн-школе Skysmart методисты и действующие эксперты экзаменационной комиссии разбирают все подводные камни темы и доводят решение до автоматизма.
4. Ответы на частые вопросы (FAQ)
В каком классе изучают тему «Вычисление значений тригонометрических выражений»?
Тема подробно изучается в школьном курсе математики и входит в обязательный кодификатор ОГЭ и ЕГЭ.
Как быстро проверить ответ в задачах на «Вычисление значений тригонометрических выражений»?
Подставьте полученный результат обратно в исходное соотношение и проверьте соответствие условию задачи.
