Как найти дискриминант квадратного уравнения? Онлайн-калькулятор

Калькулятор дискриминанта квадратного уравнения

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, содержащее переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим:

• 5 + 8 = 12;

• 13 = 12 — противоречие.

Значит, х = 5 не является корнем уравнения.

Если же х = 4, то при подстановке в уравнение мы получим:

• 5 + 8 = 12;

• 12 = 12 — верное равенство.

Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.

Например

• 2x² − x + 5 = 0

• a = 2, b = −1, c = 5

Такое уравнение можно решить с помощью формулы дискриминанта.

220.7K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Прокачивай знания на курсах математики

• Выбирай из 1200+ репетиторов по математике

• Записывайся на бесплатные курсы для детей

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, равное b² − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Как решать квадратные уравнения через дискриминант

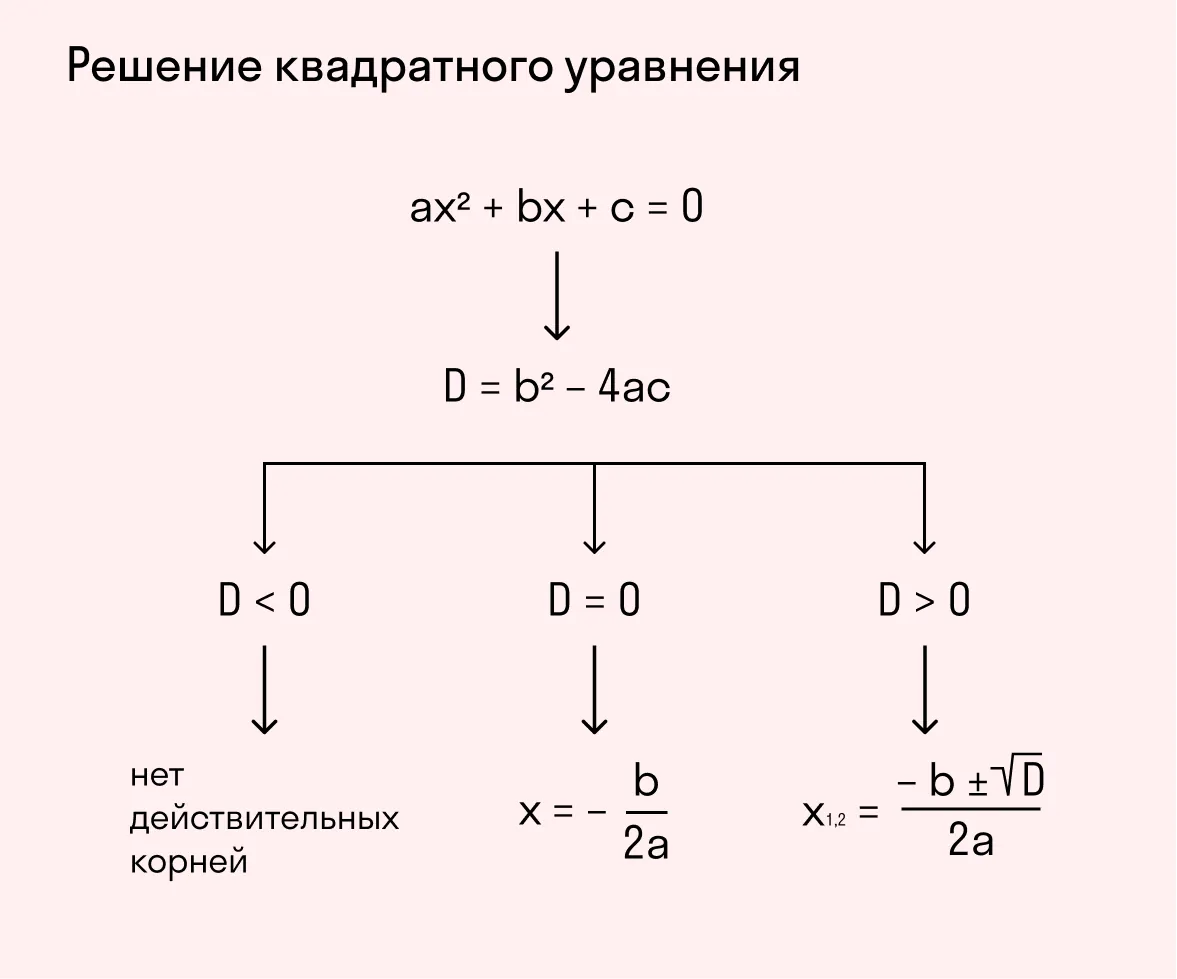
Алгоритм решения квадратного уравнения ax² + bx + c = 0:

1. Определим, чему равны коэффициенты a, b, c.

2. Вычислим значение дискриминанта по формуле D = b2 − 4ac.

3. Если дискриминант D < 0, то корней нет.

   Если D = 0, то есть один корень, равный −b/2a.

   Если D > 0, то у уравнения две корня, равные

Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:

Примеры решения квадратных уравнений с помощью дискриминанта

Пример 1. Решить уравнение: 3x² - 4x + 2 = 0.

Как решаем:

1. Определим коэффициенты: a = 3, b = -4, c = 2.


2. Найдем дискриминант: D = b² - 4ac = (-4)² - 4 * 3 * 2 = 16 - 24 = -8.

Ответ: D < 0, корней нет.

Пример 2. Решить уравнение: x² - 6x + 9 = 0.

Как решаем:

1. Определим коэффициенты: a = 1, b = -6, c = 9.


2. Найдем дискриминант: D = b² - 4ac = (-6)² - 4 * 1 * 9 = 36 - 36 = 0.



3. D = 0, значит уравнение имеет один корень:

   

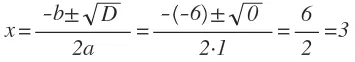
Ответ: корень уравнения 3.

Пример 3. Решить уравнение: x² - 4x - 5 = 0.

Как решаем:

1. Определим коэффициенты: a = 1, b = -4, c = -5.


2. Найдем дискриминант: D = b² - 4ac = (-4)² - 4 * 1 * (-5) = 16 + 20 = 36.



3. D > 0, значит уравнение имеет два корня:

   

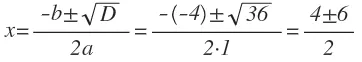
x₁ = (4 + 6) : 2 = 5,

x₂ = (4 - 6) : 2 = -1.

Ответ: два корня x₁ = 5, x₂ = -1.

Тест: Дискриминант квадратного уравнения

Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.