Основное тригонометрическое тождество - это уравнение, выражающее взаимосвязь между квадратами синуса и косинуса одного и того же угла:
sin²(x) + cos²(x) = 1
Примеры:
- Для угла 45°:
- sin(45°) = cos(45°) ≈ 0.707
- 0.707² + 0.707² ≈ 1
Для кого эта статья:
- Студенты и школьники, изучающие математику
- Преподаватели по математике
- Лица, интересующиеся тригонометрией
Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
|
sin2α + cos2α = 1 |
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg2α + 1 = 1/cos2α и равенство 1 + сtg2α + 1 = 1/sin2α выводят из основного тождества, разделив обе части на sin2α и cos2α.
В результате деления получаем:
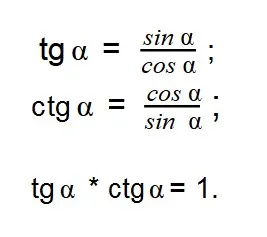
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin2α + cos2α = 1Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
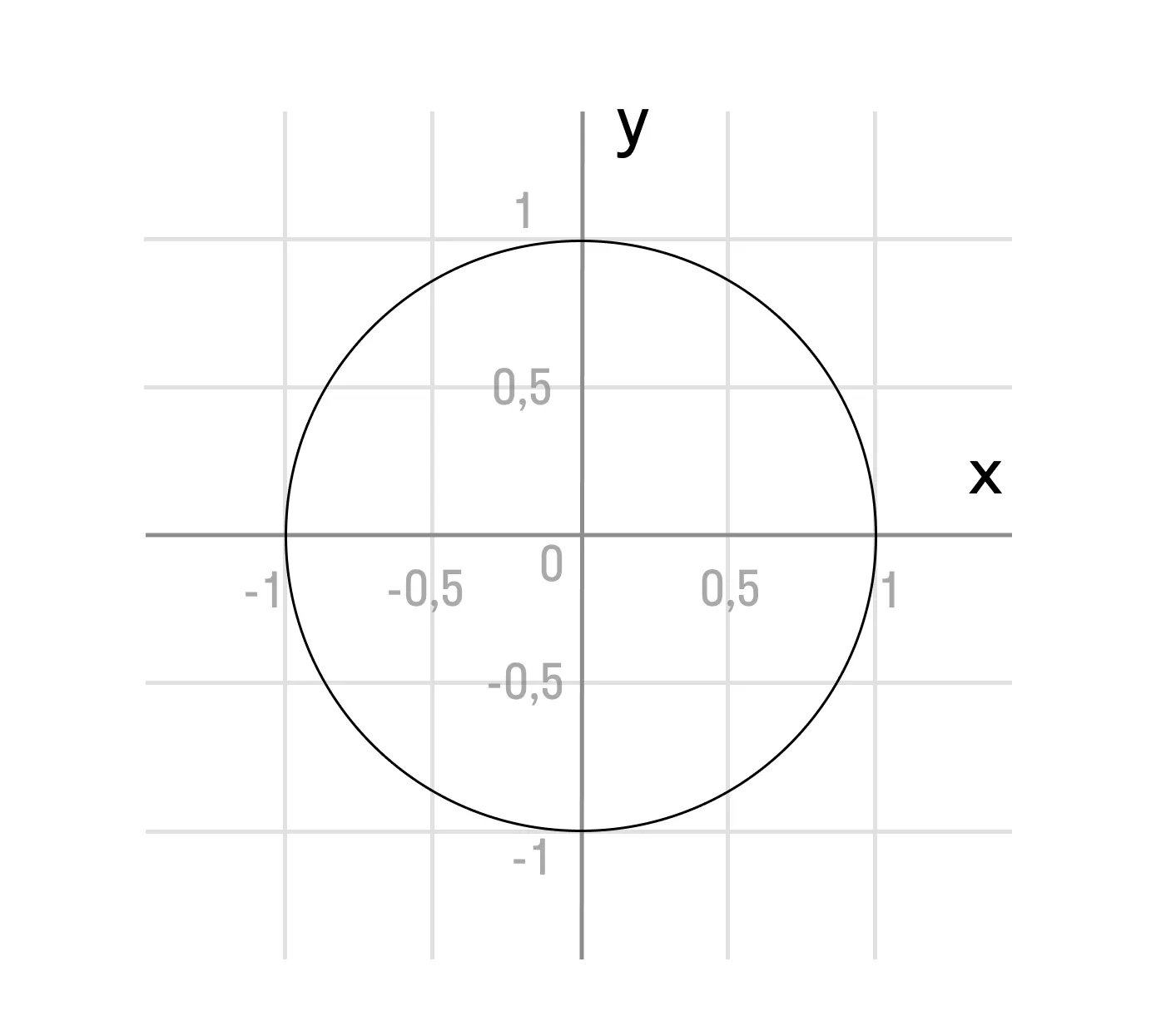
Докажем тождество sin2α + cos2α = 1
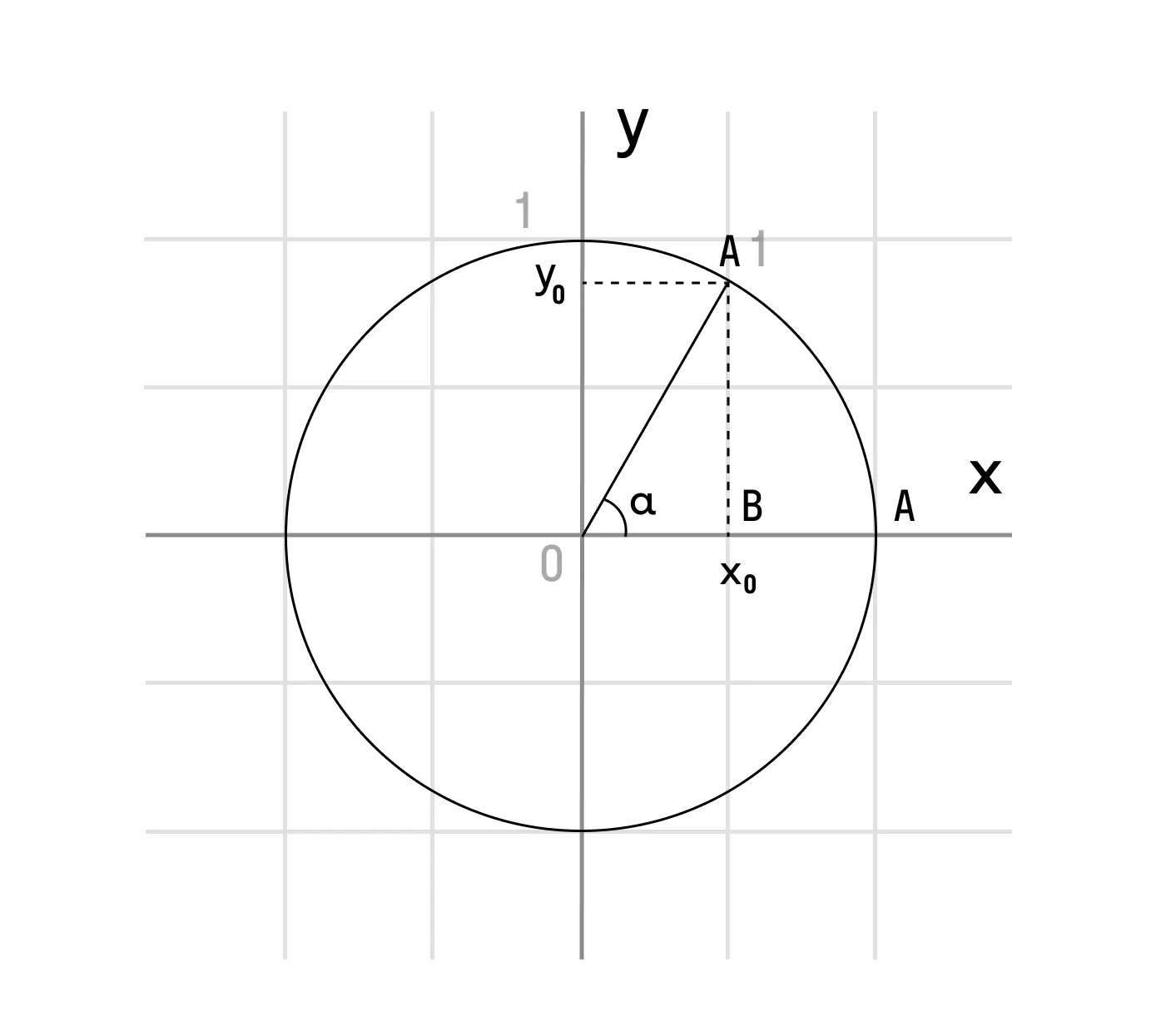
- Итак, нам известны координаты точки A (1; 0).
Произвольный угол α, тогда cos α = x0 = ОB. - Если развернуть точку A на угол α, то точка A становится на место точки A1.
- По определениям:
- Синус угла (sin α) — это отношение противолежащего катета к гипотенузе.
- Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.
- Опускаем перпендикулярную прямую A1B на x0 из точки A1.
Образовался прямоугольный треугольник OA1B.
|A1B| = |у|
|OB| = |x|. - Гипотенуза OA1 имеет значение, равное радиусу единичной окружности.
|OA1| = 1. - Применяя полученное выражение, записываем равенство по теореме Пифагора, поскольку получившийся угол — прямой:
|A1B|2 + |OB|2 = |OA1|2. - Записываем в виде: |y|2 + |x|2 = 12.
Это значит, что y2 + x2 = 1.
sin угла α = y
cos угла α = x - Вставляем данные угла вместо координат точек:
OB = cos α
A1B = sin α
A1O = 1 - Получаем основное тригонометрическое тождество: sin2α + cos2α = 1.
Что и требовалось доказать.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
- sin α = ±
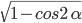
- cos α = ±
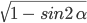
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.

Тангенс и котангенс через синус и косинус
Немного вводных:
- Синус угла — это ордината y.
- Косинус угла — это абсцисса x.
- Тангенс угла — это отношение ординаты к абсциссе.
- Котангенс угла — это отношение абсциссы к ординате.
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
- tg α =
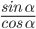
- ctg α =
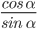
Исходя из определений:
- tg α =
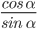 =
= 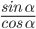
- ctg α =
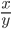 =
= 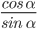
Это позволяет сделать вывод, что тригонометрические тождества
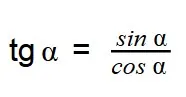
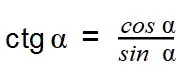
задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества
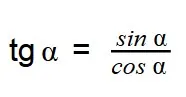
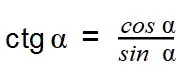
верны для всех углов α, значения которых вписываются в диапазон.
- Например, выражение
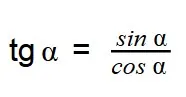 применимо для любого угла α, не равного
применимо для любого угла α, не равного 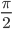 + π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.
+ π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.
Выражение
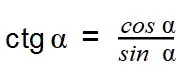
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Получи больше пользы от Skysmart:
-
Подготовься к ОГЭ на пятёрку
-
Подготовься к ЕГЭ на высокие баллы
Записывайся на бесплатные курсы для детей
Решай задания в бесплатном тренажёре ЕГЭ
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
- Тождество записывается в следующем виде:
tg α * ctg α = 1.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
- По определению:
tg α = y/x
ctg α = x/y - Отсюда следует, что tg α * ctg α = y/x * x/y = 1
- Преобразовываем выражение, подставляем
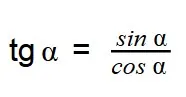 и
и 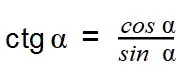 ,
,
получаем: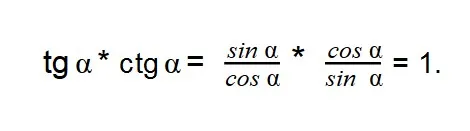
Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
- tg2α + 1 =
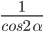
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
- 1 + ctg2α =
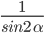
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin2α + cos2α = 1.
- Для этого нужно поделить обе части тождества на cos2α, где косинус не равен нулю.
- В результате деления получаем формулу tg2α + 1 =
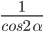
- Если обе части основного тригонометрического тождества sin2α + cos2α = 1 разделить на sin2α, где синус не равен нулю, то получим тождество:
1 + ctg2α =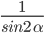 .
. - Отсюда можно сделать вывод, что тригонометрическое тождество tg2α + 1 =
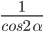 применимо для любого угла α, не равного
применимо для любого угла α, не равного 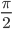 + π + z, где z — это любое целое число.
+ π + z, где z — это любое целое число. - А тригонометрическое тождество 1 + ctg2α =
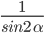 применимо для любого угла, не равного π * z, где z — это любое целое число.
применимо для любого угла, не равного π * z, где z — это любое целое число.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
|
1 |
sin2α + cos2α = 1 |
|
2 |
|
|
3 |
|
|
4 |
tgα * ctgα = 1 |
|
5 |
tg2α + 1 = |
|
6 |
1 + ctg2α = |
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
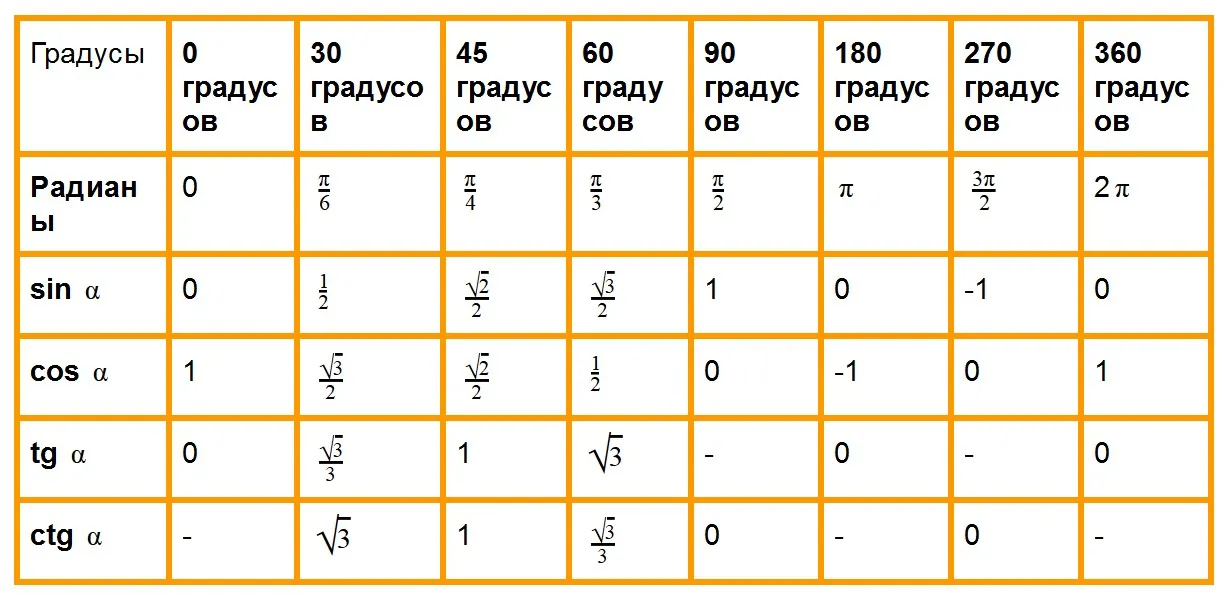
Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
Как решаем:
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
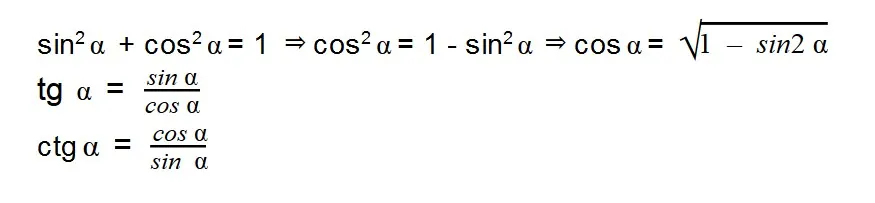
- Выражаем cos α из тригонометрической единицы:
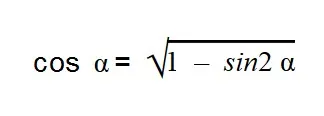
- Далее подставляем значения sin α:
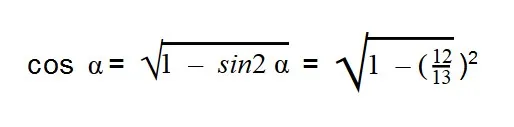
- Вычисляем:
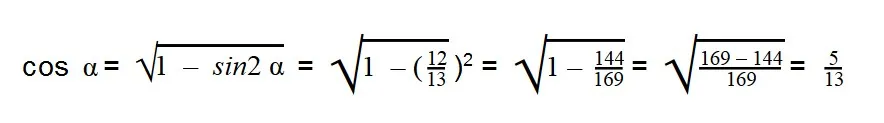
- Нам известны значения sin α и cos α, поэтому можно легко найти тангенс, используя формулу:
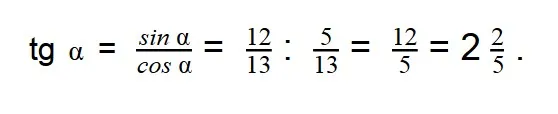
- Таким же образом, используя формулу, вычисляем значение котангенса:
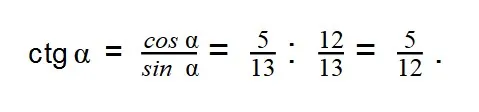
Ответ:
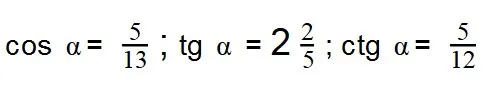
Задачка 2. Найдите значение cos α,
если:
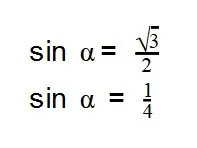
Как решаем:
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
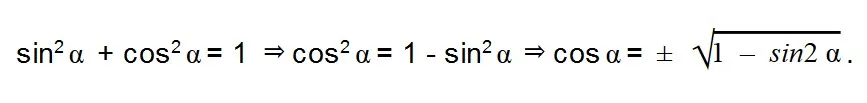
- Выражаем cos α из тригонометрической единицы:
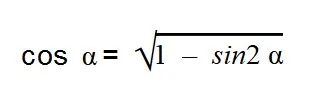
- Далее подставляем значения sin α:
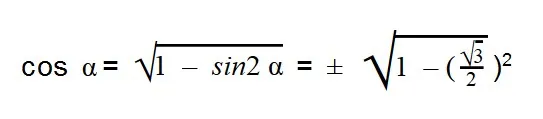
- Вычисляем:
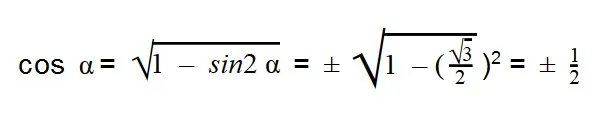
- То же самое проделываем со вторым значение sin α
Подставляем значения sin α:
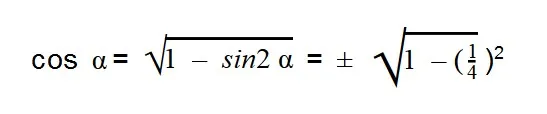
- Вычисляем:
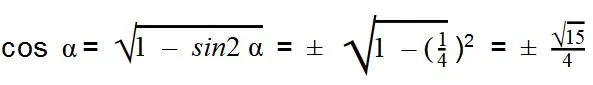
Ответ:
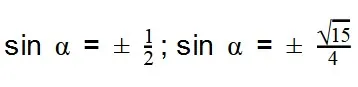
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.