Как решать тригонометрические уравнения

Простейшие тригонометрические уравнения

Начнём с базовых тригонометрических уравнений, к которым будем сводить более сложные.

Уравнение вида

Уравнение имеет решения, если .

Общий вид решения: , где — любое целое число.

Уравнение вида

Уравнение также имеет решения при условии, что .

Общий вид решения: , где .

Уравнение вида

Уравнение имеет решение для любого значения .

Общий вид решения: , где .

Уравнение вида

Уравнение также решается для любого значения .

Общий вид решения: , где .

Общие виды решения, а также решения для частных случаев можно рассмотреть в таблице:

A	a	−1	0	1

Тригонометрическая окружность и графики функций

Тригонометрическая окружность и графики функций позволяют наглядно увидеть решения простейших уравнений и правильно определить периодичность.

Тригонометрическая окружность — это окружность с радиусом 1, центр которой находится в начале координат: на ней ось x соответствует косинусу, а ось y — синусу угла.

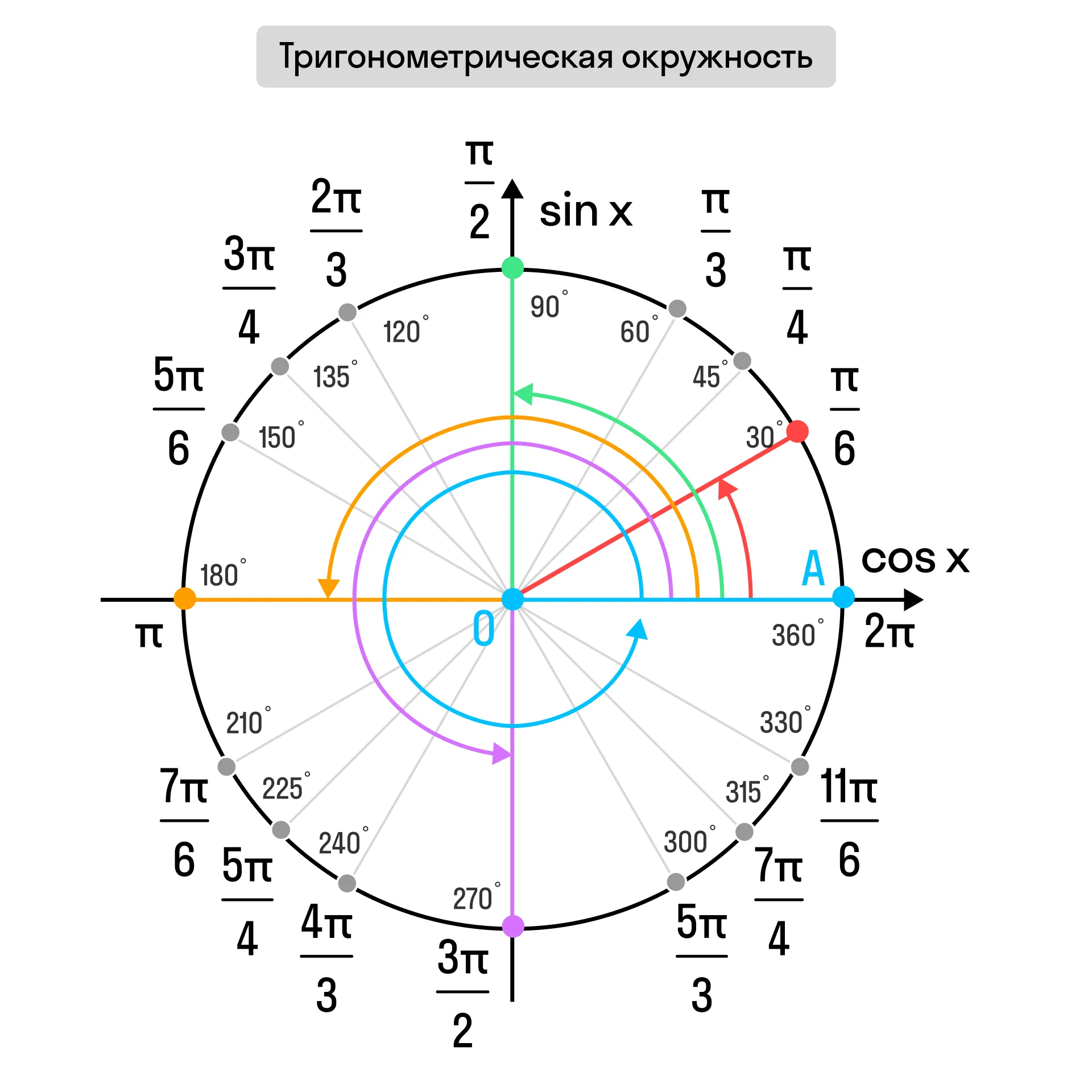
Как ей пользоваться? Рассмотрим на примере уравнения :

1. На тригонометрической окружности на оси синусов отмечаем значение , от этой точки проводим пунктирные линии до пересечения с окружностью.

   

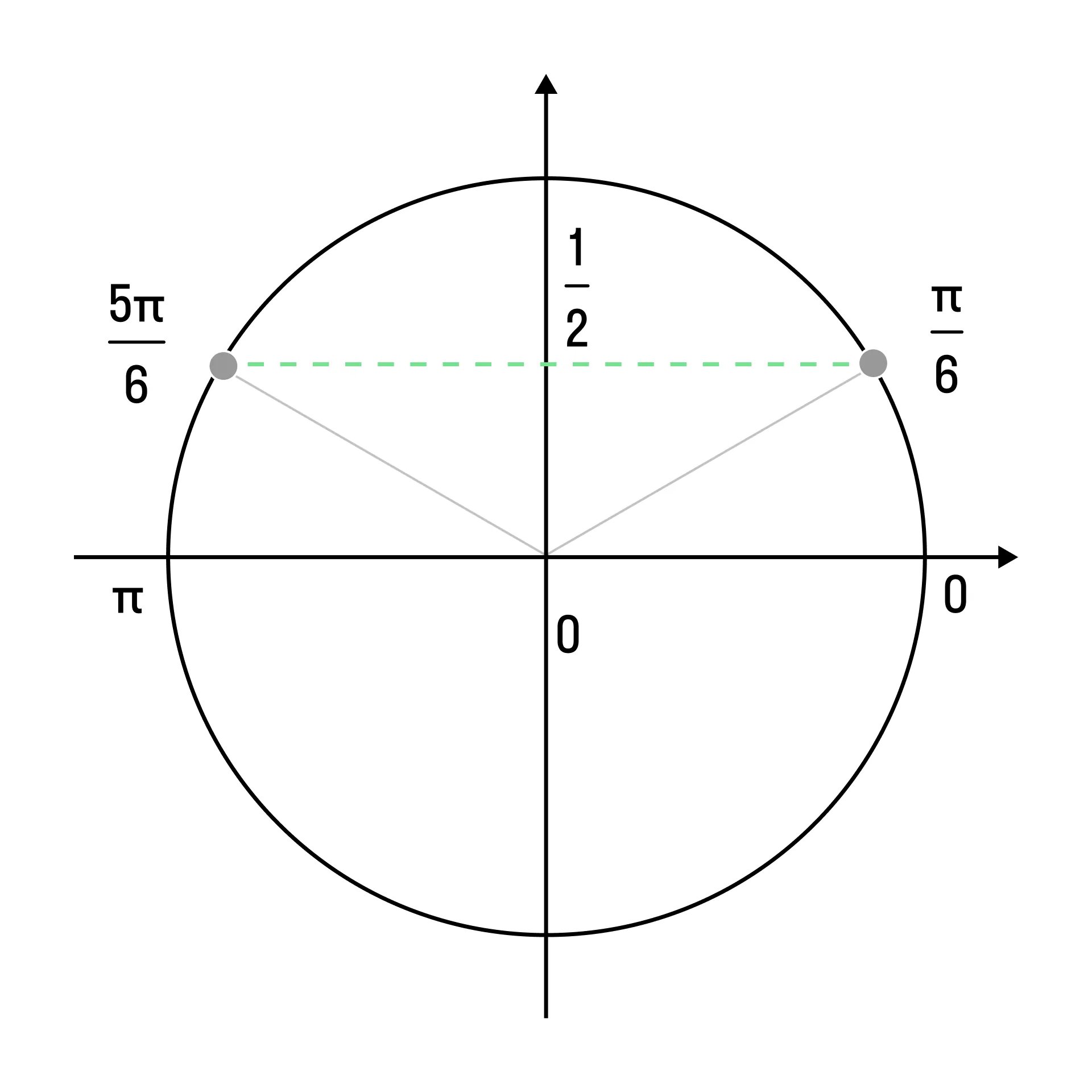
2. Это значения синуса соответствует углам, равным и соответственно.

   Общее решение: , где .

   Частные решения:

   , где

   , где

Те же рассуждения можно проверить по графику синуса — синусоиде.

150.4K

Какая профессия тебе подходит? Узнай за 10 минут!

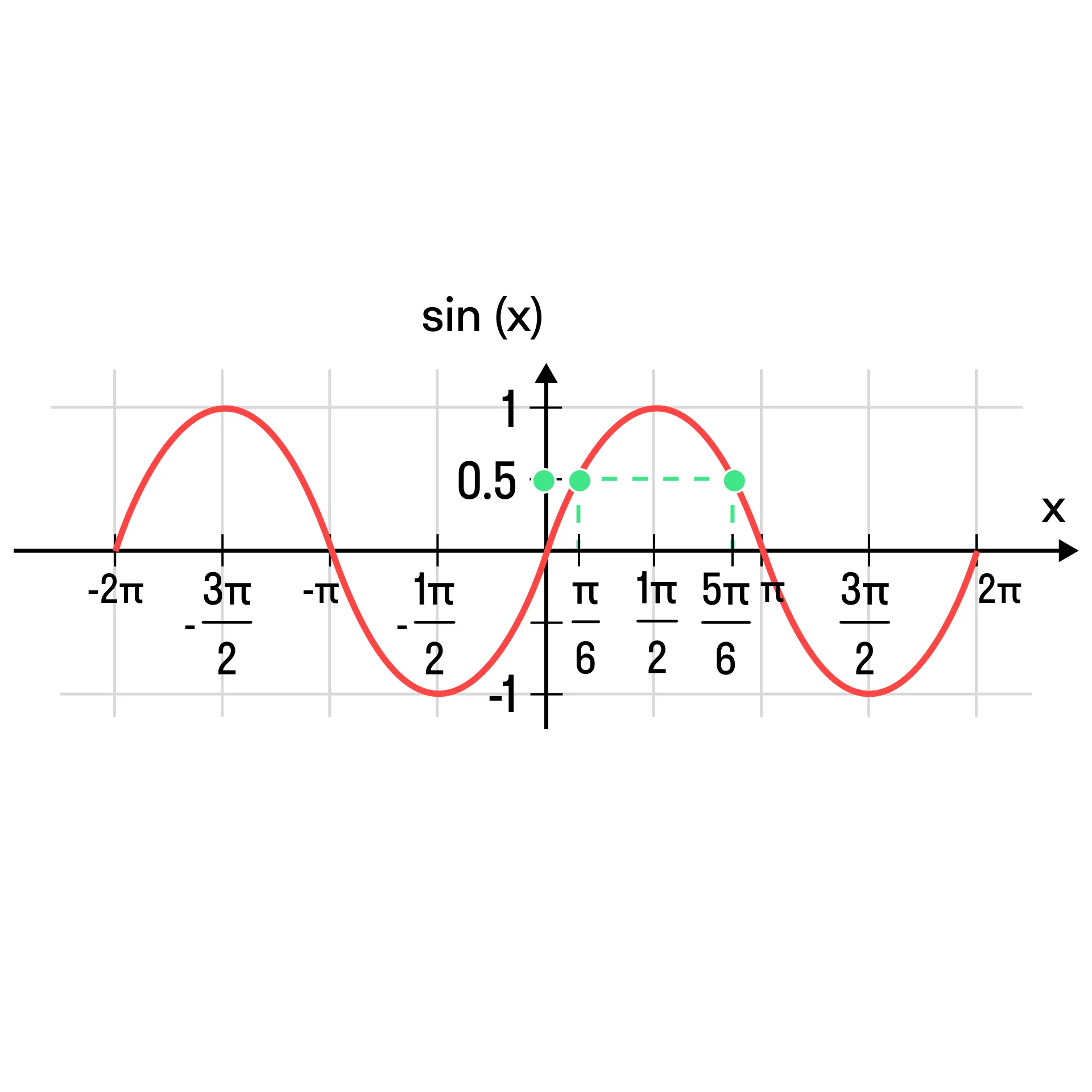
Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Усложнённые виды уравнений

Конечно, помимо простейших уравнений есть и более сложные виды. Важно уметь определять алгоритм действия соответствующий типу уравнения и при каждом удобном случае преобразовывать выражения, упрощать их.

Общий вид алгоритма решения тригонометрических уравнений выглядит так:

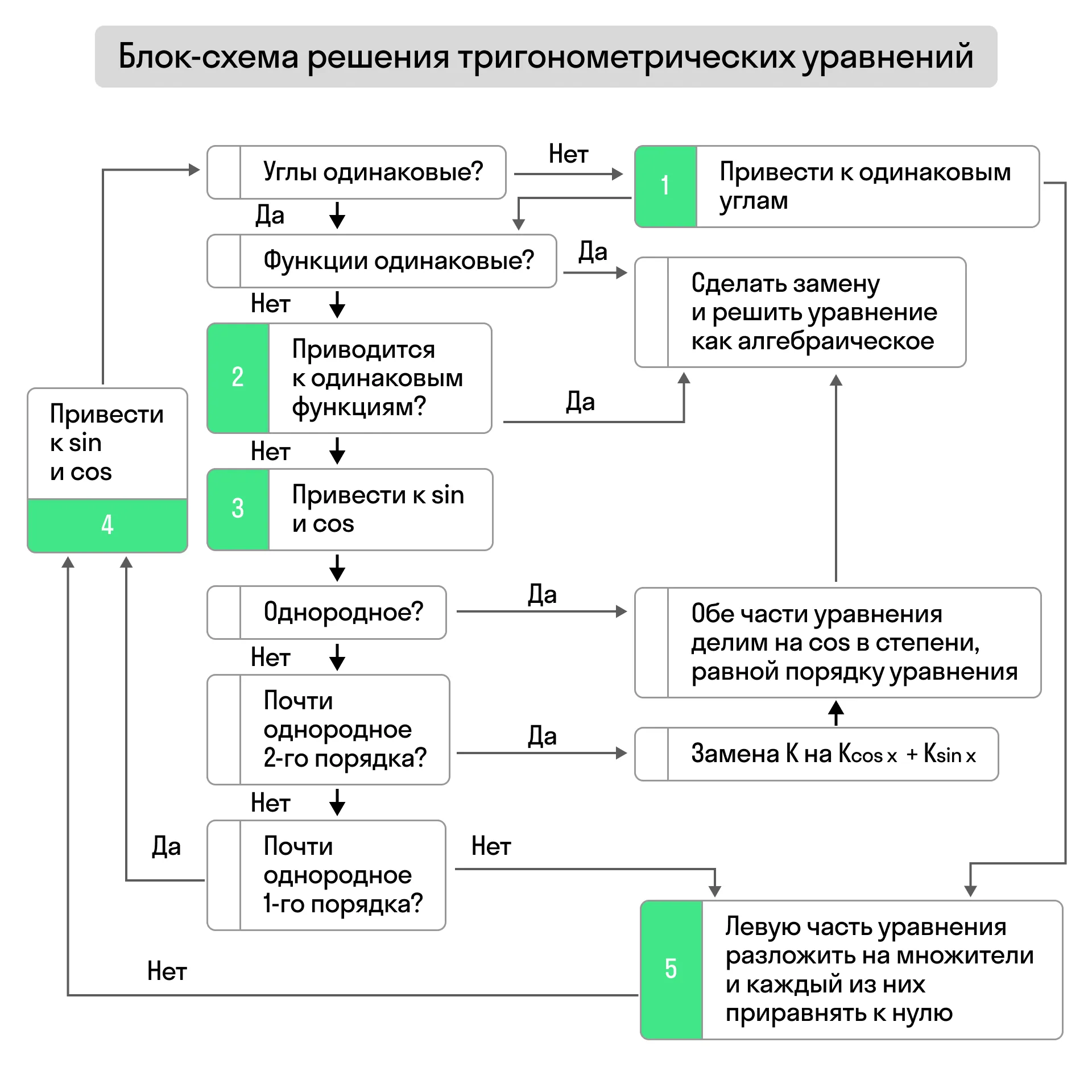
А теперь остановимся подробнее на каждом виде уравнений.

Уравнения вида и подобные ему

Уравнения вида сводятся к простейшим с помощью замены переменной.

Пример:

Пусть , тогда

, где

, где

тогда

, где

, где

Всё разделим на число 3:

, где

Уравнения, сводимые к квадратным

Некоторые тригонометрические уравнения можно свести к квадратным с использованием замены переменной.

881.4K

Как решать квадратные уравнения? Формулы, примеры и онлайн-калькуляторЧитать →

Шаги:

1. Используем замену переменной.

2. Найдем значения переменной и откинем корни, не соответствующие ОДЗ.

3. Найдем значение х, сведя уравнение к простому.
   

Пример:

Пусть , тогда

тогда

, где

, где

Ответ: , где и , где .

Однородные тригонометрические уравнения

Однородные тригонометрические уравнения — это уравнения, в которых все члены содержат тригонометрические функции одного и того же угла, и их можно свести к простейшим уравнениям путем деления всех членов на одну из тригонометрических функций.

Например:

— однородное уравнение.

1. Обе функции взяты от угла x.

2. Левую и правую части можно разделить на для упрощения уравнения:

   и т.д.

— общий вид однородного уравнения первой степени.

— общий вид однородного уравнения второй степени.

Решение однородных тригонометрических уравнений сводится к следующим основным шагам:

1. Вынесение общего множителя за скобки (такое упрощение позволяет разделить уравнение на несколько простейших).

2. Решение каждого множителя отдельно.

3. Все найденные решения составляют общий ответ.

Пример:

Вынесем общий множитель за скобку:

Приравняем оба множителя к нулю:

Уравнение — однородное, разделим обе части на , где

Ответ: и , где

Уравнения с разными тригонометрическими функциями одного угла

Порой деление на одну тригонометрическую функцию (как в однородных уравнениях) не приносит существенных результатов. В таком случае можно воспользоваться основными тригонометрическими тождествами и выразить все функции в уравнении через одну. Например, все функции выразить через синус или тангенс.

Для этого нам понадобятся следующие тождества:

Пример:

ОДЗ:

Воспользуемся определениями тангенса и котангенса:

Приведём все к одному знаменателю, преобразуем и получим

Воспользуемся тождеством и заменим :

Введём замену переменной и решим квадратное уравнение:

Тогда

корень не подходит под ОДЗ

Ответ: .

Уравнения с тригонометрическими функциями разных углов

Для решения таких уравнения часто применяют использование тригонометрических тождеств, преобразование уравнений с помощью формул приведения и формул двойного и тройного угла, а также замена переменных.

Главная задача — свести разные углы к одному, а дальше определить вид и решать по алгоритмам, которые мы разобрали выше.

Пример:

Воспользуемся формулой двойного угла:

Вынесем общий множитель

Ответ: и .

Уравнения с использованием формул суммы или разности

В подобных случаях могут использоваться как формулы суммы и разности самих функций, так и их аргументов:

В данном случае мы можем:

• использовать формулы напрямую, т. е. преобразовать уравнение с их помощью;

• преобразовать уравнение таким образом, чтобы получилась формула суммы или разности.

Пример:

Разделим все части уравнения на :

Заметим, что полученное выражение похоже на формулу , если заменить значение на или

Другие типы уравнений

Помимо вышеперечисленных видов, на уроках математики вы встретитесь:

• с тригонометрическими уравнениями с параметром;

• комбинированными уравнениями (где используется сразу несколько методов преобразований);

• смешанными уравнениями, которые содержат как тригонометрические, так и другие виды функций, например, экспоненциальные или логарифмические.

Если вы столкнулись с чем-то необычным, не паникуйте сразу, а воспользуйтесь нашими советами:

1. Используйте тригонометрические тождества. Применение тригонометрических тождеств позволяет упростить уравнения и свести их к более простым формам.

2. Приведите уравнение к стандартной форме. Преобразуйте уравнение так, чтобы оно включало только одну тригонометрическую функцию или простые комбинации функций. Это можно сделать, используя тождества или замену переменной.

3. Используйте графический метод. Для некоторых уравнений может быть полезно построить графики тригонометрических функций и найти их точки пересечения. Это дает визуальное представление о решениях и может помочь в нахождении всех корней уравнения.

4. Работайте с периодичностью функций. Учитывайте периодичность тригонометрических функций при поиске всех решений. Если уравнение имеет решение в интервале [0, 2π), то общее решение можно найти, добавив 2πk, где k ∈ Z.

Чтобы сделать подготовку к экзаменам более эффективной и увлекательной, мы предлагаем вам воспользоваться нашим бесплатным тренажёром. Он поможет вам отточить навыки, освоить новые методы решения задач и подготовиться к экзаменам с комфортом. Переходите по ссылке и начните практиковаться уже сегодня!