Неполные квадратные уравнения

Для кого эта статья:

• студенты и ученики старших классов, изучающие математику
• абитуриенты, готовящиеся к экзаменам по математике
• родители, активно вовлеченные в обучение своих детей

Калькулятор неполных квадратных уравнений

Основные понятия

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.

Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:

• если D < 0, корней нет;
• если D = 0, есть один корень;
• если D > 0, есть два различных корня.

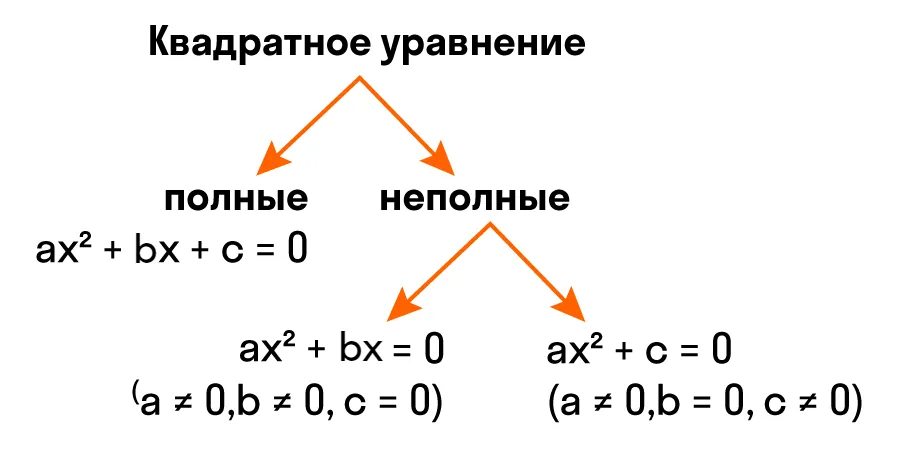
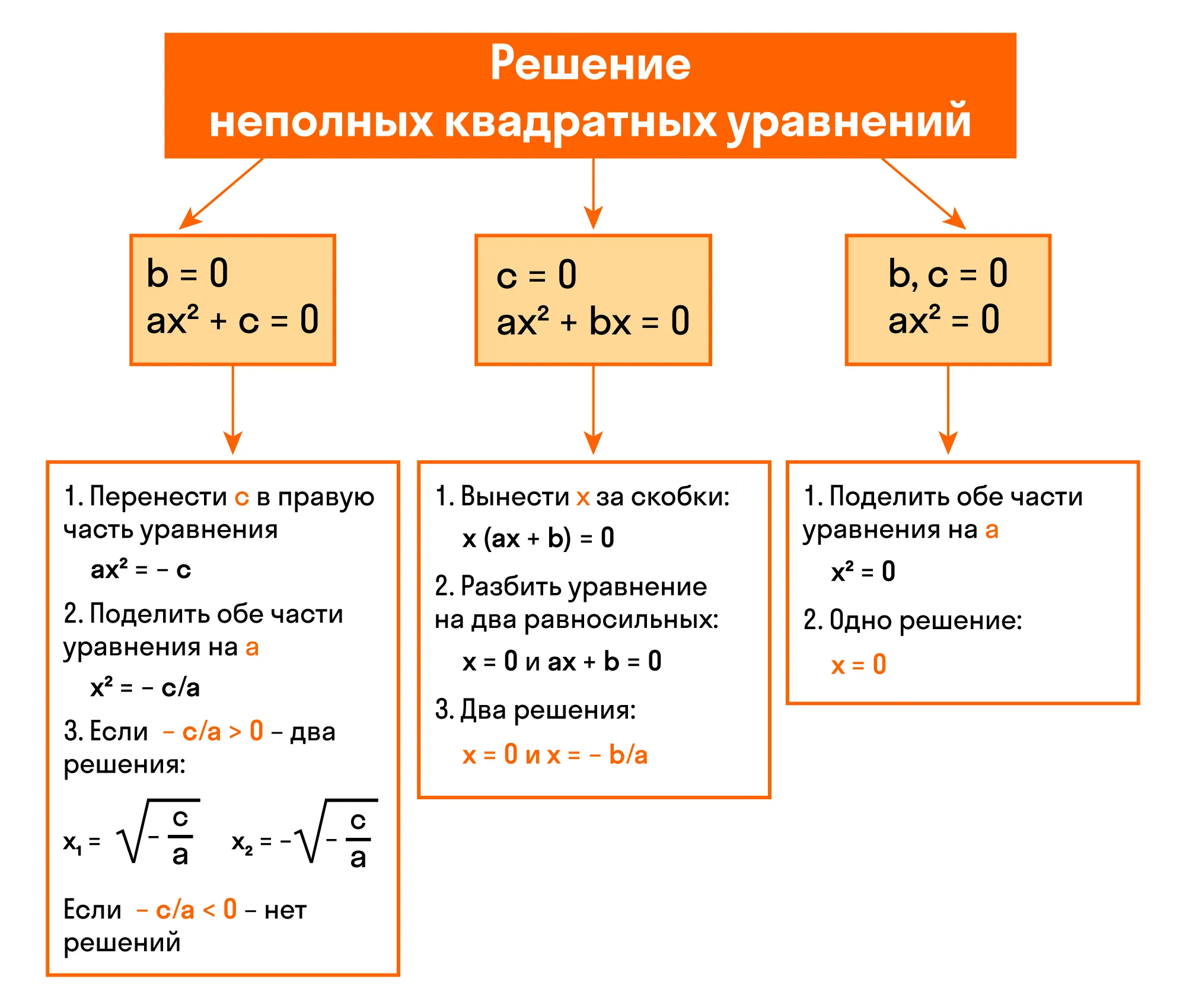
Неполное квадратное уравнение — это уравнение вида ax² + bx + c = 0, где хотя бы один из коэффициентов b или c равен нулю.

Неполные квадратные уравнения бывают трех видов:

• Если b = 0, то квадратное уравнение принимает вид ax² + 0x+c=0 и оно равносильно ax² + c = 0.
• Если c = 0, то квадратное уравнение выглядит так ax² + bx + 0 = 0, иначе его можно написать как ax² + bx = 0.
• Если b = 0 и c = 0, то квадратное уравнение выглядит так ax² = 0.

Такие уравнения отличаются от полного квадратного тем, что их левые части не содержат слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

214.5K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Прокачивай знания на курсах математики

• Выбирай из 1200+ репетиторов по математике

• Записывайся на бесплатные курсы для детей

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

• ax² = 0, ему отвечают коэффициенты b = 0 и c = 0;
• ax² + c = 0, при b = 0;
• ax² + bx = 0, при c = 0.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по профильной математике.

Как решить уравнение ax² = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0.

Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0.

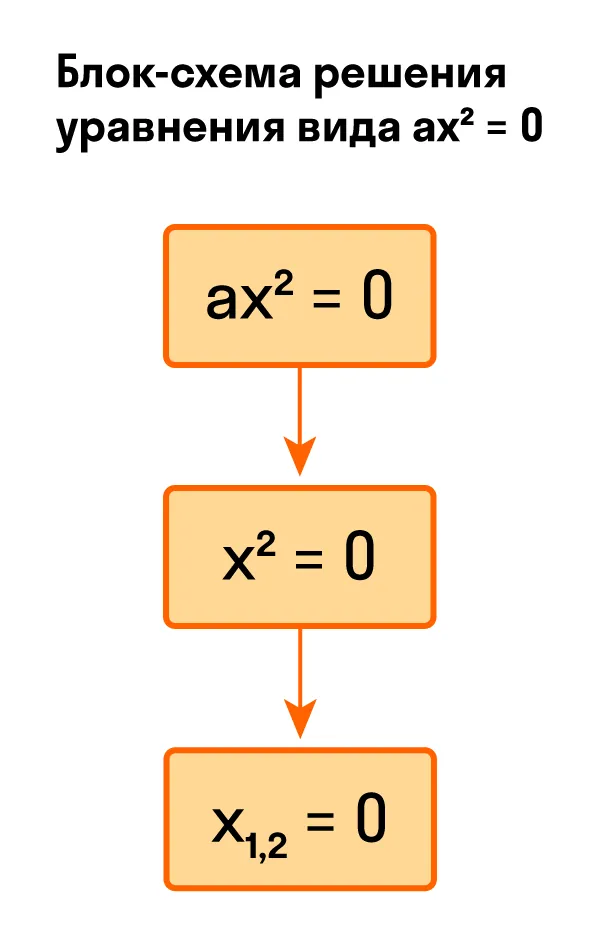
Пример 1. Решить −5x² = 0.

Как решаем:

 

1. Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
2. По шагам решение выглядит так:

   −5x² = 0

   x² = 0

   x = √0

   x = 0

   Ответ: 0.

Как решить уравнение ax² + с = 0

Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. То есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:

• перенесем c в правую часть: ax² = - c,
• разделим обе части на a: x² = - c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение - c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если - c/а < 0, то уравнение x² = - c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при - c/а < 0 ни для какого числа p равенство р² = - c/а не является верным.

Если - c/а > 0, то корни уравнения x² = - c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = - c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = - c/а. Ура, больше у этого уравнения нет корней.

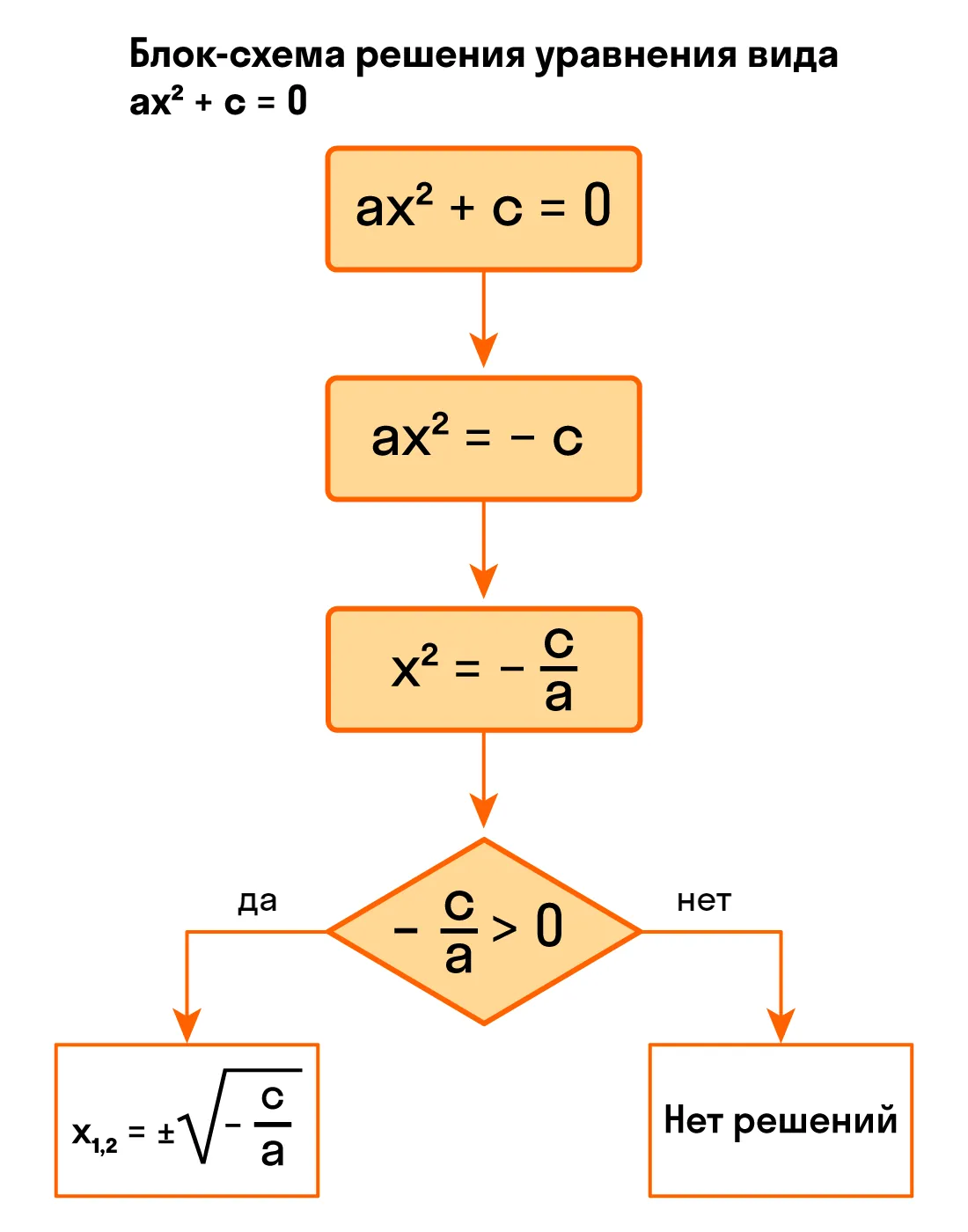
В двух словах квадратное уравнение ax² + c = 0 равносильно уравнению ax² + c = 0, которое:

• не имеет корней при - c/а < 0;
• имеет два корня х = √- c/а и х = -√- c/а при - c/а > 0.

Пример 1. Найти решение уравнения 9x² + 4 = 0.

Как решать:

 

1. Перенесем свободный член в правую часть:

   9x² = - 4

2. Разделим обе части на 9:

   x² = - 4/9

3. В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 9x² + 4 = 0 не имеет корней.

Пример 2. Решить -x² + 9 = 0.

Как решаем:

 

1. Перенесем свободный член в правую часть:

   -x² = -9

2. Разделим обе части на -1:

   x² = 9

3. Найти корни:

   x = √9

   x = -3, 3

Ответ: уравнение -x² + 9 = 0 имеет два корня -3; 3.

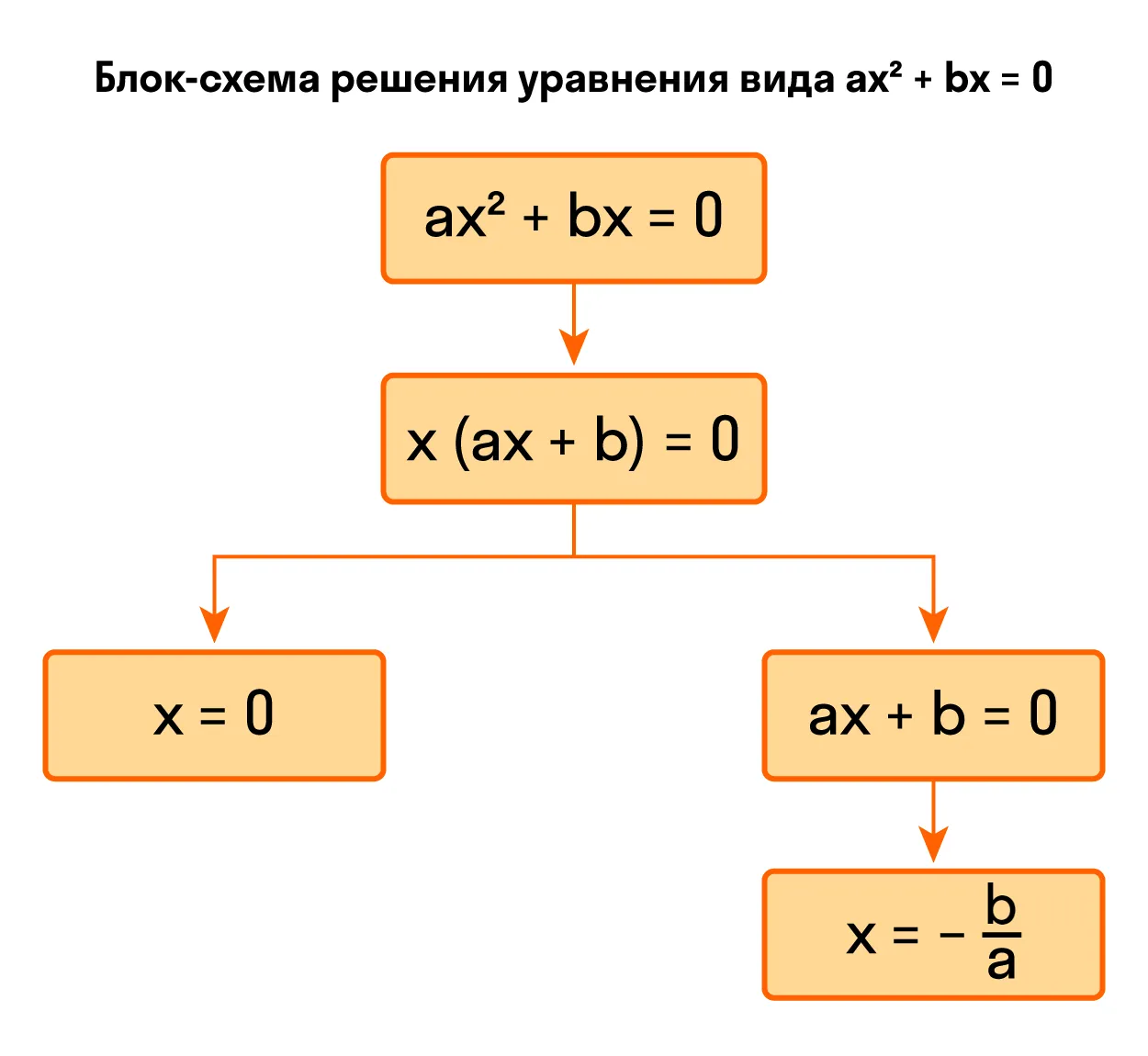
Как решить уравнение ax² + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Квадратное уравнение без с непривычно решать только первые несколько примеров. Запомнив алгоритм, будет значительно проще щелкать задачки из учебника.

Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня:

• x = 0;
• x = −b/a.

Пример 1. Решить уравнение 2x² - 32x = 0

Как решать:

 

1. Вынести х за скобки

   х(2x - 32) = 0

2. Это уравнение равносильно х = 0 и 2x - 32 = 0.
3. Решить линейное уравнение:

   2x = 32,

   х = 32/2

4. Разделить:

   х = 16

5. Значит корни исходного уравнения — 0 и 16.

Ответ: х = 0 и х = 16.

Пример 2. Решить уравнение 3x² - 12x = 0

Как решать:

Разложить левую часть уравнения на множители и найти корни:

Ответ: х = 0 и х = 4.

Для удобства мы собрали все виды неполных квадратных уравнений и способы их решения на одной картинке-шпаргалке.

Тест по теме «Неполные квадратные уравнения»