Вектор

Определение и обозначение вектора

Вектор в геометрии — это отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом. В некоторых учебниках вектор могут называть направленным отрезком.

Вектор обозначается одной строчной буквой латинского алфавита или двумя заглавными со стрелкой (в некоторых случаях — прямой линией) сверху.

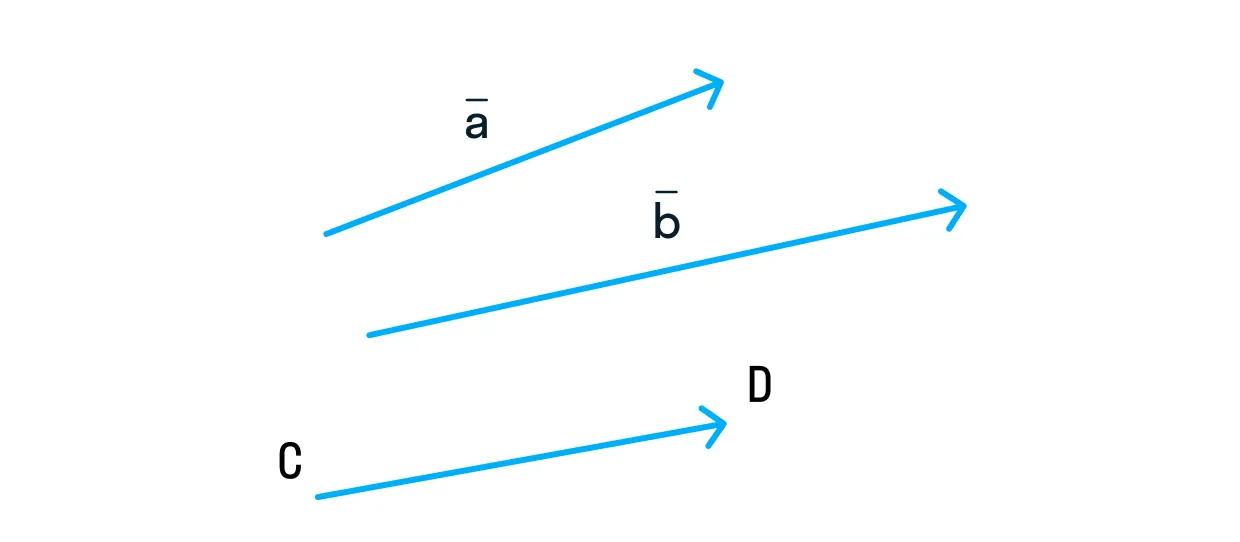
Интересно, что порядок букв в названии вектора имеет значение! Первая буква отвечает за начало вектора, а последняя — за его конец. Поэтому и — абсолютно разные векторы.

Виды векторов

Во-первых, векторы бывают коллинеарными и неколлинеарными.

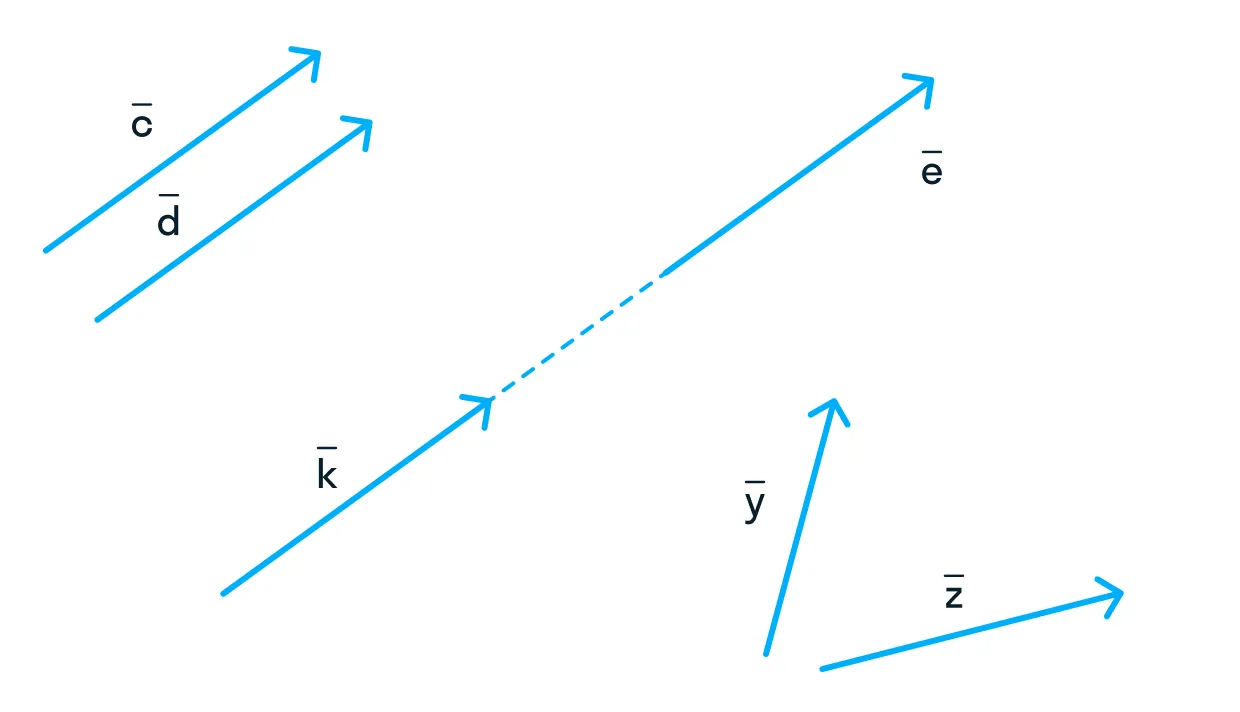
Коллинеарными называют те векторы, которые лежат на одной прямой или параллельных прямых. На рисунке и и являются коллинеарными, а и относительно друг друга — нет.

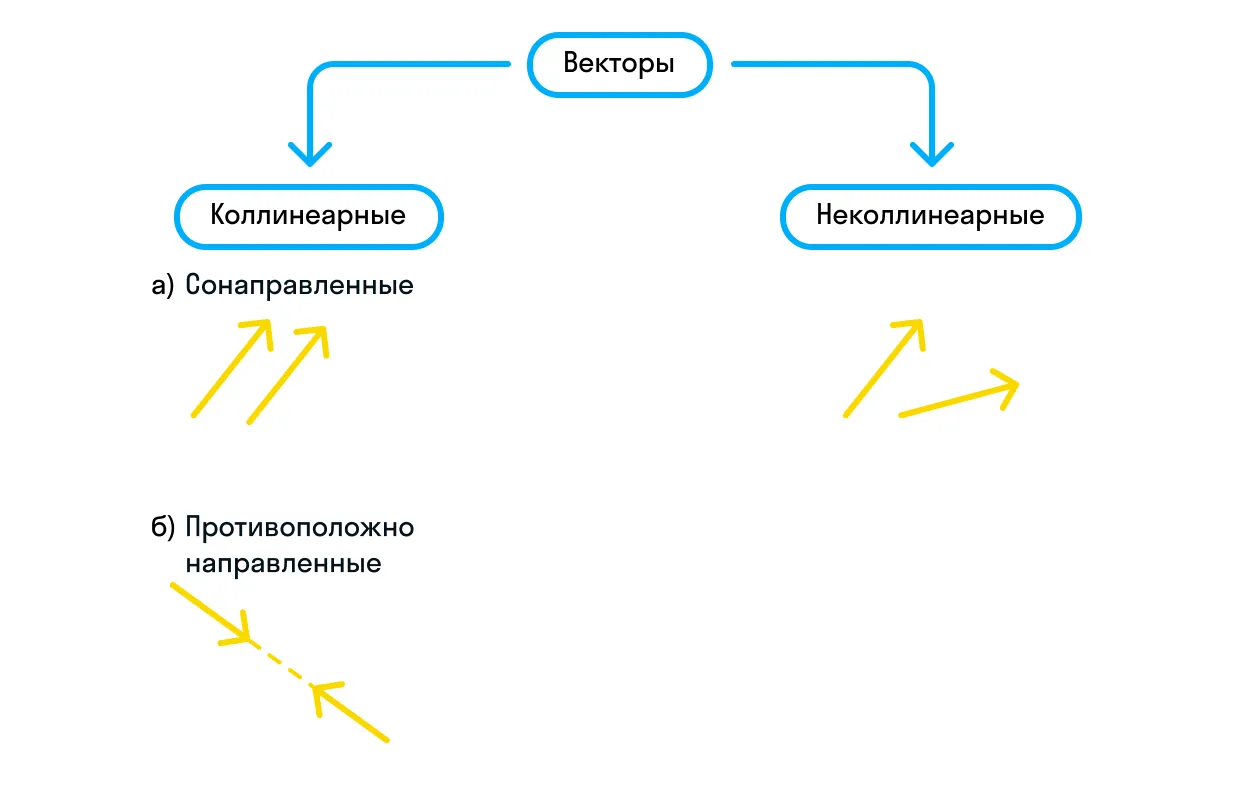
Векторы различаются и по направлению. Если векторы уже являются коллинеарными, они могут быть сонаправленными или противоположно направленными. Сонаправленные векторы обозначаются так: Если же они противоположно направлены, мы можем записать это следующим образом:

Равными являются те векторы, которые одновременно и коллинеарны, и сонаправлены, а также имеют одинаковую длину.

Нулевой вектор — вектор, длина которого равна нулю. Чаще всего его обозначают так: Он считается коллинеарным любому вектору.

Иногда в геометрии вводят дополнительные понятия, рассмотрим и их:

• Закреплённый вектор — отрезок с упорядоченными концами: если С — точка начала вектора, а Е — точка конца, тогда (это то, что мы понимаем под обычным вектором в школьной геометрии).

• Свободный вектор — вектор, начало и конец которого не закреплены. Его можно перемещать как вдоль прямой, на которой он находится, так и параллельно этой прямой. По сути под свободным вектором понимают множество закреплённых векторов.

178.1K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Сложение и вычитание векторов

Действия с векторами описываются и в алгебре, и в геометрии. Сегодня мы рассмотрим способы, благодаря которым можно сложить и вычесть векторы, не зная их координат.

Сложение: метод треугольника

Представим, что в пространстве заданы векторы и которые нам необходимо сложить. Эта задача особенно актуальна для физиков, поскольку такие векторные величины, как сила, часто приложены к одному и тому же телу. В таком случае возникает вопрос: а как же рассчитать результирующее действие всех этих сил?

В этом на помощь физикам приходит математика — царица наук! Чтобы сложить два вектора, необходимо:

1. Отложить начало одного вектора от конца другого.

2. Вектор их суммы будет совпадать с вектором , который соединяет начало вектора с концом вектора

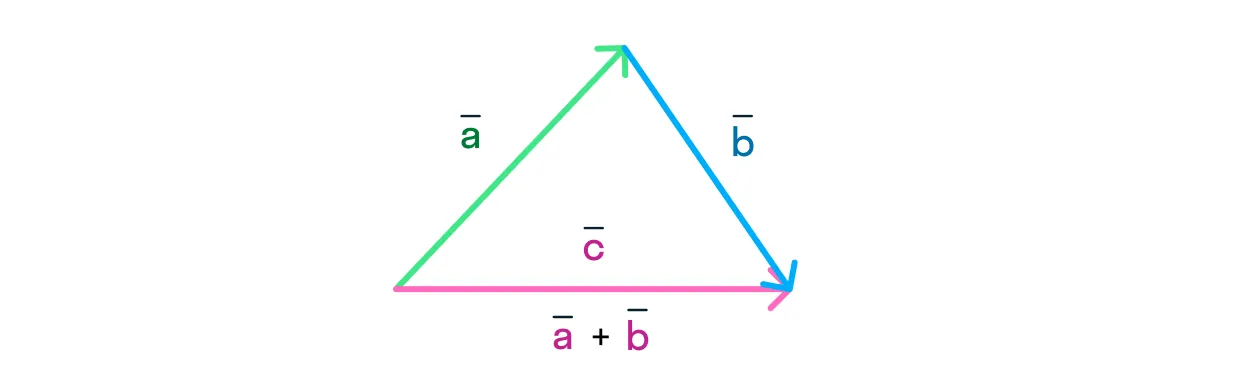
Сложение: метод параллелограмма

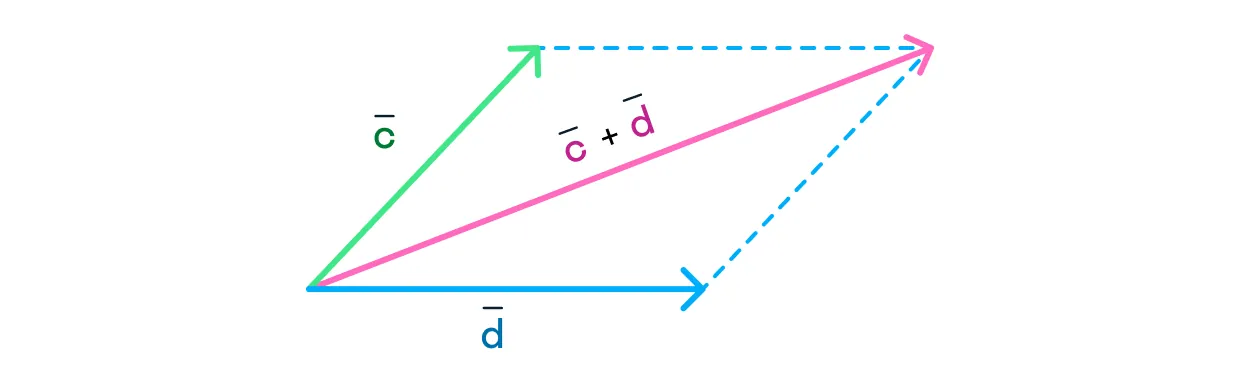
Сложить векторы можно и по-другому, используя метод параллелограмма:

1. Совместим между собой начала и

2. Отложим от конца вектор, равный

3. Отложим от конца вектор, равный

4. Благодаря пунктам 2 и 3 мы получили параллелограмм (четырёхугольник, противоположные стороны которого параллельны и равны).

5. Проведём диагональ параллелограмма между и на которой будет лежать вектор, равный сумме и

Задача решена, вы великолепны!

Сложение: метод многоугольника

А что если векторов больше, чем два? На эту проблему математика уже подготовила решение: воспользуемся расширенным методом треугольника, который получил название «метод многоугольника».

Согласно этому методу мы последовательно совмещаем конец и начало векторов, а после изображаем суммирующий вектор, начало которого совпадает с началом первого вектора, а конец — с концом последнего. Лучше всего рассмотреть это на чертеже:

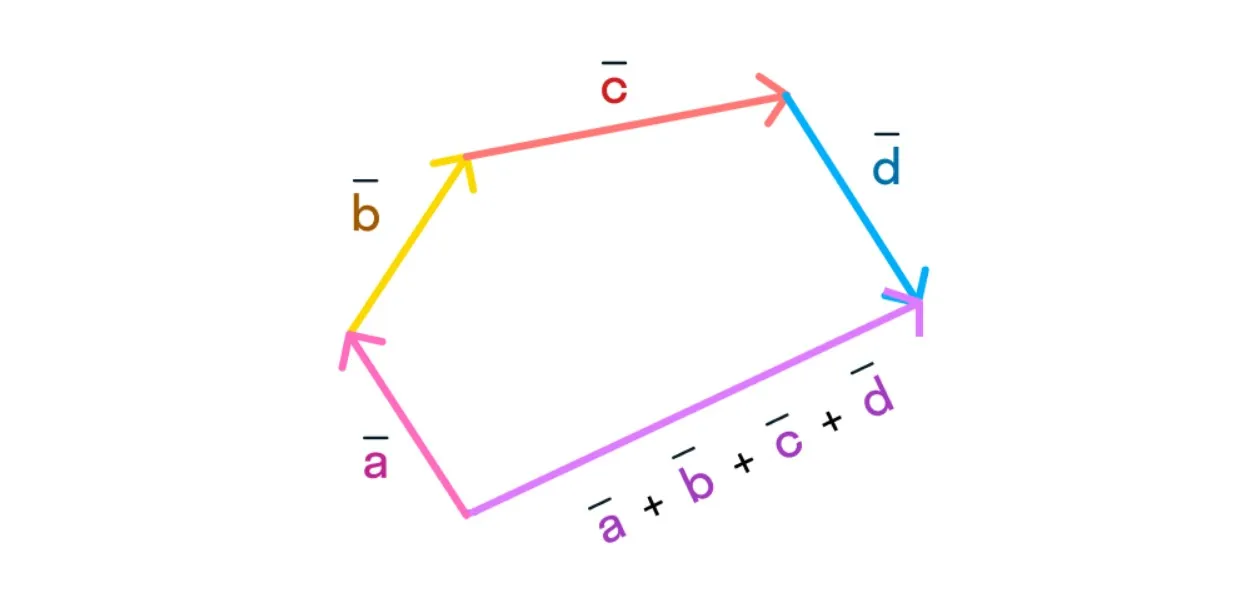
Вычитание векторов

Продолжаем проделывать с векторами всевозможные действия, на этот раз вычитание. Математики знают, что вычитание — это по своей сути то же сложение, но с обратным числом.

С векторами работает та же штука: вместо вычитания попробуем прибавить вектор, противоположно направленный исходному:

Изобразим разность векторов с помощью уже знакомого нам правила треугольника:

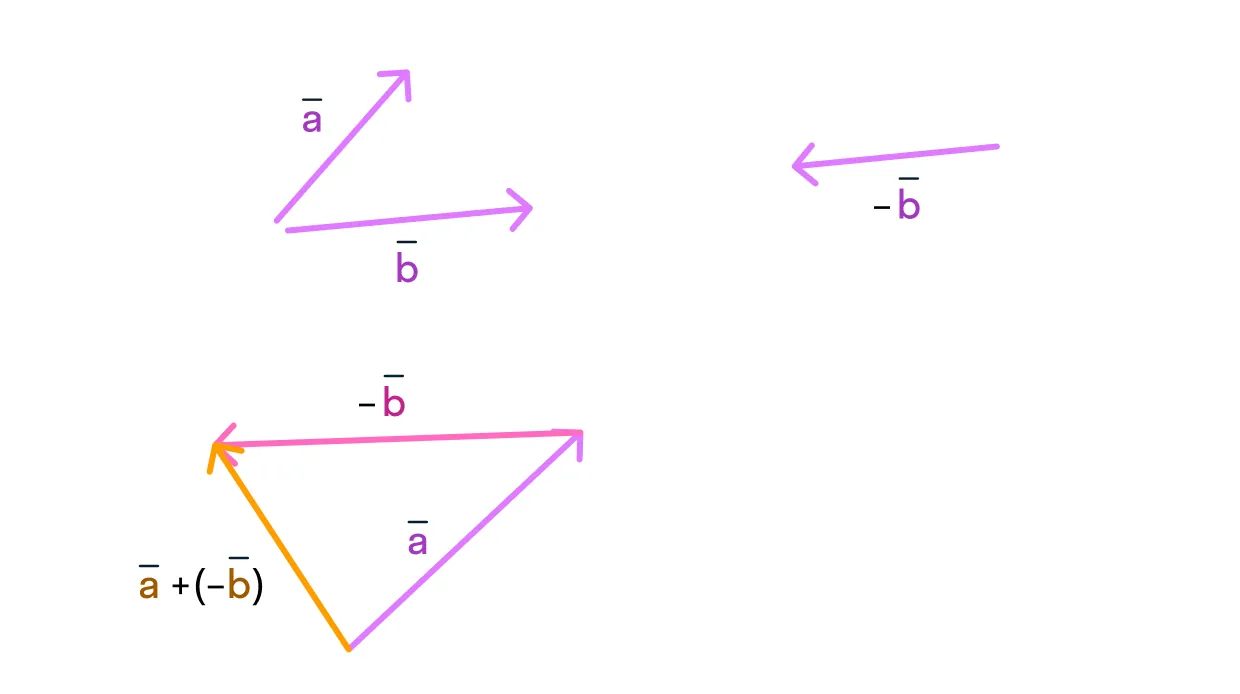
Боитесь запутаться в векторах сонаправленных и противоположно направленных? Существует отдельное правило для их вычитания:

1. Отложим один вектор от начала другого.

2. Тогда вектор их разности совпадает с вектором, начало которого совмещено с концом вычитаемого вектора, а конец — с концом уменьшаемого.

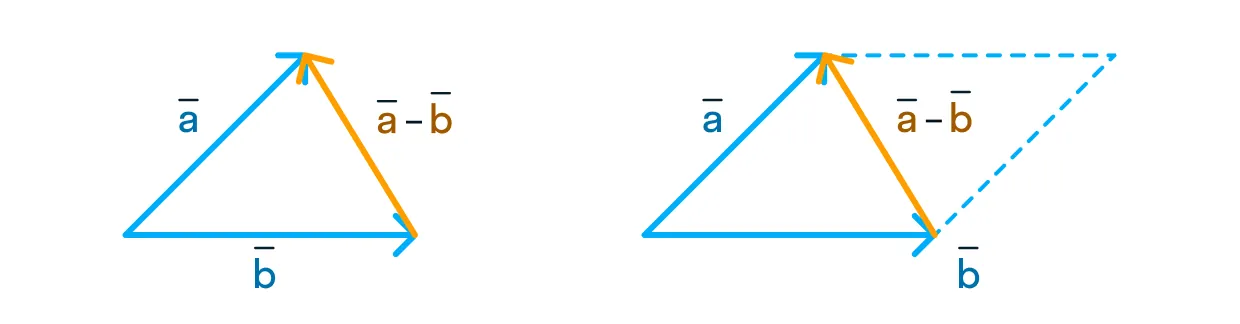
Этот метод схож и с методом параллелограмма, но в этом случае мы берём другую диагональ.

👉 Сложно? Открой для себя новые возможности в онлайн школе Skysmart!
Любые правила и формулы простым языком!

Координаты вектора на плоскости и в пространстве

Для выполнения остальных действий с векторами нам необходимо поместить их в такую систему координат, чтобы можно было определить их положение относительно друг друга. Для этого используют декартову систему координат, которой можно пользоваться как на плоскости с осями X и Y, так и в пространстве с осями X, Y, Z.

Тогда, если находится на плоскости, его координаты можно выразить как если в пространстве —

Базисные векторы — это векторы, каждый из которых направлен вдоль своей оси координат, в трёхмерном пространстве их обозначают

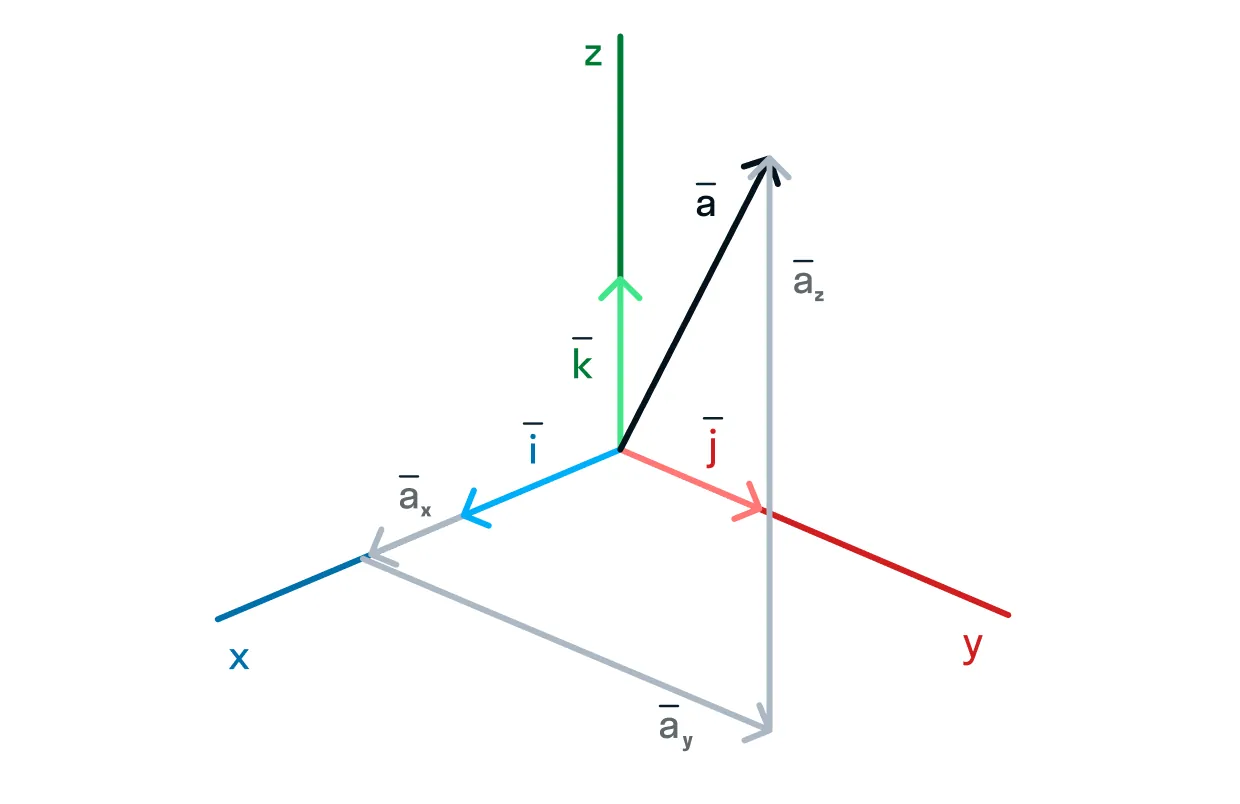
Любой вектор в трёхмерном пространстве можно разложить по трём базисным векторам.

с координатами можно записать так:

Умножение вектора на число

Представьте, что нам необходимо растянуть вектор в два раза или же сжать, но уже в три. За все эти действия отвечает одна простая задача: умножение вектора на число.

Для того чтобы увеличить или уменьшить вектор в некоторое количество раз, необходимо умножить все координаты вектора на это число.

Таким образом, если задан координатами то — Кстати, подобным образом можно перевернуть вектор, направив его в противоположную сторону:

Длина вектора

Длина вектора — одно из основных понятий в этом разделе. И неудивительно, ведь она характеризует его протяженность в пространстве и выражается числом.

Итак, длина вектора — это расстояние между его началом и концом. Её часто называют модулем, что отражается и в обозначении. Если нам необходимо найти длину мы так и запишем:

Длину вектора можно найти разными способами, вот основные:

1. через координаты вектора;

2. через координаты точек начала и конца вектора;

3. через теорему косинусов.

Давайте вместе разберём все методы!

Длина вектора через его координаты

Если задан через координаты то его длину можно найти как

Почему мы можем быть уверены, что эта формула правильная? Рассмотрим вектор в декартовой системе координат.

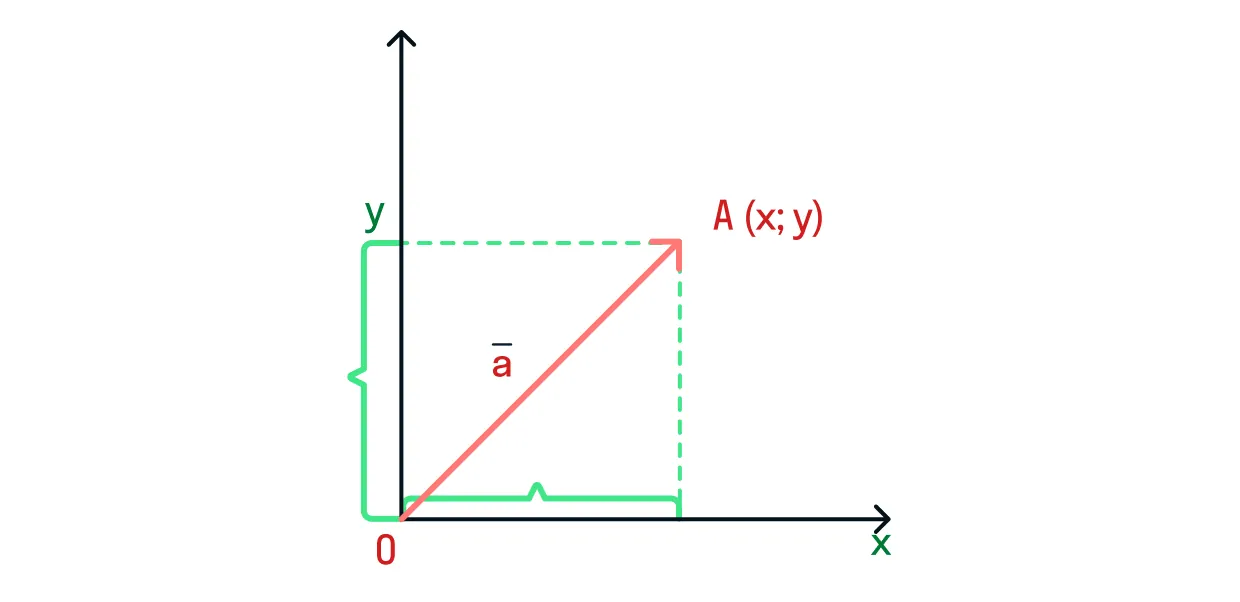
Отложим вектор от точки с координатами Тогда этот вектор можно назвать , и так как мы строили его из начала координат, координаты вектора могут быть найдены как

Рассчитаем длину через теорему Пифагора:

Задача 1

Посчитайте, чему равен модуль , если его координаты

Решение:

Модуль вектора — это его длина, а значит,

Задача 2

Длина Чему равна координата по оси , если координата по оси

Решение:

Длина вектора через координаты точек начала и конца

Для начала давайте вспомним, как задать координаты вектора через координаты его начала и конца.

Рассмотрим где и Тогда координаты вектора можно выразить так:

Мы уже знаем, как найти длину вектора через его координаты, поэтому подставим полученное выражение в формулу:

Задача 3

Найдите длину если и

Решение:

Задача 4

Рассчитайте координату по точки вектора , если его длина равна а

Решение:

Остановимся здесь и подставим известные числа в формулу:

или

Длина вектора через теорему косинуса

К сожалению, в задачах не всегда даны координаты точек вектора или его самого. В таком случае мы воспользуемся теоремой косинуса. Давайте вспомним её формулировку.

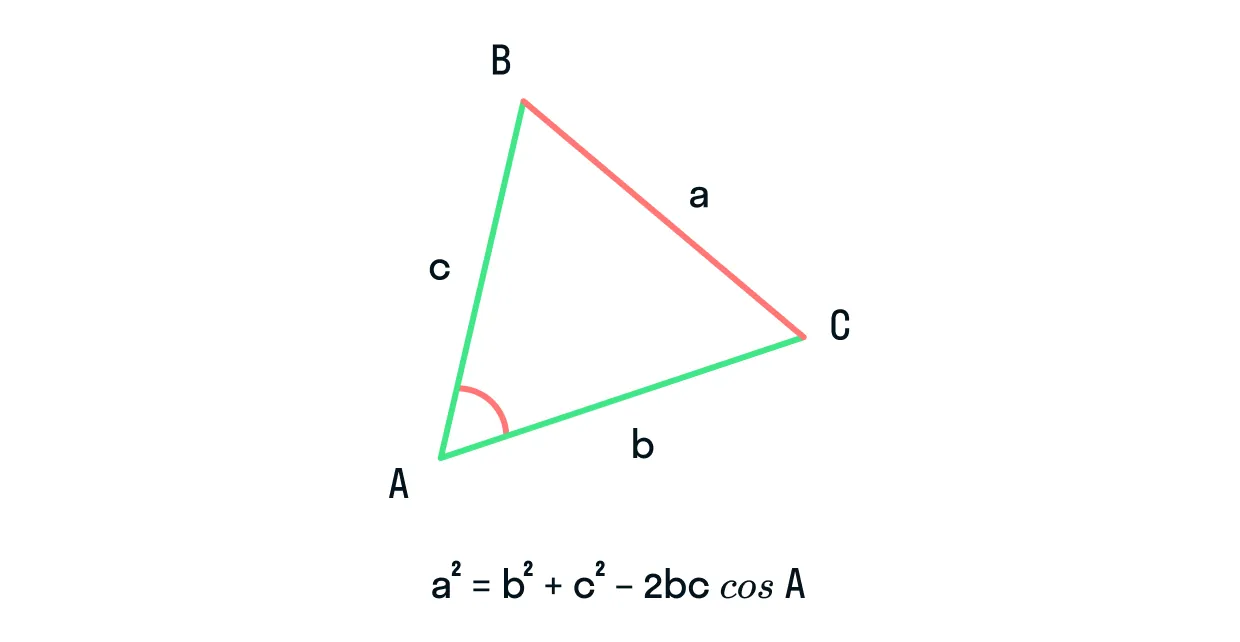
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Формула теоремы косинусов:

Эту теорему можно применить и в векторной форме. Немного изменим рисунок:

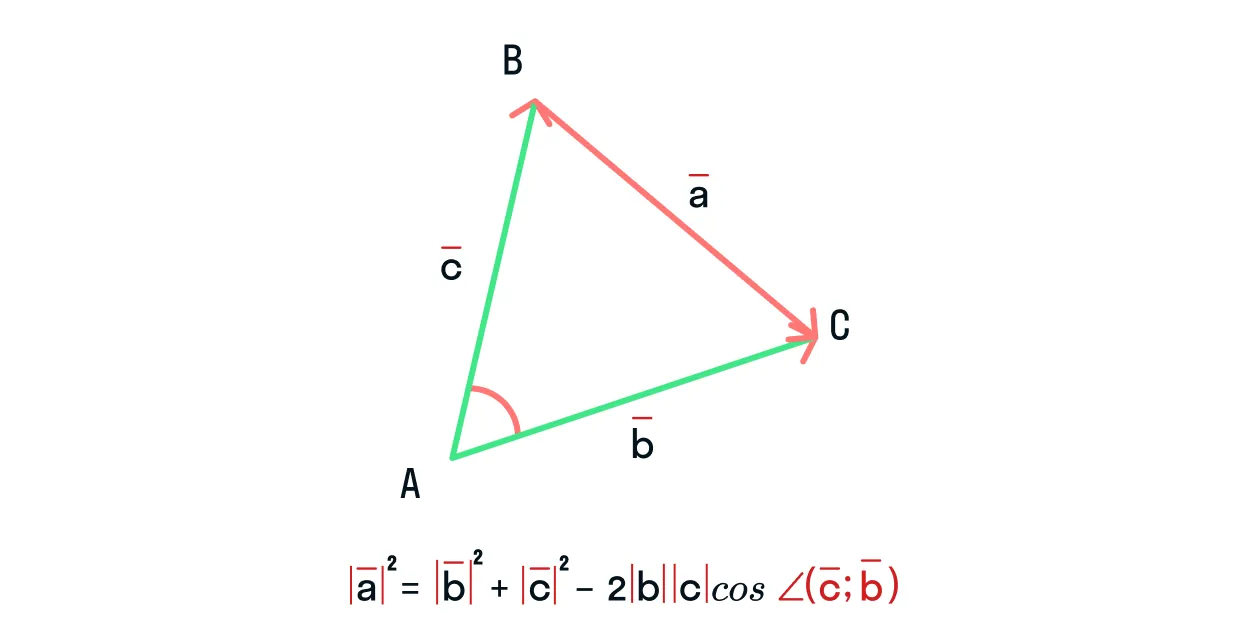
Тогда, чтобы найти длину , необходимо знать (или иметь возможность вычислить) длины и , знать угол между ними, а также уметь рассчитать произведение длин этих векторов.

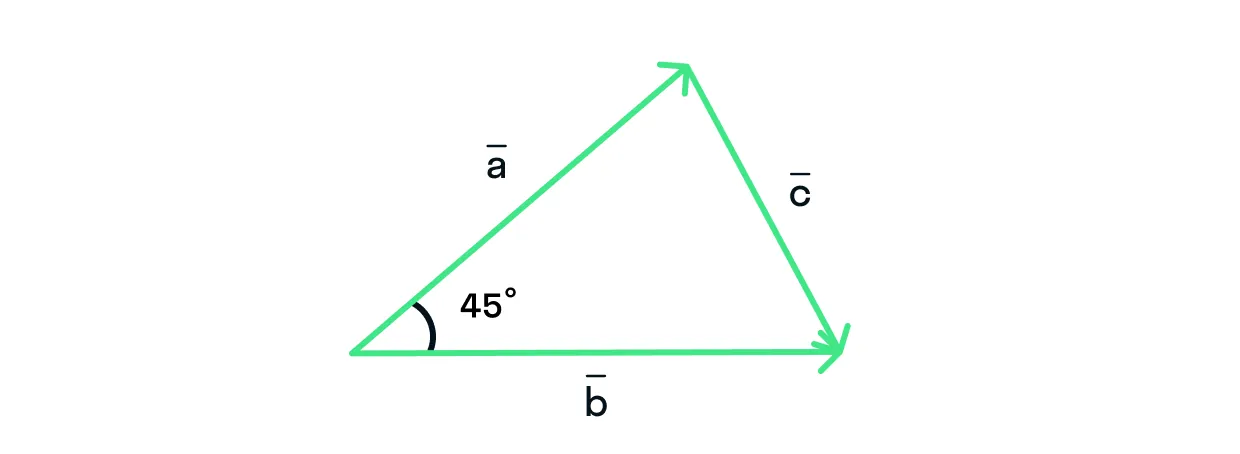
Задача 5

Длины и равны 4 и 6 соответственно, а угол между ними равен Вычислите длину

Решение:

Задача 6

Рассчитайте модуль вектора в треугольнике, если длина = 8, длина = 10, а угол между ними равен

Решение:

Скалярное произведение векторов

Мы практически дошли до финала нашего путешествия по царству векторов. 👑 Нам осталось изучить только скалярное произведение векторов. Что это?

Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.

Скалярным произведением и будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:

Вспомним, что в той же физике величины делятся на скалярные (не имеющие направления, например, масса) и векторные (имеющие направление, например, сила, ускорение, скорость). В математике под вектором подразумевают направленный отрезок, а понятие скаляра хоть и не равно, но очень близко к понятию числа.

Скалярное произведение показывает, насколько синхронизированы, скоординированы направления векторов. Так, чем больше угол между векторами, тем меньше согласованности, а значит, скалярное произведение будет уменьшаться с ростом угла:

• Скалярное произведение вектора на само себя равно квадрату его модуля: В данном случае значение скалярного произведения является наибольшим из возможных.

• Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, так как

  

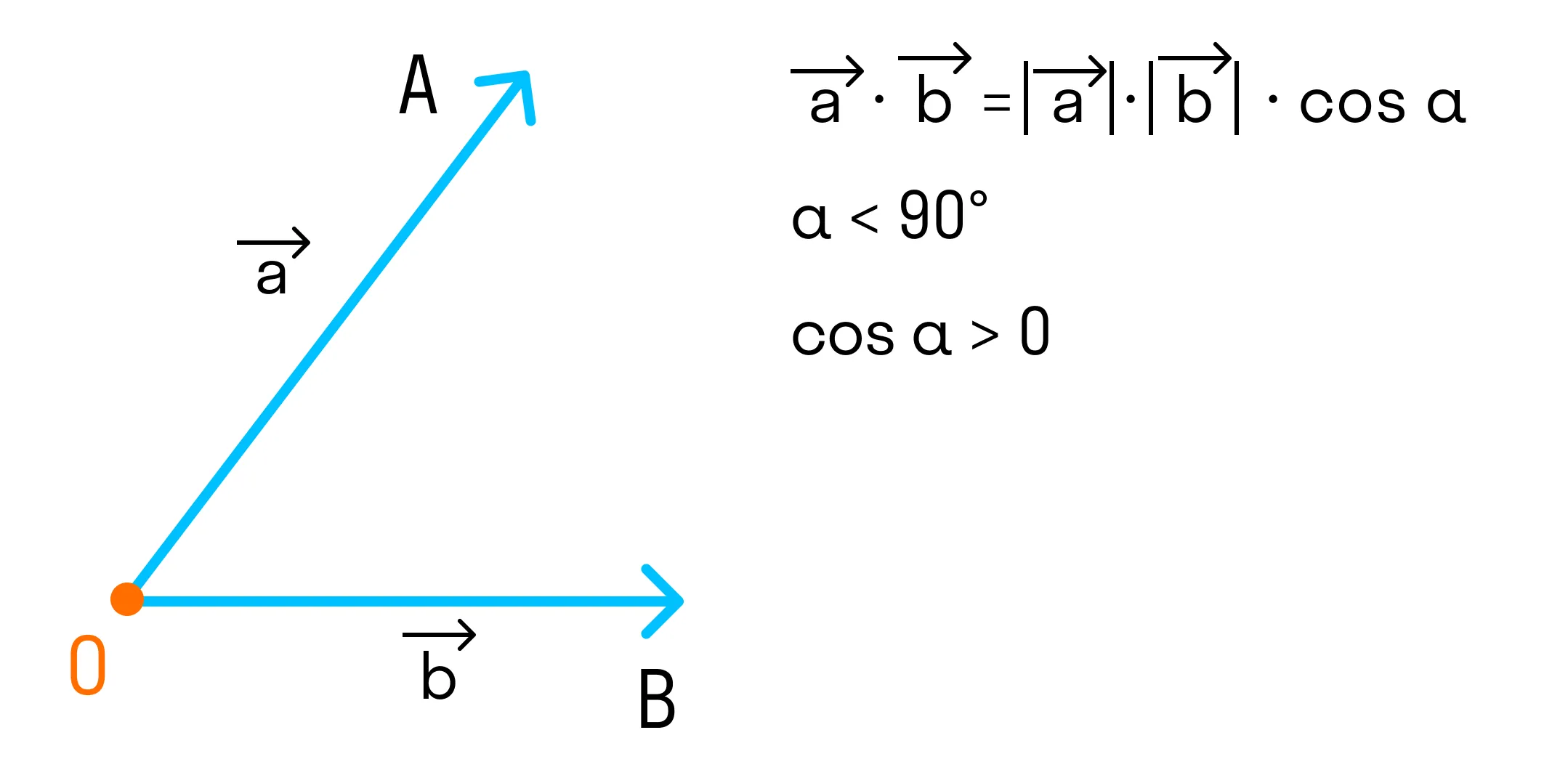
• Если угол между векторами прямой, то скалярное произведение равно 0, так как

  

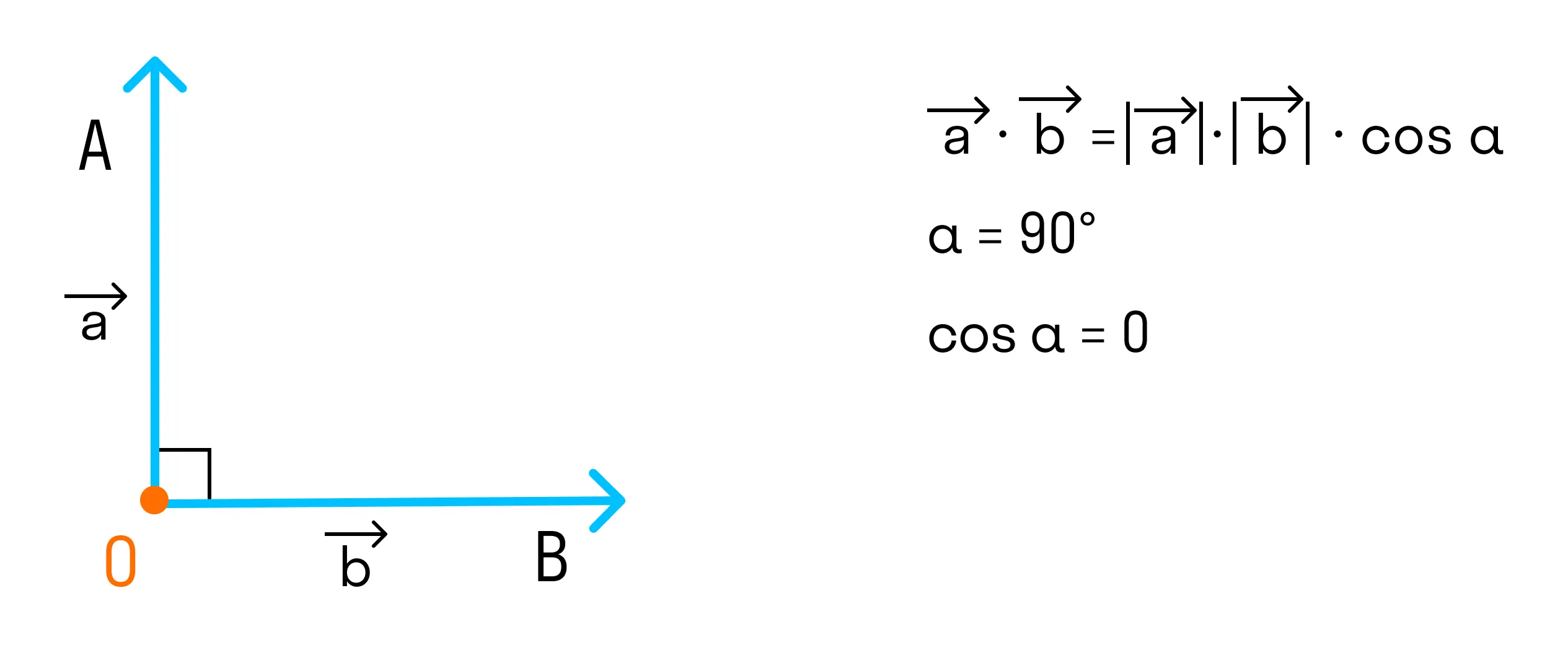
• Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как

  

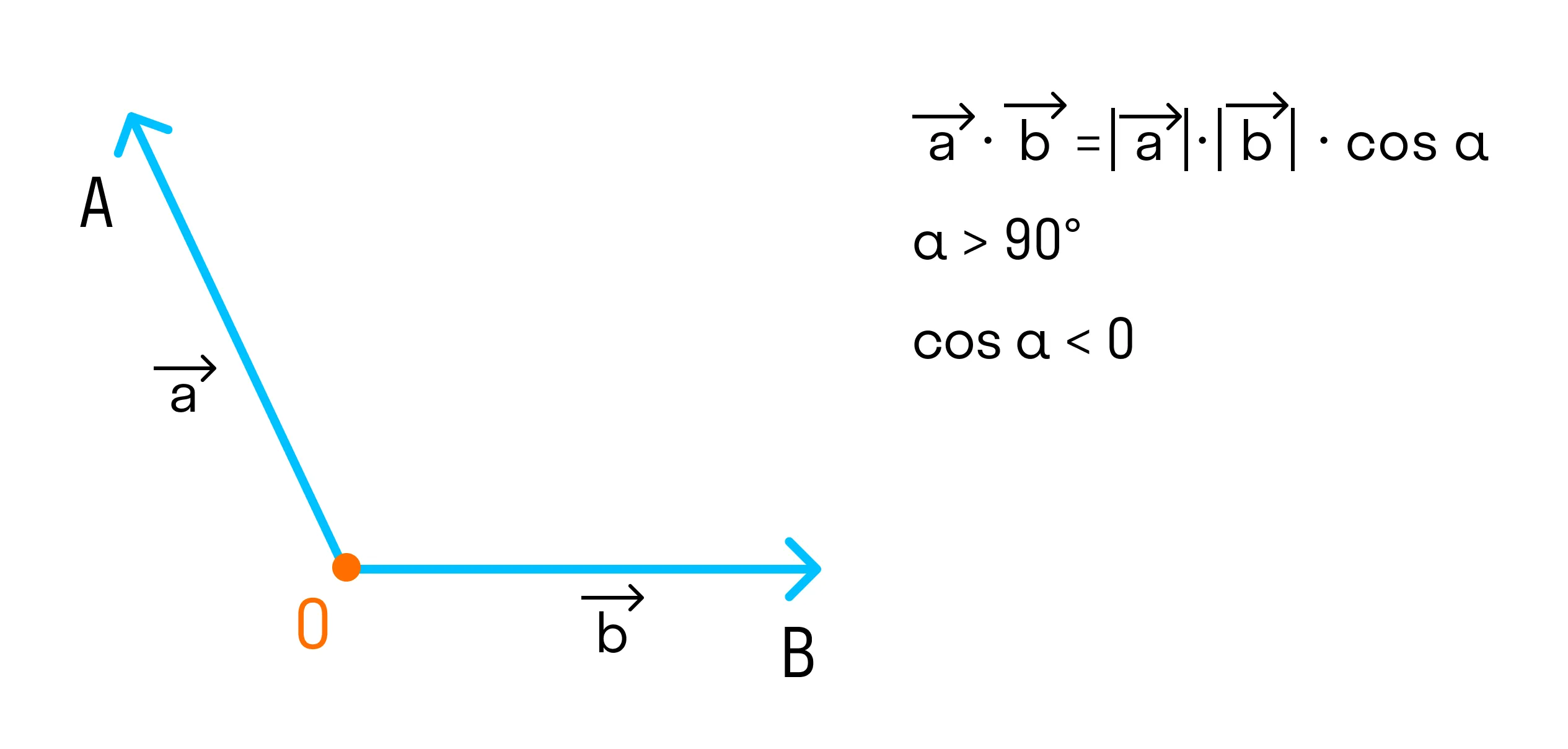
• Cкалярное произведение вектора на противоположно направленный ему вектор равно отрицательному произведению их длин . В данном случае значение скалярного произведения является наименьшим из возможных.

  

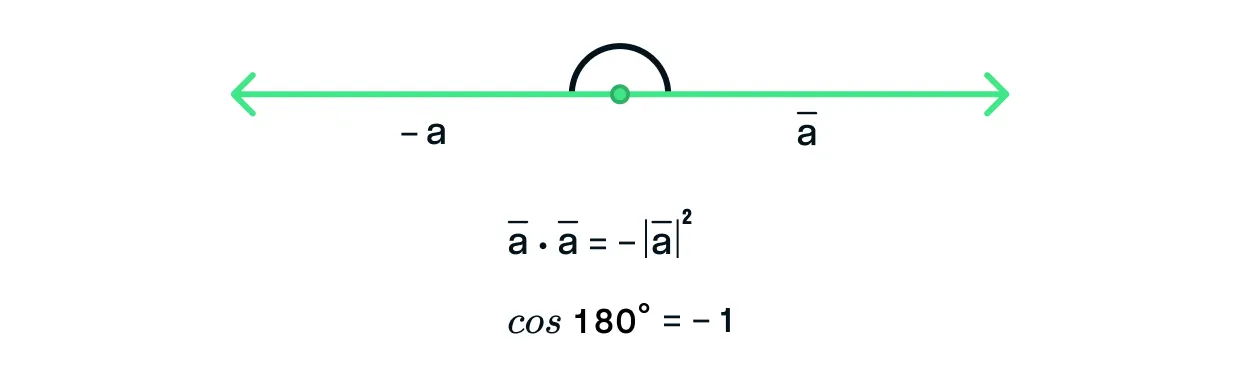
Конечно, вы можете возразить: «Согласованность направлений отлично показывает угол, для чего нам эти сложные вычисления?». А всё дело в том, что в пространстве порой очень сложно измерить угол, а вот посчитать скалярное произведение — просто, особенно если рассмотреть его через координаты.

Если выражен координатами а то скалярное произведение этих векторов описывается формулой: В пространстве скалярное произведение через координаты векторов будет задаваться так:

Где применяется скалярное произведение? Благодаря ему выполняется большое количество математических операций, таких как нахождение угла между векторами и любых расстояний, если они заданы через координаты. Благодаря скалярному произведению можно описать даже характеристику криволинейных поверхностей, но это мы обсудим как-нибудь в другой раз. 🙂

Чтобы закрепить пройденный материал, нужно больше, чем пара заданий. Поэтом приглашаем на онлайн-уроки математики в школу Skysmart. За короткое время благодаря особенной платформе и учителям-профессионалам вы сможете улучшить школьные отметки, подготовиться к экзаменам и олимпиадам, и самое главное — понять и полюбить математику.