Площадь квадрата – это величина, равная произведению длины его сторон.
Формула: S = a², где S – площадь, а a – длина стороны квадрата.
Пример: если сторона квадрата равна 4 см, площадь будет S = 4² = 16 см².
Для кого эта статья:
- Читатели, интересующиеся темой статьи
- Специалисты в данной области знаний
- Студенты или школьники, стремящиеся углубить свои знания
Формула нахождения площади квадрата
Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.
Если известна длина стороны
Умножаем ее на то же число или возводим в квадрат.
S = a × a = a2, где S — площадь, a — сторона.
Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.
Получи больше пользы от Skysmart:
-
Прокачивай знания на курсах математики
-
Выбирай из 1200+ репетиторов по математике
Записывайся на бесплатные курсы для детей
Если нам дана диагональ
Площадь квадрата через диагональ - это квадрат длины диагонали, деленный на два. Формула: S = d² / 2, где S - площадь, d - диагональ.
Например, если диагональ квадрата равна 10 см, то площадь будет S = 10² / 2 = 50 см².
Возводим ее в квадрат и делим на два.
S = d2 : 2, где d — диагональ.
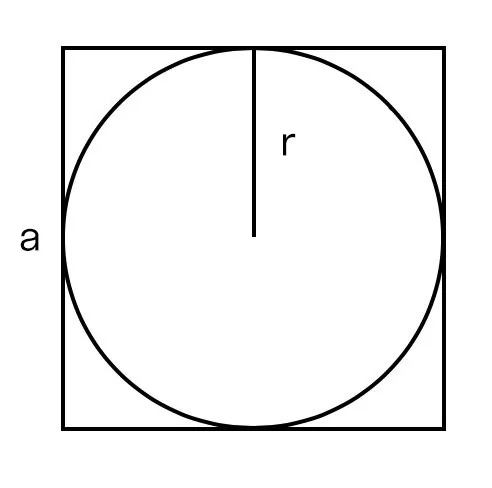
Если известен радиус вписанной окружности
Умножаем его квадрат на четыре.
S = 4 × r2, где r — это радиус вписанной окружности.
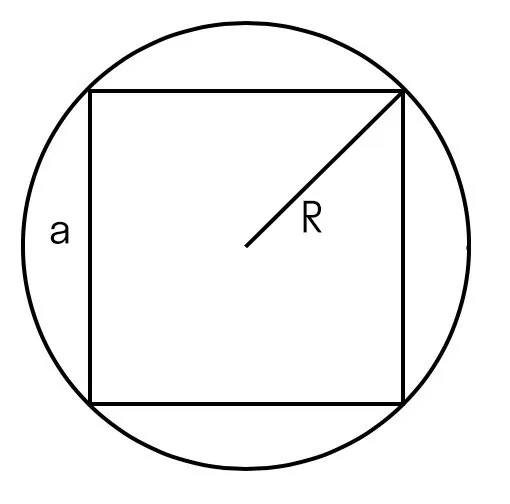
Если у нас есть радиус описанной окружности
Возведем его в квадрат и умножим на два.
S = 2 × R2, где R — это радиус описанной окружности.
|
У нас есть курсы обучения математике для учеников с 1 по 11 классы — записывайтесь! |
Если есть периметр
Мы должны возвести его в квадрат и разделить на 16.
S = Р2 : 16, где Р — это периметр.
Периметр любого четырехугольника равен сумме длин всех его сторон.
Популярные единицы измерения площади:
- квадратный миллиметр (мм2);
- квадратный сантиметр (см2);
- квадратный дециметр (дм2);
- квадратный метр (м2);
- квадратный километр (км2);
- гектар (га).
S квадрата. Решение задач
Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!
Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.
Как решаем:
Воспользуемся формулой: S = d2 : 2.
Подставим в формулу значение диагонали: S = 902 : 2 = 4050 мм2.
Ответ: 4050 мм2.
Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.
Как решаем:
Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
a = dДиаметр окружности равен двум радиусам:
d = 2rПолучается, что сторона равна двум радиусам:
a = 2rИспользуем формулу нахождения площади квадрата через сторону:
S = a2Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
S = (2r)2
S = 4r2Теперь подставим значение радиуса в формулу площади:
S = 4 × 242 = 2304 см2
Ответ: 2304 см2.






















