Возрастание и убывание функции

Что такое функция

Как обычно, начнем мы с самого начала: с определения слова «функция».

Под функцией понимают правило, формулу, уравнение, которое описывает зависимость одной переменной от другой (например, у от х). Если изучить функцию, мы поймем:

• как изменится одна переменная, если другая увеличится;

• что произойдет с аргументом, если мы уменьшим функцию;

• что будет, если мы отобразим эту зависимость графически.

Спойлер: если изобразить зависимость в координатной системе, мы получим график! Давайте рассмотрим некоторые виды функций и графики, которые им соответствуют.

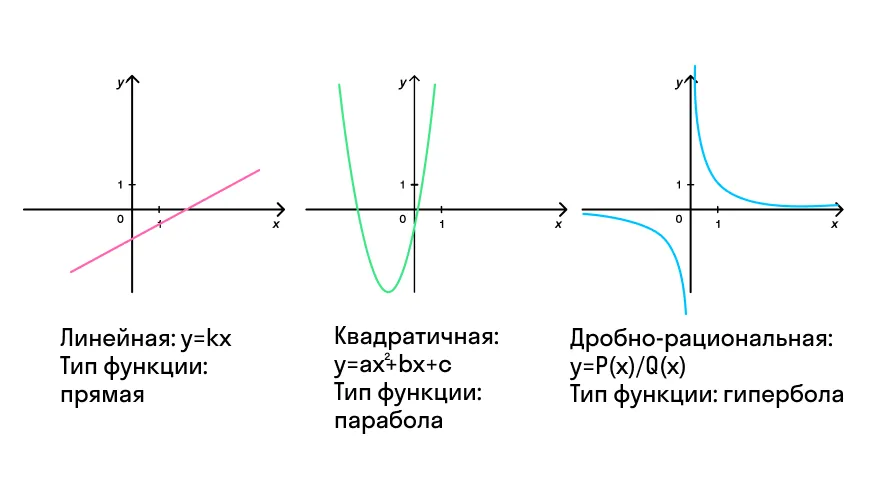
Важное напоминание: функция — это зависимая переменная величина (чаще у), аргумент — независимая переменная (чаще х).

Соглашаюсь на обработку персональных данных в соответствии с условиями пользовательского соглашения

← Далее →

Скачать

Modal window id: popup-professionsbox

Возрастание и убывание функции

В исследовании функции особое значение уделяют ее поведению в системе координат — монотонности функции. Функции бывают монотонными, немонотонными и постоянными.

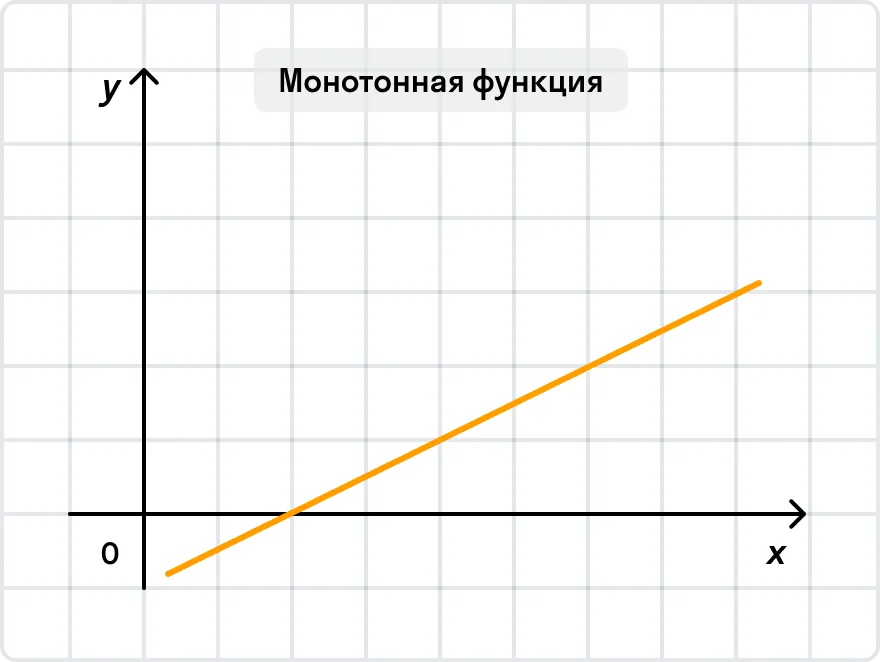
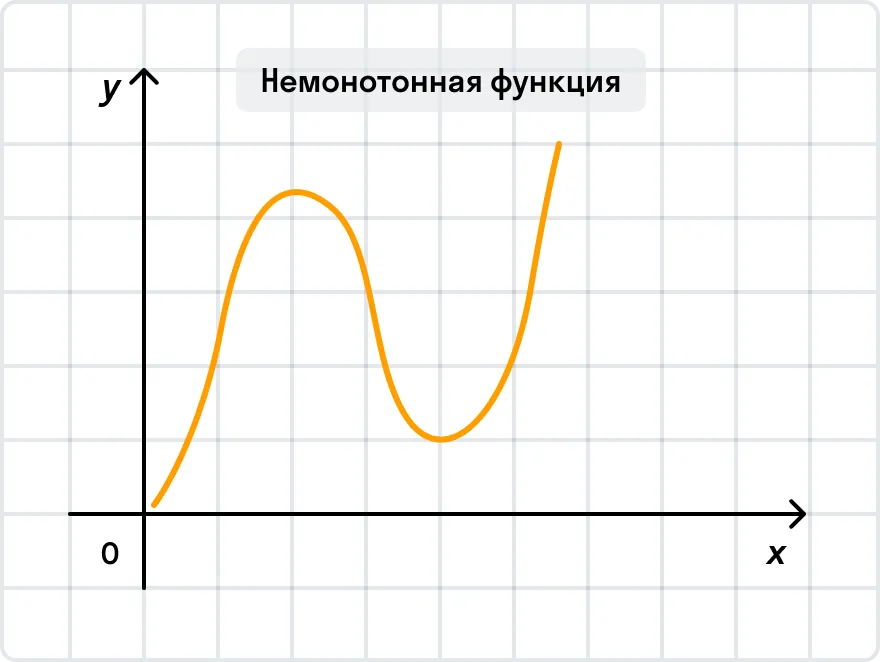
Теперь к теме раздела: приведем определение возрастающей и убывающей функции.

Проще говоря, здесь работает правило «чем больше, тем больше»: чем больше значение х, тем больше и значение у.

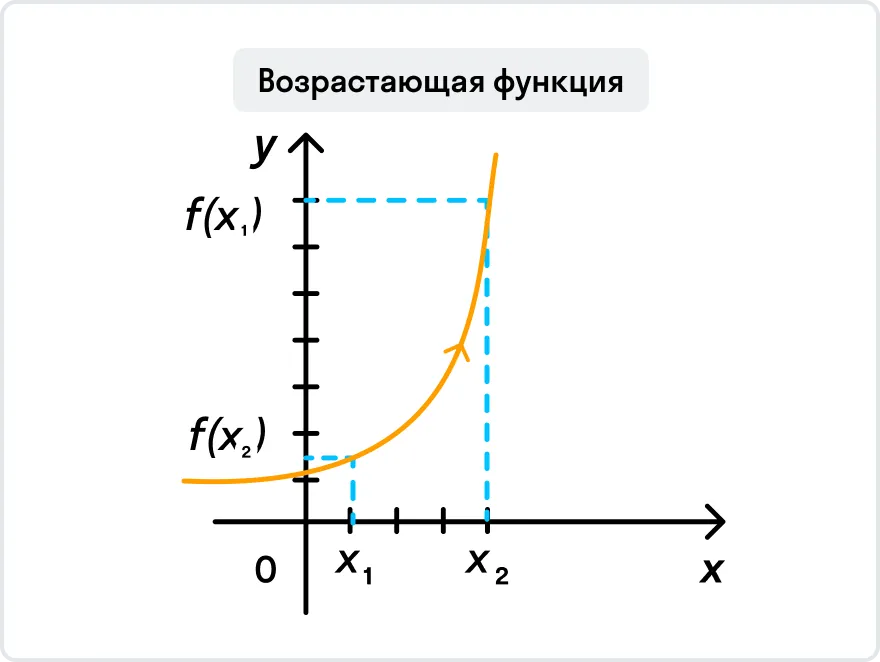
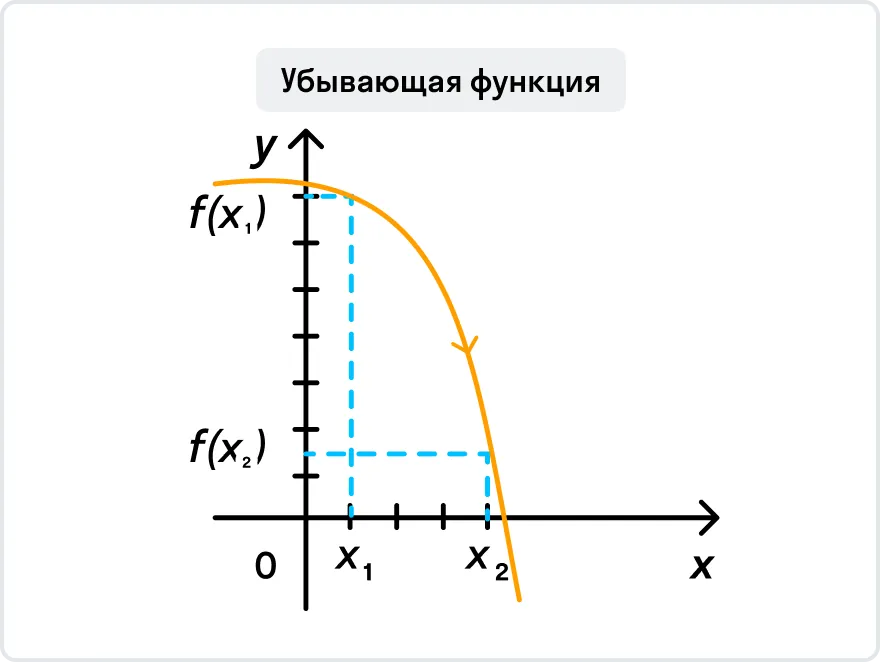
Теперь вы знаете, как понять, что функция возрастает или убывает. Давайте решим пару задач, чтобы разобраться во всем наглядно.

Задача 1

Определите, возрастающая или убывающая функция y = 2x + 3.

1) Найдем область определения функции: х ∈ R.

2) Найдем координаты нескольких точек, которые ей принадлежат.

Как вы уже заметили, значения х и у одновременно увеличиваются — функция возрастает на всем промежутке.

Задача 2

Определите, возрастающая или убывающая функция y = 1/2х.

1) Найдем область определения функции: х ≠ 0.

2) Найдем координаты нескольких точек, которые ей принадлежат.

Мы видим, что функция убывает при любом значении х ≠ 0. Это можно записать так: функция убывает при х∈ (– ∞ ;0) ∪ (0; + ∞). Подытожим эту информацию небольшой схемой.

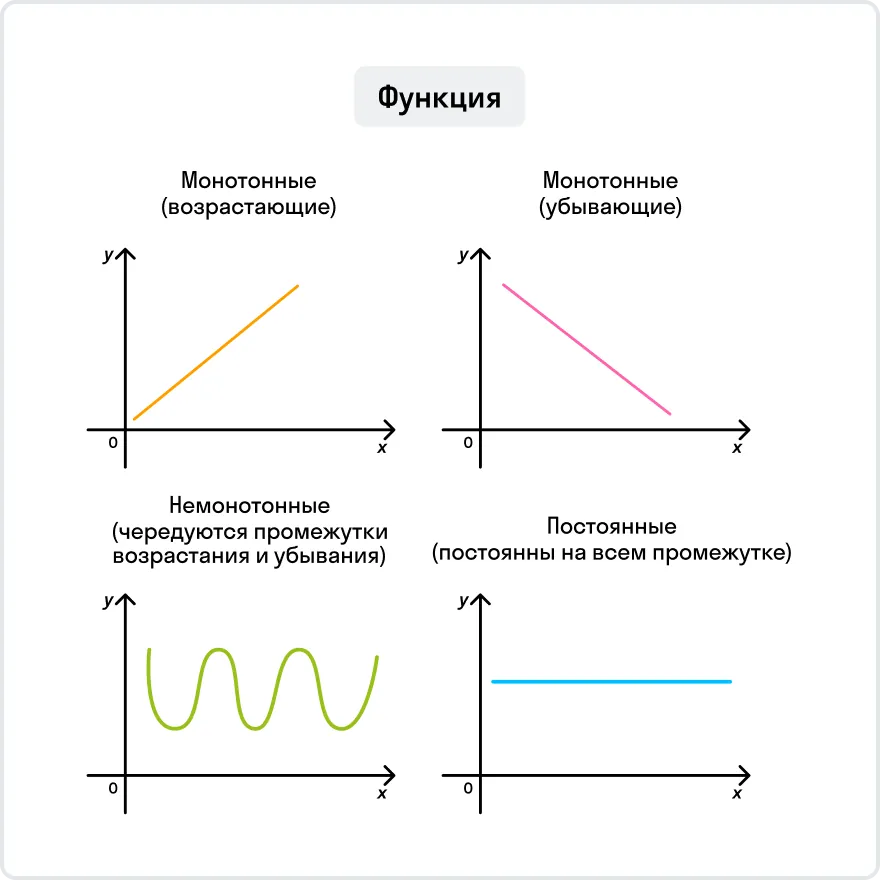
Возрастание и убывание функции на интервале

Мы еще не закончили с возрастающими и убывающими функциями — эх, если бы все было так просто! Дело в том, что нас, математиков, интересуют вот какие вопросы:

• Как найти промежутки возрастания и убывания функции по графику?

• Что делать, если просят определить характер на числовом промежутке?

• Как определить поведение функции без построения?

Давайте разбираться! Сначала узнаем, как определить характер функции на промежутке:

• Подставим значение х из промежутка в функцию.

• Проанализируем полученные значения у.

• Если при увеличении х увеличивается и у — это промежуток возрастания функции.

• Если у уменьшается при увеличении х — это промежуток убывания функции.

Достаточно просто, правда? :)

Пример

Возьмем функцию y = 4x – 6 и определим ее характер на промежутке [0;2]. Подставим числа из промежутка вместо х в функцию:

Мы видим, что при возрастании х возрастает и значение у, т. е. на этом промежутке функция возрастает.

Точки экстремума, экстремумы функции

Не пугайтесь этих страшных слов! Сейчас разберем их подробнее — это проще, чем кажется.

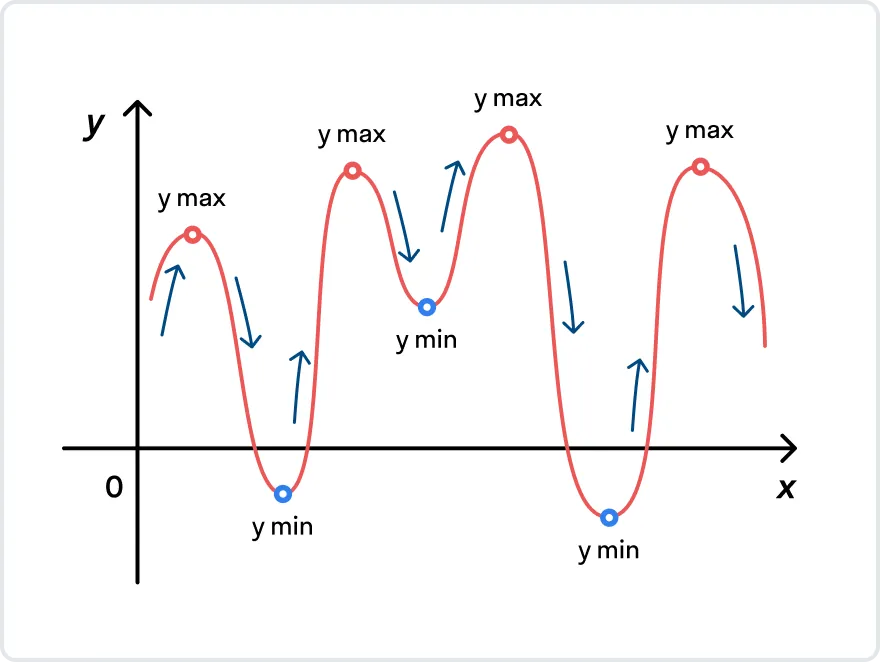
На графике выше y min — минимальное значение функции, точка минимума.

На том же графике y мах — максимальное значение функции, точка максимума.

Иначе точки минимума и максимума в математике принято называть точками экстремума, а значения функции, которые соответствуют точкам экстремума — экстремумами функции.

В точках экстремума функция меняет свой характер. Обратите внимание на рисунок ниже: функция стремительно возрастала до точки максимума, но после нее начала также стремительно уменьшаться. И наоборот, после прохождения точки минимума функция снова начинает возрастать.

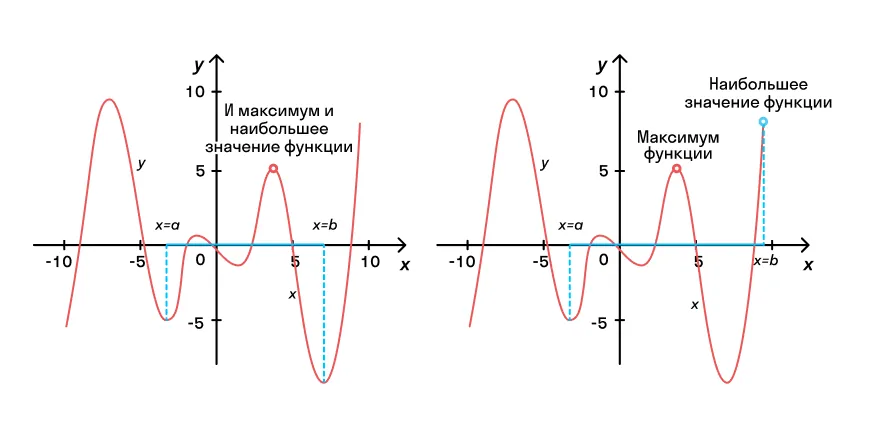
Здесь вам может стать интересно: наибольшее/наименьшее значение функции на промежутке — это то же самое или нет. Отвечаем: к сожалению, нет. Эти значения иногда могут совпадать, но часто определяются разными точками.

170.4K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Прокачивай знания на курсах математики.

• Выбирай из 1200+ репетиторов по математике.

• Записывайся на бесплатные курсы для детей.

Достаточные условия возрастания и убывания функции

У нас есть две новости: хорошая и не очень. Начнем с первой: если использовать достаточные условия возрастания/убывания, можно определить промежутки монотонности функции. И для этого даже не придется строить график! Но здесь нам пригодится производная.

Иначе говоря, производная функции показывает, как быстро увеличивается функция при бесконечно малом увеличении х.

К сожалению, в рамках этой статьи мы не будем долго останавливаться на производных. Как это сделать с помощью таблицы и правил дифференцирования, мы уже разбирали в статье «Таблица производных функций». Советуем почитать!

Достаточные признаки возрастания и убывания функции на интервале:

• если производная функции y = f(x) положительна для любого x из интервала, то функция возрастает на этом интервале;

• если производная функции y = f(x) отрицательна для любого x из интервала, то функция убывает на этом интервале.

Составим алгоритм действий, который поможет найти интервалы возрастания и убывания функции:

1. Найдем область определения функции.

2. Найдем производную функции.

3. Решим неравенства ƒ`(x) > 0 и ƒ`(x) < 0 на области определения.

4. К полученным промежуткам добавим граничные точки, в которых функция определена и непрерывна.

5. Проверим достаточные признаки возрастания и убывания функции, подставив значения из промежутков.

Задача 3

Укажите промежутки возрастания и убывания функции у = х² + 5х + 6

Решение

1. Область определения функции: х ∈ R

2. Найдем производную функции: y’ = 2х + 5

3. Решим неравенство: 2х + 5 > 0

   2х+5 >0
   2x>-5
   x> –2,5

4. Исследуем знаки производной с помощью числовой прямой.

   

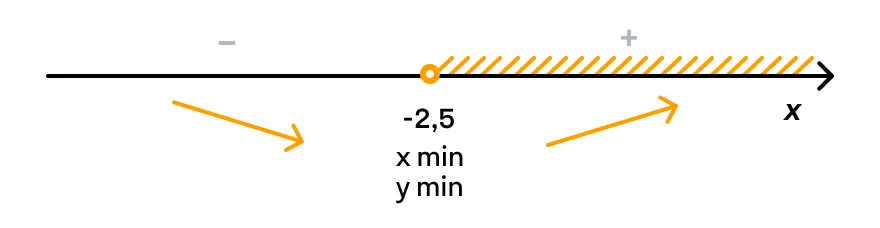
Ответ: Функция убывает при х∈ (– ∞; –2,5], возрастает при х∈ [–2,5; +∞)

Задача 4

Определите интервалы возрастания и убывания функции у = х³ – 18х.

Решение

1. Область определения функции: х ∈ R.

2. Найдем производную функции: y’ = 3x² + (–18).

3. Решим неравенство:

   3x² + (–18) > 0
   3 (x²–9) > 0
   3(x – 3)(x + 3) > 0

4. Исследуем знаки производной с помощью числовой прямой. Чтобы определить знак на каждом промежутке, подставим произвольное значение из этого промежутка в выражение для производной.

   

Ответ: Функция убывает при х∈ [–3;3], возрастает при х∈ (–∞;—3] ∪ [3; +∞).

Первое достаточное условие экстремума

Пусть для функции у = f(x) определены следующие условия:

1. Функция непрерывна в окрестности точки x0 (нет разрыва).

2. ƒ′(x0) = 0 или ƒ′(x0) не существует;

3. Производная ƒ′(x) при переходе через точку x0 меняет свой знак.

Тогда в точке x = x0 функция y = f(x) имеет экстремум, причем это минимум, если при переходе через точку x0 производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку x0 производная меняет свой знак с плюса на минус.

Если производная в точке x0 не меняет свой знак, то в этой точке нет экстремума.

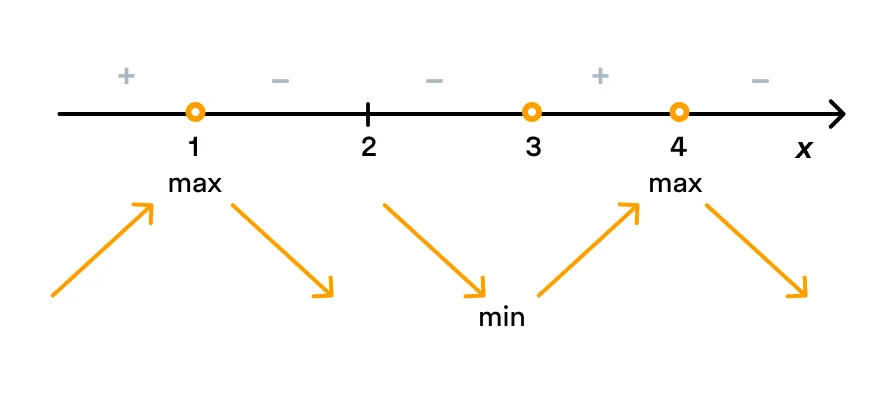
Итак, точки 1 и 4 — точки максимума, точка 3 — точка минимума. В точке 2 экстремума нет.

Алгоритм для нахождения точек экстремума

Теперь разберемся, как найти точки экстремума функции. Для этого пройдем по этим шагам:

1. Найдем область определения функции.

2. Найдем производную функции на этой области.

3. Определим нули и точки, где функция не существует.

4. Определим знак производной на интервалах.

5. Выберем точки, где функция меняет знак.

6. Найдем точки минимума/максимума и экстремумы функции.

Задача 5

Найдите экстремумы функции у = –x² + 8x – 7.

Решение

1. Область определения функции: х ∈ R.

2. Производная функции: y’ = –2x + 8

3. Решим неравенство:

   –2x + 8 > 0
   –2x > –8
   x < 4

4. Определим знак производной на числовой прямой. Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.

   

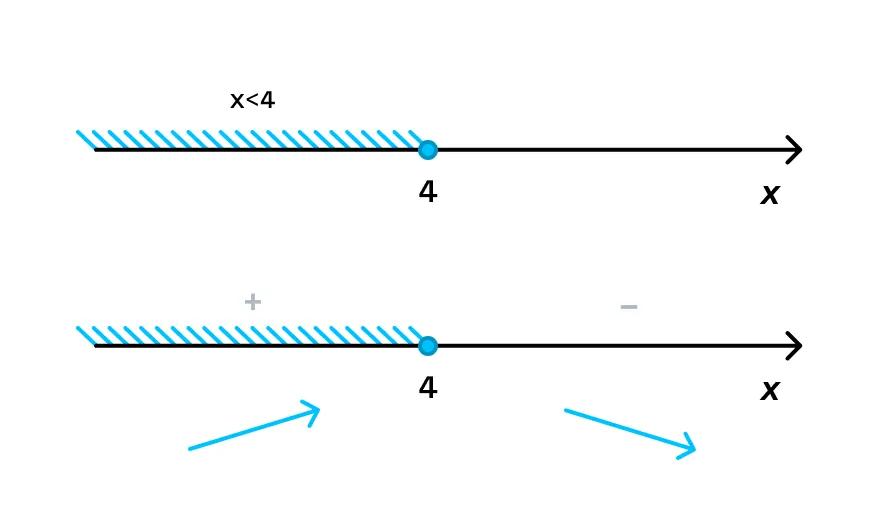
В точке х = 4 функция меняет свой знак с «+» на «–», значит, точка х = 4 — это точка максимума.

Ответ: у(4) = 9 — экстремум функции.

Задача 6

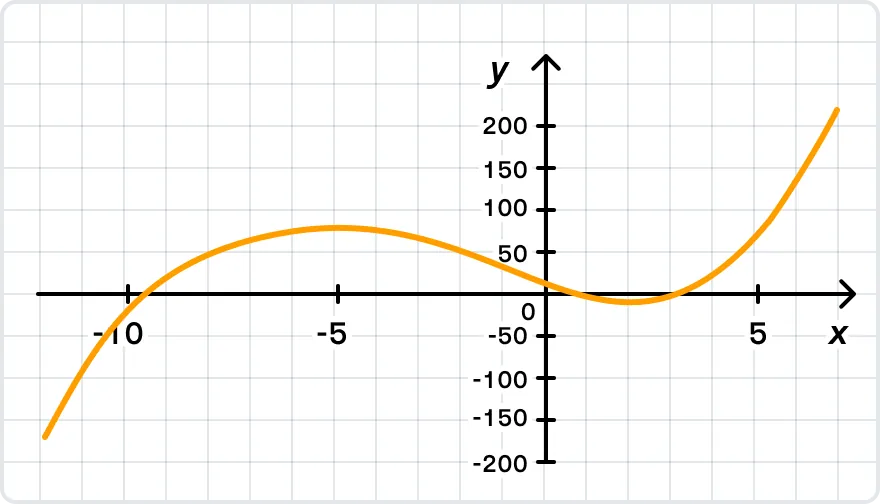
Найдите экстремумы функции у = ⅓ x³ + 2x² – 12x + 6.

Решение

1. Область определения функции: х ∈ R.

2. Производная функции: y’ = x² + 4x – 12.

3. Решим неравенство:

   x² + 4x – 12 > 0
   (x – 2)(x + 6) > 0

4. Определим знак производной на числовой прямой. Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.

   

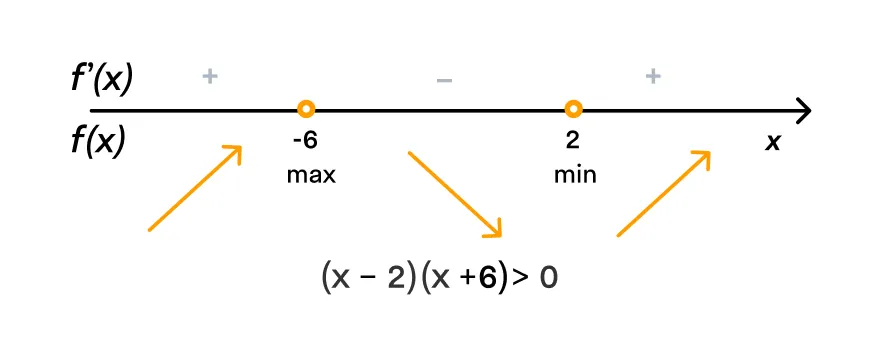
Так на интервале (–∞; –6) и (2; +∞) производная положительна — на них функция возрастает. На интервале (–6;2) производная отрицательна — функция убывает.

Ответ: x = 2 — точка минимума, у(2) = –7 ⅓ — экстремум функции; х = –6 — точка максимума, у(–6) = 78 — экстремум функции.

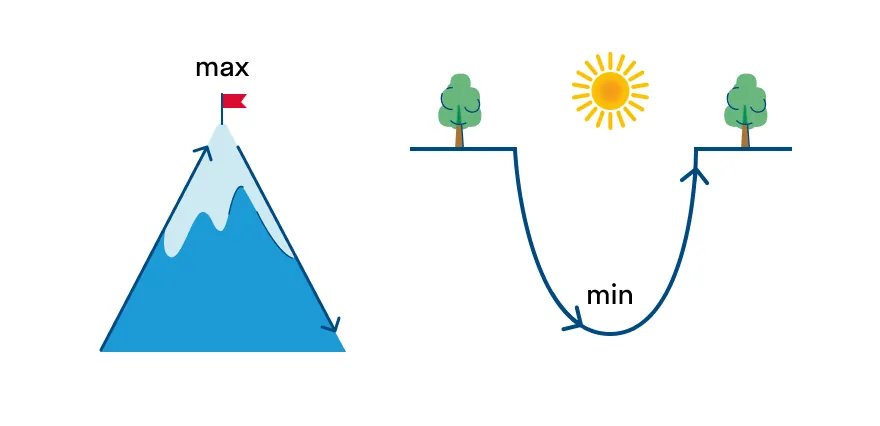
Как можно запомнить переход знаков для точек максимум или минимум:

• Когда функция возрастает, а потом убывает, мы будто поднимались на вершину горы — значит, посетили точку максимума.

• Когда функция убывает, а потом возрастает, мы будто спускались в овраг и выбрались из него — а значит, были в точке минимума.

Второе достаточное условие экстремума

x₀ — это точка экстремума функции f(x), если вторая производная функции в этой точке не равна нулю (f ''(x) ≠ 0). Причем, если вторая производная больше нуля (f ''(x) > 0), то точкой минимума, а если вторая производная меньше нуля (f ''(x) < 0), то точкой максимума.

Рассмотрим это условие экстремума на примере из задачи 6 — функции у = ⅓ x³ + 2x² – 12x + 6:

1. Ее первая производная равна y’= x² + 4x – 12.

2. Определим нули производной — значение х, при котором производная обращается в ноль: x^{2 + 4x – 12 = 0 при х = 2 и х = –6.}

3. Возьмем вторую производную функции y’’= 2х + 4.

4. Подставим значения х = 2 и х = –6 во вторую производную и определим, являются ли эти точки максимумом или минимумом:

   y’’(2) = 8, y’’ > 0, значит, х = 2 является точкой минимума,
   y’’(–6) = –8, y’’ < 0, значит, х = –6 является точкой максимум.

В этом условии есть два важных замечания:

1. Если в точке x0 и первая, и вторая производные обращаются в ноль, то в этом случае нужно воспользоваться первым достаточным признаком экстремума функции, по второму признаку нельзя судить о наличии или отсутствии экстремумов.

2. Второй достаточный признак нельзя применять, когда в стационарной точке (нуле производной) первая производная не существует. Ведь тогда не существует и вторая производная.

Третье достаточное условие экстремума

Это условие не используется в школьной программе, так как требует большого количества вычислений и логических размышлений. Мы все равно познакомим вас с ним — возможно, вам захочется изучить это усaловие самостоятельно и блеснуть знаниями перед учителем. Что ж, мы только за!

Пусть функция y=f(x) имеет производные до n-ого порядка в ε-окрестности точки x0 и производные до n+1-го порядка в самой точке x0. Пусть ƒ′(x₀) = ƒⁿ(x₀) = ƒ^m(x₀) = … = ƒ⁽ⁿ⁾(x₀) = 0 и ƒ⁽ⁿ⁺¹⁾(x₀) ≠ 0.

Тогда,

• если n – четное, то x₀ — точка перегиба;

• если n – нечетное, то x₀ — точка экстремума, причем

• если ƒ⁽ⁿ⁺¹⁾(x₀) > 0, то x₀ — точка минимума;

• если ƒ⁽ⁿ⁺¹⁾(x₀) < 0, то x₀ — точка максимума.

Думаем, вы убедились, что тема «Возрастание и убывание функции» достаточно интересна. В то же время, она требует умения исследовать графики, находить первую и вторую производную функции, определять знаки по числовым прямым. Получить практический опыт решения таких заданий можно на курсах по профильной математике в школе Skysmart! Там мы сможем закрепить полученные знания, подготовиться к контрольным работам и даже к ОГЭ! Заинтригованы? Тогда мы ждем вас на занятиях!