Коллинеарность векторов

Ученики 9-го класса, помимо понятия вектора, должны знать, что такое коллинеарные векторы, а также условия коллинеарности векторов.

Вектор — это направленный отрезок. Вектор обозначается двумя заглавными латинскими буквами со стрелочкой над ними или одной маленькой со стрелочкой над ней .

Нулевой вектор — вектор, начало которого совпадает с концом. То есть в геометрической интерпретации это просто точка.

Теперь, когда мы вспомнили базовые понятия, можно переходить к определению коллинеарных векторов.

Что значит «коллинеарные векторы»

Коллинеарные векторы — это ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Причем считается, что нулевой вектор коллинеарен каждому другому вектору. То есть, попросту говоря, коллинеарность — это параллельность векторов. Если векторы и коллинеарны, то это записывают так: .

Коллинеарные векторы можно разделить по направлению на две группы: сонаправленные и противоположно направленные.

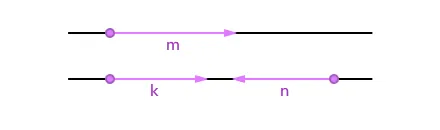
Векторы и лежат на параллельных прямых, а также имеют одно направление, поэтому и — сонаправленные векторы: .

Векторы и лежат на параллельных прямых, но имеют разное направление, поэтому и — противоположно направленные векторы: .

Задача № 1

Найдите сонаправленные и противоположно направленные векторы.

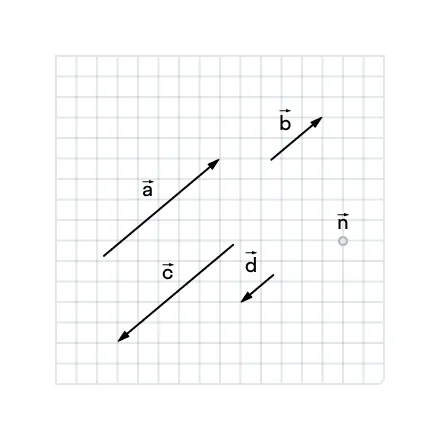
Благодаря клетчатому фону мы можем определить, что все векторы на рисунке коллинеарны, то есть лежат на параллельных прямых. Осталось посмотреть на направление векторов и сделать выводы:

• ,

• ,

• ,

• .

Но не забываем о нулевом векторе — он будет сонаправлен с каждым вектором.

Но согласитесь, что визуальная оценка параллельности не самая точная вещь на планете, а математика славится своей точностью и четкостью. Поэтому возникает вопрос: как проверить коллинеарность векторов алгебраическими способами? Для этого существуют признаки коллинеарности векторов. Рассмотрим их.

Признаки коллинеарности векторов

1. Первый критерий коллинеарности векторов: векторы и коллинеарны, если .

2. Второй критерий коллинеарности векторов: два вектора коллинеарны, если отношения их координат равны.

   Но здесь важно понимать, что это условие параллельности векторов работает только для всех ненулевых координат. Значит, если хотя бы один компонент вектора равен нулю, то правило неприменимо.

3. Третий критерий коллинеарности векторов, который могут применять одиннадцатиклассники, взрослые и все, кто увлечен математикой: два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

Применим условия коллинеарности векторов при решении задач.

Задача № 2

Докажите, что векторы и коллинеарны.

У нас с вами есть два способа определить или доказать коллинеарность векторов, однако в координатах каждого вектора есть нули — значит, подходит только первый критерий, который еще называется свойством коллинеарных векторов: если , то .

Для начала определим . А теперь проверим, выполняется ли условие :

, значит, . Что и требовалось доказать.

Задача № 3

Какие из векторов , и коллинеарны?

А здесь очень удобно использовать второй критерий коллинеарности векторов, который звучит так: отношения соответствующих координат коллинеарных векторов равны.

1. Проверим коллинеарность векторов и : должно выполняться условие , т. е. — верно, значит, .

2. Проверим коллинеарность векторов и : должно выполняться условие , т. е. — неверно, значит, и неколлинеарны.

3. Проверим коллинеарность векторов и : должно выполняться условие , т. е. — неверно, значит, и неколлинеарны.

Задача № 4

Определите, при каком значении k векторы и коллинеарны.

Так как по условию векторы должны быть коллинеарны, а в их координатах не содержится нуля, то можно использовать второй критерий коллинеарности, а именно — должно выполняться условие , то есть .

По свойству пропорции выразим k:

;

k = 27.

Значит, при k = 27 векторы и коллинеарны.

Если же вам нужно проверить коллинеарность векторов в пространстве, а не на плоскости, то все эти условия продолжают работать, но помните, что к проверке присоединяется третья координата векторов. Рассмотрим пару примеров.

Задача № 5

Докажите, что векторы и коллинеарны.

Поступим аналогично решению в задаче 2 — применим первый критерий, который еще называется свойством коллинеарных векторов, т. е. если , то .

Для начала определим . А теперь проверим, выполняется ли условие :

, значит, . Что и требовалось доказать.

Задача № 6

Определите, при каких значениях k и f векторы и коллинеарны.

Аналогично задаче 4: так как по условию векторы должны быть коллинеарны и в их координатах не содержится нуля, то можно использовать второй критерий коллинеарности. А именно — должно выполняться условие , то есть .

Рассмотрим первую и вторую дроби, по свойству пропорции выразим k:

;

k = 27.

Рассмотрим первую и третью дроби, по свойству пропорции выразим f:

;

f = 2.

Значит, при k = 27 и f = 2 векторы и коллинеарны.

Векторы — удивительная тема, с помощью которой можно решить многие физические задачи, легко и просто доказать самые сложные геометрические теоремы. Сегодня вы узнали, какие векторы называются коллинеарными, но это лишь один аспект большой главы о векторах. Чтобы узнать остальные действия с векторами, познакомиться с интересными задачами и способами решений, приходите на онлайн-курсы математики для детей в Skysmart.