Нахождение наибольшего и наименьшего значения функции

Практикуйся по этой теме! Пройди задание №12 ЕГЭ по профильной математике

В этой статье мы разберём нахождение наибольшего и наименьшего значения функции на отрезке, интервале, в бесконечности, а также повторим основные свойства функции и связанные термины.

Что такое функция

Наш мир — это огромная коллекция взаимосвязей, которые порой явно, а порой невидимо влияют на всех, кто в них участвует. Ваше настроение может влиять на успеваемость в школе, питание — на спортивные достижения, навыки — на возможность поступить в университет. В физическом мире температура влияет на скорость протекания процесса, плотность тела — на его способность к плаванию в воде, угол падения лучей — на то, каким образом они будут преломляться, пройдя через прозрачную призму.

Некоторые из этих взаимоотношений можно описать математически: обозначить участников буквами латинского алфавита и описать их взаимосвязь через математические действия и знаки.

Функция — это правило, формула или выражение, которое описывает взаимосвязь двух величин.

Как описать зависимость пройденного пути от времени?

Есть ли правило, которое описывает отношение ускорения тела и силы, приложенной к нему? Да:

А что, если нужно вычислить зависимость остатка денег от количества купленных товаров? Пожалуйста: , где — остаток денег, — исходная сумма, — количество товара, — стоимость товара за одну единицу.

В каждом из этих выражений есть зависимая и независимая переменные. Зависимая переменная — это и есть функция, а независимая — аргумент. Так, в нашем последнем примере стоимость товара за одну его единицу является независимой переменной (цену назначил продавец, и мы на это повлиять никак не можем). Зато остаток в кошельке поддаётся изменениям — чем меньше мы купим товара, тем больше останется денег. И так в любой зависимости!

Графическое задание функции

Представьте, что для школьной научной конференции вы готовите доклад о загрязнении окружающей среды. Как вы думаете, что произведёт больший эффект на аудиторию:

• перечисление статистических данных об увеличении количества мусора за последний год;

• наглядная демонстрация роста загрязнений в виде графика?

Верно — иллюстрации, фотографии, графики и диаграммы говорят порой громче любых слов! 📈

Для наглядного отображения зависимости одной переменной от другой мы введём систему координат, в которой построим график. График — это прямая, кривая или ломаная линия, которая была построена чётко по уравнению (функции).

Как мы уже говорили, функция состоит из зависимой и независимой переменной. В декартовой системе координат независимая переменная отображается с помощью оси зависимая — с помощью оси

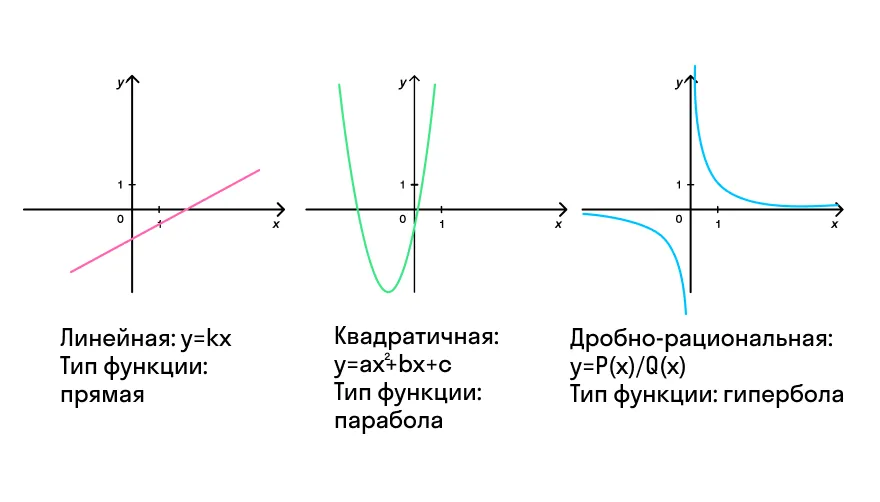
В зависимости от типа функции график может выглядеть, например, так:

170.4K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Наибольшее и наименьшее значение функции

На уроках алгебры учитель просит определить наибольшее и наименьшее значение функции. Что он имеет в виду?

Чтобы найти наименьшее или наибольшее значение функции, необходимо понять, какое наименьшее или наибольшее численное значение принимает — зависимая переменная.

Наибольшее значение функции на некотором промежутке — это значение которое при любом значении делает справедливым неравенство

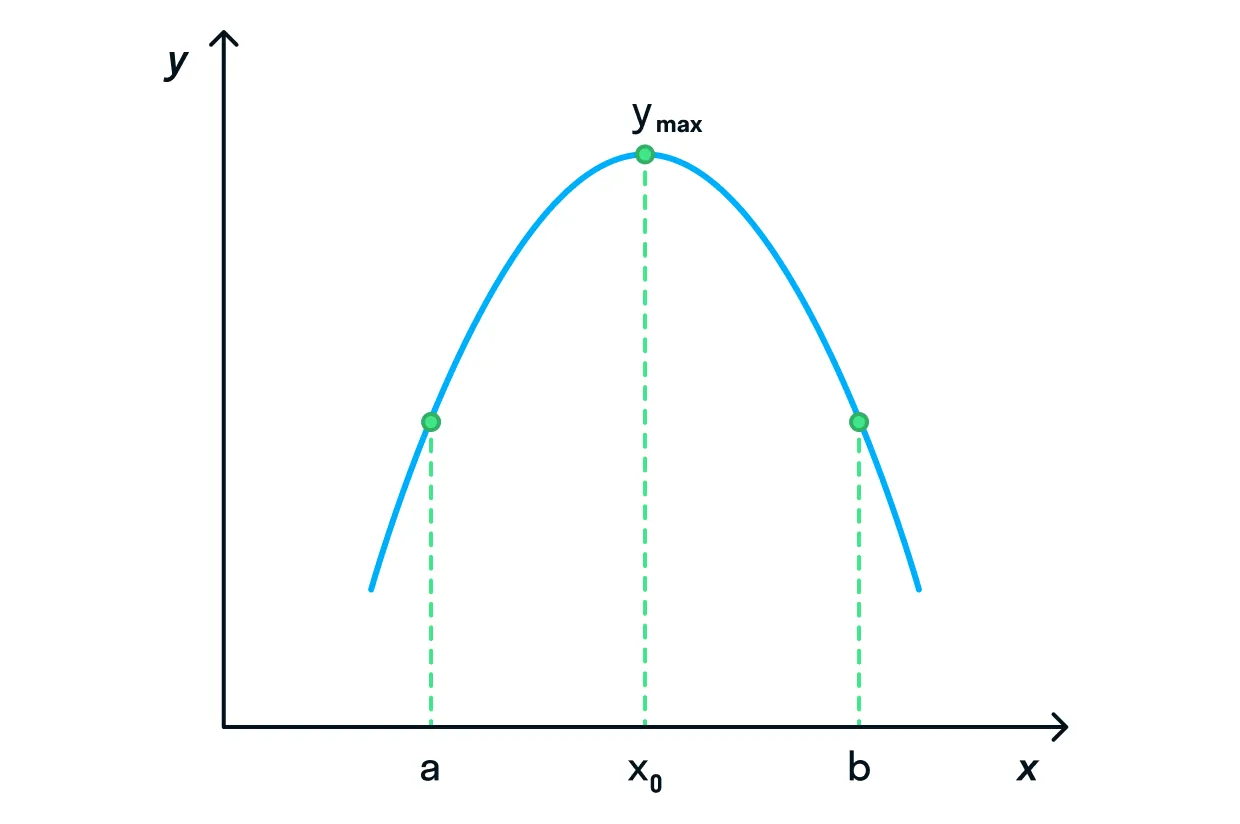
Теперь расшифровка! 😅 Если на данном интервале значение больше, чем значение в окрестностях точки то такой будет считаться наибольшим значением на данном промежутке.

Наименьшее значение функции на некотором промежутке — это значение которое при любом значении делает справедливым неравенство

Если на данном интервале значение меньше, чем значение в окрестностях точки то такой будет считаться наименьшим значением на данном промежутке.

Наибольшее и наименьшее значение функции на графиках

Самый простой способ определить и — рассмотреть график.

Если заданный интервал представлен прямой:

• при возрастающей функции: наименьшее значение функция примет при наименьшем аргументе и наоборот, наибольшее значение функции будет соответствовать наибольшему значению аргумента;

• при убывающей функции: наименьшее значение функция примет при наибольшем аргументе и наоборот, наибольшее значение функции будет соответствовать наименьшему значению аргумента.

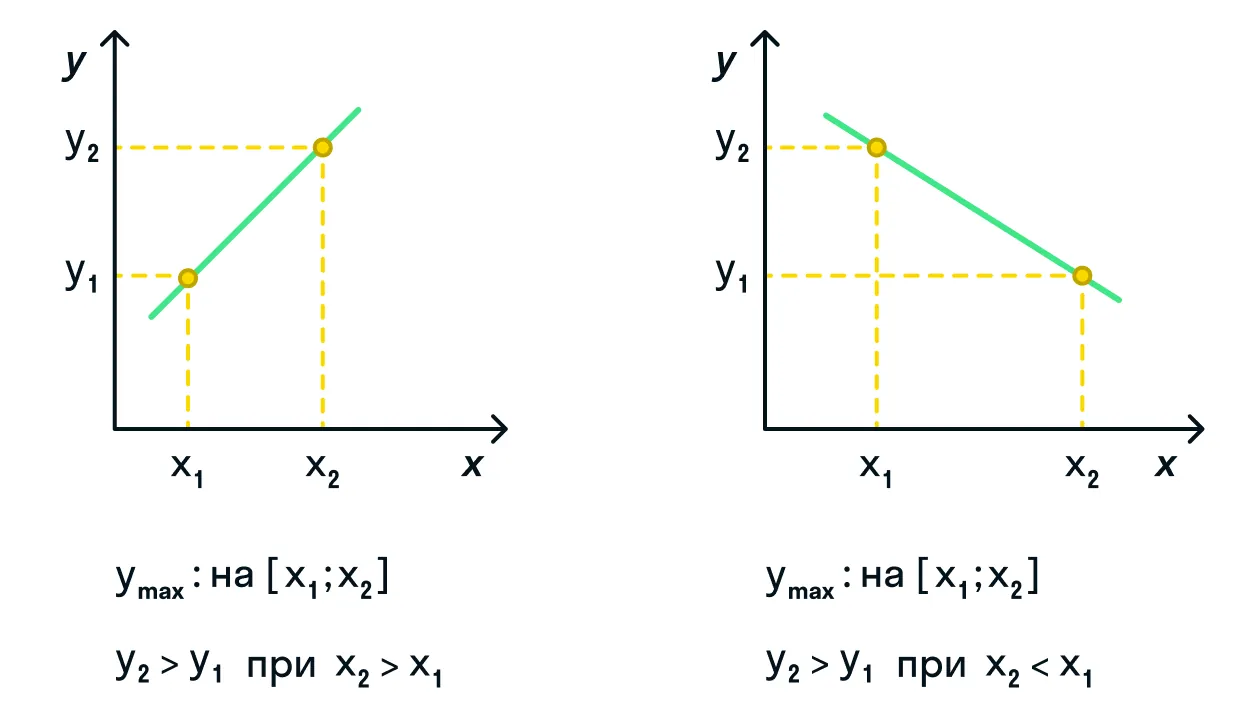
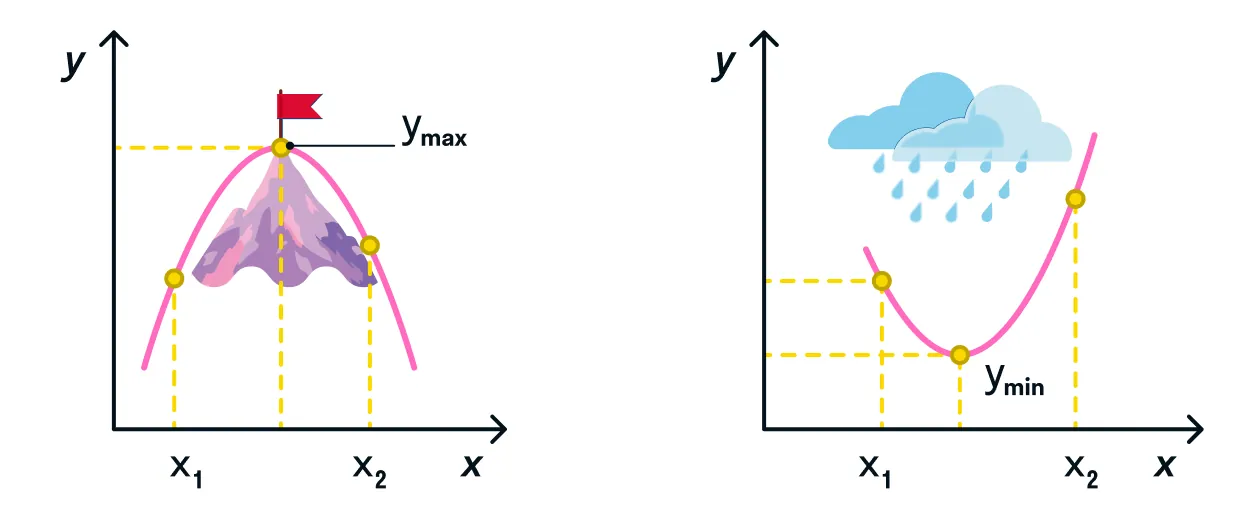
Если заданный интервал представлен кривой:

• максимальное значение функции выглядит как вершина горы, возвышенности, тогда как минимальное значение мы можем определить как самую низкую точку относительно этого пика;

• минимальное значение функции выглядит как дно низины, оврага, тогда как максимальное значение мы можем определить как самую высокую точку относительно этого пика.

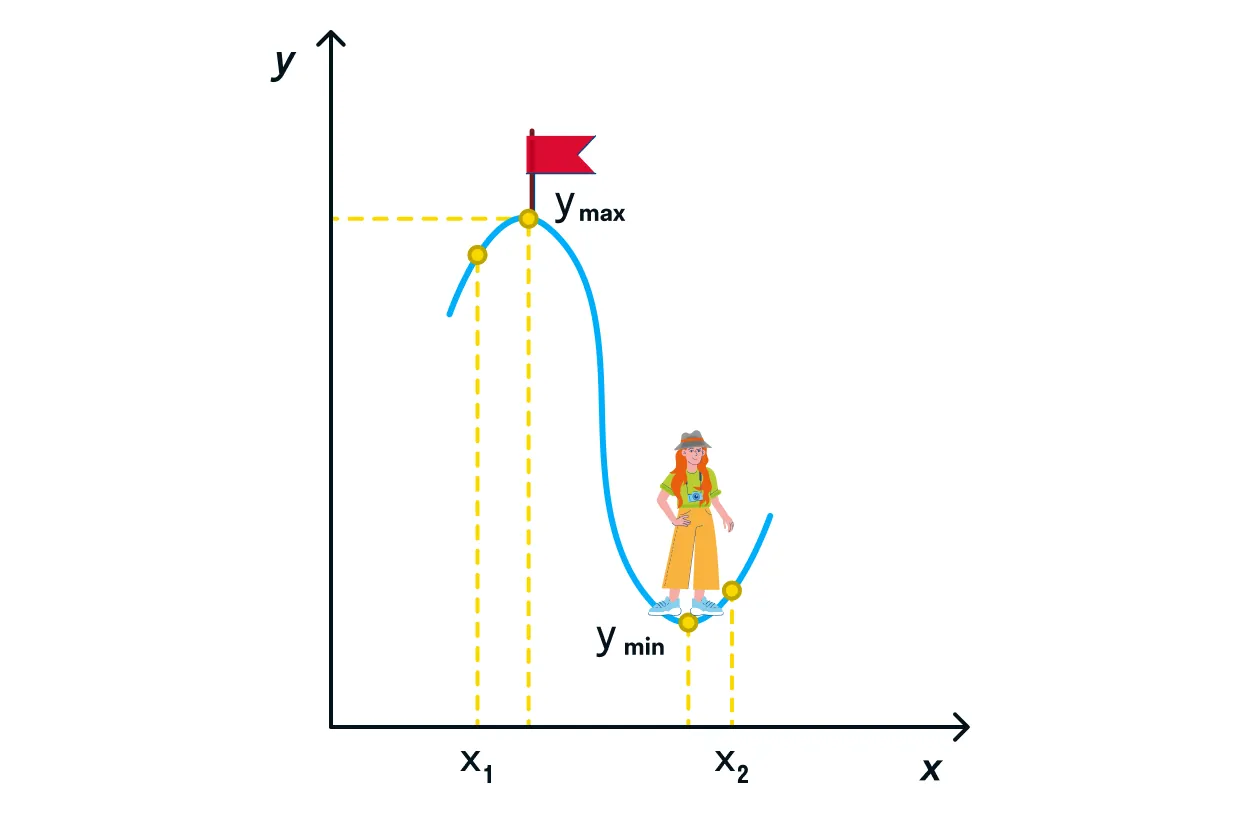
Возможен и такой вариант, когда горы и овраги встречаются на одном промежутке — тогда мы просто объединяем оба пункта для нахождения и Помним главное правило: максимальное значение функции всегда представлено самой высокой точкой относительно оси минимальное значение функции — самой низкой точкой.

Определение наименьшего и наибольшего значения через производную

Удобен ли способ нахождения и через график? Определённо! Всегда ли его можно использовать? К сожалению, нет.

Дело в том, что большинство заданий в алгебре на эту тему даются не через график, а через уравнение функции. Зачастую эти функции сложные, и построение их графиков займёт время. Ошибётесь в построении — допустите ошибку и в нахождении максимального и минимального значения, а нам это не нужно.

Способ, который не уступает первому в простоте и лаконичности, заключается в определении производной функции и поиске стационарных точек. Кажется, нам встретились два новых термина — давайте их разберём.

Производная функции — это отношение приращения функции к приращению аргумента при бесконечно малом приращении аргумента.

Производная функции показывает, как быстро увеличивается функция при бесконечно малом увеличении

По сути, найти производную означает провести определённые действия с помощью таблицы производных функций. Обязательно загляните в нашу статью об этом и изучите материал, а мы пока пойдём дальше.

Стационарная точка — точка, в которой значение аргумента производной функции равно нулю.

Дело в том, что по теореме Ферма в стационарных точках определяется экстремум функции, поэтому можно сделать вывод, что на некотором промежутке в них можно определить и наибольшее/наименьшее значение функции.

Алгоритм нахождения наибольшего и наименьшего значения непрерывной функции на отрезке

Как определить наибольшее и наименьшее значения функции на отрезке?

1. Найдём область определения данной функции и проверим, входит ли в неё заданный отрезок.

2. Найдём производную данной функции.

3. Приравняем производную к нулю и найдём точки, в которых она обращается в нуль (решим уравнение).

4. Выберем из корней уравнения те точки, которые попадают в заданный промежуток, и вычислим значение функции в них.

5. Возьмём точки начала и конца отрезка и найдём значение функции в них.

6. Сделаем вывод о наибольшем и наименьшем значении функции.

Разберём пару примеров.

Задача 1

Найдите наибольшее и наименьшее значение функции на отрезке

Решение:

1. ОДЗ:

4. не попадает в промежуток Найдём значение функции только в крайних точках:

5. Тогда является наименьшим значением на данном отрезке, а наибольшим.

Задача 2

Найдите наибольшее и наименьшее значение функции на отрезке

Решение:

1. ОДЗ:

3. , но в таком случае знаменатель равен нулю, что невозможно. А значит, производная не обращается в нуль, стационарных точек нет.

4. Найдём значение функции в крайних точках отрезка:

   — точка максимума на промежутке;

   — точка минимума на промежутке.

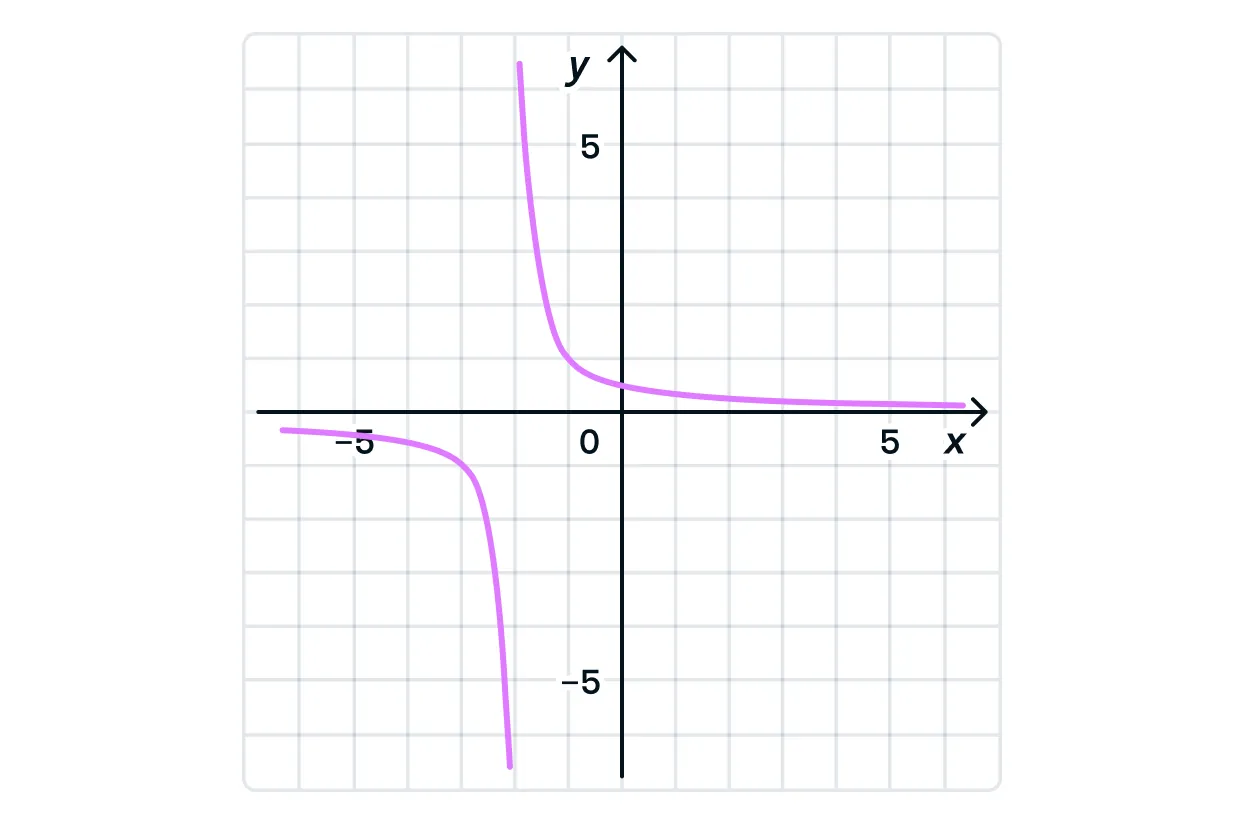
Наименьшее и наибольшее значение функции на открытом или бесконечном интервале

В чём отличие отрезка от интервала? В отрезке определены крайние точки, в интервале же крайние точки могут не существовать (например ), или значение функции в них мы рассматривать не будем (на интервале мы рассмотрим значение функции в окрестностях этих точек, но не в них самих).

Вариантов задания интервала может быть множество, но каждый из них сведёт определение и к поиску производной и вычислению пределов в крайних точках, например и

Вернёмся на пару шагов назад. А что такое предел функции?

Если говорить коротко, то предел функции — это такое число , к которому функция стремится, в то время как аргумент стремится достичь числа

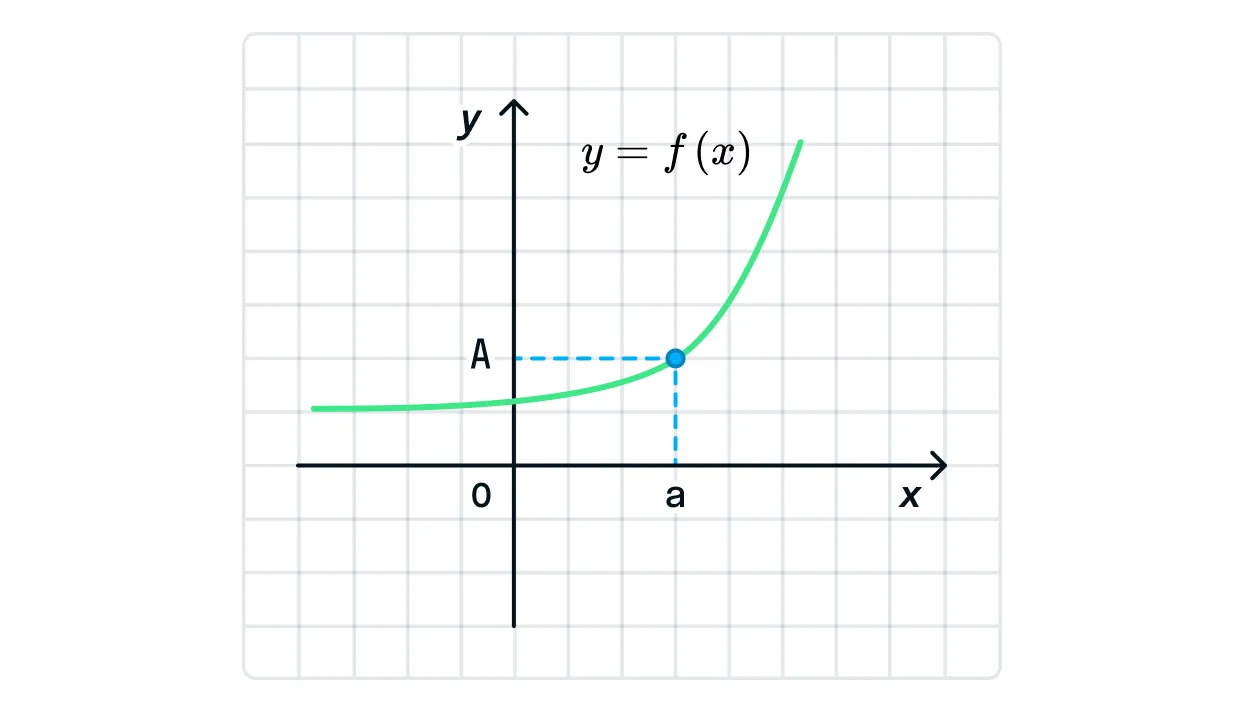
Предположим, наша функция представлена уравнением Найдём предел функции при подставив это значение вместо в уравнение:

Это означает, что функция стремится приблизиться к числу в то время как аргумент тоже приближается к этому значению. В отрыве от настоящего уравнения мы могли бы представить это так:

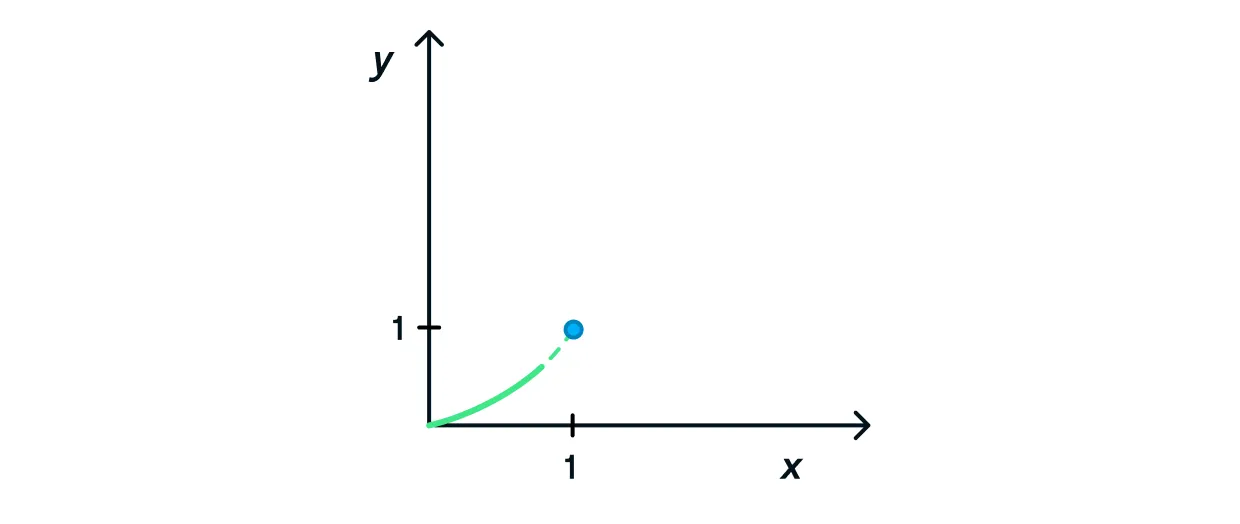
Функция может стремиться не только к рациональному числу, но также и к бесконечности. В таком случае при подстановке бесконечности в функцию возникает неопределённость, которую необходимо решить разными методами.

В рамках этой статьи мы не можем посвятить этому много времени, поэтому ждём Вас на курсах математики в онлайн-школе Skysmart — там ни один предел не останется незамеченным. 😉

Вернёмся к функции! Итак, как же определить наибольшее и наименьшее значение на интервале?

1. Найдём область определения данной функции и проверим, входит ли в неё заданный интервал.

2. Найдём производную данной функции.

3. Приравняем производную к нулю и найдём точки, в которых она обращается в нуль (решим уравнение).

4. Выберем из корней уравнения те точки, которые попадают в заданный промежуток, и вычислим значение функции в них.

5. Возьмём крайние точки интервала и вычислим значение предела в этих точках (согласно типу интервала).

6. Сделаем вывод о наибольшем и наименьшем значении функции.

Для вычисления предела вам поможет сводная таблица, которая учитывает вид интервала:

Интервал	Предел
	и
	и
	и

Если при вычислении одностороннего предела вы получаете бесконечность, то вычислить наибольшее/наименьшее значение невозможно.

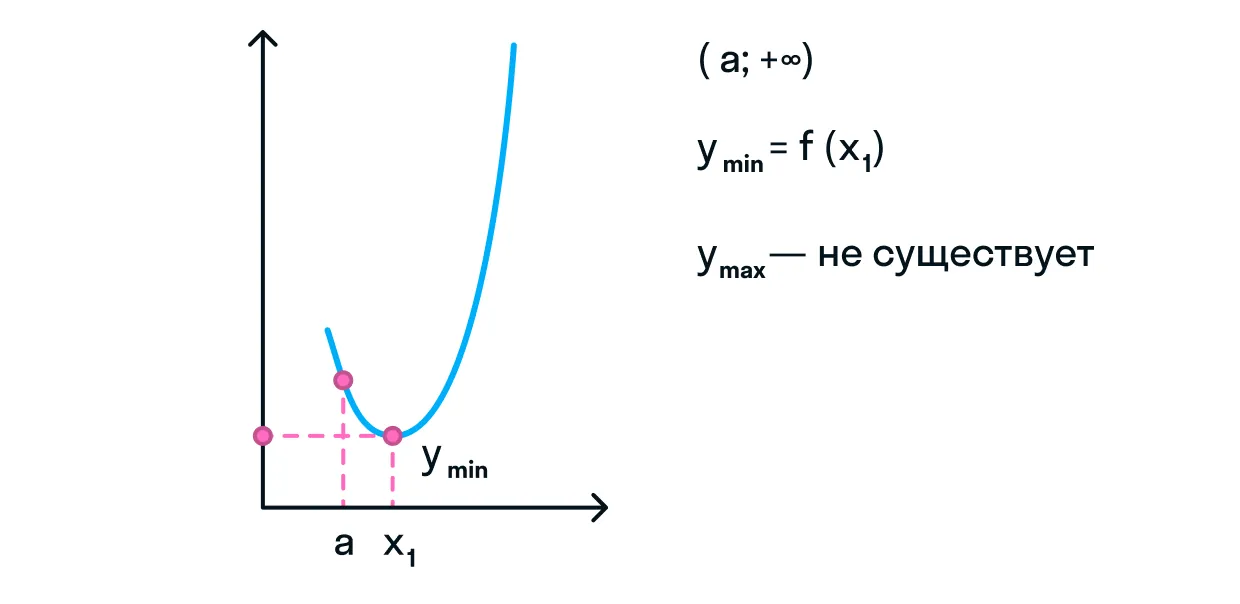
Задача 3

Необходимо найти наибольшее и наименьшее значение функции на всём промежутке области определения.

Решение:

1. ОДЗ:

3. Найдём стационарные точки:

4. Точка входит в промежуток области определения и является точкой минимума.

5. Так как — парабола, ветви которой направлены вверх, мы не можем определить точку максимума.

Cегодня мы на славу потрудились и разобрали множество важных вопросов:

• что такое функция, какой она бывает;

• что такое наименьшее и наибольшее значение функции;

• как определить и на отрезке;

• как находить наименьшее и наибольшее значение функции на интервале;

• что такое предел и производная.

Вот и ещё одна тема по математике стала понятнее! А если всё же остались вопросы, спешим ещё раз пригласить вас на уроки математики в Skysmart — мы постараемся ответить на них, закрепить материал и попрактиковаться в решении задач. Обещаем, будет увлекательно и безумно интересно!