Преобразование выражений

Зачем это нужно?

На самом деле, это отличный вопрос! В математике нет действий (по крайней мере, не должно быть), которые мы выполняем ради красоты записи или потому что хотим сделать решение более длинным, замысловатым или сложным.

Каждое преобразование должно соответствовать конкретной цели. При решении задач нам, как правило, хочется упростить их, сделать более лёгкими и понятными. А для этого мы хотим привести их к знакомому для нас виду, к алгоритму, который мы уже применяли. Именно поэтому так важно уметь пользоваться преобразованиями и применять их в нужный момент.

Основные тождественные преобразования

Давайте рассмотрим основные виды тождественных преобразований — ими пользуются чаще всего.

Перестановка местами слагаемых, множителей

От перестановки мест слагаемых или множителей значение выражения не меняется.

Это правило чаще всего применяется для более рационального (удобного) вычисления примеров.

В выражении 13 + 24 + 17 удобнее всего переставить слагаемые таким образом: 13 + 17 + 24 = (13 + 17) + 24 = 30 + 24 = 54. Но если мы оставим всё в первоначальном виде, всё равно придём к аналогичному ответу: 13 + 24 + 17 = (13 + 24) + 17 = 37 + 17 = 54.

Аналогично в выражении 5 ⋅ 99 ⋅ 2 лучше переставить множители так: 5 ⋅ 99 ⋅ 2 = 5 ⋅ 2 ⋅ 99 = 10 ⋅ 99 = 990.

Не обязательно записывать перестановку слагаемых или множителей подробно. Это можно сделать устно, но важно проговорить про себя причину, по который вы делаете это преобразование — таким образом поиск оптимального решения войдёт в привычку.

Раскрытие скобок

Раскрытие скобок применяется буквально везде: от решения уравнений и задач до работы с функциями.

Раскрытие скобок бывает трёх видов: при умножении одночлена на скобку, при умножении скобки на скобку и для выполнения суммы/разности.

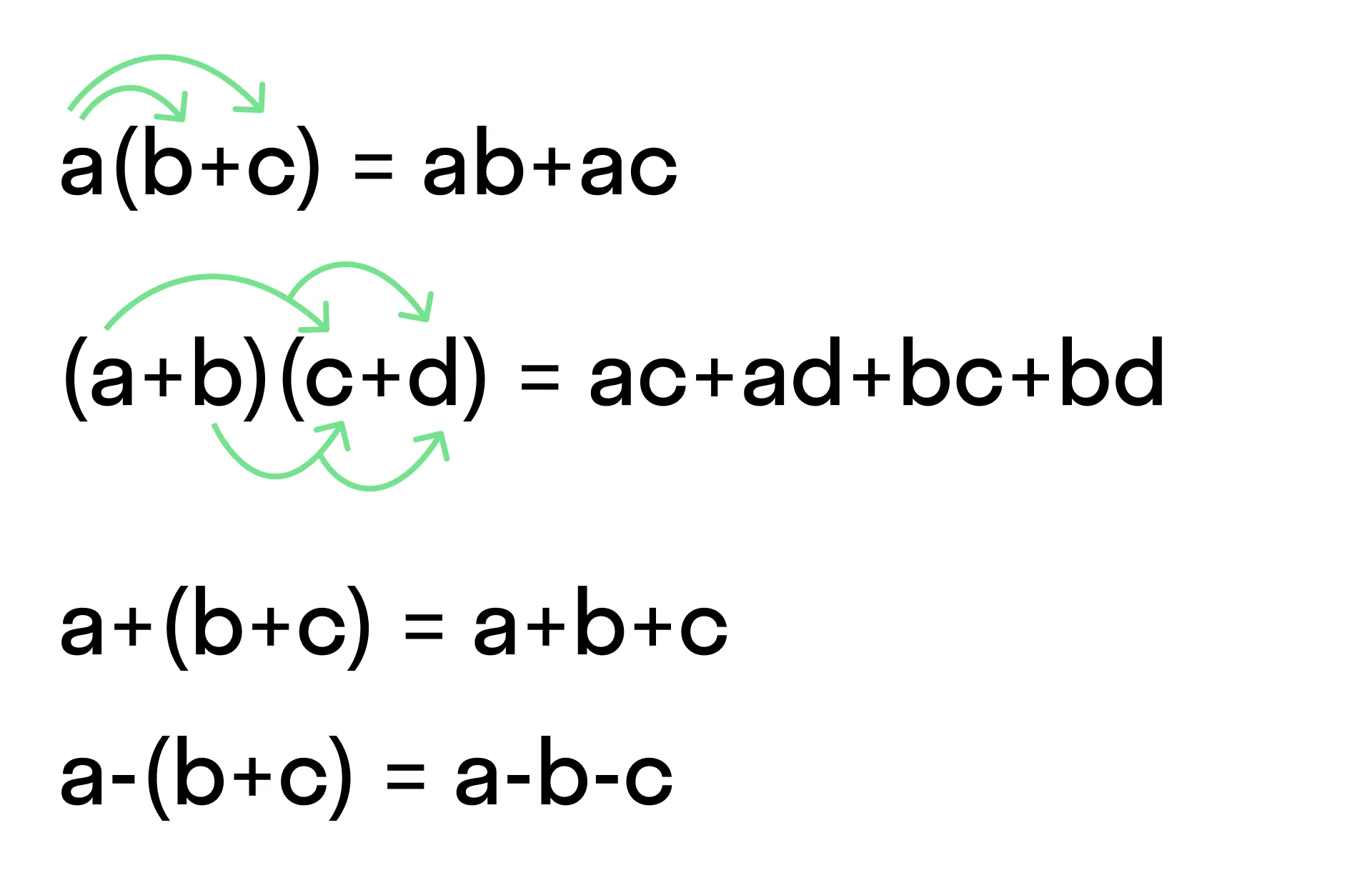
1. При умножении одночлена на скобку одночлен умножается на все слагаемые скобки, а между результатами умножение ставится знак, стоящий в скобке.

   Например: 2 (x − y) = 2x − 2y.

2. При умножении скобки на скобку каждое слагаемое первой скобки умножается на каждое слагаемое второй скобки, знаки ставятся согласно результату умножения.

   Например: (с + d) (x − y) = cx − cy + dx − dy.

3. При раскрытии скобок во время сложения или вычитания необходимо учитывать знак, стоящий перед скобкой:

   • если стоит знак плюс, скобки убираются, знак не влияет на содержимое: 1 + (20 − 6) = 1 + 20 − 6,

   • если стоит знак минус, скобки убираются, знаки одночленов в скобке меняются на противоположные: x − (2y + b) = x − 2y − b.

     Представьте, что вместо минуса перед скобкой стоит умножение на (−1), и, чтобы продолжить действия, вначале вам нужно найти значение этого произведения: x − (2y + b) = x + (−1) (2y + b) = x + (−2y) + (−b) = x − 2y − b.

Вынесение за скобки общего множителя

Вынесение общего множителя за скобки можно считать действием, обратным раскрытию скобок. Чаще всего это правило применяется для решения уравнений и неравенств.

128K

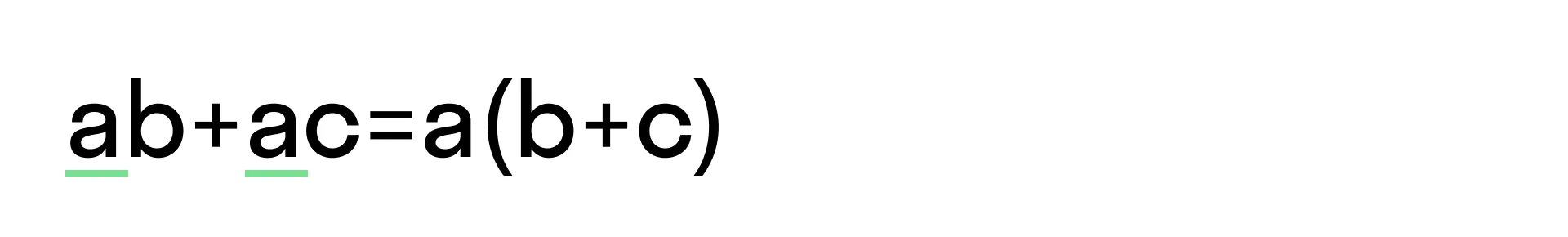
Вынесение общего множителя за скобкиЧитать →

Общий множитель может состоять из общей числовой и буквенной частей. Если общий множитель не виден сразу, необходимо разложить одночлен на произведение множителей.

Например, вынесем общий множитель в выражении 24xy² + 16x²y.

1. Разложим буквенные части на произведения простых множителей:

   24 = 4 ⋅ 6 = 2 ⋅ 2 ⋅ 2 ⋅ 3

   16 = 4 ⋅ 4 = 2 ⋅ 2 ⋅ 2 ⋅ 2

2. Представим степень буквенной части в виде произведения:

   xy² = x ⋅ y ⋅ y

   x²y = x ⋅ x ⋅ y

3. Запишем всё в виде произведения и подчеркнём множители, которые повторились в первом и втором выражениях:

   24xy² + 16x²y = 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ x ⋅ y ⋅ y + 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ x ⋅ x ⋅ y

4. Вынесем общие множители за скобки, а остальные поместим внутрь скобки, знак между выражениями оставим прежним:

   24xy² + 16x²y = 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ x ⋅ y ⋅ y + 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ x ⋅ x ⋅ y = 2 ⋅ 2 ⋅ 2 ⋅ x ⋅ y (3y + 2x) = 8xy (3y + 2x)

Рассмотрим ещё один пример. Решим уравнение:

x³ + x² = 0

Вынесем общий множитель за скобки:

x² (x + 1) = 0

Так как произведение равно нулю, один из множителей (или они оба) также равны нулю. Поэтому данное уравнение можно расписать на два других, приравняв множители к нулю. Получаем:

Так умение выносить общий множитель за скобки позволило нам решить уравнение быстрее и легче.

Группировка слагаемых или множителей

Под группировкой слагаемых или множителей подразумевается их перестановка и объединение в группы для более рациональных вычислений.

Например, выражение 2 + 17 + 25 + 18 + 33 мы преобразуем таким образом:

2 + 17 + 25 + 18 + 33 = (2 + 18) + (17 + 33) + 25 = 20 + 50 + 25 = 95.

Метод группировки чаще всего используется в тандеме с другими методами. Так, если мы хотим вынести общий множитель в большой группе слагаемых, мы разобьём сумму на подгруппы и выполним вынесение:

x³ + 2x² + x + 2 = (x³ + x) + (2x² + 2) = x (x² + 1) + 2(x² + 1) = (x² + 1) (x + 2)

Обратите внимание:

1. В данном выражении можно по-разному группировать слагаемые. Мы могли бы сделать так:

   x³ + 2x² + x + 2 = (x³ + 2x²) + (x + 2) = x² (x + 2) + (x + 2) = (x² + 1) (x + 2)

2. Общим множителем может выступать целая скобка.

Замена разностей суммами, частных произведениями и наоборот

В математике действия сложения и вычитания, умножения и деления можно назвать обратными друг другу, и часто они взаимозаменяемы.

Замену разности суммой и наоборот легко продемонстрировать на действиях с числами разных знаков:

−2 − 5 = −2 + (−5) = −7

16 − 20 = 16 + (−20) = −8

−9 + 11 = 11 + (−9) = 11 − 9 = 2

Действия умножения и деления также могут заменять друг друга:

20 : 5 = 20 ⋅ 1/5 = 4

x : y = x ⋅ 1/y

16 ⋅ 0,1 = 16 ⋅ 1/10 = 16 : 10 = 1,6

Выполнение действий с числами

При решении арифметических примеров или уравнений мы можем выполнить небольшие промежуточные действия: например, извлечь квадратный корень, возвести число в степень, выполнить сложение или вычитание чисел, сократить дроби.

Например, данное уравнение лучше преобразовать таким образом:

√4x² + 3²x − 12/15 = 0

2x² + 9x − 0,8 = 0

Но не всегда нужно выполнять сразу промежуточные действия с числами: порой более просто и рационально будет воспользоваться другим методом.

Например, в выражении 101² − 99² намного быстрее будет воспользоваться формулами сокращённого умножения, а не возводить в степень и вычитать:

101² − 99² = (101 + 99) (101 − 99) = 200 ⋅ 2 = 400

Сравните с такими вычислениями (при учёте что вы считаете всё без калькулятора):

Приведение подобных слагаемых

Приведение подобных слагаемых — ещё один навык, без которого не решить большинство заданий с уравнениями и неравенствами.

Подобные слагаемые — одночлены, буквенная часть которых полностью совпадает (с учётом степеней).

12.3K

Подобные слагаемые и их приведениеЧитать →

Выражения 16ab и 24ab — подобные слагаемые, их можно складывать и вычитать, т. е. мы складываем (вычитаем) их числовые коэффициенты, при этом буквенные части остаются прежними:

16ab + 24ab = (16 + 24) ab = 40ab

16ab − 24ab = (16 − 24) ab = −8ab

Выражения 10x² и 10x подобными не являются, так как степени их буквенной части различаются, хотя и там, и там использовали x.

Подобные слагаемые чаще всего образуются при раскрытии скобок:

(x + 1) (x + 2) = x² + 2x + x + 2 = x² + 3x + 2

Прибавление и вычитание одного и того же числа

К одному выражению мы можем прибавить число и тут же вычесть его. Для чего это делают? Такой метод используется в разных случаях, в том числе для выделения целого квадрата выражения.

x² + 6x = x² + 6x + 9 − 9 = (x² + 6x + 9) − 9 = (x + 3)² − 9

Похожий метод применяется для решения уравнений, когда мы можем прибавить или вычесть число сразу из двух частей:

x − 2 = 0

x − 2 + 2 = 0 + 2

x = 2

Обе части уравнения можно также умножить и разделить на одно и то же число, отличное от нуля.

1/3 x² + 2/3 x + 6 = 0 | ⋅ 3

3 (1/3 x² + 2/3 x + 6) = 0 ⋅ 3

x² + 2x + 18 = 0

Замена чисел и выражений тождественно равными им выражениями

Ещё один метод преобразования выражений — замена их тождественно равными. Здесь хочется обратить особое внимание на формулы сокращённого умножения, которые используют для таких замен.

Эти формулы были не придуманы, а получены с помощью перечисленных выше преобразований.

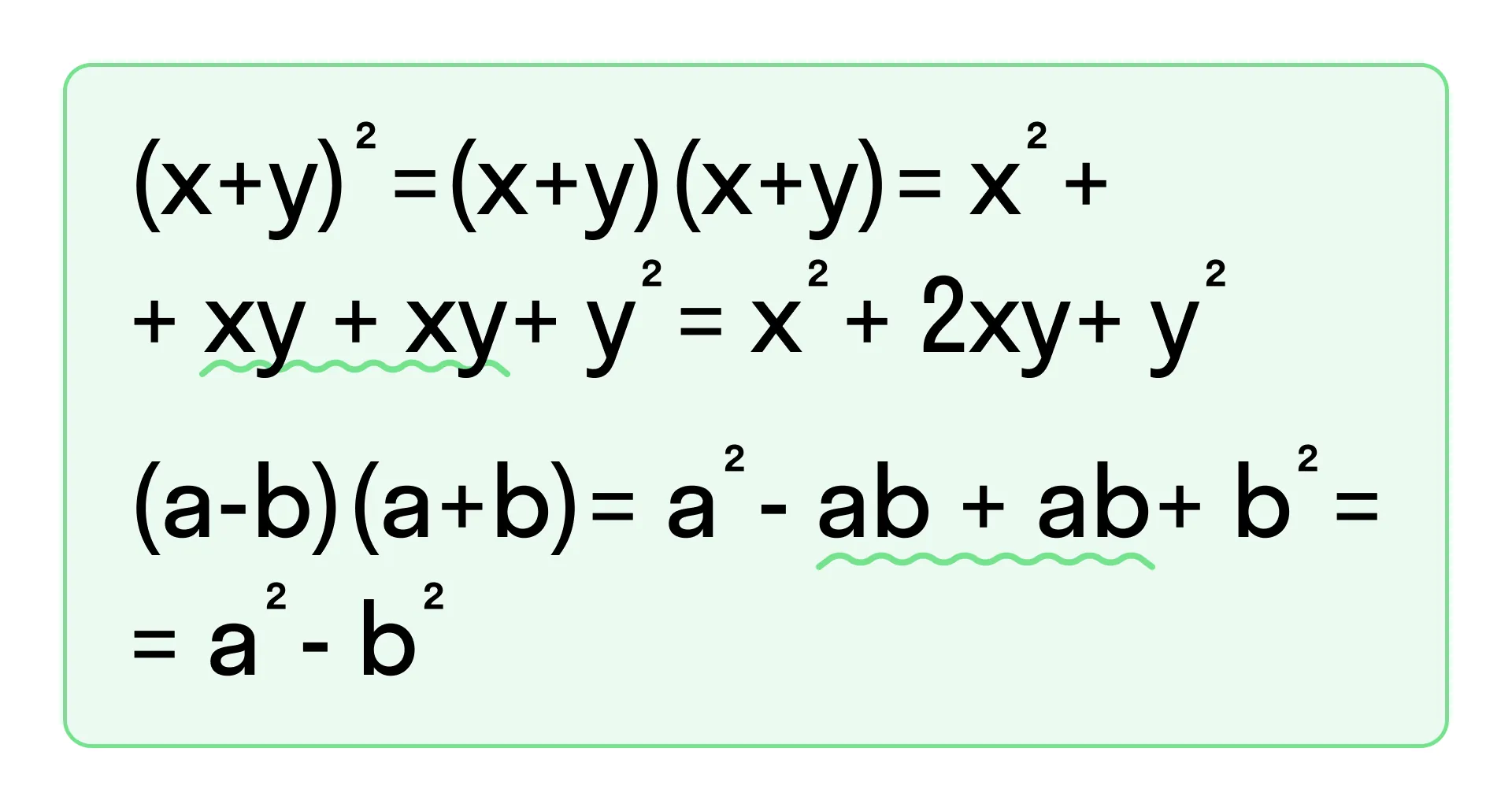
Их можно использовать сразу как готовое решение, не расписывая при этом подробно.

170.4K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Тождественные преобразования и ОДЗ

Для преобразования дробно-рациональных и иррациональных выражений обязательно нужно учитывать область допустимых значений. Это часто применяется для решения уравнений, исследования функций и пределов.

Например, если нам необходимо преобразовать выражение в рамках задания на сокращение дробей, мы можем легко это сделать: .

Если же мы решаем уравнение , в таком случае знаменатель дроби не может быть равен нулю (так как на ноль делить нельзя), и нам нужно учесть ОДЗ: .

В исследовании функции мы можем сократить равные скобки только после того, как пропишем ОДЗ: , и при построении графика точка с координатой будет выколотая.

Понимание, какой метод использовать лучше, как быстрее прийти к верному ответу, и что именно здесь лучше преобразовать, приходит с практикой. Приглашаем закрепить знания в бесплатном тренажёре ЕГЭ, который подготовит вас к любым контрольным и экзаменам!