Вынесение общего множителя за скобки

Для кого эта статья:

• Ученики начальных и средних классов, изучающие математику
• Учителя и репетиторы, ищущие материалы для объяснения понятия общего множителя
• Родители, которые помогают детям с домашними заданиями по математике

Что такое общий множитель

Начнем с самого простого: что такое множитель?

Множитель — число, показывающее, сколько раз повторяется слагаемым другое число для получения произведения.

Иначе говоря, множитель — это число, которое участвует в процессе умножения.

• В примере множителями являются числа 2 и 3, а 6 — значение произведения или результат умножения.

• В примере множителями являются числа 2 и 15, а 30 — значение произведения или результат умножения.

Понятие «множитель» можно встретить и при решении уравнений. Так, в уравнении между числом 2 и буквой х опущен знак умножения, а значит, 2 — это известный множитель, а х — неизвестный.

Могут ли множители быть общими? Вполне! Предлагаем разложить на простые множители два числа и сравнить получившиеся ряды чисел: может, какие-то из множителей повторятся?

Возьмем числа 36 и 15:

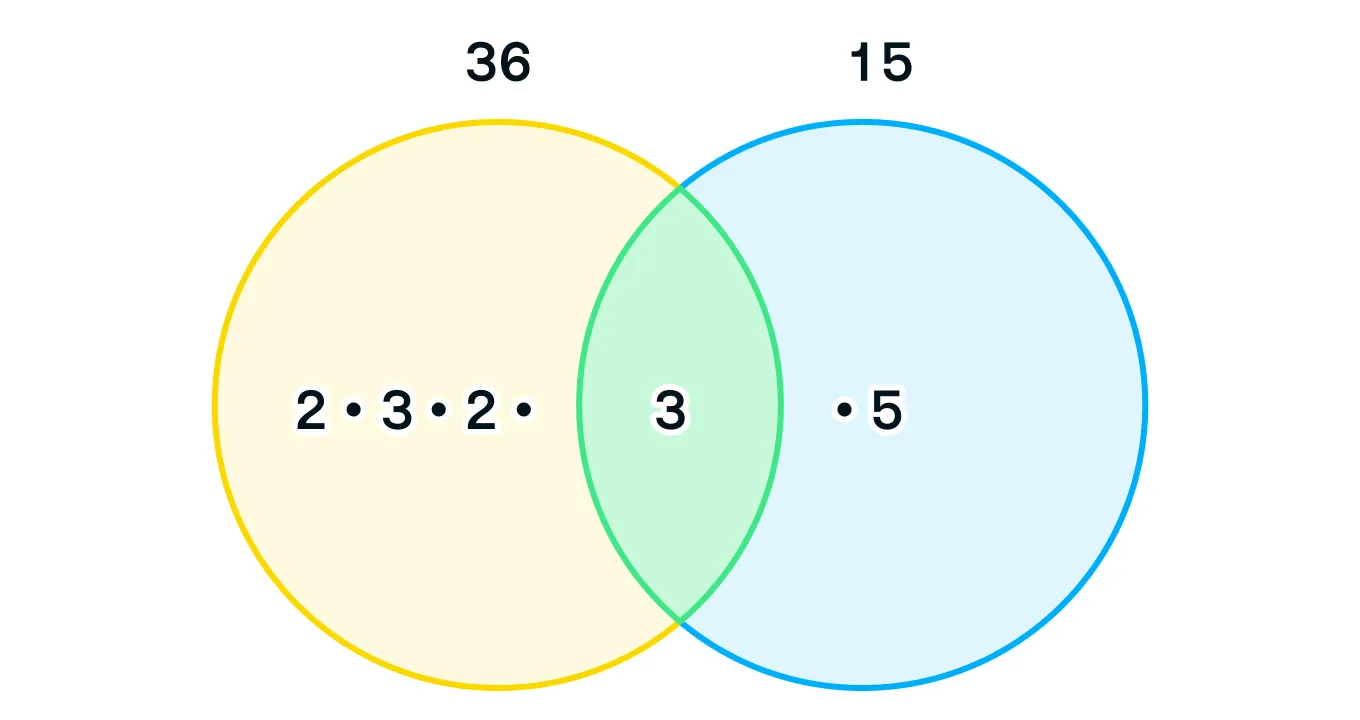
Как мы видим, общий множитель для чисел 36 и 15 (т. е. множитель, который присутствует в разложении обоих чисел) — это число 3.

Распределительный закон

Еще лучше понять природу общего множителя помогает распределительный закон умножения, который изучают в 5-м классе.

Повторим его формулировку:

Чтобы сумму чисел умножить на число, нужно каждое слагаемое отдельно умножить на число и полученные произведения сложить.

Кстати, то же самое правило работает и для разности: чтобы разность чисел умножить на число, нужно умножить на число уменьшаемое и вычитаемое и из первого произведения вычесть второе.

Приведем примеры:

Особенно внимательные читатели заметили, что последний пример немного отличается от остальных: в нем число стоит не перед скобками, а после. Не переживайте, так можно и даже нужно! На алгоритм раскрытия скобок не влияет, где стоит число, а значит, мы можем сами выбрать, поставить его в начале или в конце примера.

Распределительный закон очень удобно иллюстрировать стрелочками:

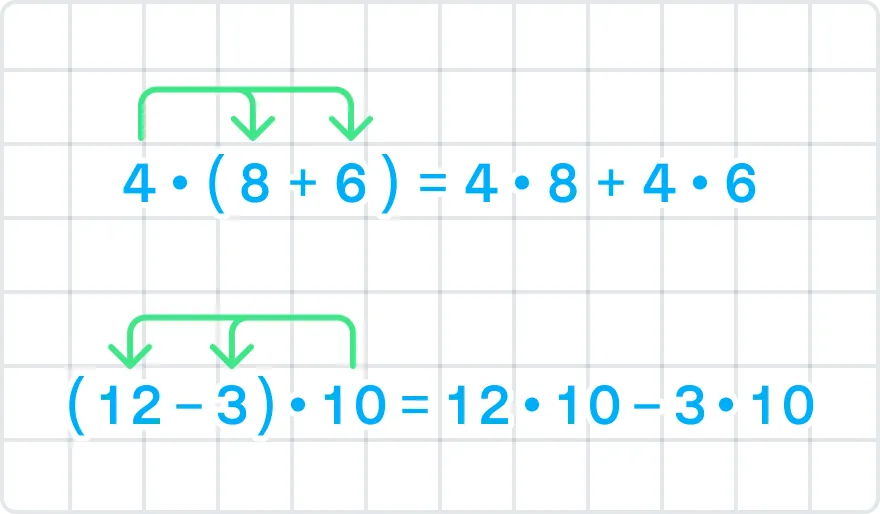
С ними сразу становится ясно, в каком порядке произвести действия!

Распределительный закон можно записать в общей форме, подставив вместо чисел буквы:

Можно сказать, что запись в таком виде является шаблоном или формулой. Мы должны запомнить, что вместо букв a, b, c мы можем подставить все что угодно: дроби, смешанные числа, другие буквы и даже целые примеры.

222.3K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Прокачивай знания на курсах математики

• Выбирай из 1200+ репетиторов по математике

• Записывайся на бесплатные курсы для детей

Обратная запись распределительного закона

«Постойте, но как это относится в общему множителю? По-моему, все только стало сложнее…»

Понимаем ваши чувства, но уверяем: сейчас мы во всем разберемся!

Дело в том, что мы можем немного переписать распределительный закон, поменяв части местами:

если

то и

А это уже стандартное вынесение общего множителя за скобки! Можно сказать, что это действие является обратным умножению скобки на число. В нашей буквенной форме а — общий множитель, когда мы выносим его за скобки, получаем сумму . Таким образом мы получили формулу вынесения общего множителя за скобки.

Рассмотрим числовые примеры вынесения общего множителя за скобки:

Итак, что называют вынесением общего множителя за скобки? Это математическое действие, которое подразумевает преобразование выражения с помощью распределительного свойства умножения.

Алгоритм вынесения общего множителя за скобки

Примеры, которые мы рассмотрели выше, были довольно простыми: в них мы сразу видели, какое число является общим множителем для суммы или разности. Но что если в исходном задании общий множитель не будет явным?

Например: вынесите общий множитель за скобки в выражении .

В этом примере не только появились буквы, но еще и числа 20 и 4 не разложены на множители.

Чтобы успешно выполнить вычисления, воспользуемся правилом вынесения общего множителя за скобки:

1. Найдем НОД числовых коэффициентов.

2. Проанализируем буквенные части одночленов (если выражение представляет собой многочлен).

3. Поделим каждый одночлен на НОД и общие буквы в наименьших степенях.

4. Вынесем общий множитель за скобки, внутрь скобок поместим результаты деления и исходный знак (если была сумма — то плюс, если разность — минус).

Самое лучшее, что мы можем сделать сейчас, — закрепить использование этого алгоритма на практике. Этим и займемся!

Примеры вынесения общего множителя за скобки

Задание 1

Вынесите общий множитель за скобки в выражении .

Решение.

Для того чтобы вынести общий множитель за скобки, найдем наибольший общий делитель для двух чисел.

Чтобы найти НОД, нужно разложить эти числа на простые множители, а затем найти произведение общих множителей.

Чтобы разложить число на простые множители, будем делить число на ряд натуральных чисел от 2 и далее и так повторим с каждым результатом деления.

Обратите внимание на запись: 24 делится на 2 (начинаем именно с двойки), под числом 24 мы записываем результат деления и так далее. 3 не делится на 2, зато делится на 3, в результате мы получаем 1 и заканчиваем деление.

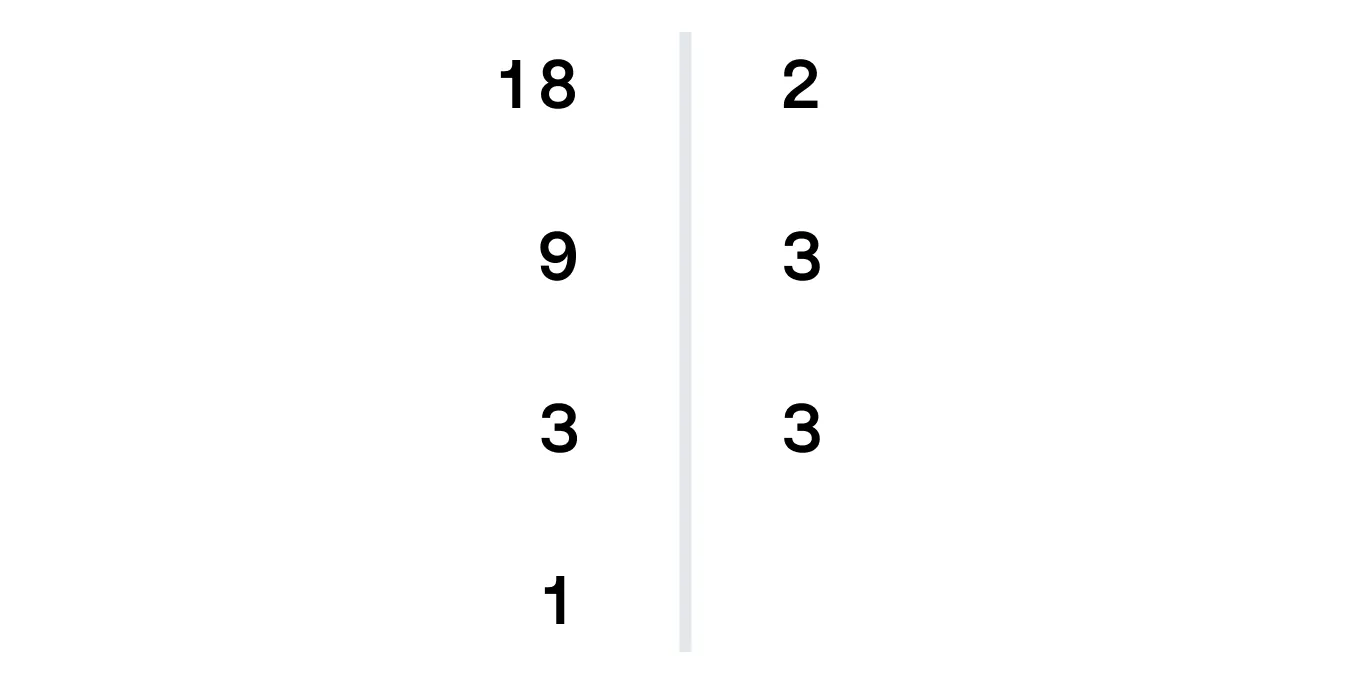
Сравним полученные ряды чисел:

Совпали числа 2 и 3.

Значит, НОД . Число 6 — это и есть общий множитель, его мы вынесем за скобки:

Задание 2

Вынесите общий множитель за скобки в выражении .

Решение:

1. Найдем НОД чисел 54 и 12.

2. Разделим оба числа на НОД.

3. Запишем результат, где перед скобками стоит НОД, а в скобках — сумма результатов деления.

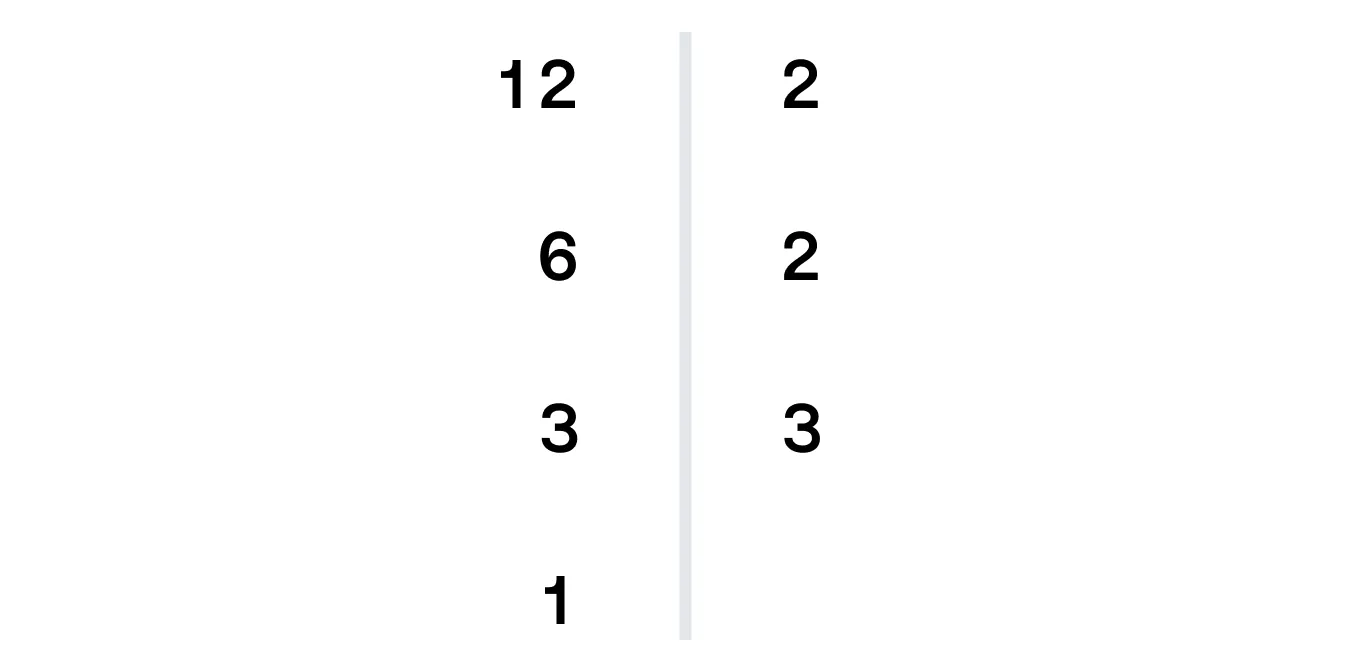
НОД

Задание 3

Произведите преобразования многочлена и вынесите общий множитель за скобки в выражении .

Решение:

1. Видим, что выражение представляет собой многочлен (сумму одночленов — выражений, содержащих произведение числового коэффициента и буквенной части).

   

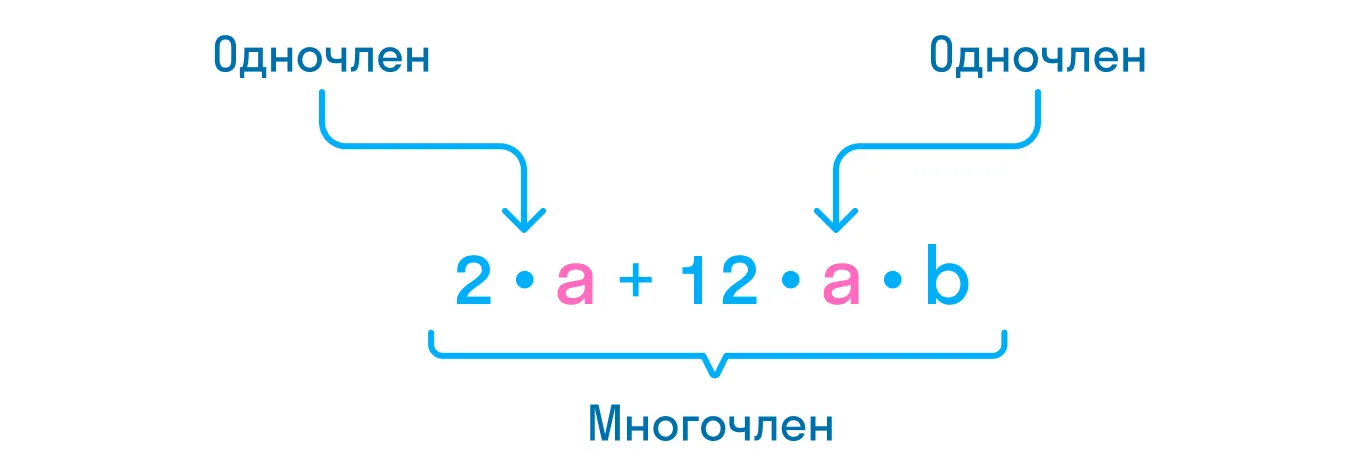
   В обоих одночленах буква а является общей, а значит, она будет входить в общий множитель.

2. Найдем НОД для чисел 2 и 12:

   НОД

3. Общим множителем, исходя из пунктов 1 и 2, будет являться выражение 2а.

Сделаем проверку, раскрыв скобки в полученном произведении:

Задание 4

Вынесите общий множитель за скобки в многочлене

Решение:

1. Видим, что выражение представляет собой многочлен (сумму одночленов — выражений, содержащих произведение числа и буквы). В одночленах 24xy и 15z нет общей буквы, все они разные, а значит, они не являются общими множителями.

2. Найдем НОД чисел 24 и 15:

   НОД

Сделаем проверку, раскрыв скобки в полученном произведении:

Задание 5

Вынесите общий множитель за скобки в выражении

1. Видим, что выражение представляет собой многочлен. Проанализировав одночлены, мы замечаем, что в каждом из них есть х, но в разных степенях. Как общий множитель мы возьмем х в наименьшей степени, т. е. x¹, или x.

   Обратите внимание: хотя у присутствует в двух из трех одночленов, этого недостаточно для вынесения его за скобки в качестве общего множителя.

2. Рассчитаем НОД: НОД (8, 16, 4) = 4.

3. В данном выражении дополнительно можно вынести знак минус (но это необязательно). Чтобы это учесть, в качестве общего множителя возьмем −4x.

Подведем итоги

• Вынесение общего множителя за скобки — это математическое действие, которое основано на распределительном законе умножения.

• Использование этого метода значительно упрощает вычисления.

• Метод вынесения общего множителя за скобки: необходимо найти НОД числовых коэффициентов и повторяющуюся букву в ее наименьшей степени и разделить на общий множитель все одночлены.

Чтобы еще лучше закрепить темы «Вынесение общего множителя за скобки» и «Разложение многочлена на множители», приглашаем на онлайн-уроки математики в школе Skysmart! Удобная платформа, курсы по подготовке к ВПР и экзаменам, а также поддержка опытных преподавателей — что может быть полезнее и увлекательнее?