Площадь треугольника — это величина, характеризующая размер его поверхности. Основная формула для нахождения площади треугольника звучит так: Площадь треугольника равна половине произведения длины основания и высоты, проведённой к этому основанию. S = (a * h) / 2.
Примеры:
- При основании a = 5 см и высоте h = 4 см, площадь S = (5 * 4) / 2 = 10 см².
- Если основание a = 8 м и высота h = 3 м, площадь S = (8 * 3) / 2 = 12 м².
Для кого эта статья:
- Студенты и ученики, подготовляющиеся к экзаменам по математике
- Преподаватели математики и репетиторы
- Все, кто интересуется основами геометрии и расчетом площади треугольника
Онлайн-калькулятор площади треугольника
Формула:
Основание:
Высота:
Результат:

Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Популярные единицы измерения площади:
квадратный миллиметр (мм2);
квадратный сантиметр (см2);
квадратный дециметр (дм2);
квадратный метр (м2);
квадратный километр (км2);
гектар (га).
Получи больше пользы от Skysmart:
-
Подготовься к ОГЭ на пятёрку
-
Подготовься к ЕГЭ на высокие баллы
Записывайся на бесплатные курсы для детей
Решай задания в бесплатном тренажёре ЕГЭ
Формула площади треугольника
Формула площади треугольника - это математическое выражение для вычисления площади треугольника. Одна из формул: S = (a * h) / 2, где a - основание, h - высота.
Пример: если a = 6 см, h = 4 см, то S = 6 * 4 / 2 = 12 см².
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Пройдите тест и узнайте, какие темы отделяют от пятёрки по математике
Добро пожаловать в школу магии.
О нет! Мальчик-молния случайно попал в школьные часы. Теперь они отстают. Мы все можем задержаться в школе
Жми на стрелки сверху, чтобы путешествовать в истории→
Одна ученица когда-то была в школьной кладовке и видела там схему часов
Но в кладовку просто так не попадёшь→
Реши два примера от волшебной статуи на входе в кладовку
Схема у нас!
Деталь можно сделать из проволоки и формы для заливки металла. Найди их на картинке
Теперь осталось взять инструменты у садовника! Он обменяет их на волшебные бобы для его сада
Для починки часов нужны: молоток, отвертка и плоскогубцы.
Ты можешь либо одолжить у садовника набор, либо отдельные инструменты, либо и то, и другое. Какое минимальное количество волшебных бобов ты можешь отдать садовнику?
Деталь имеет форму прямоугольника со сторонами 5 см и 12 см. Найди периметр и площадь детали, чтобы посчитать, сколько проволоки для неё понадобится
Периметр прямоугольника равен
Площадь прямоугольника равна
Мальчик-молния выплавил деталь, часы должны работать! Но они почему-то не идут... Кажется, одной шестерёнки не хватает — она куда-то упала
В коробке, шкатулке, ящике и банке находятся пыльца, волчий корень, золото и шестерёнка. Шестерёнка и пыльца не в коробке, ёмкость с волчьим корнем стоит между ящиком и ёмкостью с золотом, в банке не волчий корень и не шестерёнка. Шкатулка стоит около банки и ёмкостью с пыльцой. В какой ёмкости что находится?
Соедини ёмкости с содержимым на картинках ниже
Ура, мы вставили последнюю шестеренку, и часы пошли! Сегодня уроки закончатся вовремя. Спасибо тебе за помощь!
Дальше узнаешь свои результаты →
Формулы площади для любого треугольника
1. Площадь треугольника через основание и высоту
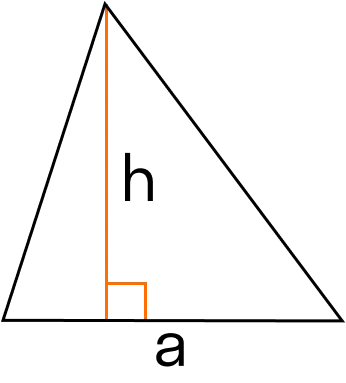
2. Площадь треугольника через две стороны и угол между ними.

3. Площадь треугольника через описанную окружность и стороны

4. Площадь треугольника через вписанную окружность и стороны.

5. Площадь треугольника по стороне и двум прилежащим углам
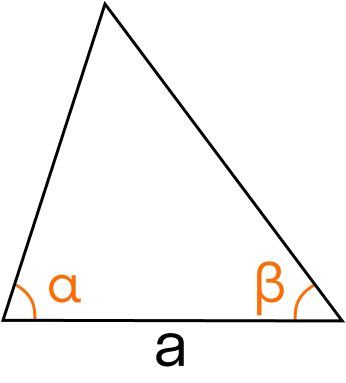
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
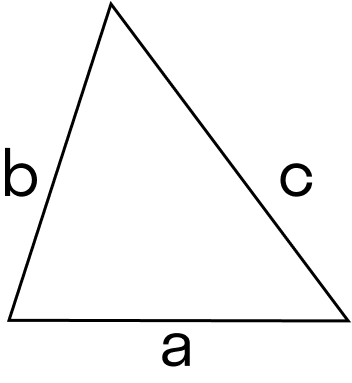
Для прямоугольного треугольника
Для прямоугольного треугольника чаще всего используют одну формулу — половину произведения катетов. Потому что их всегда можно найти с помощью правил тригонометрии или теоремы Пифагора.

Площадь треугольника по гипотенузе и острому углу
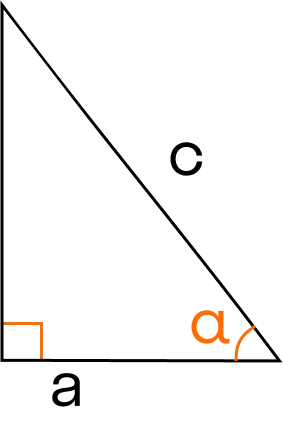
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
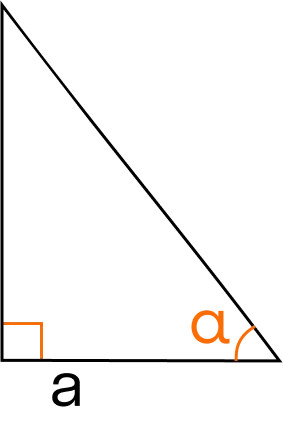
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и радиус вписанной окружности

Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
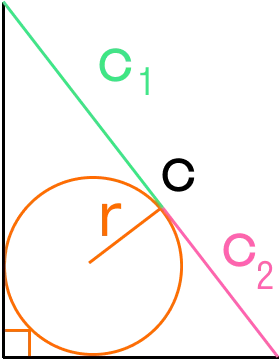
Площадь прямоугольного треугольника по формуле Герона

Для равнобедренного треугольника
Ниже мы покажем разные формулы для площади равнобедренного и равностороннего треугольника, их редко используют, но их легко вывести самому. Попробуйте сделать это самостоятельно.
Вычисление площади через основание и высоту
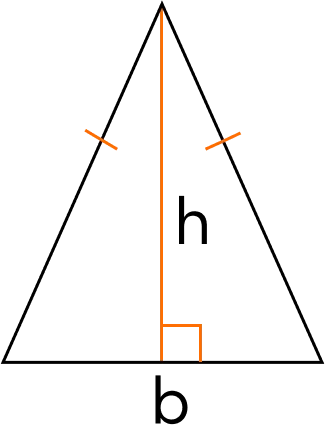
Поиск площади через боковые стороны и угол между ними.
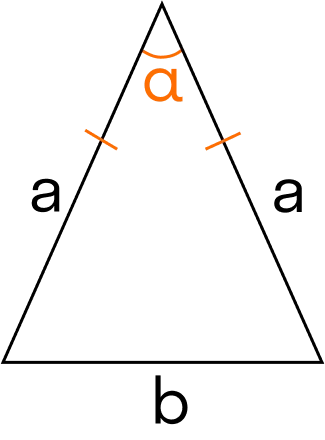
Площадь равностороннего треугольника через радиус описанной окружности

Площадь равностороннего треугольника через радиус вписанной окружности

Площадь равностороннего треугольника через сторону
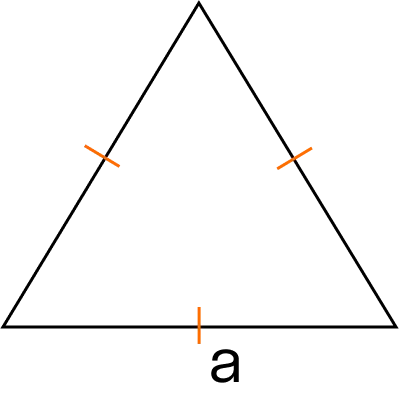
Площадь равностороннего треугольника через высоту
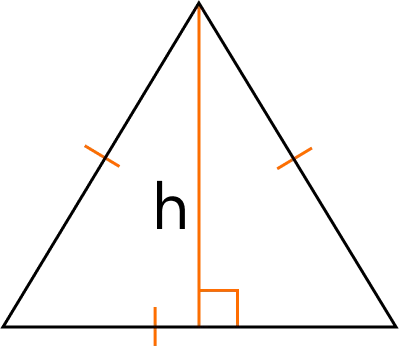
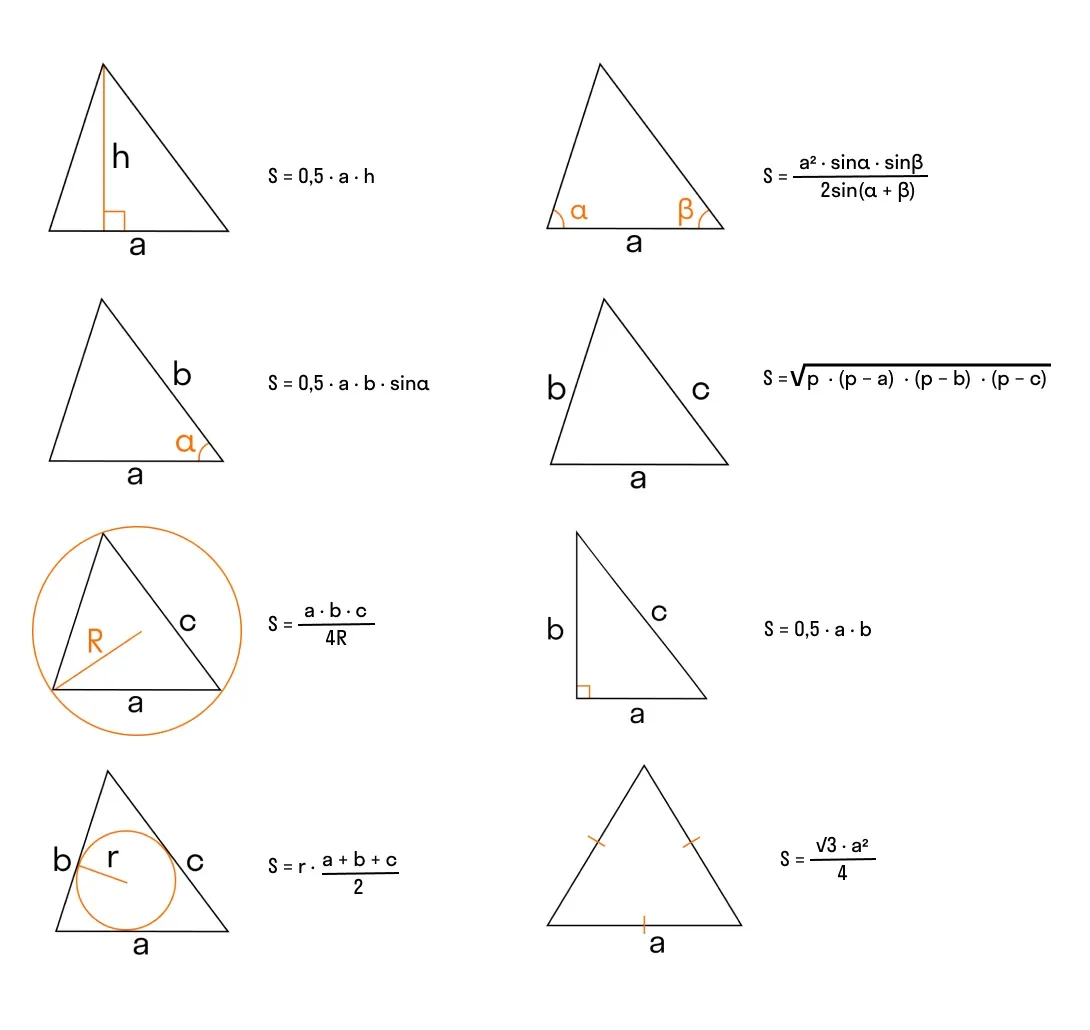
Таблица формул нахождения площади треугольника
В задачах встречаются разные фигуры, и кажется, что нужны разные формулы. Но на самом деле, зная всего несколько формул для треугольника и пользуясь теоремами и свойствами геометрии, можно найти площадь любой фигуры.
Но что делать, если нужно решить контрольную по математике или геометрии быстро, а вы плохо знаете конкретную тему? Закажите контрольную по математике онлайн у специалистов, которые помогут быстро выполнить задание и пояснят решение.






















