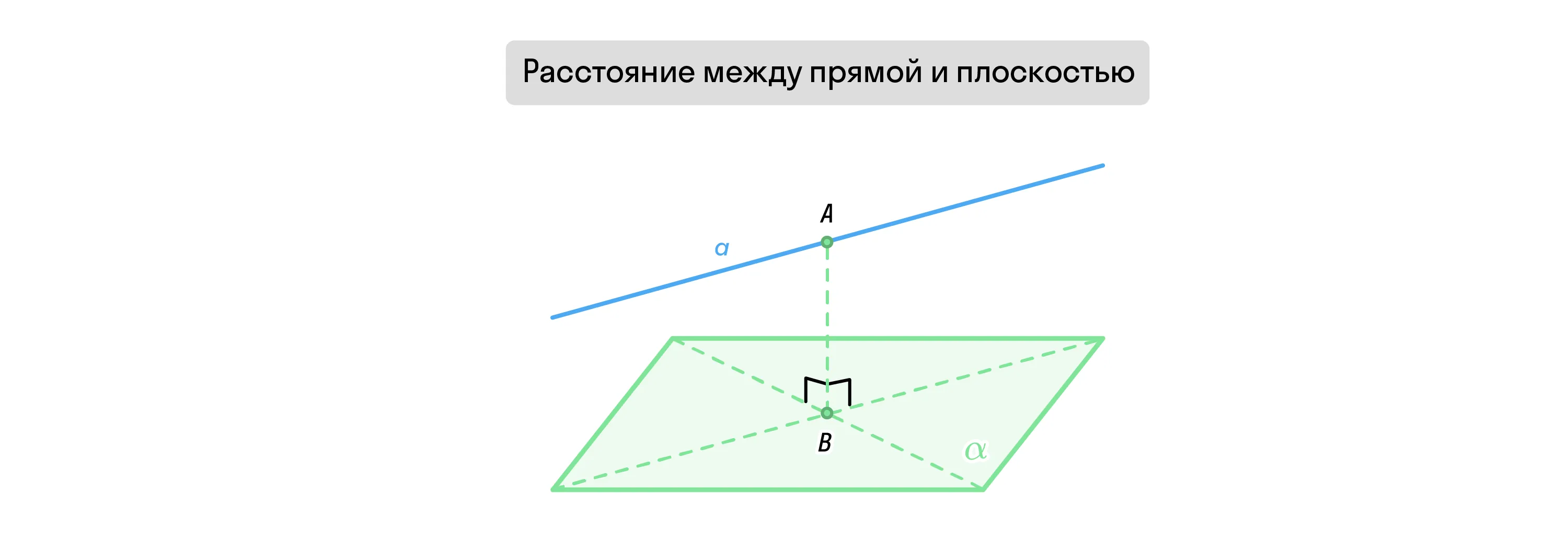
Расстояние между параллельными прямой и плоскостью — это расстояние, которое разделяет любую точку этой прямой и заданную плоскость.
Чтобы понять, как находить это расстояние, разберём пример. Для этого проложим прямую a и обозначим параллельную ей плоскость α. Далее отметим на прямой произвольную точку A и опустим от неё перпендикуляр к плоскости. Он пересечёт её в точке, которую обозначим как B. Длина отрезка AB — это и есть расстояние между прямой и плоскостью.
Теорема
Когда прямая a параллельна плоскости α, все точки прямой a равноудалены от этой плоскости.
Чтобы доказать эту теорему, снова построим прямую а и плоскость α. Далее отметим на прямой произвольную точку и проведём через неё плоскость α1, параллельную заданной ранее.
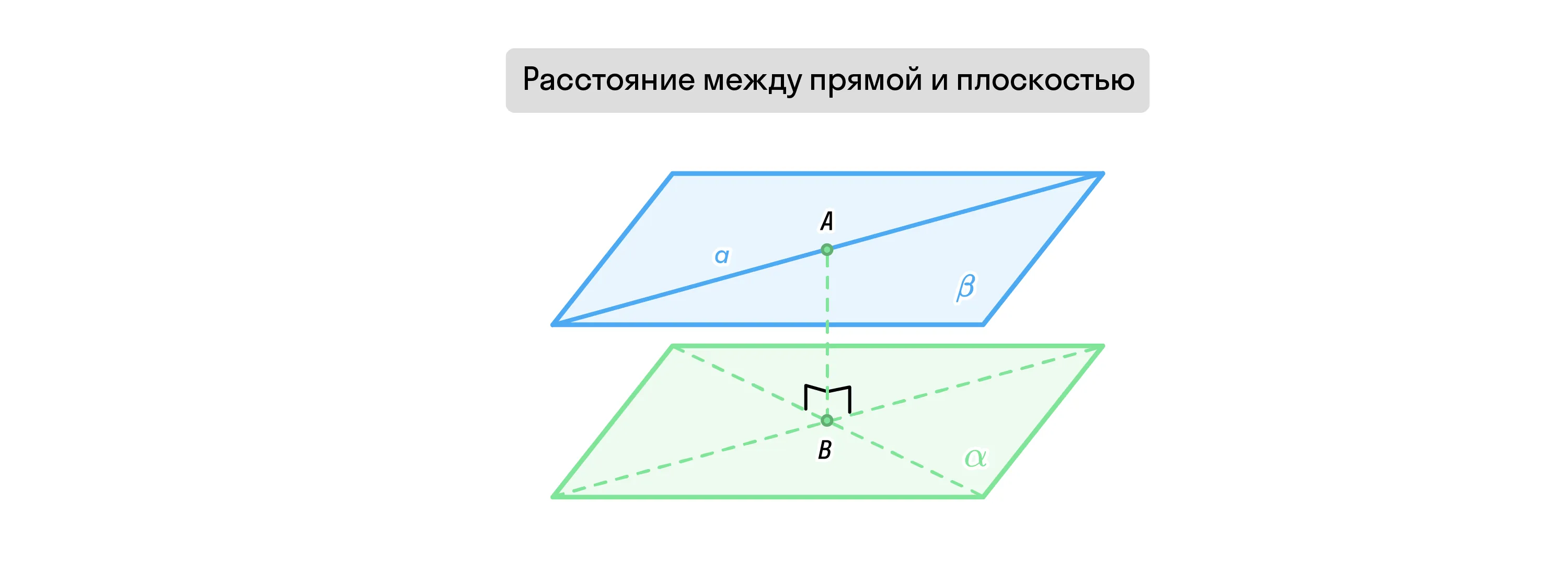
Есть всего два варианта: прямая а принадлежит плоскости α1 и пересекает её. Второе не удовлетворяет условию, т. к. тогда она пересекала бы и плоскость α. А т. к., согласно теореме о расстоянии между параллельными плоскостями, все их точки равноудалены друг от друга, то все точки прямой а, которая принадлежит плоскости α1, также равноудалены от плоскости α. Что и требовалось доказать.
Отточить навыки решения задач с расстоянием между прямой и параллельной ей плоскостью можно в Тренажёре ЕГЭ. Там найдутся все типы заданий на эту тему. Они доступны бесплатно и без ограничений.
