Что такое круглые тела
Круглые тела (тела вращения) — это геометрические тела, которые образованы через вращение плоской фигуры вокруг её стороны или диаметра.
Конус, цилиндр и шар относятся к таким телам.
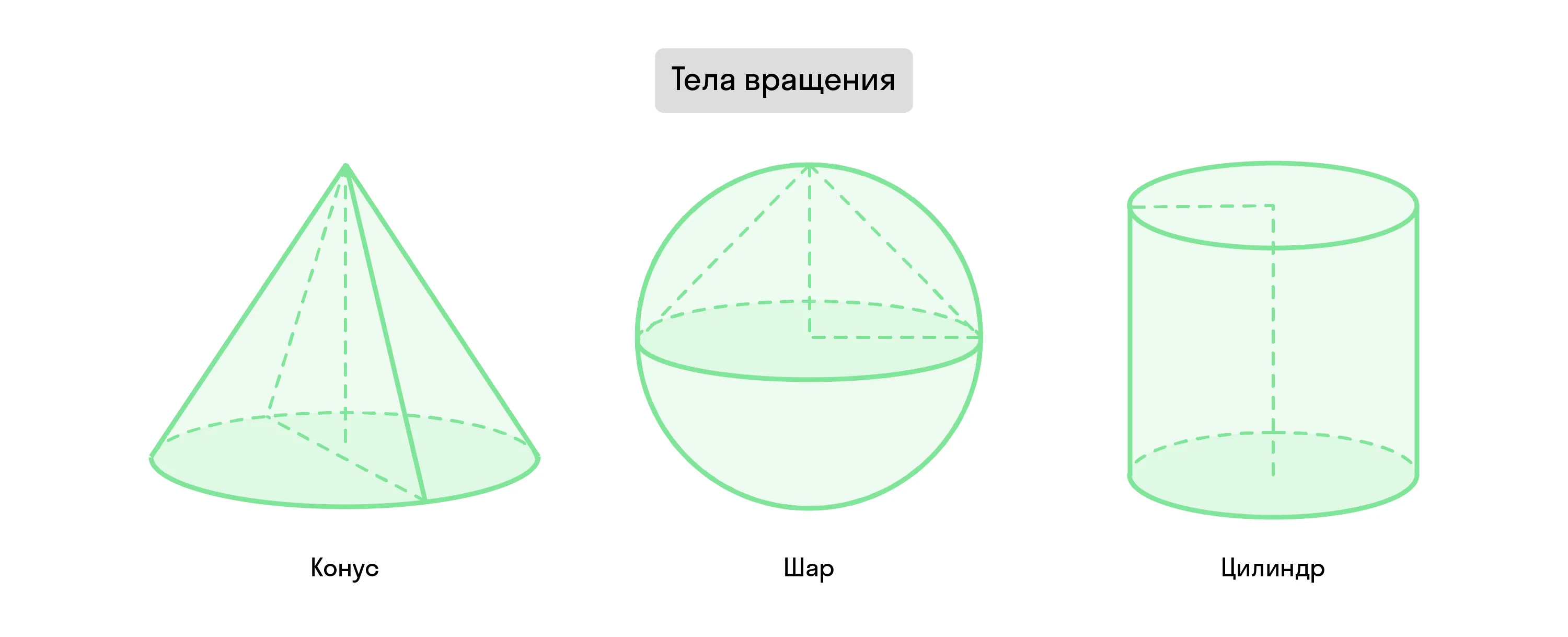
Цилиндр и его свойства
Цилиндр — это тело вращения, которое получается вращением прямоугольника вокруг одной из своих сторон.
Прямая, которая содержит эту сторону, находится в центре цилиндра и называется осью вращения. Во время вращения перпендикулярные оси́ стороны прямоугольника образуют два одинаковых круга — сверху и снизу фигуры. Их называют основаниями цилиндра.
Также из параллельной оси вращения стороны образуется цилиндрическая или боковая поверхность. Отрезки, из которых она составлена, называются образующими.
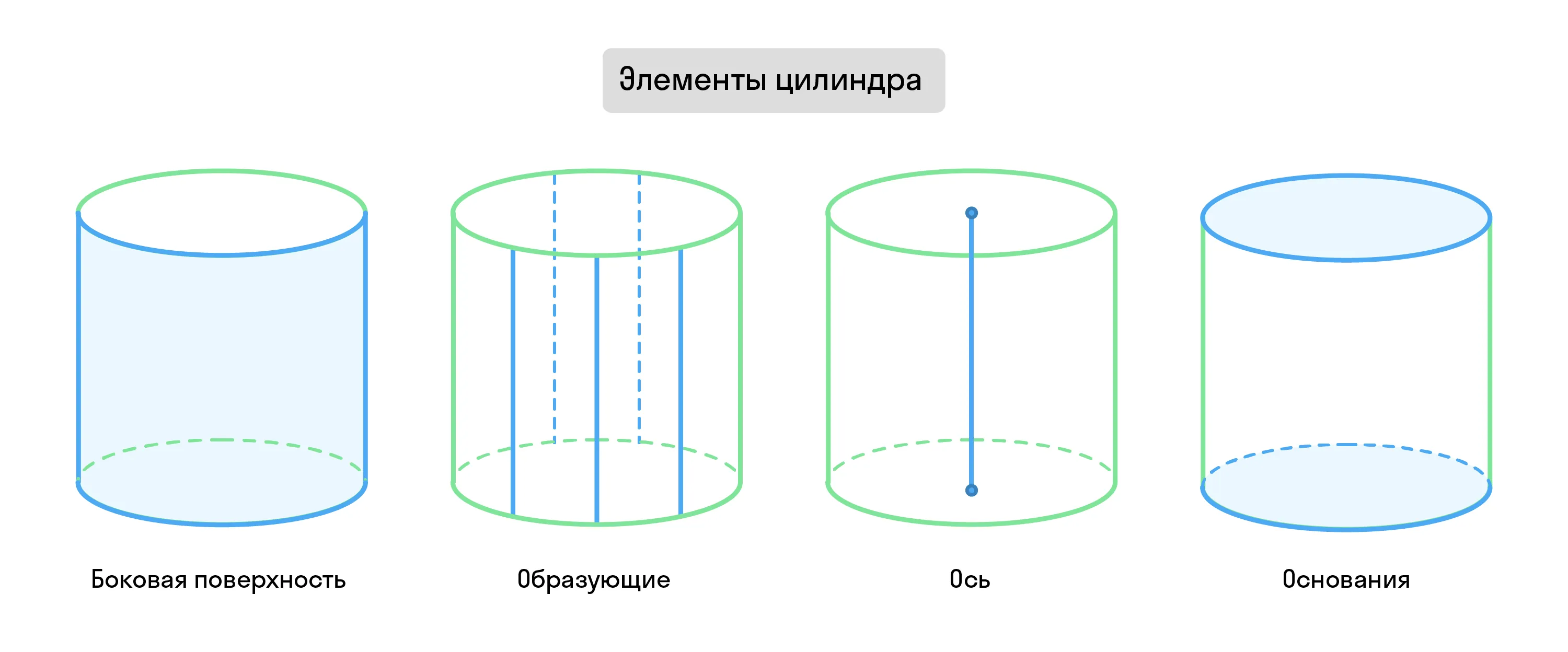
Цилиндр, в основании которого лежит круг, называется круговым.
Но есть и другие, например, эллиптические, в основаниях которых лежат эллипсисы. Также существуют параболические и гиперболические цилиндры.
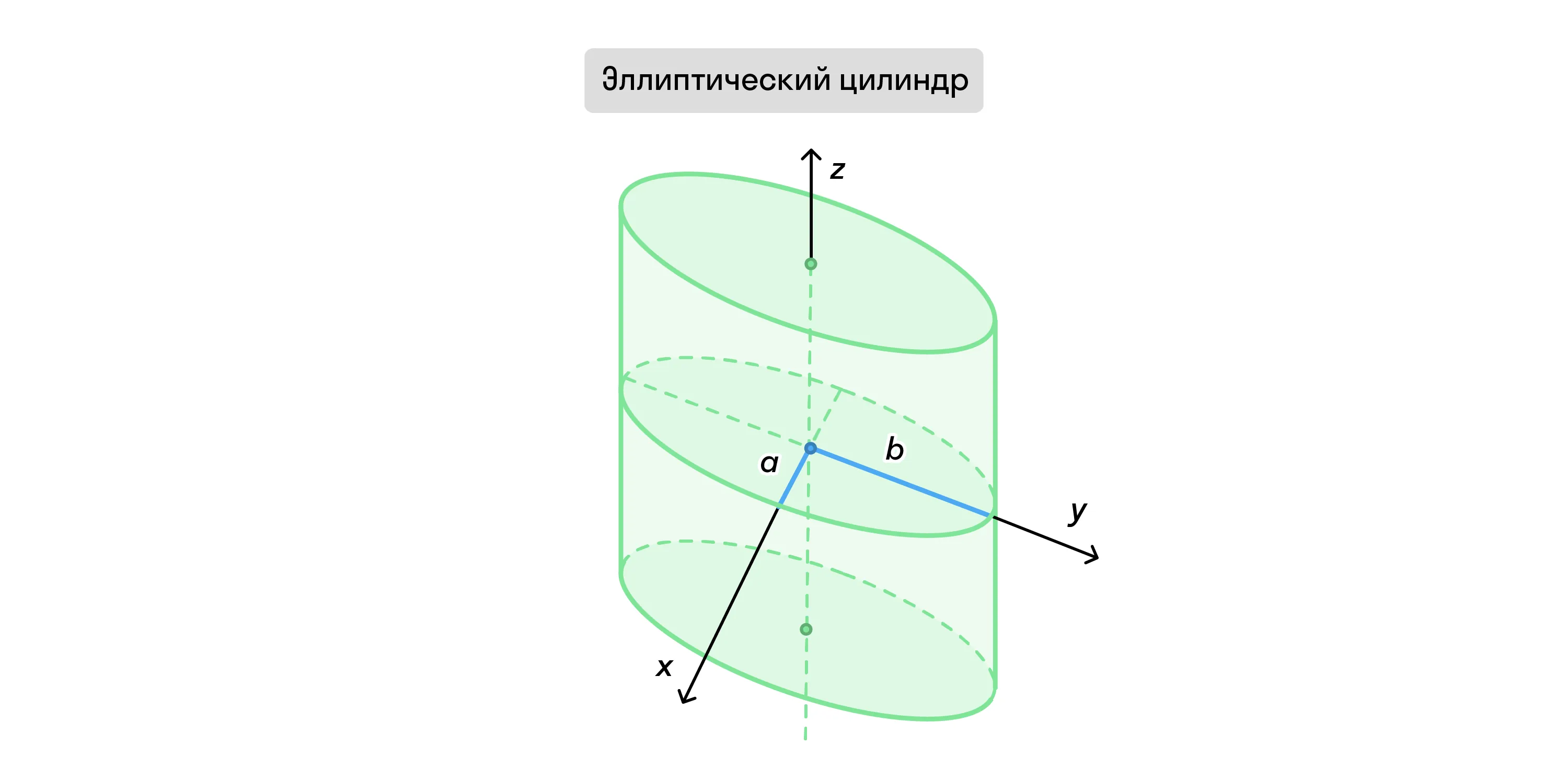
Если образующие цилиндра перпендикулярны плоскости его основания, его называют прямым. В остальных случаях — наклонным.
При этом основания прямого и наклонного цилиндров лежат в параллельных плоскостях. Если всё иначе, цилиндр называют косым.
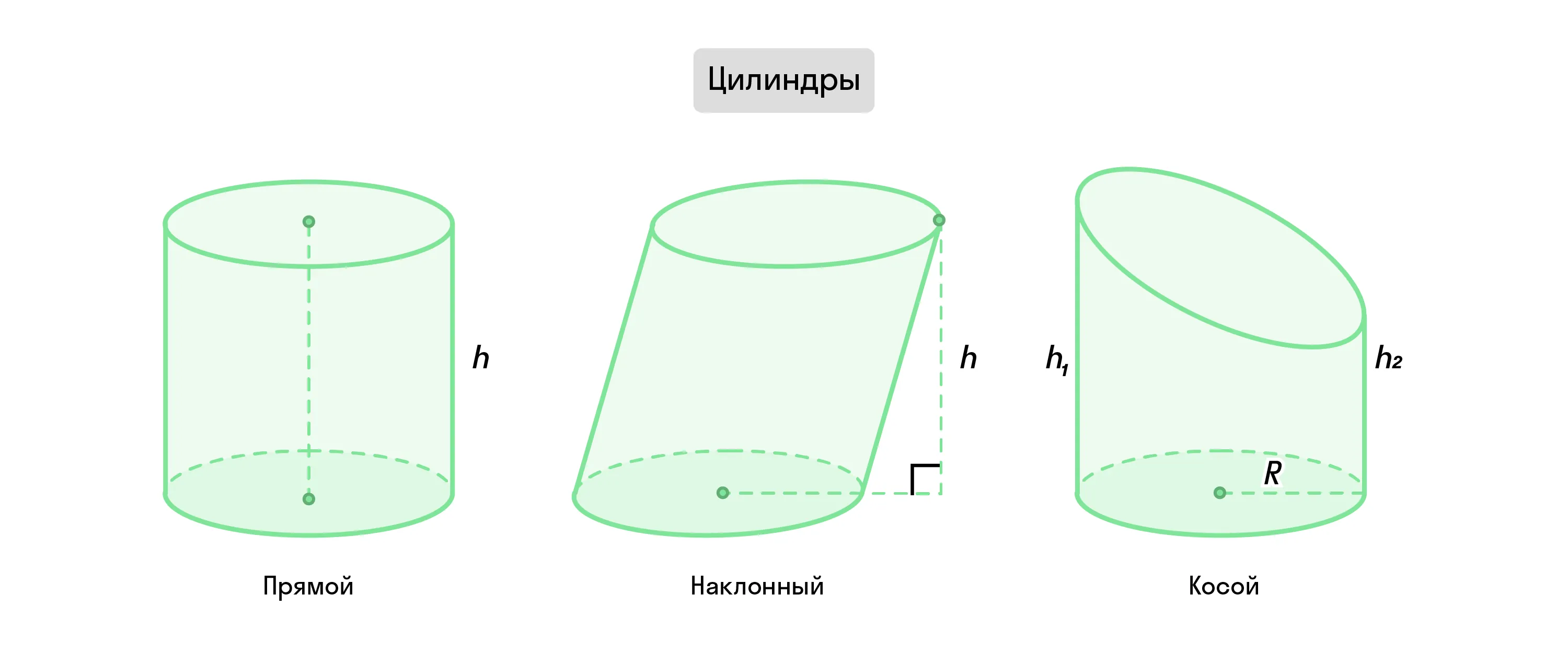
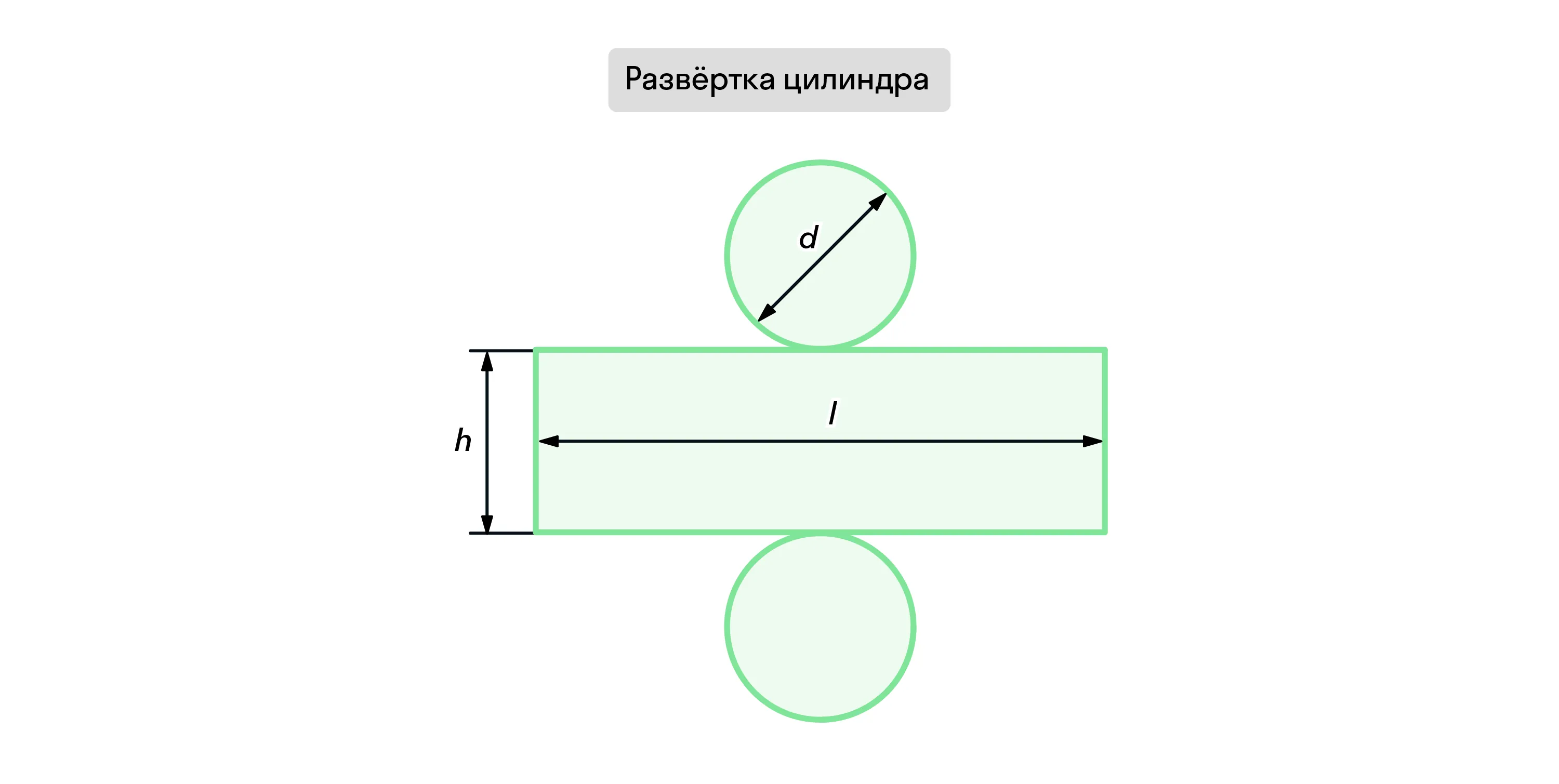
При решении задач может быть полезно сделать развёртку цилиндра. Для этого нужно представить, что вы отделяете от фигуры основания, а в боковой поверхности делаете надрез по образующей так, чтобы она превратилась в прямоугольник.
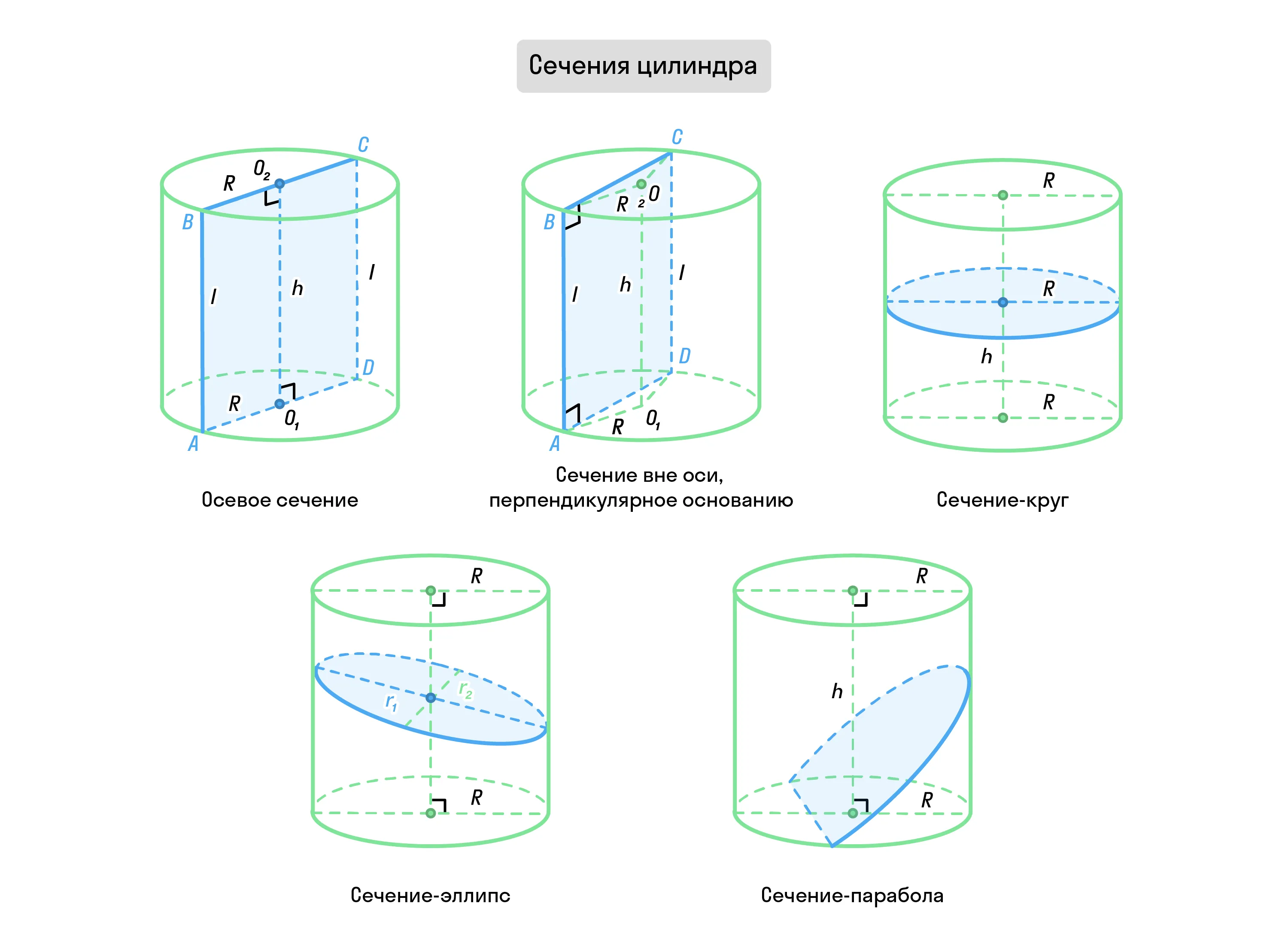
Сечения цилиндра
Осевое сечение цилиндра — это прямоугольник, который образован в результате пересечения фигуры плоскостью, проходящей через её ось.
Если секущая плоскость проходит не по оси цилиндра, но при этом перпендикулярна его основаниям, то сечение — это также прямоугольник.
В случае, когда секущая плоскость параллельна основаниям цилиндра, само сечение — это идентичный его основаниям круг. Если же цилиндр пересекает плоскость, которая не параллельна его основаниям и не касается ни одной из них, то сечением — это эллипс.
Если секущая плоскость пересекает одно из оснований цилиндра, сечением будет парабола или гипербола.
Получи больше пользы от Skysmart:
-
Подготовься к ОГЭ на пятёрку.
-
Подготовься к ЕГЭ на высокие баллы.
Записывайся на бесплатные курсы для детей.
Решай задания в бесплатном тренажёре ЕГЭ.
Конус и его свойства
Конус — это тело вращения, которое получается вращением прямоугольного треугольника вокруг одного из катетов.
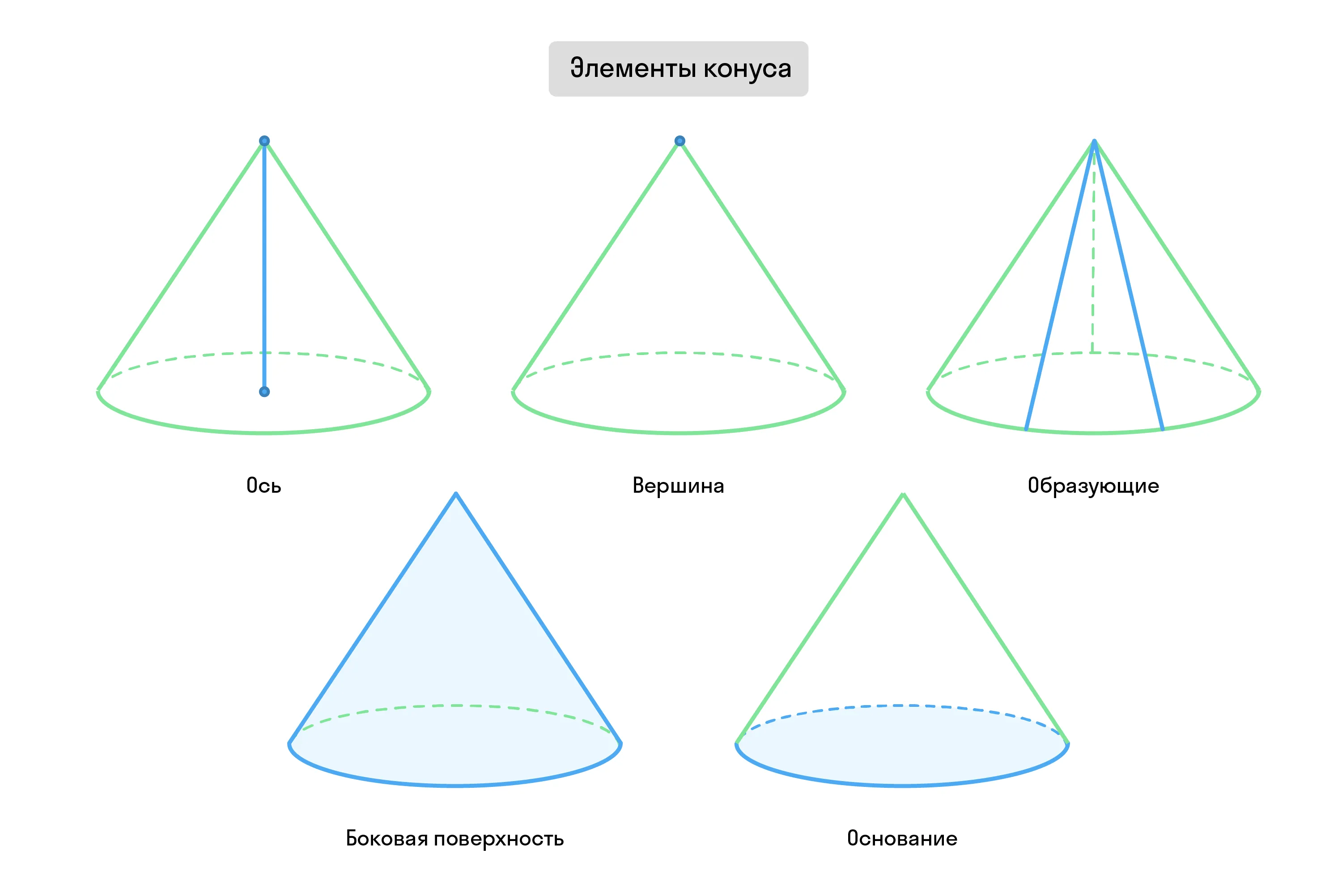
Прямая, которая содержит этот катет, называется осью конуса. При вращении катета, перпендикулярного оси, образуется круг — основание конуса. Гипотенуза при этом формирует коническую или боковую поверхность. Отрезки, из которых она состоит, называются образующими. Вершина вращаемого треугольника также является вершиной конуса.
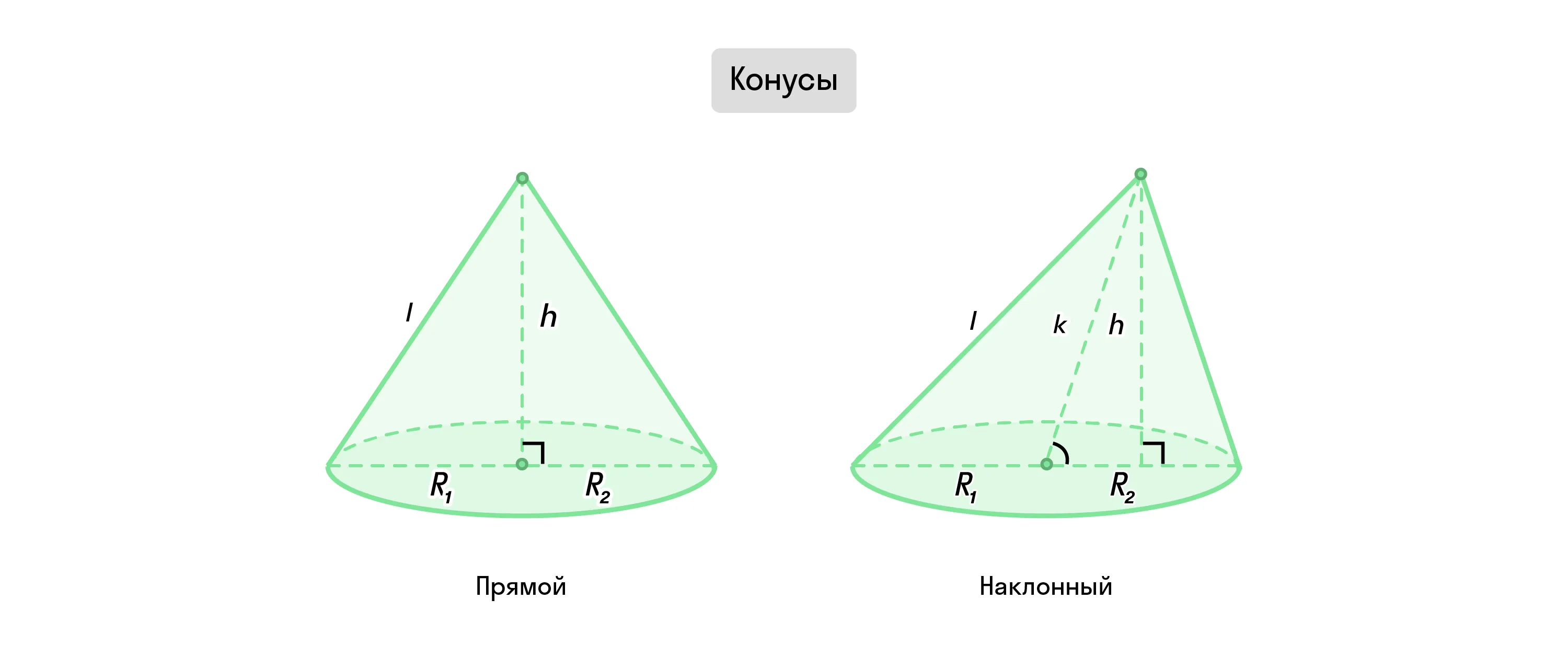
Если перпендикуляр, опущенный из вершины конуса к его основанию, т. е. высота фигуры совпадает с центром этого основания, конус называют прямым. В противном случае — наклонным.
Все образующие прямого конуса равны между собой, а его ось вращения совпадает с высотой. В случае с наклонным, чем дальше образующая от опущенной из вершины высоты, тем она длиннее.
Как и в случае с цилиндром, чтобы решить некоторые задания с конусом, нужно будет сделать его развёртку. Для этого представим, что боковую поверхность разрезали по образующей и развернули. Если добавить к полученной области круг основания, то получится развёртка конуса.
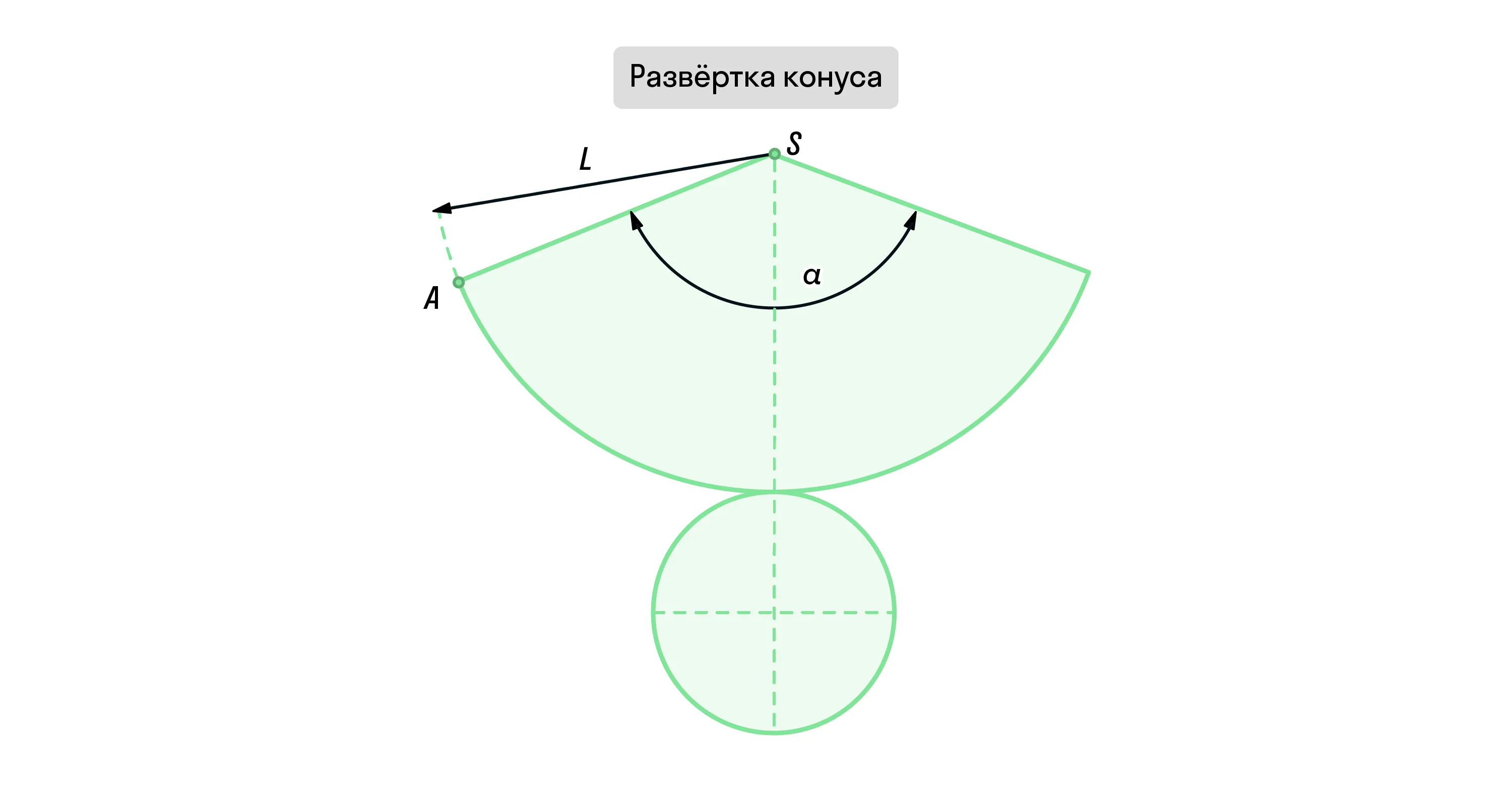
Сечения конуса
Осевое сечение конуса — это треугольник, который образован в результате пересечения фигуры плоскостью, проходящей через её ось.
Если конус пересекает плоскость, проходящая через его вершину не по оси вращения, сечение также будет треугольником.
Если секущая плоскость проходит через цилиндр параллельно его основанию, сечение будет кругом. Тогда образуется усечённый конус — его часть, которая находится между основанием конуса и параллельной ему плоскостью сечения.
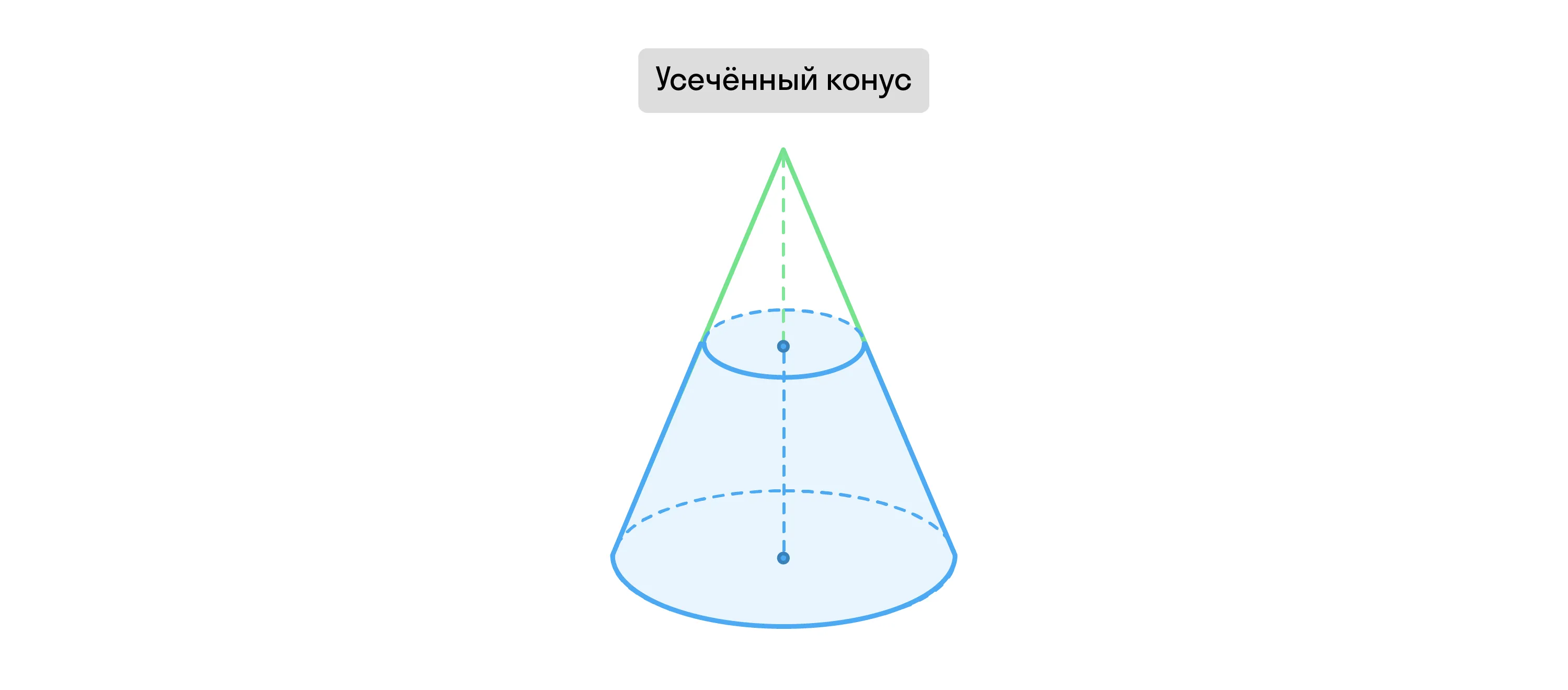
Если же плоскость проходит через цилиндр не параллельно его основанию, тогда сечение может быть эллипсом, параболой или гиперболой. Это зависит от того, пересекает ли она основание фигуры.
|
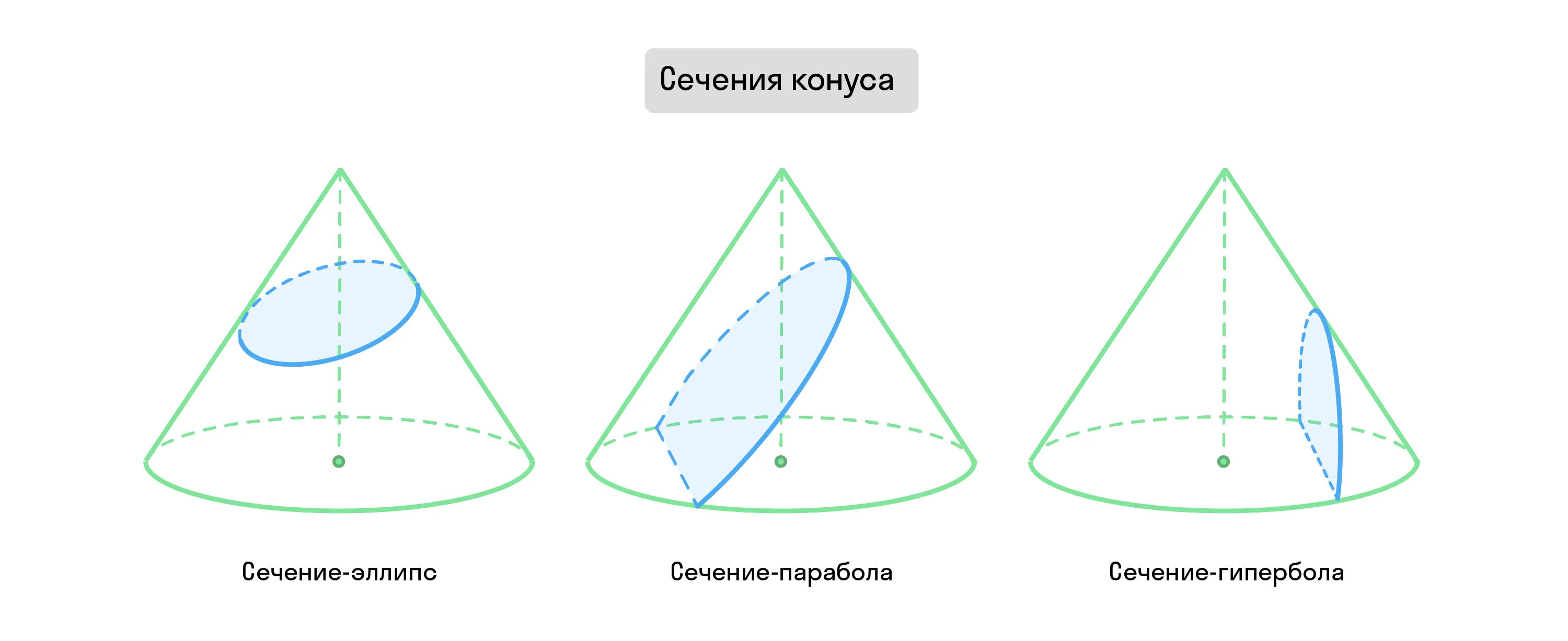
Конус: все основные формулы |
|
|---|---|
|
Объём кругового конуса через R — радиус основания и h — высоту |
|
|
Площадь боковой поверхности R — радиус основания и l — длину образующей |
|
|
Площадь полной поверхности |
|
|
Объём любого конуса |
|
|
Объём усечённого конуса, где S1 и S2 — площади меньшей и большей основы, а H и h — расстояние от вершины конуса до центра нижней и верхней основы. |
|
Шар и его свойства
Шар — это тело вращения, которое получается вращением полукруга вокруг своего диаметра.
У шара нет ни основания, ни вершин. Только центр — точка, равноудалённая от всех точек на поверхности фигуры, и сама поверхность — сфера.
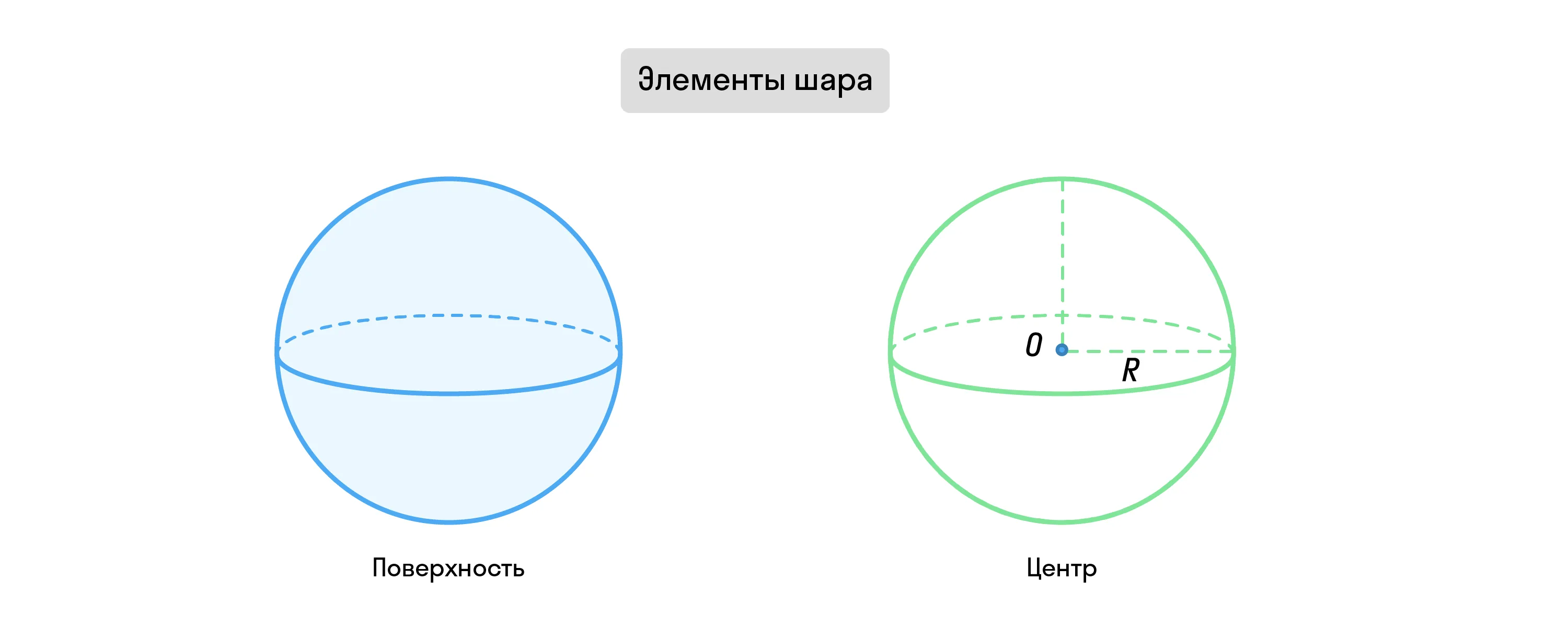
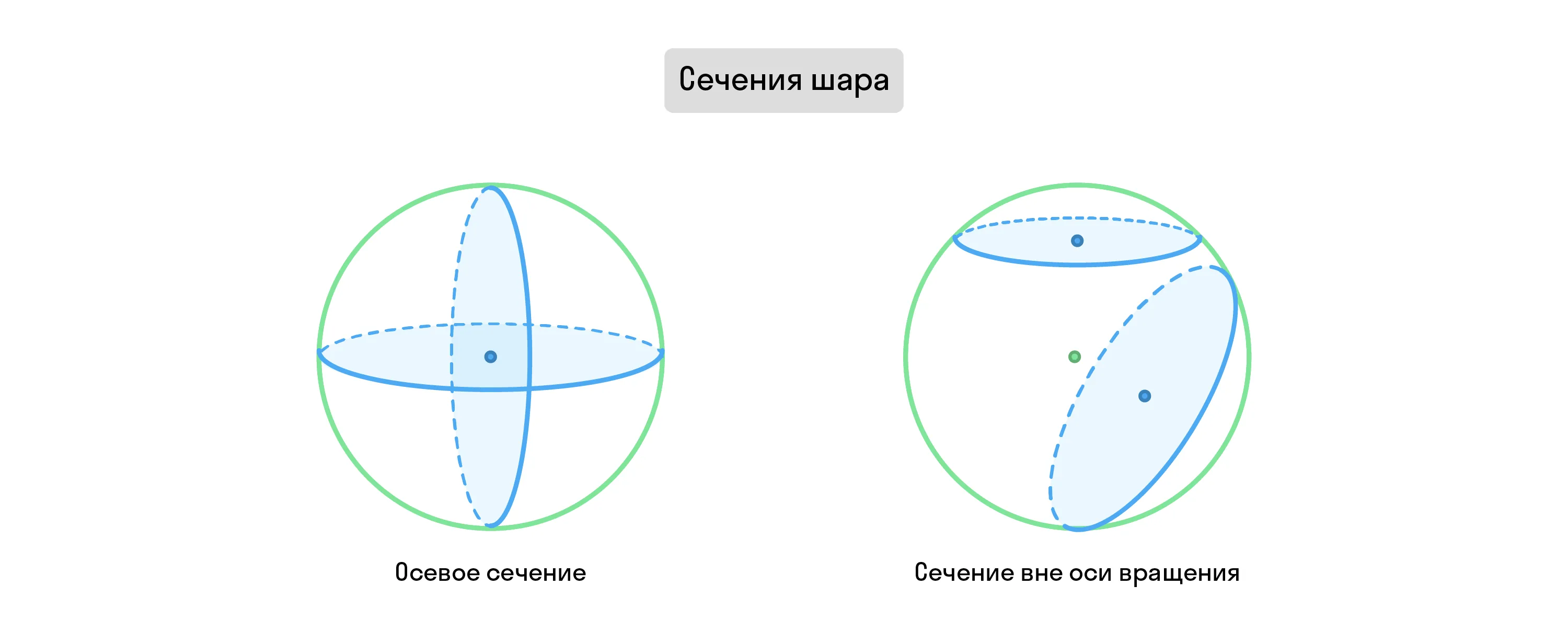
Осевое сечение шара — это круг, который образован в результате пересечения фигуры плоскостью, проходящей через её ось.
При этом, даже если пересекающая фигуру плоскость не будет проходить через её ось, сечение всё равно будет кругом. Таково одно из свойств шара.
|
Шар: все основные формулы |
|
|---|---|
|
Объём шара через радиус |
|
|
Объём шара через диаметр |
|
|
Площадь поверхности шара (сферы) через радиус |
|
|
Площадь поверхности шара (сферы) через диаметр |
|
Проверить, насколько хорошо вы знаете определения, свойства и формулы для задач с круглыми телами, можно в Тренажёре ЕГЭ. Мы собрали там все типы экзаменационных заданий по стереометрии. В Тренажёре также есть автопроверка ответов, а пользоваться им можно бесплатно!
