Для кого эта статья:
- Люди, интересующиеся геометрией или математикой
- Студенты или школьники, изучающие основы черчения или дизайна
- Специалисты в области архитектуры и инженерии
Что такое плоскость
Мы думаем, что вы уже знаете значение слова «плоскость» из уроков геометрии. Возможно, вы слышали его, но плохо представляете, что это такое. Также с этим понятием мы сталкиваемся и в нашей обычной, нематематической жизни. Подумайте, какой предмет мы называем плоским. Верно: тот, который не имеет объема и включает в себя только два измерения — длину и ширину. Любители комиксов, манги и компьютерных игр точно знают понятие «2D», которое ставят в противовес объемному, современному «3D».
Если прошлый абзац был вам совсем непонятен, следующий пример исправит ситуацию. Представьте себе лист бумаги, поверхность пола, стен или стола. В данном случае мы можем убрать слово «поверхность» и заменить его на «плоскость», но будет один нюанс. Площадь этих предметов ограниченна, в то время как плоскость бесконечна, не имеет каких-либо краев или границ.
Итак, пришло время сформулировать определение плоскости:
В другом источнике определение плоскости звучит так:
Советуем запомнить обе формулировки, так как первая подсказывает нам некоторые свойства плоскости — их мы обсудим чуть позже. Вторая же дает нам понять суть этого слова.
Плоскость — это одно из фундаментальных, т. е. основных, понятий в геометрии наряду с точкой и прямой. Можно сказать, что эти три слова связаны друг с другом, как лучшие друзья, и у них множество совместных «историй». Ни одна аксиома, теорема или другое геометрическое понятие не существует отдельно от этих трех.
Из плоскостей математики собирают объемные фигуры. Так, куб состоит из 6 граней, каждая из которых представляет собой часть отдельной плоскости. По этому же принципу мы можем сказать, что правильная пирамида состоит из 4 таких частей, а четырехугольная пирамида — из 5. Кстати, раздел геометрии, который изучает фигуры на плоскости, называется планиметрия, а изучающий объемные фигуры — стереометрия.
Как обозначается плоскость
На уроках геометрии вы будете часто рисовать плоскости и решать связанные с ними задачи. На чертеже плоскость чаще всего изображают в виде параллелограмма или произвольной замкнутой области. Для обозначения плоскости используют строчные буквы греческого алфавита — α, β, γ и т. д.:
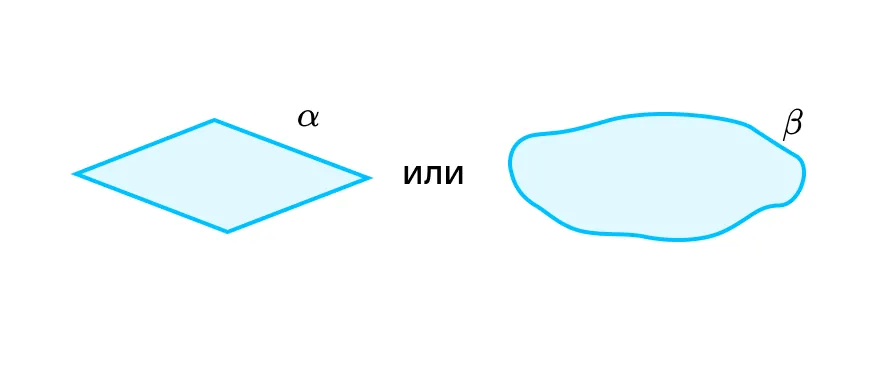
Вот мы и узнали, что такое плоскость в математике. Идем дальше!
Какие бывают виды плоскостей
Самым любопытным из вас может стать интересно, все ли плоскости одинаковые и какие бывают виды плоскостей. Ответы на эти вопросы вы обязательно получите в вузе на предмете начертательная геометрия, если выберете математический профиль. Но ждать придется долго, а ответ хочется получить сейчас, поэтому мы немного приоткроем завесу тайны.
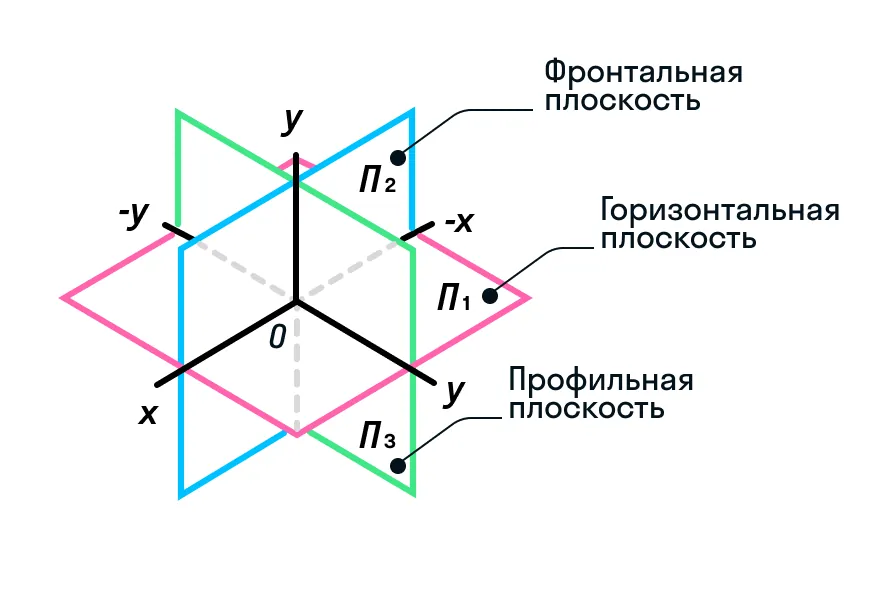
На рисунке показаны три вида плоскостей в трехмерном пространстве, которое еще называют xyz по трем координатным осям.
Горизонтальная плоскость — это та плоскость, которой принадлежит ось Ox, расположенная горизонтально.
Фронтальная плоскость — это плоскость, которая расположена вертикально перед зрителем.
Профильная плоскость — это плоскость, расположенная вертикально и пересекающаяся под прямым углом с горизонтальной и фронтальной.
Повторим, что такая классификация — это лишь дополнительный материал для самых любопытных математиков, им можно удивить учителя или взять его на самостоятельное исследование или даже научный проект.
Как плоскость и точка могут располагаться относительно друг друга
Чтобы было проще понять, давайте сравним плоскость и точку с вами и вашим домашним питомцем. Вы можете или находиться вместе в одной комнате, или быть раздельно, не видеть друг друга. Этот пример наглядно показывает взаимоотношения прямой и плоскости: точка может принадлежать плоскости, а может и не принадлежать ей.
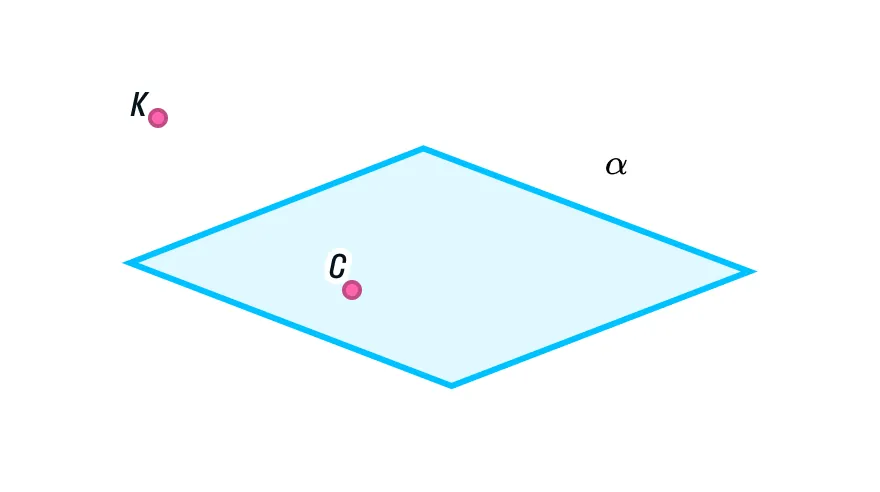
Допустим, в плоскости α есть точка С. Тогда мы можем записать это так: C ∈ α. Возьмем другую точку K, которая лежит вне плоскости. Для записи этой информации используем другой знак — ∉: K ∉ α, иными словами, точка K не принадлежит плоскости α.
Чтобы узнать больше о том, как располагаются точки и плоскости относительно друг друга, нам нужно познакомиться с тремя аксиомами.
Представьте себе бескрайний пляж с бесконечным множеством песчинок. Подобно ему, любая плоскость имеет множество точек, даже если они не обозначены на рисунке.
Эту аксиому можно считать способом задать плоскость в пространстве. Вы и сами можете это сделать — просто поставьте на листе бумаги три точки: M, L и N. Поздравляем, только что вы задали через них новую плоскость, которую можно назвать в честь этих точек, — плоскость MLN. Усложним задачу: теперь с помощью фломастера поставьте пару точек на полу и одну на стене. Вуаля, новая плоскость готова! Только не забудьте стереть ваш чертеж до прихода родителей.
Кстати, последний эксперимент наталкивает на мысль о том, что плоскость необязательно должна быть ровной, параллельной полу, стенам и так далее. Она вполне может располагаться под углом.
Эта аксиома подтверждает тот факт, что точка может и не принадлежать плоскости. Если мы вернемся к нашему чертежу на бумаге, мы можем поставить еще одну точку на листе. В таком случае эта новая точка будет принадлежать плоскости. Если же мы поставим ее на доске, оконном стекле, подошве своего ботинка, точка не будет принадлежать исходной плоскости.
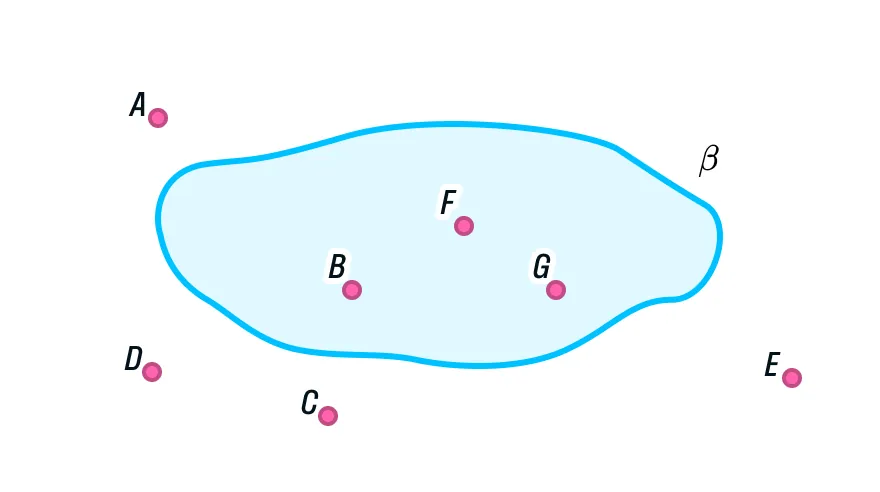
Также множество точек может одновременно принадлежать разным плоскостям в пространстве. Предположим, у нас есть точки A, B, C и D. Давайте узнаем, какие плоскости могут проходить через них.
Принадлежат плоскости |
Не принадлежит плоскости |
|---|---|
ABC |
D |
ABD |
С |
ACD |
B |
BCD |
А |
Получи больше пользы от Skysmart:
-
Прокачивай знания на курсах математики
-
Выбирай из 1200+ репетиторов по математике
Записывайся на бесплатные курсы для детей
Как прямая и плоскость могут располагаться относительно друг друга в пространстве
Есть несколько вариантов, как плоскость и прямая или луч могут взаимно располагаться в пространстве. Давайте разберем подробно каждый из них.
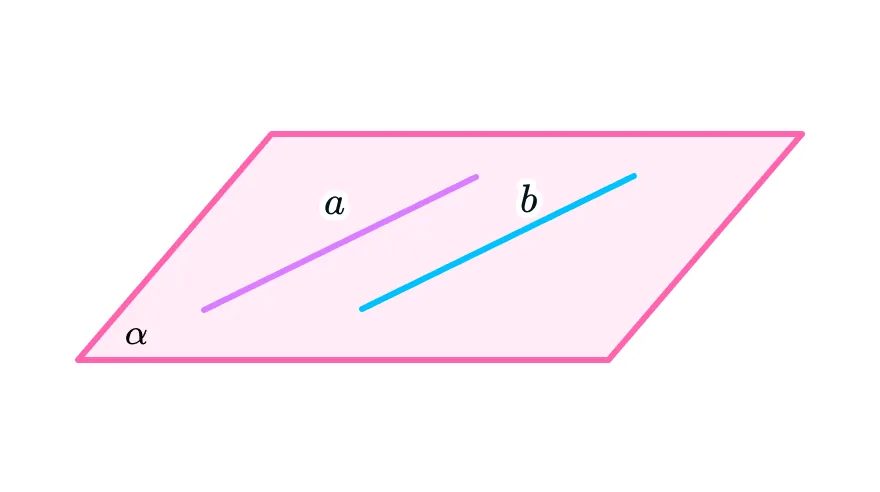
1. Прямая может лежать в плоскости
Здесь все просто. А если на уроках геометрии вы захотите похвастаться своими знаниями, можно добавить: «Если в плоскости лежат хотя бы две точки, которые принадлежат прямой, эта прямая лежит в плоскости». Учитель точно будет в восторге!
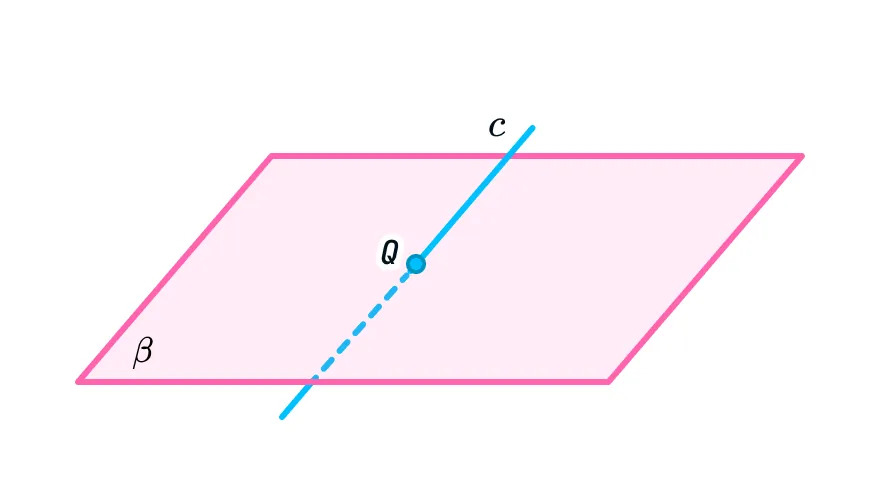
2. Прямая может пересекать плоскость
Проведем эксперимент: возьмем плоскость в пространстве (кружочек колбасы) и пересечем ее насквозь прямой (зубочисткой). Посчитайте, сколько общих точек они будут иметь. Верно, только одну.
В математике пересечение обозначают символом ⋂. Так, c ⋂ β = V означает, что прямая c пересекает плоскость β в точке V.
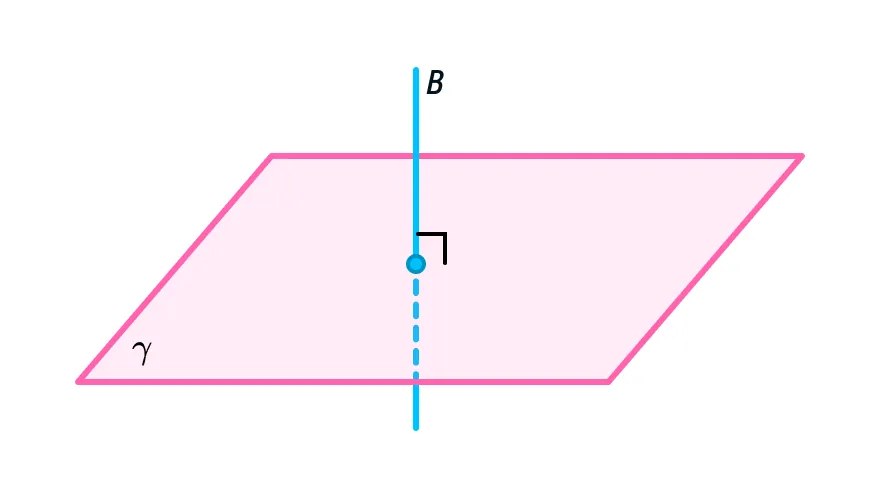
Из опыта с колбасой ясно, что мы можем воткнуть зубочистку разными способами, т. е. под разным углом. Исходя из этого, в геометрии есть понятие угла между прямой и плоскостью, где отдельно отмечается случай перпендикулярности.
Если прямая B перпендикулярна плоскости γ, это можно записать следующим образом: В ⟂ γ.
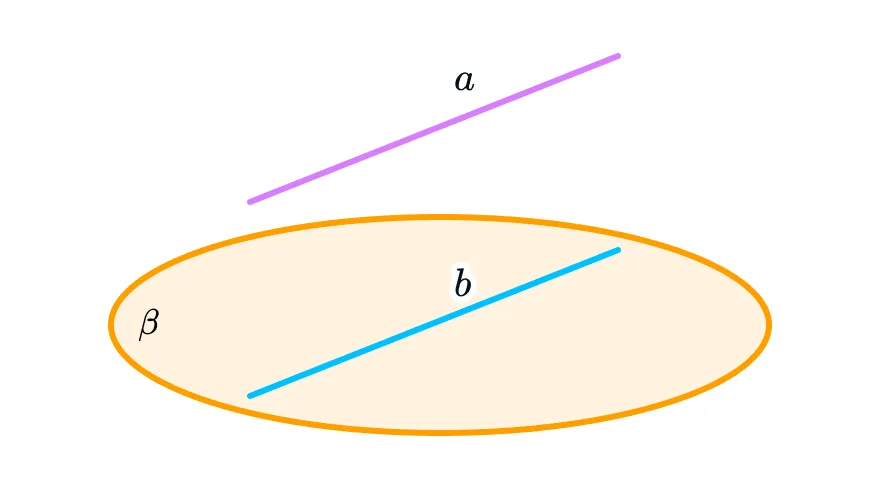
3. Прямая может быть параллельна плоскости
В таком случае прямая и плоскость не будут иметь общих точек. Если прямая D параллельна плоскости γ, это можно записать следующим образом: D || γ.
Подведем краткий итог с помощью таблицы.
Расположение |
Количество общих точек |
|---|---|
Прямая и плоскость параллельны |
0 |
Прямая и плоскость пересекаются |
1 |
Прямая лежит в плоскости |
От 2 до бесконечности |
Как две плоскости могут располагаться относительно друг друга
Следующий пункт нашего обсуждения — это взаимное расположение плоскостей. Прежде чем продолжить читать, остановитесь на секунду и подумайте сами, как могут располагаться в пространстве две плоскости.
Да, вы абсолютно правы! Плоскости могут:
быть параллельны друг другу;
пересекаться, в том числе под углом 90 градусов (в таком случае плоскости могут называться перпендикулярными);
совпадать друг с другом (иметь по крайней мере 3 общие точки).
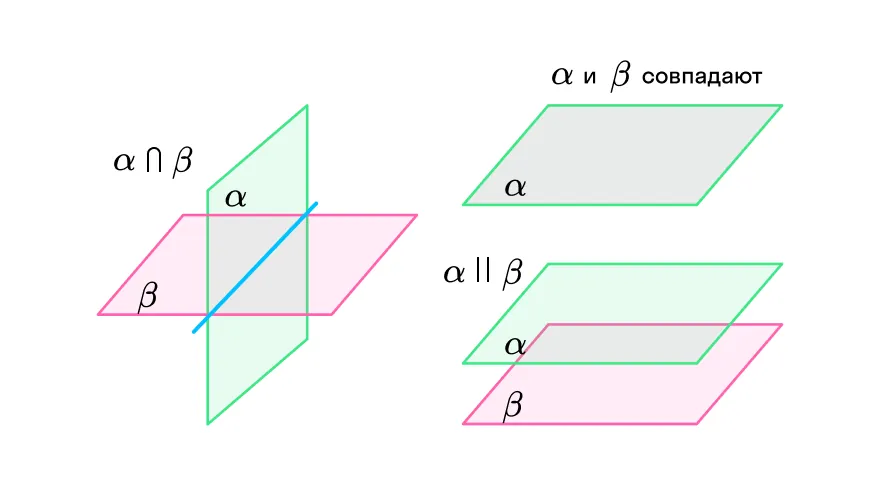
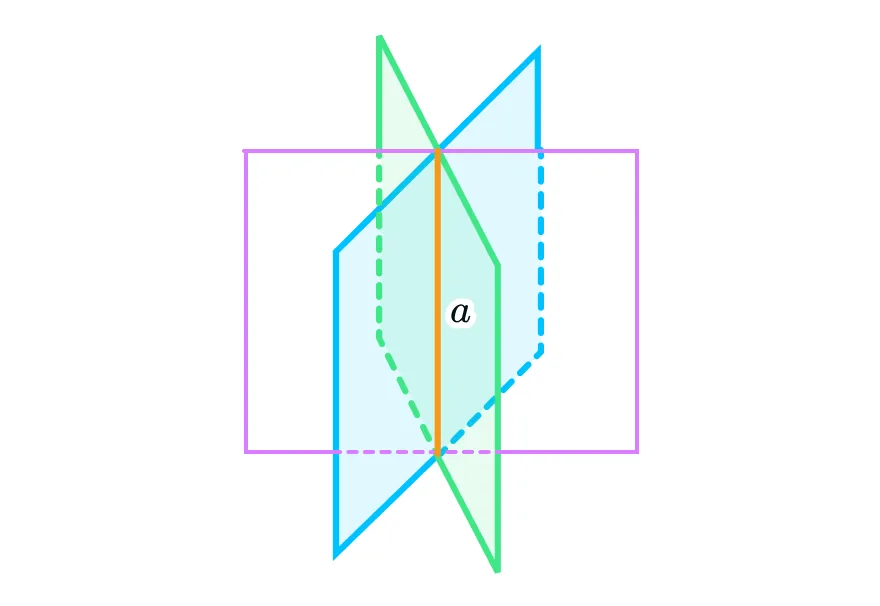
Кстати, это еще не все типы расположений. Дело в том, что множество плоскостей могут пересекаться в одной точке или по одной прямой, но об этом мы расскажем в других статьях. Оставайтесь вместе с нами :)
Как задать плоскость в пространстве
На уроках геометрии учитель может спросить: «А каким образом можно задать плоскость?», и некоторые из ваших одноклассников растеряются. Давайте разберемся, что значит «задать плоскость». По сути, это значит перечислить элементы и способы их расстановки, которые позволяют сказать: «Вот, через них проходит плоскость». Теперь подробнее разберемся, в каких случаях можно утверждать, что плоскость существует.
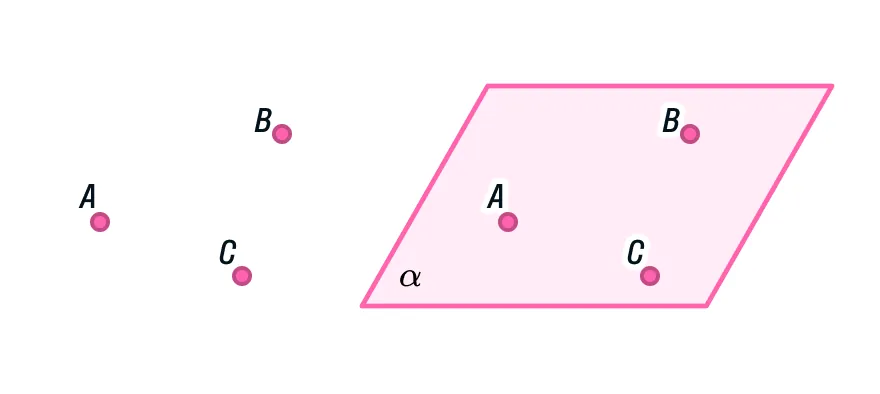
Вернемся к аксиоме. Как мы уже знаем, через три точки, не лежащие на одной прямой, проходит плоскость, причем только одна. А значит, задать плоскость можно через три точки, которые не лежат на одной прямой.

Второй способ вытекает из первого: проведем прямую, соединяющую две точки из трех. Сейчас нашей плоскости принадлежат прямая и точка, не лежащая на ней. Они и задают плоскость.
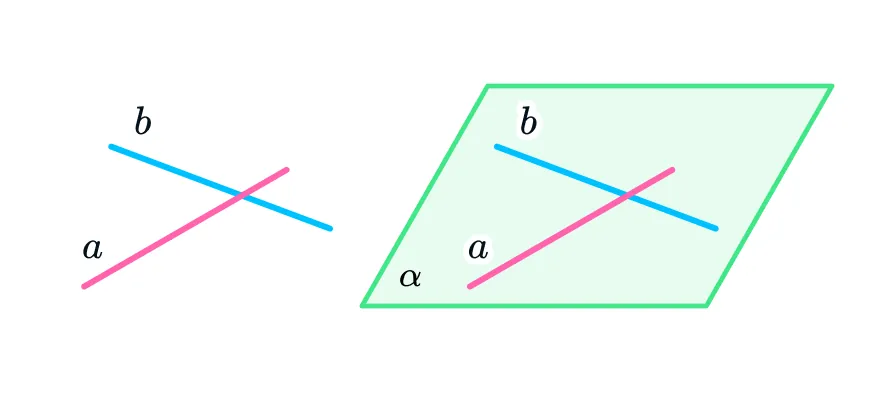
Продолжим соединять точки. На этот раз соединим между собой любые две точки: пусть это будут А и В, А и С. Мы получим две прямые, которые пересекаются друг с другом. Это значит, что плоскость могут задать две пересекающиеся прямые.
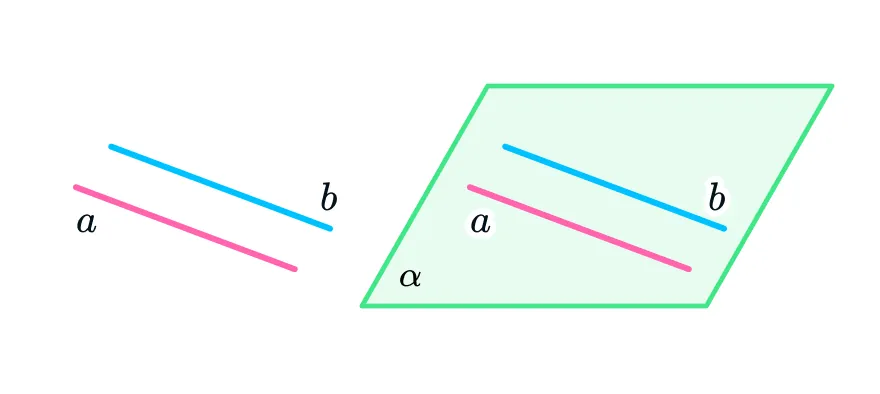
Четвертый способ: плоскость могут задать прямые, параллельные друг другу.
На курсах по профильной математике в школе Skysmart вы познакомитесь с еще более увлекательными темами, получите необходимые сведения для подготовки к контрольным и почувствуете себя настоящим ученым. Ждем вас на занятиях, до скорых встреч!





















