Что такое функция?

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

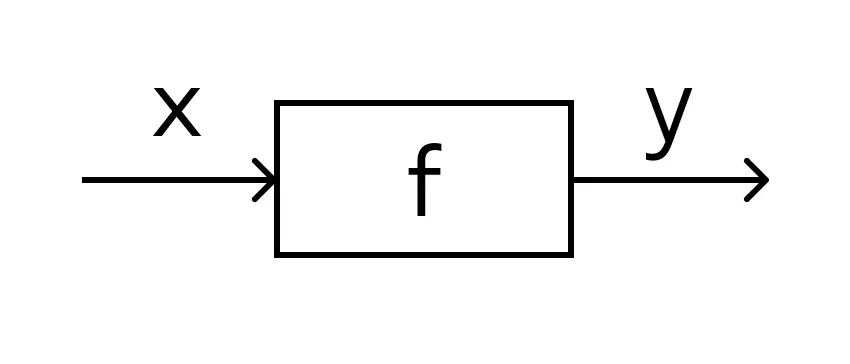
В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, функция у = 2х каждому действительному числу x ставит в соответствие число y, которое в два раза больше, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

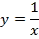
область определения выглядит так:

• х ≠ 0 (потому что на ноль делить нельзя)

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

Рассмотрим другие типы соответствий между множествами.

Например, фрукты и цвет каждого:

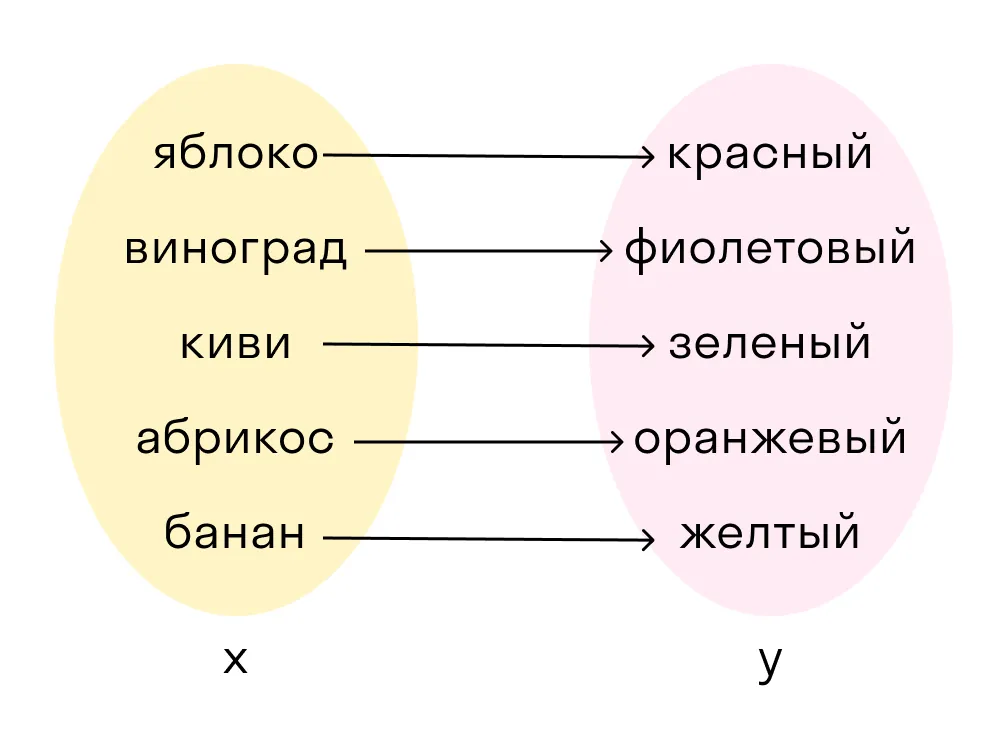
У каждого фрукта есть свой цвет. Но такое соответствие нельзя назвать взаимно-однозначным. Например, яблоко может быть и красным, и желтым и даже зеленым.

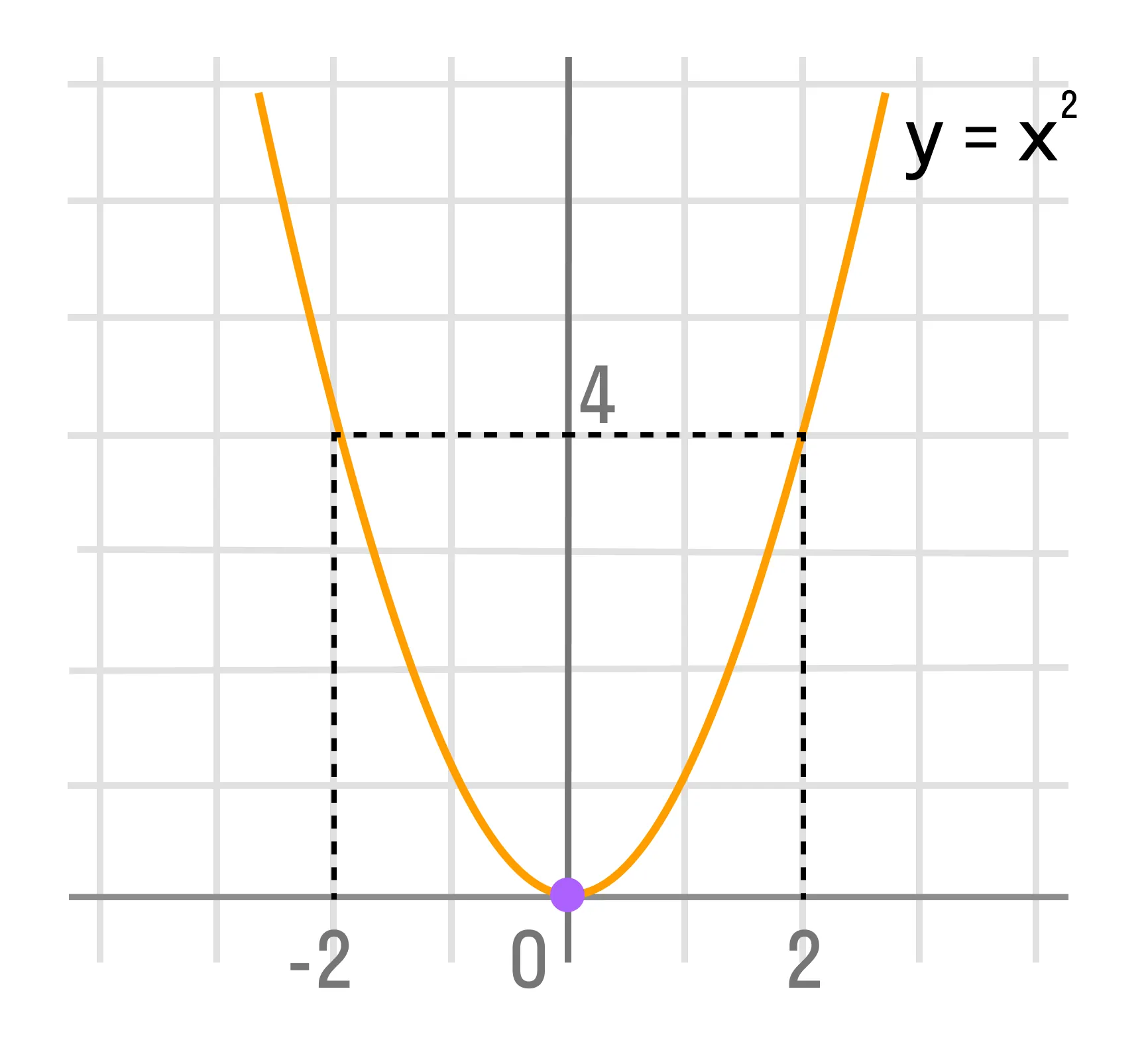
Пример такого соответствия в математике — функция у = х2. Один и тот же элемент второго множества у = 4 соответствует двум разным элементам первого множества: х = 2 и х = -2.

Так на примере с фруктами можно показать соответствие, которое нельзя назвать функцией:

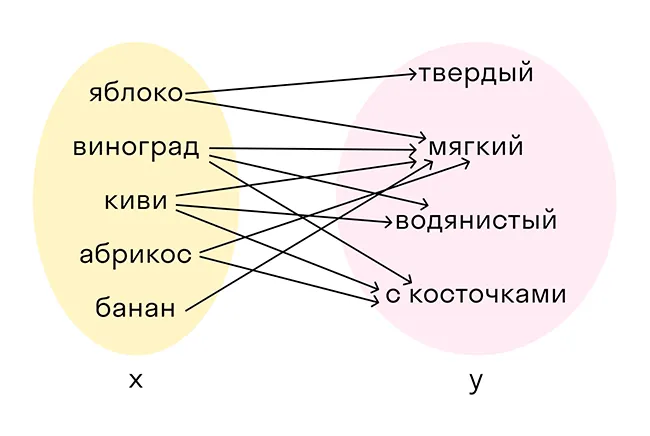
Видно, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества. Описать такое соответствие математически было бы сложнее.

Способы задания функции

Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ — самый наглядный. На графике сразу видно возрастание и убывание функции, наибольшие и наименьшие значения, точки максимума и минимума.
• Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

179.6K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Задать функцию формулой

Через аналитический способ задания функции можно сразу по конкретному значению аргумента «x» найти значение функции «y».

Пример. Дана функция: y(x) = 32x + 5.

Найти: значения функции «y» при x = 0.

Как рассуждаем:

Подставим в формулу вместо «x» число «0». Запишем расчет.

y(0) = 32 * 0 + 5 = 5

Ответ: y = 5.

Задать функцию таблицей

Любую функцию можно записать с помощью таблицы. Для этого достаточно найти несколько значений «y» для произвольно выбранных значений «x».

Пример. Дана функция: y(x) = −x + 4.

Найти: значения «y» при x = -1, x = 0 и x = 1.

Как рассуждаем:

1. Подставим в функцию y(x) = −x + 4 вместо «x» первое число -1.

2. Продолжим подставлять в функцию y(x) = −x + 4 данные значения x (0 и 1).
y(0) = −0 + 4 = 4
y(1) = −1 + 4 = 3

3. Запишем полученные результаты в таблицу:

Так мы получили табличный способ задания функции y(x) = −x + 4.

Задать функцию графиком

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

График функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числовые значения вместо «x».

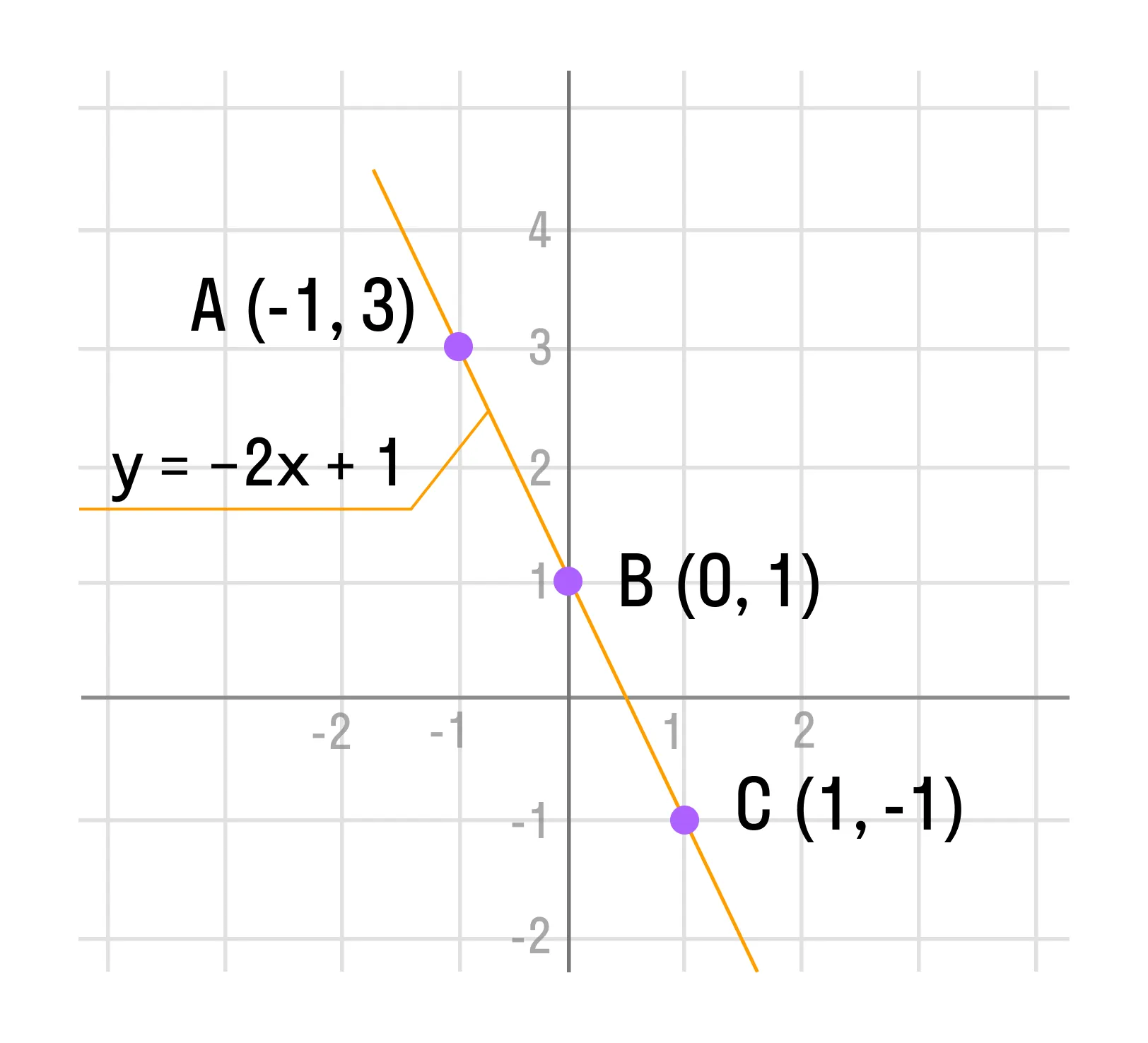
Пример. Дана функция: y(x) = −2x + 1.

Найти: значения «y» для произвольных «x», а именно −1, 0, 1.

Как рассуждаем:

1. Подставим данные значения х в функцию и запишем результаты:

2. Каждая пара значений «x» и «y» — это координаты точек по оси Ox (абсцисса точки) и Oy (ордината точки).

Дадим названия каждой точке и запишем их координаты:

3. Отметим точки А (-1; 3), B (0; 1) и С (1; -1) на прямоугольной системе координат.

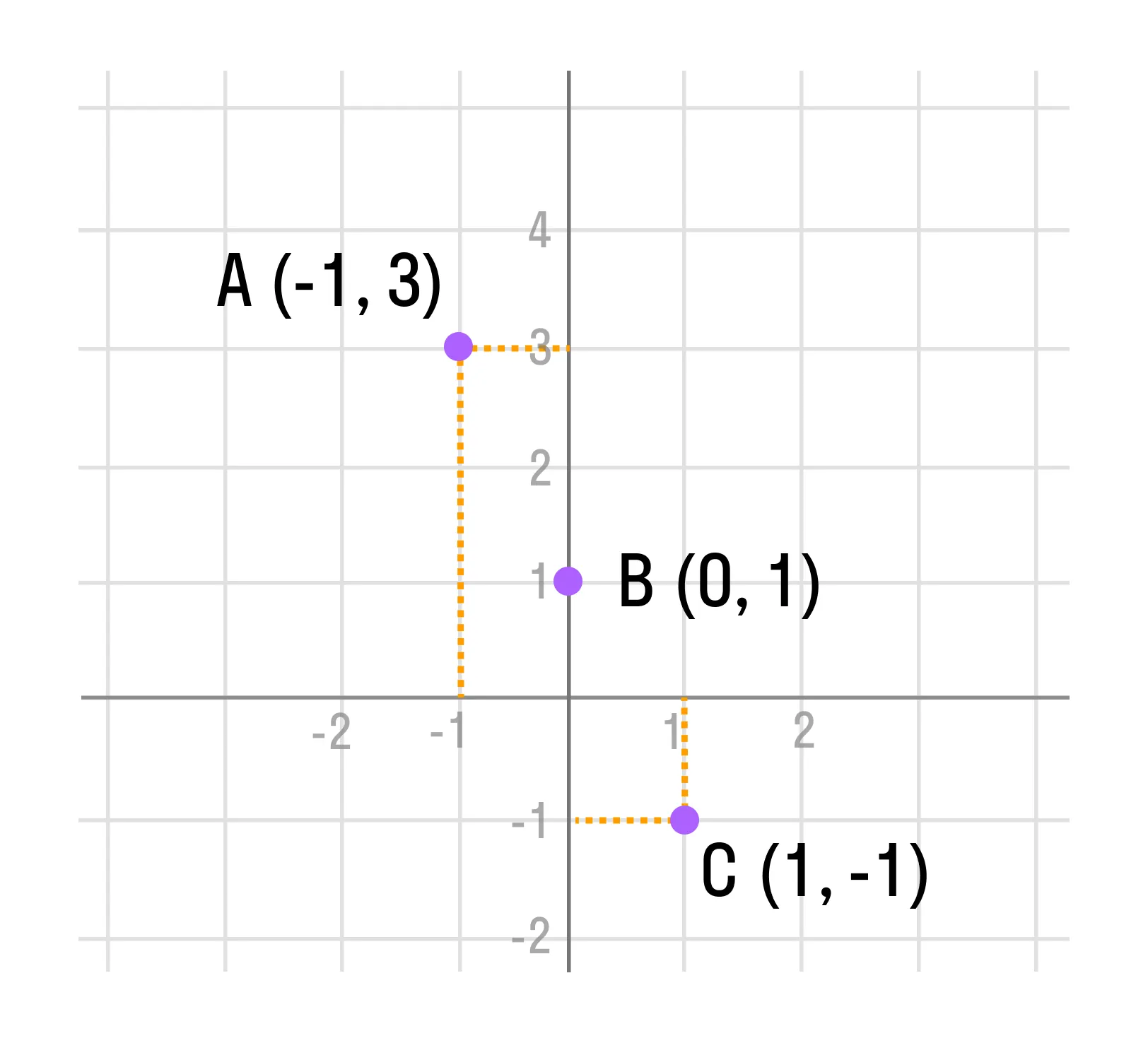
4. Соединим отмеченные точки прямой.

Проведенная прямая будет графиком функции y(x) = −2x + 1.