Квадратичная функция. Построение параболы

Основные понятия

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило, в соответствии с которым каждому значению аргумента соответствует единственное значение функции. Вот какими способами ее можно задать:

• Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ: наглядно.

• Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

График функции — это объединение всех точек координатной плоскости, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.

Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.

Построение квадратичной функции

Квадратичная функция задается формулой y = ax² + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0.

График квадратичной функции — парабола, которая имеет следующий вид для y = x² в частном случае при b = 0, c = 0:

Точки, обозначенные фиолетовыми кружками, называют базовыми точками. Чтобы найти их координаты для функции y = x², нужно составить таблицу:

x	−2	−1	0	1	2
y	4	1	0	1	4

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x² при любых значениях остальных коэффициентов. При увеличении старшего коэффициента график сужается, при уменьшении — расширяется.

График функции y = –x² выглядит, как перевернутая парабола:

Зафиксируем координаты базовых точек в таблице:

x	−2	−1	0	1	2
y	−4	−1	0	−1	−4

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:

• Если старший коэффициент больше нуля (a > 0), то ветви параболы напрaвлены вверх.
• Если старший коэффициент меньше нуля (a < 0), то ветви параболы напрaвлены вниз.

Как строить график квадратичной функции — учитывать значения х, в которых функция равна нулю. Иначе это можно назвать нулями функции. На графике нули функции f(x) — это точки пересечения у = f(x) с осью ОХ.

Так как ордината (у) любой точки на оси ОХ равна нулю, поэтому для поиска координат точек пересечения графика функции у = f(x) с осью ОХ, нужно решить уравнение f(x) = 0.

Для наглядности возьмем функцию y = ax² + bx + c. Чтобы найти точки пересечения с осью Ox, нужно решить квадратное уравнение ax² + bx + c = 0. В процессе найдем дискриминант D = b² - 4ac, который даст нам информацию о количестве корней квадратного уравнения.

Рассмотрим три случая:

1.  Если D < 0, то уравнение не имеет решений и парабола не имеет точек пересечения с осью ОХ. Если a > 0,то график выглядит так:
   

2. Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
3. Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:



Если a > 0, то график выглядит как-то так:

 

Теперь понятно, что, зная направление ветвей параболы и знак дискриминанта, мы можем схематично представить график конкретной функции.

Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

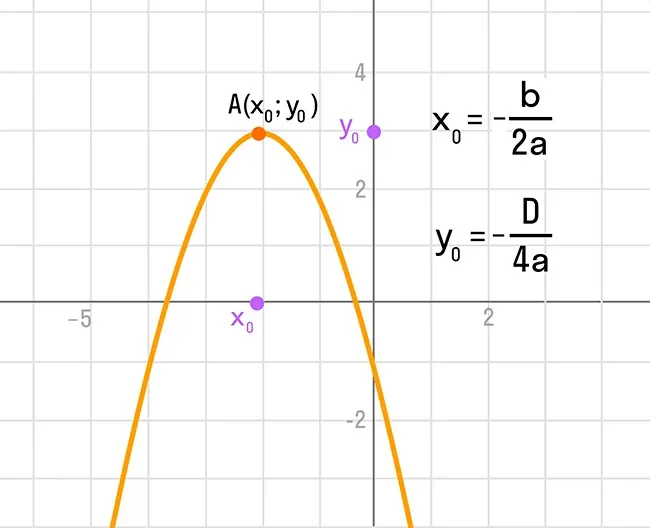
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax² + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции:

 

178.1K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Подготовься к ОГЭ на пятёрку.

• Подготовься к ЕГЭ на высокие баллы.

• Записывайся на бесплатные курсы для детей.

• Решай задания в бесплатном тренажёре ЕГЭ.

Алгоритм построения параболы

Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.

Уравнение квадратичной функции имеет вид y = ax² + bx + c.

Разберем общий алгоритм на примере y = 2x² + 3x - 5.

Как строим:

1. Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена 2x² + 3x - 5.

D = b² - 4ac = 9 - 4 * 2 * (-5) = 49 > 0

√D = 7

В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:

2x² + 3x - 5 = 0

,

3. Координаты вершины параболы:

4. Точка пересечения с осью OY находится: (0; -5) относительно оси симметрии.

5. Нанесем эти точки на координатную плоскость и построим график параболы:

   

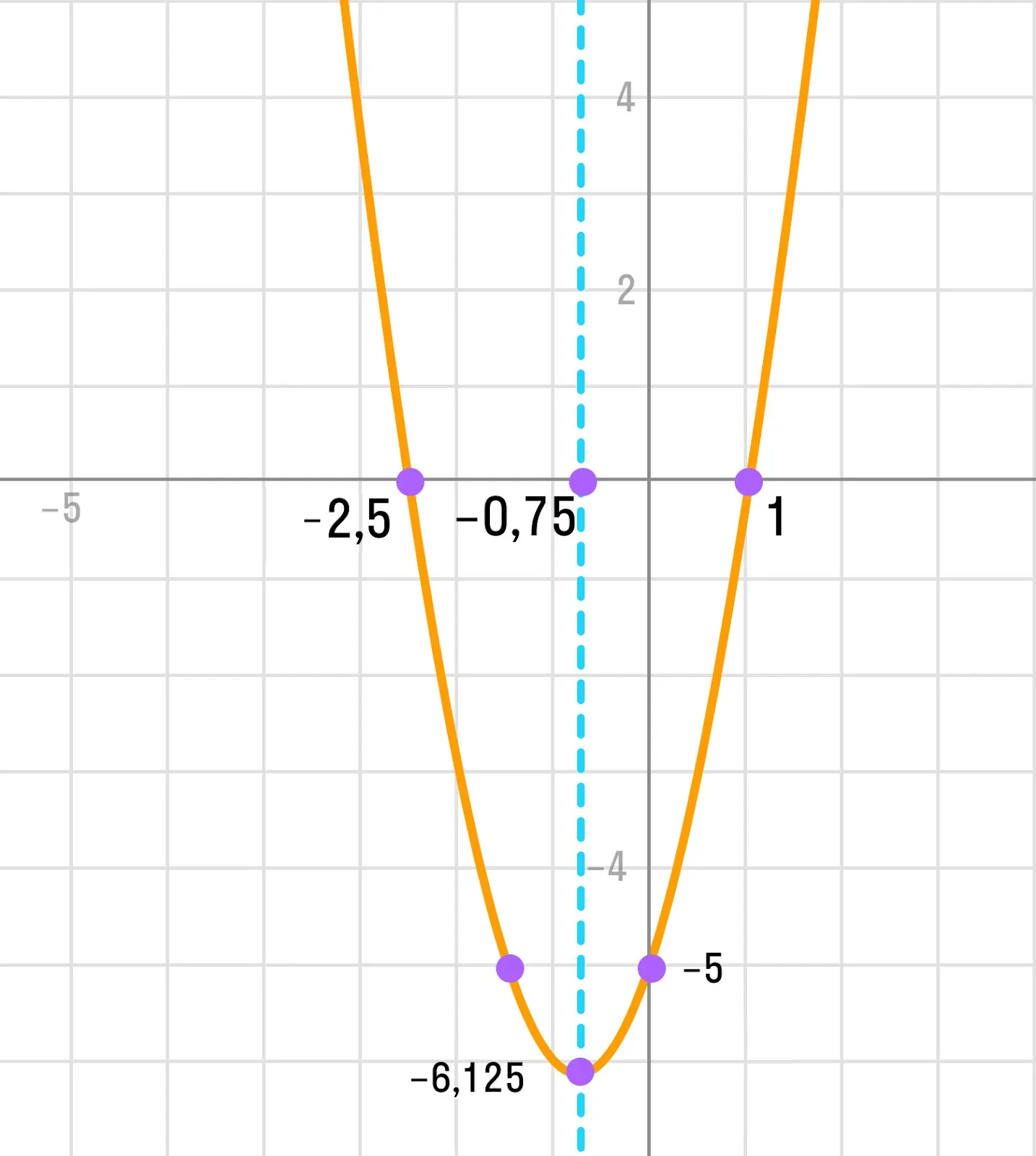
Уравнение квадратичной функции имеет вид y = a * (x - x₀)² + y₀

Зная координаты вершины параболы и старший коэффициент, можно записать уравнение квадратичной функции в виде у = a(x − x₀) + y₀, где x₀, y₀ — координаты вершины параболы.

Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x² + 3x - 5 при а = 1, то второй коэффициент является четным числом.

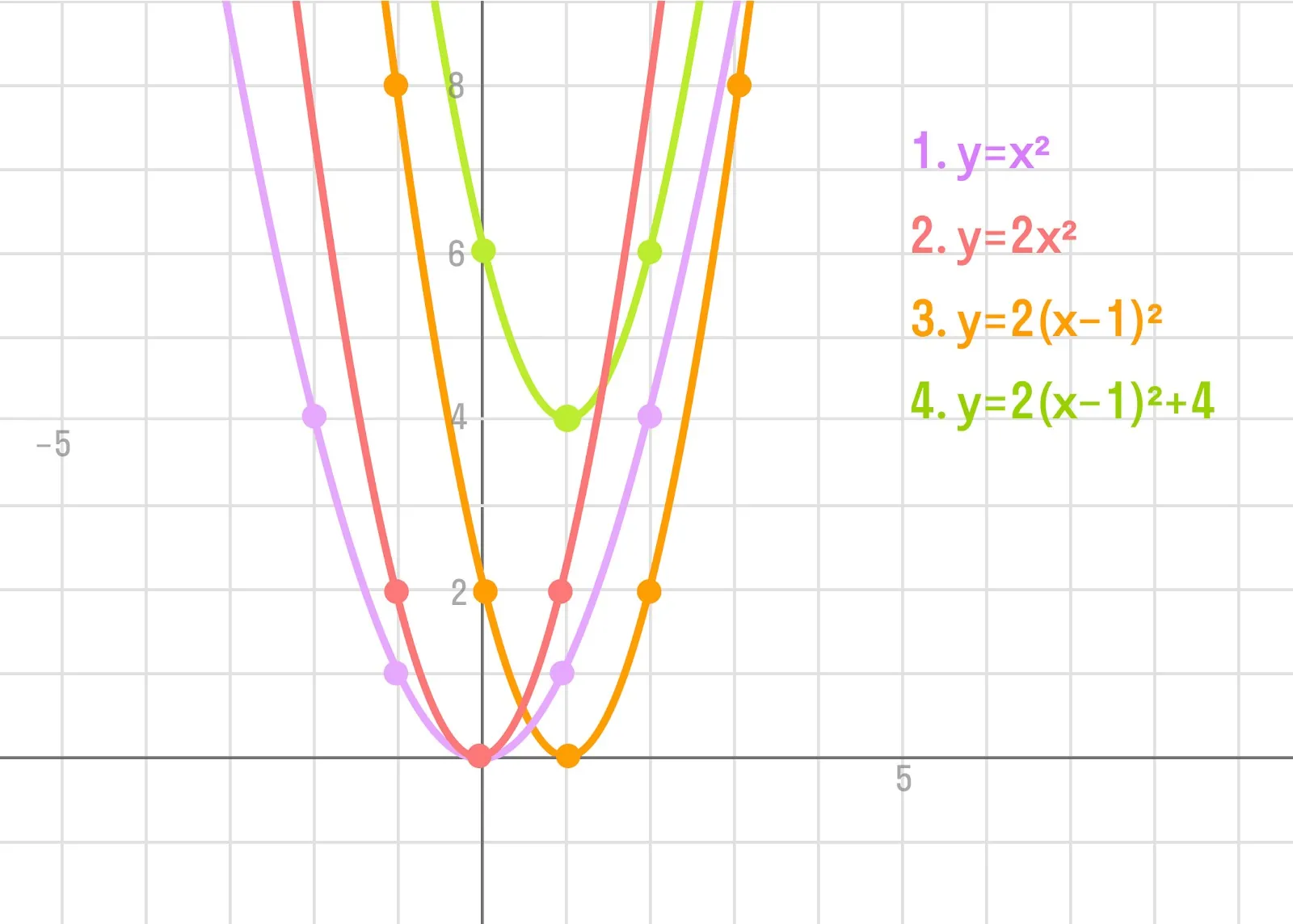
Рассмотрим пример: y = 2 * (x - 1)² + 4.

Как строим:

1. Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:

• построить график функции y = x²,
• умножить ординаты всех точек графика на 2,
• сдвинуть его вдоль оси ОХ на 1 единицу вправо,
• сдвинуть его вдоль оси OY на 4 единицы вверх.

2. Построить график параболы для каждого случая.

   

Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)

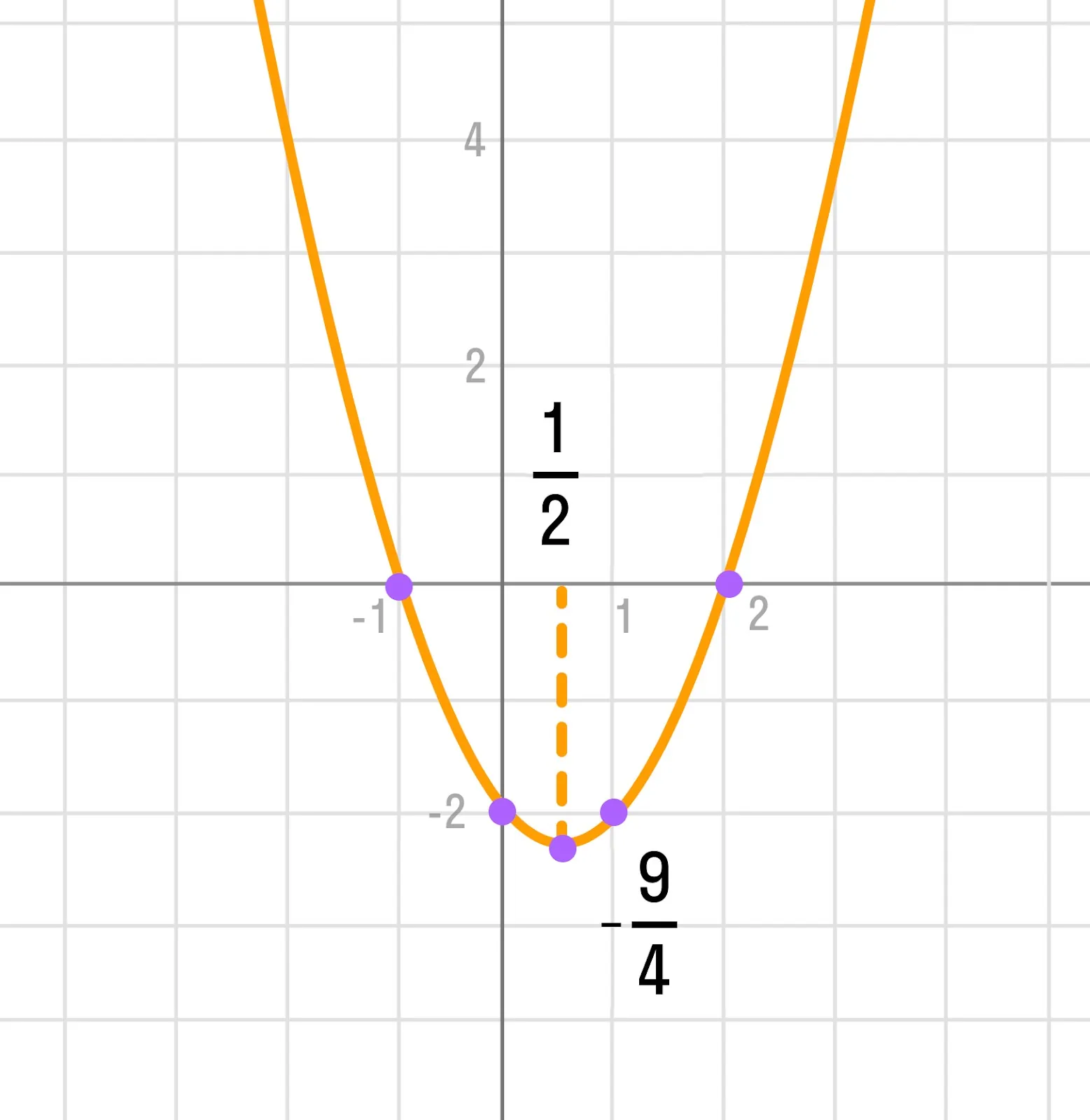
Рассмотрим следующий пример: y = (x − 2) × (x + 1).

Как строим:

1. Данный вид функции позволяет быстро найти нули функции:

   (x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.

2. Определим координаты вершины параболы:

   

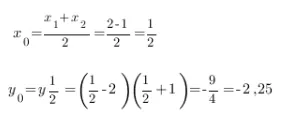
3. Найти точку пересечения с осью OY:

   с = ab = (−2) × (1) = −2 и ей симметричная относительно оси симметрии параболы.

4. Отметим эти точки на координатной плоскости и соединим плавной прямой линией.