Как сокращать алгебраические дроби?

Определение

Алгебраическая дробь — это дробь, в числителе и/или знаменателе которой стоят алгебраические выражения (буквенные множители). Вот так:

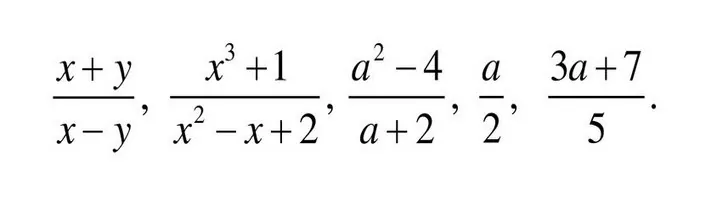
Алгебраическая дробь содержит буквенные множители и степени.

Необыкновенной алгебраическую дробь делают буквы. Если заменить их на цифры, то карета превратится в тыкву — алгебраическая дробь тут же станет обыкновенной.

Если вы засомневались, что должно быть сверху — числитель или знаменатель — переходите по ссылке и освежите знания по теме обыкновенных дробей.

Соглашаюсь на обработку персональных данных в соответствии с условиями пользовательского соглашения

← Далее →

Скачать

Modal window id: popup-professionsbox

Сокращение алгебраических дробей

Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель. Общий множитель числителя и знаменателя в алгебраической дроби — многочлен и одночлен.

Сокращение дробей с буквами и степенями проходит в три этапа:

1. Определите общий множитель.

2. Сократите коэффициенты.

3. Поделите все числители и все знаменатели на общий множитель.

Для сокращения степеней в дробях применяем правило деления степеней с одинаковыми основаниями:

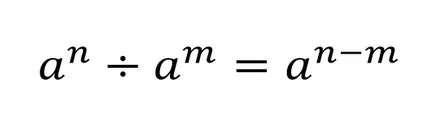
Пример сокращения дроби со степенями и буквами:

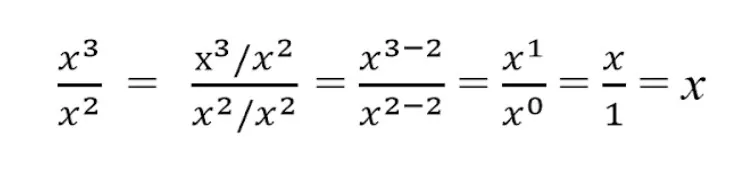
1. Следуя формуле сокращения степеней в дробях, сокращаем x³ и x²

2. Всегда делим на наименьшее значение в степени

3. Вычитаем: 3 - 1

Получаем сокращенную дробь.

Запоминаем: сокращать можно только одинаковые буквенные множители. Иными словами, сокращать можно только дроби с одинаковыми буквами.

❌ Так нельзя	✅ Так можно

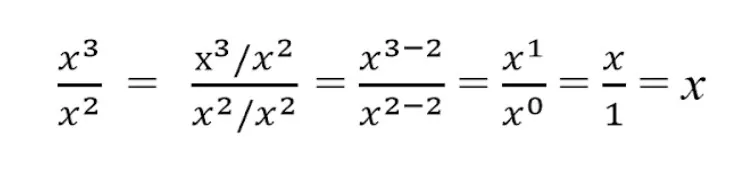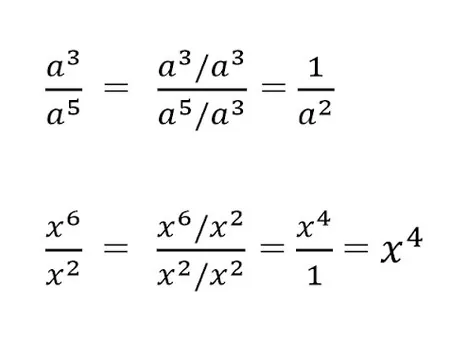Примеры сокращения алгебраических дробей с одночленами:

Пример сокращения №1.

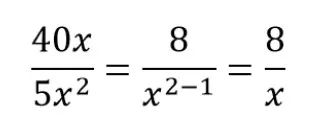
Как решаем:

1. Общий множитель для числителя и знаменателя — 8.

2. Х и x² делим на x и получаем ответ.

Получаем сокращенную алгебраическую дробь.

Пример сокращения №2.

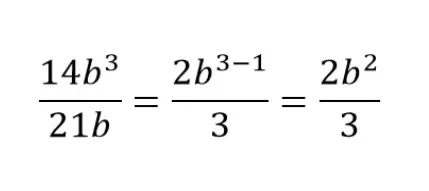
Как решаем:

1. Общий множитель для числителя и знаменателя — 7.

2. b³ и b делим на b.

3. Вычитаем: 3 - 1 и получаем ответ.

Получаем сокращенную дробь.

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

178.1K

Какая профессия тебе подходит? Узнай за 10 минут!

Получи больше пользы от Skysmart:

• Прокачивай знания на курсах математики.

• Выбирай из 1200+ репетиторов по математике.

• Записывайся на бесплатные курсы для детей.

Сокращение алгебраических дробей с многочленами

Чтобы верно сократить алгебраическую дробь с многочленами, придерживайтесь двух главных правил:

• сокращайте многочлен в скобках только с таким же многочленом в скобках;

• сокращайте многочлен в скобках целиком — нельзя сократить одну его часть, а другую оставить. Не делайте из многочленов одночлены.

❌ Так нельзя	✅ Так можно

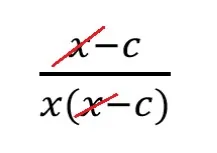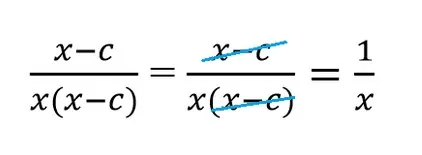Запомните: многочлены в алгебраической дроби находятся в скобках. Между этими скобками вклиниться может только знак умножения. Всем остальным знакам там делать нечего.

Примеры сокращения алгебраических дробей с многочленами:

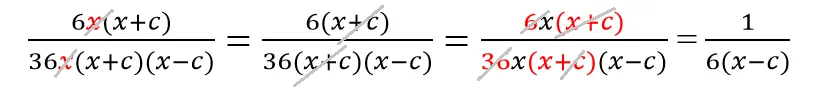
Последовательно сокращаем: сначала x, затем (x+c), далее сокращаем дробь на 6 (общий множитель).

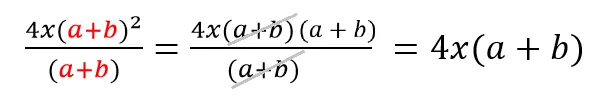
Сокращаем многочлены a+b (в дроби их 3).

Вынесение общего множителя при сокращении дробей

При сокращении алгебраических дробей иногда не хватает одинаковых многочленов. Для того, чтобы они появились, вынесите общий множитель за скобки.

Чтобы легко и непринужденно выносить множитель за скобки, пошагово выполняйте 4 правила:

1. Найдите число, на которое делятся числа каждого одночлена.

2. Найдите повторяющиеся буквенные множители в каждом одночлене.

3. Вынесите найденные буквенные множители за скобку.

4. Далее работаем с многочленом, оставшимся в скобках.

Алгебра не терпит неточность. Всегда проверяйте, верно ли вынесен множитель за скобки — сделать это можно по правилу умножения многочлена на одночлен.

Для умножения одночлена на многочлен нужно умножить поочередно все члены многочлена на этот одночлен.

Пример 1.

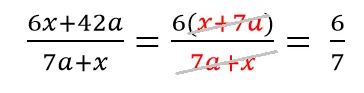
Как решаем:

1. Выносим общий множитель 6

2. Делим 42/6

3. Сокращаем получившиеся одинаковые многочлены.

Пример 2.

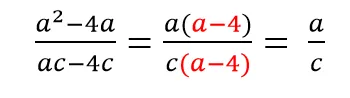
Как решаем: в числителе выносим общий множитель a за скобки, в знаменателе выносим общий множитель c за скобки и сокращаем оставшиеся в скобках многочлены.

Сокращение дробей. Формулы сокращенного умножения

Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.

Чтобы легко ориентироваться в формулах сокращенного умножения, сохраняйте и заучивайте таблицу. Формулы подскажут вам, как решать алгебраические дроби.

Квадрат суммы	(a+b)2 = a2 + 2ab + b2
Квадрат разности	(a-b)2 = a2 - 2ab - b2
Разность квадратов	a2 – b2 = (a – b)(a+b)
Куб суммы	(a+b)3 = a3 + 3a2b + 3ab2 + b3
Куб разности	(a-b)3 = a3 - 3a2b + 3ab2 - b3
Сумма кубов	a3 + b3 = (a + b)(a2- ab+b2)
Разность кубов	a3 - b3 = (a - b)(a2+ ab+b2)

Примеры сокращения дробей с помощью формул сокращенного умножения:

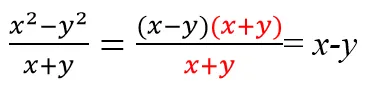
Применяем формулу разности квадратов a² − b² = (a − b) (a + b) и сокращаем одинаковые многочлены.

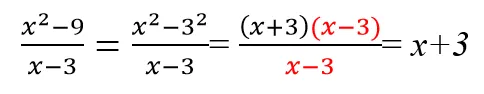
Чтобы раскрыть тему сокращения алгебраических дробей и полностью погрузиться в мир числителей и знаменателей, решите следующие примеры для самопроверки.

Примеры сокращения дробей за 7 и 8 классы

Сократите дроби:

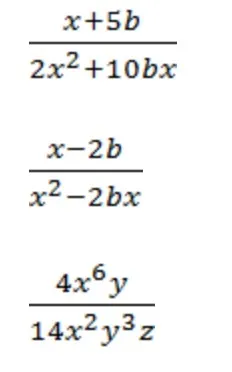
Тема сокращения алгебраических дробей достаточно обширна, и требует к себе особого внимания. Чтобы знания задержалась в голове хотя бы до ЕГЭ, сохраните себе памятку по сокращению дробей. Этот алгоритм поможет не растеряться при встрече с алгебраическими дробями лицом к лицу.

• Чтобы сократить дробь, найдите общий множитель числителя и знаменателя.

• Поделите числитель и знаменатель на общий множитель.

• Чтобы разделить многочлен на множители, вынесите общий множитель за скобку.

• Второй способ разделить многочлен на множители — применить формулы сокращенного умножения.

• Выучите все формулы сокращенного умножения — они помогут легко преобразовывать выражения и экономить время при решении задач.

• Можно забыть свое имя, но формулу разности квадратов помнить обязательно — она будет встречаться чаще других.

• Всегда проверяйте результат сокращения: алгебра — точна, коварна и не любит давать вторые шансы.